| Элементарная теория Бора |   |
Выход из тупика был найден датским ученым Нильсом Бором в 1913 году, получившим Нобелевскую премию в 1922 году.
Бор высказал предположения, которые были названы постулатами Бора. · Первый постулат(постулат стационарных состояний): электроны движутся только по определенным (стационарным) орбитам. При этом, даже двигаясь с ускорением, они не излучают энергию. · Второй постулат(правило частот): излучение и поглощение энергии в виде кванта света (hn) происходит лишь при переходе электрона из одного стационарного состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний, между которыми совершается скачок электрона: Отсюда следует, что изменение энергии атома, связанное с излучением при поглощении фотона, пропорционально частоте ν:
Правило квантования орбит: из всех орбит электрона возможны только те, для которых момент импульса равен целому кратному постоянной Планка:
где n = 1, 2, 3,… – главное квантовое число. Получим выражение для энергии электрона в атоме. Рассмотрим электрон (рис. 6.6,а), движущийся со скоростью
Уравнение движения электрона имеет вид:
Из формулы (6.3.3) видно, что центробежная сила равна кулоновской силе, где Подставим значение υ из (6.3.2) в (6.3.3) и получим выражение для радиусов стационарных орбит (рис.6.6,б):
Радиус первой орбиты водородного атома называют боровским радиусом. При n =1, Z = 1 для водорода имеем: Внутренняя энергия атома слагается из кинетической энергии электрона (ядро неподвижно) и потенциальной энергией взаимодействия электрона с ядром: Из уравнения движения электрона следует, что Подставим сюда выражение для радиуса первой орбиты и получим:
Здесь учтено, что постоянная Планка Для атома водорода при Z = 1 имеем:
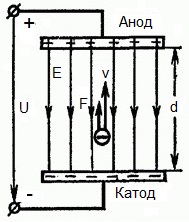
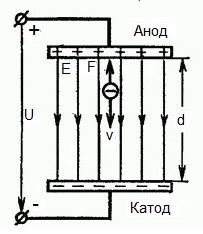
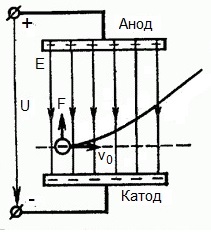
Из формулы (6.3.6) видно, что Схема энергетических уровней, определяемых уравнением (6.3.6) показана на рис. 6.1 и 6.7. При переходе электрона в атоме водорода из состояния n в состояние k излучается фотон с энергией: Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать  Получена обобщенная формула Бальмера, которая хорошо согласуется с экспериментом. Выражение перед скобками, как уже было сказано, носит название постоянной Ридберга: Серьезным успехом теории Бора явилось вычисление постоянной Ридберга для водородоподобных систем и объяснение структуры их линейчатых спектров. Бору удалось объяснить линии спектра ионизованного гелия. Он теоретически вычислил отношение массы протона к массе электрона Однако, наряду с успехами, в теории Бора с самого начала обнаружились существенные недостатки. Главнейшим из них была внутренняя противоречивость теории: механическое соединение классической физики с квантовыми постулатами. Теория не могла объяснить вопрос об интенсивностях спектральных линий. Серьезной неудачей являлась абсолютная невозможность применить теорию для объяснения спектров атома гелия, содержащего два электрона на орбите и тем более для многоэлектронных атомов (рис. 6.8). Стало ясно, что теория Бора является лишь переходным этапом на пути создания более общей и правильной теории. Такой теорией и явилась квантовая механика. Электрон в электрическом полеДвижение электрона в электрическом поле является одним из важнейших для электротехники физических процессов. Разберемся как это происходит в вакууме. Сначала рассмотрим пример движения электрона от катода к аноду в однородном электрическом поле. На приведенном ниже рисунке изображена ситуация, когда электрон покидает отрицательный электрод (катод) с пренебрежимо малой начальной скоростью (стремящейся к нулю), и попадает в однородное электрическое поле, присутствующее между двумя электродами. К электродам приложено постоянное напряжение U, а электрическое поле обладает соответствующей напряженностью E. Расстояние между электродами равно d. В данном случае на электрон со стороны поля будет действовать сила F, пропорциональная заряду электрона и напряженности поля: Поскольку электрон обладает отрицательным зарядом, то эта сила будет направлена против вектора E напряженности поля. Соответственно электрон будет в данном направлении электрическим полем ускоряться. Ускорение a, которое испытывает электрон, пропорционально величине действующей на него силы F и обратно пропорционально массе электрона m. Поскольку поле однородно, ускорение для данной картины можно выразить так: В этой формуле отношение заряда электрона к его массе есть удельный заряд электрона — величина, являющаяся физической константой: Итак, электрон находится в ускоряющем электрическом поле, ибо направление начальной скорости v0 совпадает с направлением силы F со стороны поля, и электрон движется поэтому равноускоренно. Если никаких препятствий нет, то он пройдет путь d между электродами и попадет на анод (положительный электрод) с некой скоростью v. В момент когда электрон достигнет анода, его кинетическая энергия будет соответственно равна: Видео:Уравнение движенияСкачать  Поскольку на всем пути d электрон ускорялся силами электрического поля, то данную кинетическую энергию он приобрел в результате работы, которую совершила сила, действующая со стороны поля. Эта работа равна: Тогда кинетическая энергия, которую приобрел электрон двигаясь в поле, может быть найдена следующим образом: То есть это есть ни что иное, как работа сил поля по ускорению электрона между точками с разностью потенциалов U. В подобных ситуациях для выражения энергии электрона удобно использовать такую единицу измерения как «электронвольт», равную энергии электрона при напряжении в 1 вольт. А поскольку заряд электрона является константой, то и 1 электронвольт — также постоянная величина: Из предыдущей формулы можно легко определить скорость электрона в любой точке на его пути при движении в ускоряющем электрическом поле, зная лишь разность потенциалов которую он прошел ускоряясь: Как мы видим, скорость электрона в ускоряющем поле зависит лишь от разности потенциалов U между конечной и стартовой точками его пути. Представим, что электрон начал движение от катода с пренебрежимо малой скоростью, а напряжение между катодом и анодом равно 400 вольт. В этом случае в момент достижения анода его скорость будет равна: Тут же легко можно определить время, за которое электрон пройдет расстояние d между электродами. При равноускоренном движении из состояния покоя средняя скорость находится как половина конечной скорости, тогда время ускоренного полета в электрическом поле будет равно: Теперь рассмотрим пример когда электрон движется в тормозящем однородном электрическом поле. То есть поле направлено как и прежде, но электрон начинает двигаться наоборот — от анода к катоду. Предположим что электрон покинул анод с какой-то начальной скоростью v и изначально стал двигаться в направлении катода. В этом случае сила F, действующая на электрон со стороны электрического поля, будет направлена против вектора электрической напряженности Е — от катода к аноду. Она станет уменьшать начальную скорость электрона, то есть поле будет замедлять электрон. Значит электрон в данных условиях станет двигаться равномерно равнозамедленно. Ситуация описывается так: «электрон движется в тормозящем электрическом поле». Видео:Физика - уравнения равноускоренного движенияСкачать  От анода электрон начал двигаться с отличной от нуля кинетической энергией, которая при торможении начинает уменьшаться, поскольку энергия теперь расходуется на преодоление силы, действующей со стороны поля навстречу электрону. Если начальная кинетическая энергия электрона, когда он покинул анод, сразу была больше энергии, которую необходимо затратить полю на ускорение электрона при движении от катода к аноду (как в первом примере), то электрон пройдет расстояние d и в итоге все же достигнет катода несмотря на торможение. Если же начальная кинетическая энергия электрона меньше данной критической величины, то электрон не достигнет катода. В определенный момент он остановится, затем начнет равноускоренное движение обратно — к аноду. В итоге поле вернет ему энергию, которая израсходовалась в процессе торможения. А что если электрон влетает на скорости v0 в область действия электрического поля под прямым углом? Очевидно, сила со стороны поля в этой области направлена для электрона от катода к аноду, то есть против вектора напряженности электрического поля E. Значит электрон теперь имеет две составляющие движения: первая — со скоростью v0 перпендикулярно полю, вторая — равноускоренно под действием силы со стороны поля, направленной к аноду. Получается, что влетев в область действия поля, электрон движется по параболической траектории. Но вылетев за пределы области действия поля, электрон продолжит равномерное движение по инерции по прямолинейной траектории. Уравнение движения и уравнение скорости электрона3.1.2 Волновое уравнение. Квантовомеханическое объяснение строения атома Неопределенность установления положения и скорости электрона столь велика, что необходимо вообще отказаться от анализа траектории его движения. Однако есть возможность вероятностного описания строения атома.
m – масса электрона Масса покоя электрона me=9,109 . 10 -31 кг ; E – полная энергия электрона; Видео:Траектория и уравнения движения точки. Задача 1Скачать  x , y , z – координаты. Решением уравнения Шредингера является волновая функция Ψ и соответствующее ей значение энергии электрона E. Вероятность нахождения электрона в пространстве характеризуется квадратом волновой функции, т.е. величиной | Ψ | 2 . Для описания строения атома можно рассматривать электрон как бы “размазанным” в пространстве в виде электронного облака. Величина | Ψ | 2 , полученная из волнового уравнения, является мерой электронной плотности в данном элементе объема, или мерой вероятности нахождения электрона в данном элементе объема атома. Таким образом, в квантовомеханической (вероятностной) модели атома исчезает смысл орбиты, на которой находится электрон. Взамен ее мы имеем дело с электронной плотностью, “размазанной” в пространстве атома. Тело, образованное “размазанным” электроном, называют орбиталью . Обычно под орбиталью понимают часть пространства, заключающую 90% электронного облака. Наличие трех измерений пространства приводит к тому, что в выражении волновой функции Ψ , являющейся решением уравнения Шредингера, появляются три величины, которые могут принимать только дискретные целочисленные значения – три квантовых числа. Они обозначаются символами n , l и ml . Эти квантовые числа характеризуют состояние электрона не только в атоме водорода, но и в любом другом атоме. а) Главное квантовое число ( n ) определяет средний радиус электронного облака, или общую энергию электрона на данном уровне. Оно принимает натуральные значения от 1 до ∞ . В реальных атомах n имеет 7 значений, обозначаемых латинскими буквами K, L, M, N, O, P, Q. Значение n=1 отвечает уровню с самой низкой энергией (т.е. наиболее устойчивому состоянию электрона). Теоретически количество уровней не ограничено, но в атоме главным образом бывают заняты электронами уровни с низкой энергией. б) Побочное, или орбитальное, квантовое число ( l ). В спектрах многоэлектронных атомов наблюдается мультиплетная структура линий, т.е. линии расщеплены на несколько компонент. Мультиплетность линий означает, что энергетические уровни представляют собой совокупности энергетических подуровней, т.к. любой линии в спектре отвечает переход электрона из одного состояния в другое. Энергетические различия в состоянии электронов в данном уровне связаны с различием в форме электронных облаков. Для характеристики энергетических подуровней используется орбитальное квантовое число l . Оно может принимать в пределах каждого уровня целочисленные значения от 0 до n –1. Таким образом, уровень в зависимости от l подразделяется на подуровни, которые имеют также буквенные обозначения: s ( l=0), p ( l=1), d ( l=2), f ( l=3). Электроны, находящиеся в этих состояниях, называются s -, p -, d — и f-электронами. Форма s-электронного облака . Это облако обладает сферической симметрией, т.е. имеет форму шара. График волновой функции Ψ расположен по одну сторону от оси абсцисс (рисунок 3.1), т.е. волновая функция s-электрона положительна. Рисунок 3.1 – График волновой функции s-электрона в зависимости от расстояния до ядра. Форма s-орбитали Форма p-электронного облака . Для p-электрона при удалении от ядра по некоторому направлению волновая функция имеет перегиб (рисунок 3.2). По одну сторону от ядра Ψ положительна , а по другую – отрицательна (не путать знак волновой функции со знаком электрического заряда!). В начале координат Ψ обращается в нуль. В отличие от s-орбитали , p-орбиталь не обладает сферической симметрией, а имеет форму, напоминающую гантель (рисунок 3.2). Рисунок 3.2 – График волновой функции p-электрона. Форма p-электронного облака Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать  Знаки “+” и “–” от носятся не к вероятности нахождения электрона (она всегда положительна и равна | Ψ | 2 ), а к волновой функции, которая в разных частях электронного облака имеет различный знак. Еще более сложную форму имеют электронные облака d — и f-электронов. Например, d-орбитали могут иметь четырехлепестковое строение, причем знаки волновой функции в “лепестках” чередуются: в) Магнитное квантовое число ( ml ). Если атом поместить во внешнее магнитное поле, то происходит дальнейшее расщепление спектральных линий. Это означает, что при данных значениях n и l может существовать несколько состояний электрона с одинаковой энергией. Такие энергетические состояния называются вырожденными. Вырождение исчезает при воздействии на атом внешнего магнитного поля, что и приводит к появлению новых линий в спектре. Энергетические изменения под действием магнитного поля объясняются различием в характере расположения электронных облаков в пространстве и, следовательно, их различной ориентацией по отношению к силовым линиям поля. Магнитное квантовое число ml для данного подуровня – это целочисленная величина в диапазоне от – l до + l . Таким образом, при данном l оно имеет (2 l+1) различных значений. Например, для s-подуровня ( l=0) имеется только одно значение ml , равное нулю. Поэтому s-подуровень содержит единственную орбиталь . Для p-подуровня ( l=1) возможны три значения: ml ∈ . В соответствии с этим каждый p-подуровень состоит из трех орбиталей гантелеобразной формы, ориентированных перпендикулярно друг другу вдоль трех координатных осей и обозначаемых px , py , pz . Легко определить, что на d-подуровне ( l=2) содержится 2 l+1=5 орбиталей , а на f-подуровне ( l=3) – 7 орбиталей . На рисунке 3.3 показано постепенное усложнение представлений о структуре электронной оболочки атома (от уровней к подуровням и далее к орбиталям ). Рисунок 3.3 – Эволюция представлений о строении электронной оболочки атома. Энергетическая диаграмма уровней с 1-го по 3-й г) Спиновое квантовое число ( ms ) не связано с движением электрона вокруг ядра, а определяет его собственное состояние. Природа этого состояния неизвестна до сих пор. Предполагается, что она связана с вращением электрона вокруг собственной оси «Spin» в переводе с английского — «кружение», «верчение». . Число ms принимает два значения: +1/2 и –1/2. Для определения состояния электрона в многоэлектронном атоме важное значение имеет принцип Паули, согласно которому в атоме не может быть двух электронов, у которых все четыре квантовых числа были бы одинаковыми. Следовательно, каждая орбиталь , характеризующаяся определенными значениями n , l и ml , может быть занята не более чем двумя электронами, спины которых имеют противоположные знаки. Такие электроны называются спаренными. Пользуясь принципом Паули, можно подсчитать, какое максимальное число электронов может находиться на каждом подуровне, т.е. определить емкость подуровней: Здесь электроны на орбиталях изображены стрелками, направленными вверх или вниз в зависимости от знака спинового квантового числа. 🔍 ВидеоУравнение для скорости равноускоренного/равнозамедленного движенияСкачать  Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать  Уравнение координат при равноускоренном движенииСкачать  Уравнение скорости при равноускоренном движенииСкачать  Движение электронов в атоме. 1 часть. 8 класс.Скачать  Уравнение равномерного движения. Решение задач по теме.Скачать  Решение графических задач на равномерное движениеСкачать  Уравнение движения РУДСкачать  РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ | скорость движения | УРАВНЕНИЕ ДВИЖЕНИЯСкачать  Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать  Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать  Основные уравнения движенияСкачать  УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать  Урок 106. Реактивное движениеСкачать  РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать  |


 .
. или
или  .
. ,
, в поле атомного ядра с зарядом Ze (при Z = 1 – атом водорода).
в поле атомного ядра с зарядом Ze (при Z = 1 – атом водорода).

 .
. .
. .
. Å = 0,529·10 –10 м.
Å = 0,529·10 –10 м. .
. , т.е. кинетическая энергия равна потенциальной. Тогда можно записать:
, т.е. кинетическая энергия равна потенциальной. Тогда можно записать: .
. .
. , т.е.
, т.е.  .
. .
. принимает только дискретные значения энергии, т.к. n = 1, 2, 3….
принимает только дискретные значения энергии, т.к. n = 1, 2, 3….

 .
. .
. .
. , что находилось в соответствии с экспериментом, является важным подтверждением основных идей, содержащихся в его теории. Теория Бора сыграла огромную роль в создании атомной физики. В период ее развития (1913–1925) были сделаны важные открытия, навсегда вошедшие в сокровищницу мировой науки.
, что находилось в соответствии с экспериментом, является важным подтверждением основных идей, содержащихся в его теории. Теория Бора сыграла огромную роль в создании атомной физики. В период ее развития (1913–1925) были сделаны важные открытия, навсегда вошедшие в сокровищницу мировой науки.

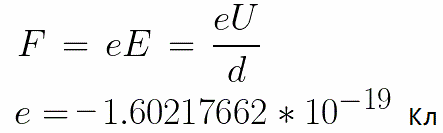
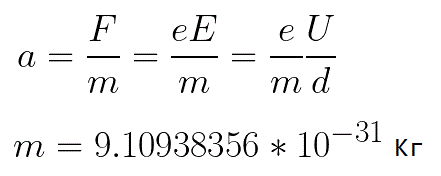
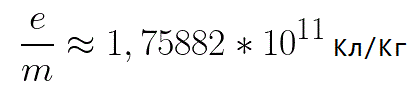
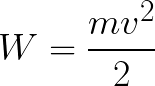
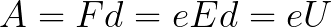
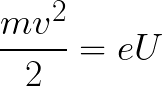
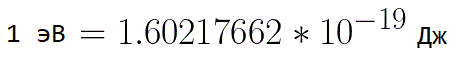
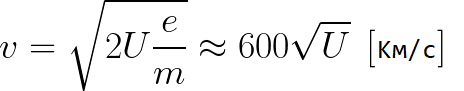
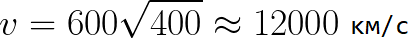
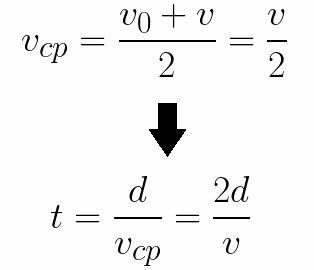
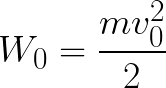
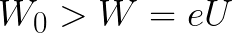
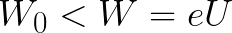
 ,
,



