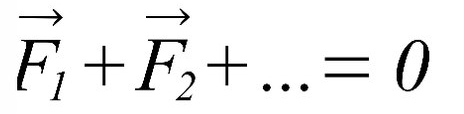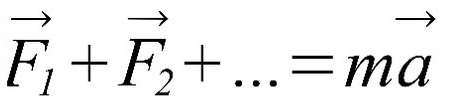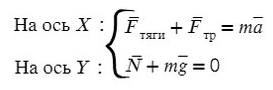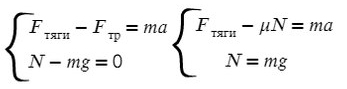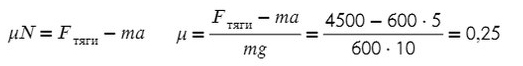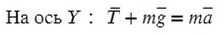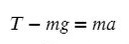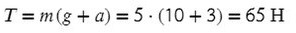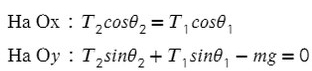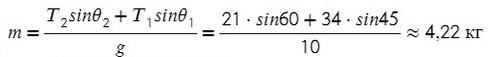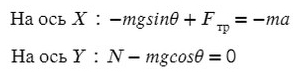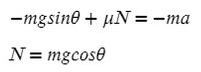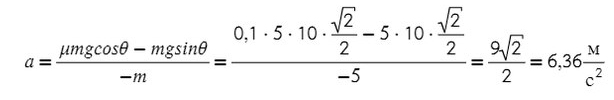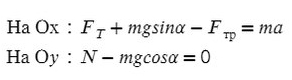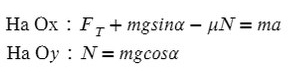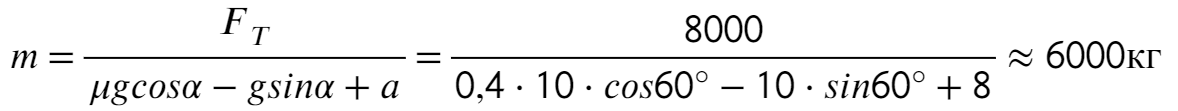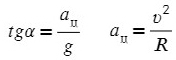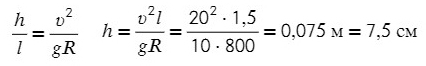Уравнение движения и скорости по оси oy

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Физика

План урока:

Видео:Уравнение движенияСкачать

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.

Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Уравнения движения. Радиус-вектор. Проекция вектора

Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?

Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:

Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.

Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.

В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).

Еще один способ описания движения – векторный.

*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»

Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).

Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r₁ и r₂* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)

Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:

r = r(t)

Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.

Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.

*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.

Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).

Рисунок 4 – Построение проекции вектора на ось

Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, — это и есть искомая проекция.

Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.

Напоминания из геометрии:

два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;

проекции равных векторов равны.

Рассмотрим пример (см. рисунок 5)

Рисунок 5 – Задача на нахождение проекции векторов

Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.

Итак, вектор а: его начала соответствует координате х_н=1, а конец х_к = 4. Значит a_x = х_к – х_н = 4-1 = 3. Вектор b: его начало лежит в точке х_н=2, а конец х_к =0. Значит b_x = х_к – х_н = 0-2 = -2.

В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.

Иногда еще нужно находить составляющие компоненты вектора а_х и а_у. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).

Сумма векторов а_х и а_у равна а. Модули векторов а_х и а_у численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.

Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:

Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины а_х и а_у совпадали бы с координатами тела по осям ОХ и ОY.

Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.

Рисунок 6 – Нахождение компонент вектора а

Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.

Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве

В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.

Точки, в которые попал перпендикуляры к осям – r_x, r_y, r_z – это и есть координаты x, y, z тела в текущий момент времени.

Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.

Рисунок 8 – Построение проекций радиус-вектора

Видео:Физика - уравнения равноускоренного движенияСкачать

Траектория. Путь. Перемещение

Траектория – это линия, вдоль которой движется тело.

Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.

Путь (S), пройденный телом, равен длине траектории.

Перемещение (r)* – это вектор, проведенный из начала пути в конец.

В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.

Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении

*Иногда перемещение так же, как и путь, называют буквой S — (на письме с вектором над ней, при печати — жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.

Видео:Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

• равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r₀, а радиус-вектор в точку Б обозначим r₁. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r₀. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z – это компоненты изначальных векторов r₀ и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х₀) и конечной (х₁) точки на ось ОХ.

Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

Если точка начала двигаться из начала отсчета S₀ = 0, можно переписать эту формулу в виде:

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x₀ = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

Теперь можно записывать уравнение для координаты х:

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x₀ = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Уравнение движения и скорости по оси oy

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

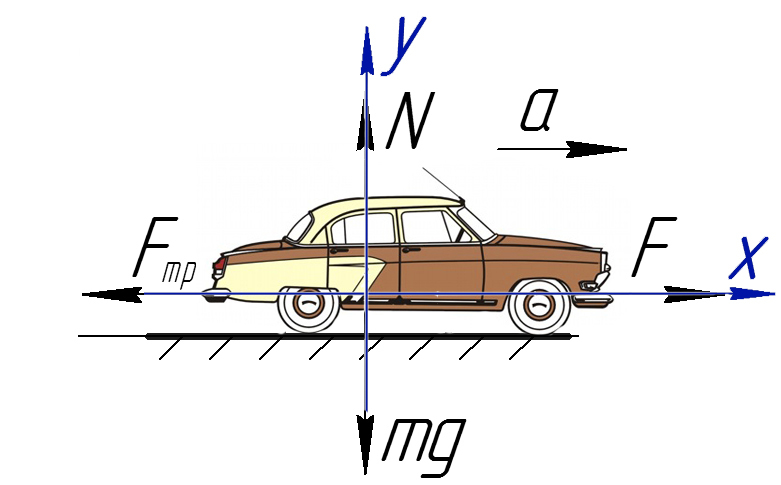
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

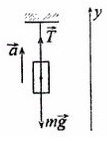
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

T — сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

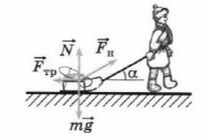
Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

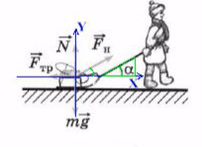
Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

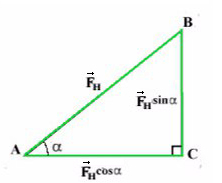
Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

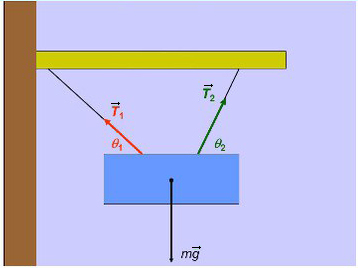
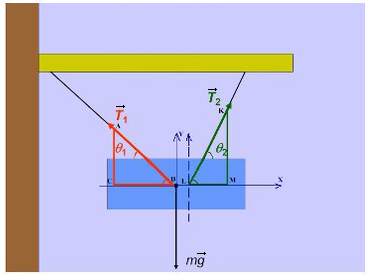
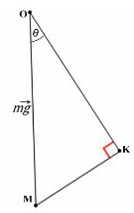
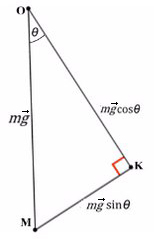
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

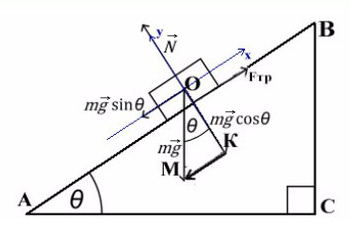
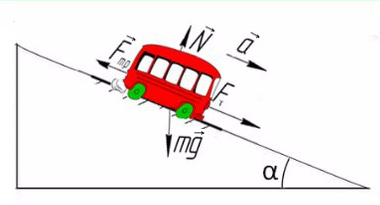
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

Рассмотрим поподробнее ΔKOM:

Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

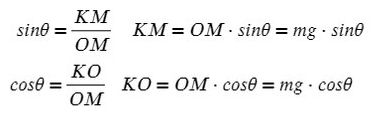
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

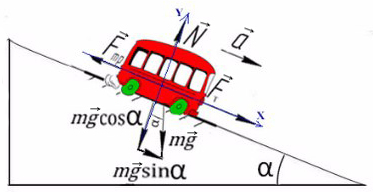
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

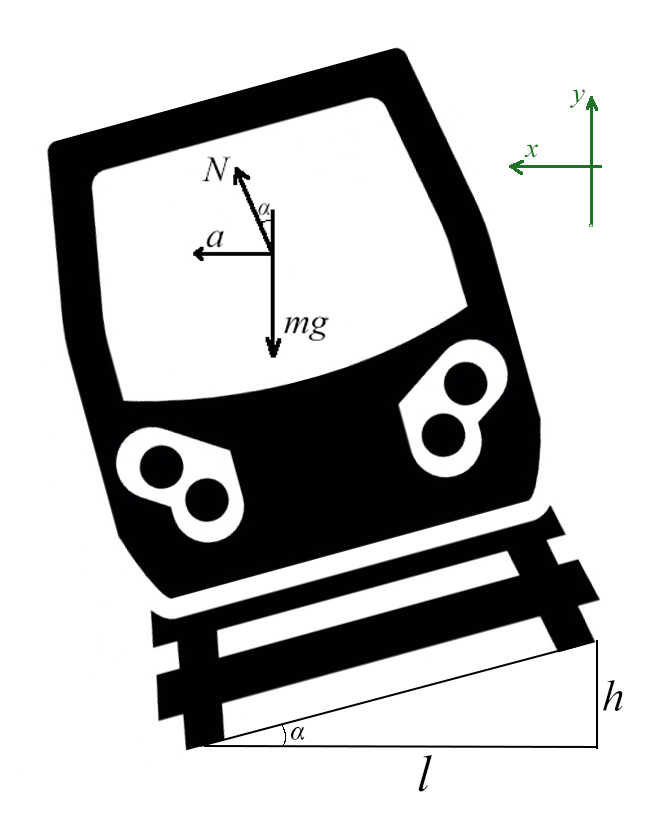
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс — это отношение противолежащего катета к прилежащему:

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.

Видео:Решение графических задач на равномерное движениеСкачать

Скорость и ускорение точки в полярных координатах

Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Скорость и ускорение точки в полярных координатах

• Рассмотрим движение точек на плоскости. В этом случае движение может быть задано в полярных координатах. Для этого возьмите точку O на плоскости в качестве полюса и нарисуйте от нее полярную ось, например, ось быка (рис. 22). Если радиус-вектор r и полярный угол = f2 (t) — (23). Полярный угол считается положительным, если он простирается от полярной оси против часовой стрелки до радиус-вектора. Радиус-вектор как расстояние от точки О до точки М принимает только положительные значения.

Уравнение (23) называется уравнением движения для полярных точек. Это также параметрические точечные траекторные уравнения. Исключение параметра-времени t из (23) дает орбитальное уравнение в полярных координатах. F (r, r = rr °, gr = gfr °. Для проекции скорости на ось, положительное направление которой совпадает с направлением единичного вектора r ° и jr с (24), vr = r, gr = gf. (26) Их называют лучевой и боковой скоростями соответственно. В зависимости от знака производной мицелия лучевая и боковая скорости являются как положительными, так и отрицательными. Используйте (24), чтобы определить ускорение точки в полярных координатах. У нас есть a = dv / dl = (d / d /) (rr 0 + gfr °).

Потенциальная энергия N материальной точки в мыслимой точке силового поля M осуществляется силой поля, действующей на материальную точку при перемещении из точки M в начальную точку Mo, т. Людмила Фирмаль

Проведите дифференциацию и получите a = rf ° + r + r fr 0 + r fr 0 + r f. Для производной по времени единичного вектора p ° dp0 / d ^ = φ (-r0), Вектор p ° вращается с той же угловой скоростью φ, что и вектор r °, поэтому единичным вектором, на который направлен вектор dp ° / dt, является вектор (-r °). Ускоряя производную единичного вектора и подставляя ее в уравнение, объединяющее члены, получаем в = (r-rf2) r ° + (rf + 2rf) p °. (27) Получены точечные ускорения разложения на радиальные ар и боковые ап компоненты. a = a, + ap, ar = (r-rf2) r °, ar = (rf + 2rf) p °. Для проекции ускорений на оси Or и Op получаем a, = r-rp2, ap = rp + 2rp. (28).

Ускорение ar называется радиальным, поперечным направлением. Боковое ускорение также может быть выражено в следующем формате: Эта формула для бокового ускорения широко используется при рассмотрении движения планет и искусственных спутников Земли. Рисунок 23 Равные производные по Поскольку радиальная и боковая составляющие ускорения перпендикулярны друг другу, Для фиксированных координатных осей Ox, Oy и Oz формула ax = dvx / dt, ay = dvy / dt, a2 = dv: / dt. Для подвижных осей Or и Op, как видно из (26) и (28), a и ap не являются временами от vr и vp. Особый случай.

• В этих уравнениях φ — угловая скорость вращения радиус-вектора, а φ — его угловое ускорение. Пример 1. Движение точки — это уравнение r = / (l + COSOH), φ = ШГ, Где я и со постоянные значения. Определить скорость и ускорение точки в полярных координатах траектории уравнения, времени t и момента Решения. Из уравнения движения уберите следующее уравнение для орбиты в полярных координатах: r = f (1 + C0 $ f). Это кардиоидное уравнение (рис. 24).

Проекции скорости и ускорения на полярную ось определяются уравнениями (26) и (28). У нас есть: Мы получаем «, = / = — / Eosin South. 1> = Гф = / ш (1 + COSO) /), t> = + = к ^ 2 (1 + 008 J = ^ 39» 6,2 м / с Прогноз ускорения всегда определяется по формуле а = -2 м / с2; ау = -6 м / с2; а =. > / ai + a * = s / 40×6,3 м / с2, ускорение геля n -2coszsinz + 36-2sin2 (i Ускорение при 2 ^ / 16 cos2 / + 36 sin2 2 / — ^ / 3 / 5® — 0,3 м / с. Далее для r = n / 6 с Скорость предопределена Боковая скорость при =, л / 6 с — по формуле х = 4sin / | Координаты движущейся точки при t = n / 6 на / 6 / 6м. y = 3cos2r | / 6 = 1,5 м. Отметьте положение движущейся точки на траектории в соответствии с координатами, выберите масштаб и нарисуйте векторы скорости и ускорения из проекции на ось.

Таким образом, принцип возможного смещения не является в действительности активной силой, и помимо сил реакции идеального соотношения, для которых задача не определена, определяются все силы энергосистемы. Людмила Фирмаль

Для радиальной составляющей скорости в рассматривается направление, противоположное единичному вектору r °. Это потому, что v был найден со знаком минус. Только числовое значение определяется для боковой составляющей скорости. Из рисунка 25 видно, что направление вектора противоположно направлению единичного вектора p ° (направление p ° получается поворотом вектора r ° на 90 ° против часовой стрелки). Следовательно, в рассматриваемом случае вы должны использовать знак минус для vp, то есть c, = -b, 2 м / с.

Для проверки правильности определения vp вы можете использовать следующую формулу «F. Нормальное ускорение всегда направлено внутрь вогнутой поверхности дорожки. Оказывается, что направление тангенциального ускорения а определяется а и направлено вдоль вектора скорости. В результате точка в определенной точке ускоряется. Определить радиус кривизны орбиты в момент времени t = 1/6 с. Все необходимые для этого количества уже доступны. получить = — = 39/5 «7,8

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🔥 Видео

Урок 12. Равномерное прямолинейное движениеСкачать

РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ | скорость движения | УРАВНЕНИЕ ДВИЖЕНИЯСкачать

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Равномерное прямолинейное движение - физика 9Скачать

Графики зависимости пути и скорости от времениСкачать

Построение проекции вектора на осьСкачать

Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Уравнение равномерного движения. Решение задач по теме.Скачать

Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Используя график скорости, составить уравнение движения тела, имеющего начальную координату -10 м.Скачать