| Название | Минобрнауки россии |
| Анкор | Второй закон Ньютона. Движение под действием постоянной силы. Машина Атвуда.doc |
| Дата | 02.02.2017 |
| Размер | 0.55 Mb. |
| Формат файла |  |
| Имя файла | Второй закон Ньютона. Движение под действием постоянной силы. Ма.doc |
| Тип | Методические указания #1757 |
| страница | 3 из 3 |
| Подборка по базе: Рабочий лист по истории на тему _Национальная и религиозная поли, тест транспорт России. география.docx, Революционный кризис России 1917г..docx, Сценарий поднятия флага России.docx, История государственного управления в России.docx, Отчёт Дети России.docx, Итоговая контрольная работа по русскому языку 1 класс ФГОС Школа, этика второй пакет тестов.docx, Тема №7 Государственные символы России. Символы ратной славы и в, Дни воинской славы и памятные даты России.pptx Содержание Видео:Урок 2. Неподвижные и подвижные блоки. Теория. ЕГЭСкачать  Рисунок 11 Принципиальная схема установки с учётом силы трения и размеров блока и оси блокаМомент силы трения в оси блока M tp = F tp r , где F tp — сила трения между блоком и осью, r— радиус оси. С где μ— коэффициент трения между блоком и осью, зависящий от свойств соприкасающихся поверхностей втулки блока и оси. Таким образом, момент силы трения в оси блока Как видно из (41), значение ε0 не может быть сколь угодно малым. Оно определяется конструкцией блока (например, его радиусами R и r) и коэффициентом трения между блоком и осью. Так как в машине Атвуда m0 -2 10 -1 . На наших установках r/R 10 -4 10 -2 . Мы привели лишь правдоподобные рассуждения о том, каким может быть ε0. Существенно то, что ε0 можно оценить экспериментально. Например, на установке с грузами массой М = 86 г перегрузок массой 1г не страгивает блока, а перегрузок массой 2 г приводит блок в движение. Это значит, что В таком случае оценить ε0, характеризующую установку, можно лишь по порядку величины. Как оказывается, она порядка 10 -2 . Интуитивно ясно, что трением можно пренебречь, если масса перегрузка т m0. Действительно, если масса перегрузка чуть больше m0, то трение в оси блока будет решающим образом определять движение грузов. Это движение уже не будет равноускоренным. Может даже случиться, что система будет двигаться рывками, т. е. остановится, затем снова придет в движение и т. д. Таким образом, при т g. Мы приходим к случаю почти свободного падения. Можно показать, (см. контрольный вопрос 2), что относительная погрешность при определении ускорения грузов, связанная с пренебрежением массой блока и трением, равна Так как величины m0/т и mб /(2М) одного и того же порядка 10 -1 , то и относительная погрешность при измерении ускорения 10 -1 . Очевидно, что такого же порядка будет и относ тельная погрешность при измерении g. 4.14 Методика измерений В первую очередь необходимо определить минимальную массу перегрузка m0 страгивающего блок, с тем, чтобы в дальнейшем проводить измерения с грузами, в 5—10 раз превышающими массу m0. Только в этом случае можно пренебречь влиянием трения на движение системы. Не следует стремиться определить m0 точно, достаточно получить ее правильную оценку «сверху», например, выяснить, что m0 не превышает 1 г или 2 г. Для определения m0 можно постепенно увеличивать массу перегрузка, пока блок придет в движение. Так как блок не может быть отцентрирован идеально, то может оказаться, что в различных начальных положениях блока массы страгивающего перегрузка различны. Поэтому нужно повторить измерения m0, в разных положениях блока, а затем в качестве оценки для m0 взять наибольшее из найденных значений. Следует убедиться, что движение системы при достаточно большой фиксированной массе перегрузка m >>m0 является равноускоренным. Для этого нужно экспериментально проверить выполнение зависимости h = аt 2 /2. Удобно переписать это соотношение в виде из которого ясно, что в осях координат х = Прямая t ( t = где Поэтому было бы грубой ошибкой считать, что погрешность определения времени падения равна 10 -3 с. Для построения графика на оси ординат откладываются измеренные значения где n — число измерений, ti — результат i-гo измерения. На оси абсцисс откладывается Наконец, важно выяснить, подтверждается ли на опыте зависимость времени падения от массы m перегрузка [см. (2)]: В осях координат х = Измерение времени падения при каждом m повторяют несколько раз, результаты усредняют и находят среднее значение 1. Определите массу m0 страгивающего перегрузка. Для этого, постепенно увеличивая массу т перегрузка, определите с точностью до 0,5 г значение m0 , начиная с которого блок приходит в движение. Измерения повторите при четырех положениях блока, каждый раз поворачивая блок примерно на 90° по отношению к предыдущему положению. В качестве m0 следует принять наибольшее из найденных значений. 2. Определите экспериментально зависимость времени падения t груза от высоты h. Измерения проведите при определенном выбранном значении массы перегрузка т = (5 10) m0. При этом необходимо также, чтобы выполнялось неравенство m0 Таблица 1 Зависимость времени падения t от высоты h
Вce значения массы т перегрузка должны лежать в диапазоне Рисунок 12 Примерный вид графика прямой t = t (
7 Контрольные вопросы и задания
8 Литература
Видео:ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать  Уравнение движения грузов если в оси блока есть трениеИзучение законов равноускоренного движения производится на основе анализа кинематических характеристик движения системы тел. Для проведения такого анализа используется машина Атвуда, с помощью которой можно получать различные, не слишком большие (по сравнению с ускорением свободного падения) ускорения. m1 a1=m1 g-T1 (1) | m2 a2=m2 g-T2 (2) | В связи с тем, что нить нерастяжима (x1+x2=l=const), ускорения обоих грузов равны по величине и противоположны по направлению, поэтому уравнение кинематической связи можно записать в виде | a1 = -a2 = a (3) | Из предположений, сделанных ранее, следует также, что натяжения нитей одинаковы, то есть | T1 = T2 = T (4) | Пусть |  , тогда, решая полученную систему уравнений, получаем значение ускорения , тогда, решая полученную систему уравнений, получаем значение ускорения |  (5) (5)и величину силы натяжения нити | |  (6) (6)Ускорение тел системы всегда меньше ускорения свободного падения и меняется при изменении соотношения между массами обоих грузов. | Для выбранной системы тел можно учесть влияние массы блока и силы трения в его оси. Система уравнений в этом случае дополняется уравнением вращательного движения блока и уравнением кинематической связи между угловым ускорением блока и ускорением одного из грузов. Очевидно, что силы натяжения нитей слева и справа от блока будут отличаться. Окончательно система уравнений имеет вид |  (7) (7) |  (8) (8) |  (9) (9) |  (10) (10) |  (11) (11)где J= |  m0R 2 — момент инерции блока, m0 и R — его масса и радиус, m0R 2 — момент инерции блока, m0 и R — его масса и радиус,  -коэффициент, зависящий от распределения массы (от формы блока), -коэффициент, зависящий от распределения массы (от формы блока), 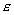 — угловое ускорение блока, Mтр — момент сил трения в оси. — угловое ускорение блока, Mтр — момент сил трения в оси. Решая полученную систему уравнений получаем значение ускорения |  (12) (12)Очевидно, что ненулевые значения силы трения в оси и массы блока уменьшают величину ускорения по сравнению с идеальным случаем. | Проведение эксперимента |  (13) (13)где v1 — скорость груза в момент снятия перегрузка и включения таймера, x1 — координата верхнего фотодатчика. Если в системе отсутствуют силы трения, то с этой же скоростью тело C ‘ будет проходить расстояние между фотодатчиками после снятия с него перегрузка, то есть | |  (14) (14)где L2 = x2 — x1 — расстояние между двумя фотодатчиками (x2 — координата нижнего фотодатчика), t2 — время движения на этом участке пути. | Измерения Устанавливают груз C ‘ в верхнем положении x0 и кладут на него один из перегрузков. Затем устанавливают верхний фотодатчик с закрепленным на нем кронштейном на отметке x1 так, чтобы расстояние между датчиками L2 составляло 15-20 см. В дальнейшем величина L2 не изменяется. Систему тел приводят в движение и определяют время пролета t 2 груза C ‘ между фотодатчиками. Результаты измерений заносят в табл.1. Изменяют координаты начального положения x0 груза C ‘ . Для нового значения L1 проводят измерения в соответствии с п.2. Таблица 1
Обработка результатов Для каждого значения L1 определить значение скорости По результатам измерений строят зависимость v1 2 (L1). Убеждаются, что эта зависимость близка к пропорциональной зависимости, то есть движение груза C ‘ на участке x0 — x1 является равноускоренным и выполняется соотношение (13). С помощью метода наименьших квадратов определяют наклон прямой v1 2 (L1). По наклону прямой находят значение ускорения a и погрешность его определения. Сравнивают полученное значение с найденным по формуле (5). Из уравнений движения (1), (2) при учете (3), (4) следует, что  (15) (15)В процессе выполнения упражнения проводится экспериментальное подтверждение этого соотношения, что свидетельствует о выполнимости второго закона Ньютона | Для экспериментального определения ускорения a можно воспользоваться соотношениями (13) и (14), из них следует, что  (16) (16)Измерения | Установите верхний фотодатчик в среднем положении (по шкале, нанесенной на стойку). Нижний датчик установите так, чтобы расстояние L2 составляло 15-20 сантиметров. Поместите на груз C ‘ один из перегрузков, имеющихся в вашем распоряжении. Определите 3-5 раз время t2 прохождения промежутка L2. Результаты измерений занесите в табл.2. Проведите аналогичные измерения, положив на груз C ‘ два, а затем три перегрузка. Результаты измерений также внесите в табл. 2. Таблица 2
Обработка результатов По экспериментальным данным для каждой из трех величин перегрузков определяется среднее значение времени пролета t2 с использованием формулы Вычислить выборочное стандартное отклонение среднего арифметического значения t2 Используя (16) для каждого Вычислите значения левой Упражнение 3.Оценка влияния силы трения и массы блока на точность результатов. ( Выполняется по указанию преподавателя).  (17) (17)Первый членв разложении полностью совпадает с ускорением (5) для идеальной машины Атвуда, второй и третий также имеют размерность ускорения и определяют систематические погрешности, вносимые силой трения и массой блока |  (18) (18) (19) (19)В этом упражнении требуется на основе использования возможностей экспериментальной установки сделать следующее. | Выработать алгоритмы экспериментального определения величин В соответствии с выбранными алгоритмами провести эксперимент и определить величину либо Что такое инерциальные и неинерциальные системы отсчета? Сформулировать 1-й закон Ньютона. Что такое масса, как ее измерить? Что такое сила, как ее измерить? Сформулировать 2-й закон Ньютона. Сформулировать 3-й закон Ньютона. Сформулировать условия, при которых получены основные соотношения задачи. Как эти условия влияют на вид решаемой системы уравнений. Литература Видео:Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать  Изучение динамики поступательного движения связанной системы тел с учетом силы тренияИзучение динамики поступательного движения связанной системы тел с учетом силы трения Цель работы Оценка роли трения как источника систематической погрешности при определении ускорения на лабораторной установке. Оборудование: установка «машина Атвуда», набор грузов, электронный секундомер. Теоретическое введениеУскорение свободного падения g можно найти с помощью простого опыта: бросить тело с известной высоты h и измерить время падения t, а затем с помощью формулы h = gt2/2 вычислить g. В действительности дело обстоит не так просто, если требуется определить g достаточно точно. Определим время t падения с высоты h = 1,0 м при g = 9,8 м/с2: По нашей оценке при проведении такого эксперимента необходимо измерять время с точностью до 0,01 с. Оценим разброс для t1 = 0,44 c; t2 = 0,45 c; t3 = =0,46 c по формуле g = 2h/t2: Понятно, что измерить время с точностью до 0,01 с не просто. Наручные часы или спортивный секундомер для такой цели непригодны. Если увеличить высоту, то время падения тоже увеличится. Например, с высоты 20 м тело падает около 2 с. В этом случае можно ограничиться меньшей точностью при измерении времени, чем 0,01 с, но возникает ошибка другого характера. Сопротивление воздуха при больших скоростях играет заметную роль. Формула h = gt2/2 описывает равноускоренное движение с ускорением g и, конечно, не учитывает сопротивление воздуха. Таким образом, увеличивая высоту h, мы увеличиваем время падения и уменьшаем относительную погрешность измерения времени, но при этом вносим другую ошибку: сама формула h = gt2/2 становится неточной. Более того, если кирпич сбросить с высоты h » 500 м, то примерно первые 200 м он будет двигаться с ускорением, а затем сила сопротивления воздуха станет равной силе тяжести (это будет при скорости примерно 70 м/с), и тело остальные 300 м будет падать с постоянной скоростью V » 70 м/с. В этом случае формула h = gt2/2 становится неверной. Этот простой пример наглядно подчеркивает общую черту любого физического эксперимента. В любом эксперименте точность измерений какой-либо физической величины связана не только с точностью измерительных приборов, но и с тем, насколько точно принятая модель описывает данный опыт. В рассматриваемом нами опыте мы видим, что точность измерения ускорения g связана не только с точностью измерения времени t , но и с тем, можно или нет пренебречь трением о воздух. Иными словами, достаточно точно или нет, описывает формула h = gt2/2 движение тела. Трудности опыта связаны с большим значением ускорения свободного падения. Так как ускорение большое, то тело быстро набирает скорость, а при этом или время падения мало и его трудно точно измерить, или сама формула Уменьшить ускорение можно с помощью устройства, которое называют машиной Атвуда (рис. 1). которой закреплены грузы массой М каждый. На один из грузов кла- дется перегрузок массой m. Уско – рение грузов легко найти, если а1 Т1 Т2 ввести три предположения (выбрать 1) блок и нить невесомы, т. е. их мас — a2 сы равны нулю (точнее, их массы 2) трением тела о воздух и трением между блоком и его осью можно пренебречь; Рис. 1. 3) растяжением нити можно пренебречь по сравнению с ее длиной. С учетом этих предположений уравнения движения грузов имеют вид: Видео:ФИЗИЧЕСКИЙ ПРАКТИКУМ: МАШИНА АТВУДАСкачать  Mg – T = — Ma(M + m)g – T = (M + m)a где Т = Т1 = Т2 – сила натяжения нити, а = а1 = а2 — ускорение грузов. Из уравнений (1) получаем: При равноускоренном движении без начальной скорости высота h, на которую опускается груз за время t, равна: откуда Формально из выражения (3) следует, что время движения груза может быть сколь угодно большим, если уменьшать e. Например, если взять грузы массами М = 5 кг каждый, перегрузок массой m = 1 г, то e = 10-4, а время спуска груза с высоты h = 1 м примерно равно 45 с. Это время можно достаточно точно измерить секундомером. Однако реально такой опыт неосуществим. Мы предположили, что трение в оси блока отсутствует. Но в действительности оно есть. Весь вопрос в том, можно им пренебречь или нет. Если подвесить к блоку на нитях тяжелые грузы, то в оси блока будет большая сила трения. Чем массивнее грузы, тем больше сила трения. Значит, надо брать достаточно тяжелый перегрузок, чтобы преодолеть эту силу трения и привести всю систему в движение. Сделаем теперь количественные оценки. Пусть mo – масса такого перегрузка, который только-только страгивает блок с грузами. Это значит, что любой перегрузок меньшей массы не приводит систему в движение. В этом случае момент сил натяжения нитей равен моменту силы трения Мтр в оси блока: (T2 – T1 )R = mo gR = Mтр (4) Момент силы трения в оси блока Мтр = Fтрr, где Fтр – сила трения между блоком и осью, r – радиус оси. Сила трения Fтр между блоком и осью пропорциональна силе давления на оси блока. Тогда:
где m — коэффициент трения между Fтр блоком и осью, зависящий от свойств r R соприкасающихся поверхностей втул- ки блока и оси, смазки и т. п. Таким образом, момент силы трения в оси T1 T2 Как видно из (6), значение eо не может быть сколь угодно малым. Оно определяется конструкцией блока (например, его радиусами R и r) и коэффициентом трения между блоком и осью. Так как в машине Атвуда mo > mo. Действительно, если масса перегрузка чуть больше mo, то трение в оси блока будет решающим образом определять движение грузов. Это движение уже не будет равноускоренным. Может даже случиться, что система будет двигаться рывками, т. е. останавливаться, затем снова придет в движение и т. д. Таким образом, при m @ mo, т. е. при e @ eо, формула (2) становится неверной. Можно ожидать, что при e >> eо она достаточно точно описывает реальную ситуацию. Так как eо @ 10-2, то оптимальное значение e 10-1. Это значит, что экспериментировать надо с перегрузками 5 – 20 г (при М = 86 г). Если взять e g. Мы приходим к случаю почти свободного падения. Можно показать (см. контрольный вопрос 2), что относительная погрешность при определении ускорения грузов, связанная с пренебрежением массой блока и трением, равна где mбл – масса блока. Так как величины mo /m и mбл /(2M) одного и того же порядка 10-1, то и относительная погрешность при измерении ускорения Dа/аср 10-1. Очевидно, что такого же порядка будет и относительная погрешность при измерении g. В первую очередь необходимо определить минимальную массу перегрузка mo, страгивающего блок, с тем, чтобы в дальнейшем проводить измерения с грузами, в 5 – 10 раз превышающими по массе mo. Только в этом случае можно пренебречь влиянием трения на движение системы. Не следует стремиться определить mo точно, достаточно получить ее правильную оценку “сверху”, например, выяснить, что mo не превышает 1 г или 2 г. Для определения mo можно постепенно увеличивать массу перегрузка, пока блок не придет в движение. Так как блок не может быть отцентрирован идеально, то может оказаться, что в различных начальных положениях блока массы страгивающего перегрузка различны. Поэтому нужно повторить измерения mo в разных положениях блока, а затем в качестве оценки для mo взять наибольшее из найденных значений. из которого ясно, что в осях координат Прямая где tср – среднее арифметическое значение измеренного времени падения для данной высоты. В условиях эксперимента погрешность Dt оказывается заметно превышающей погрешность в показаниях электронного миллисекундомера (Dt)о, а именно: Dt >> (Dt)о = 10-3 с. Поэтому было бы грубой ошибкой считать, что погрешность определения времени падения равна 10-3 с. Для построения графика на оси ординат откладываются измеренные значения tср с указанием погрешности где n – число измерений, ti – результат i – го измерения. На оси абсцисс откладывается Наконец, важно выяснить, подтверждается ли на опыте зависимость времени падения от массы m перегрузка (см. (2)): В осях координат Измерение времени падения при каждом m повторяют несколько раз, результаты усредняют и находят среднее значение tср и разброс Dt. Полученные экспериментальные данные откладываются на осях координат: на оси ординат – значения tср с указанием погрешности Dt, на оси абсцисс – соответствующие значения 1. Получите у преподавателя набор разновесов. Определите массу mo страгивающего груза. Для этого, постепенно увеличивая массу m перегрузка, определите с точностью до 0,5 г значение mo, начиная с которого блок приходит в движение. Измерения повторите при четырех положениях блока, каждый раз поворачивая блок примерно на 90о по отношению к предыдущему положению. В качестве mo следует принять наибольшее из найденных значений. 2. Определите экспериментально зависимость времени падения t груза от высоты h. Измерения проведите при определенном выбранном значении массы перегрузка m = (5 ¸ 10)mo. При этом необходимо также, чтобы выполнялось неравенство m a=2/k1=0,22 (м/с2) 🌟 ВидеоРешаем задачи на БЛОКИ | ЕГЭ Физика 2023 | ТопскулСкачать  Момент инерцииСкачать  Два тела связанные нитью и неподвижный блокСкачать  Физика.Решение задач.Выполнялка 1Скачать  На вертикальной оси укреплена горизонтальная штанга, по которой могут без трения - №31124Скачать  Урок 82 (осн). БлокиСкачать  Урок 87. Движение по наклонной плоскости (ч.1)Скачать  Блоки. Физика 7 классСкачать  Эта задача с ЕГЭ по Физике отправит тебя в Армию!! Самая сложная задача на блоки!Скачать  Урок 315. Решение задач динамикиСкачать  Урок 93. Основное уравнение динамики вращательного движенияСкачать  Физика. Задача о грузах, подвешенных на блоке.Скачать  Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnlineСкачать  Физика На шнуре, перекинутом через неподвижный блок, подвешены грузы массами 0,3 и 0,2 кг. С какимСкачать  Урок 86. Движение связанных тел (ч.2)Скачать  Как решить любую задачу по механике. АлгоритмСкачать  |
 ила трения Fтр между блоком и осью пропорциональна силе давления на оси блока. Тогда
ила трения Fтр между блоком и осью пропорциональна силе давления на оси блока. Тогда (40)
(40) (41)
(41)
 m0, т. е. при ε
m0, т. е. при ε 10 -2 , то оптимальное значение ε
10 -2 , то оптимальное значение ε

 (42)
(42) , у = t прямая t= t(
, у = t прямая t= t( ,
, — среднее арифметическое значение измеренного времени падения для данной высоты. В условиях эксперимента погрешность t оказывается заметно превышающей погрешность в показаниях электронного миллисекундомера (Dt)0, а именно:
— среднее арифметическое значение измеренного времени падения для данной высоты. В условиях эксперимента погрешность t оказывается заметно превышающей погрешность в показаниях электронного миллисекундомера (Dt)0, а именно: (43)
(43) (44)
(44) , y=t функция t == t (
, y=t функция t == t ( ,
, 

 ±Δg
±Δg при прямолинейном равномерном движении?
при прямолинейном равномерном движении? Экспериментальная установка, получившая название «машина Атвуда», представляет из себя вращающийся с максимально малым трением легкий блок, через который перекинута тонкая нить с грузами массой m1 и m2 (рис.1). На каждый груз действуют две силы — сила тяжести и сила натяжения нити, под действием этих сил грузы и начинают свое движение. Меняя массы грузов можно получать различные ускорения.
Экспериментальная установка, получившая название «машина Атвуда», представляет из себя вращающийся с максимально малым трением легкий блок, через который перекинута тонкая нить с грузами массой m1 и m2 (рис.1). На каждый груз действуют две силы — сила тяжести и сила натяжения нити, под действием этих сил грузы и начинают свое движение. Меняя массы грузов можно получать различные ускорения.  Машина Атвуда состоит из прикрепленной к основанию вертикальной стойки, на которую нанесена шкала (рис.2). На верхнем конце стойки имеется легкий блок, способный вращаться с малым трением. Через блок перекинута легкая нить, к концам которой прикреплены два одинаковых груза C и C ‘ . На груз C ‘ можно помещать добавочные грузы в виде тонких пластин (перегрузки), в результате этого система грузов начинает двигаться с некоторым ускорением. Меняя массу перегрузка, можно менять ускорение системы. После того, как груз C ‘ с перегрузком проходит некоторое расстояние L1 , перегрузок снимается с помощью кронштейна G. После этого грузы начинают двигаться равномерно. На стойке укреплены два фотоэлектрических датчика, соединенные с таймером. При этом верхний фотодатчик соединен с кронштейном G. Фотодатчики могут крепиться на стойке в разных положениях. Система грузов удерживается в состоянии покоя специальной фрикционной муфтой, управляемой с помощью электромагнита.
Машина Атвуда состоит из прикрепленной к основанию вертикальной стойки, на которую нанесена шкала (рис.2). На верхнем конце стойки имеется легкий блок, способный вращаться с малым трением. Через блок перекинута легкая нить, к концам которой прикреплены два одинаковых груза C и C ‘ . На груз C ‘ можно помещать добавочные грузы в виде тонких пластин (перегрузки), в результате этого система грузов начинает двигаться с некоторым ускорением. Меняя массу перегрузка, можно менять ускорение системы. После того, как груз C ‘ с перегрузком проходит некоторое расстояние L1 , перегрузок снимается с помощью кронштейна G. После этого грузы начинают двигаться равномерно. На стойке укреплены два фотоэлектрических датчика, соединенные с таймером. При этом верхний фотодатчик соединен с кронштейном G. Фотодатчики могут крепиться на стойке в разных положениях. Система грузов удерживается в состоянии покоя специальной фрикционной муфтой, управляемой с помощью электромагнита.  где x1 — координата, от которой груз C ‘ начинает свое движение. Учитывая, что при равнопеременном движении скорость меняется по закону v = a t получаем.
где x1 — координата, от которой груз C ‘ начинает свое движение. Учитывая, что при равнопеременном движении скорость меняется по закону v = a t получаем.

 m вычислить значение ускорения a
m вычислить значение ускорения a 

 и правой (B = ai/(g — ai)) частей в соотношении (15) для каждого рассмотренного экспериментального случая. Определить погрешности этих величин. Занести в табл.2 найденные значения. Экспериментально определенные левая и правая части соотношения (15) для трех различных значений
и правой (B = ai/(g — ai)) частей в соотношении (15) для каждого рассмотренного экспериментального случая. Определить погрешности этих величин. Занести в табл.2 найденные значения. Экспериментально определенные левая и правая части соотношения (15) для трех различных значений  и
и  и пренебрегая членами второго порядка малости:
и пренебрегая членами второго порядка малости:

 Через блок перекинута нить, на
Через блок перекинута нить, на (3)
(3) Fтр = mN = m(2M + mo)g
Fтр = mN = m(2M + mo)g Следует убедиться, что движение системы при достаточно большой фиксированной массе перегрузка m >> mo является равноускоренным. Для этого нужно экспериментально проверить выполнение зависимости h = at2/2. Удобно переписать это соотношение в виде
Следует убедиться, что движение системы при достаточно большой фиксированной массе перегрузка m >> mo является равноускоренным. Для этого нужно экспериментально проверить выполнение зависимости h = at2/2. Удобно переписать это соотношение в виде
 , y = t прямая
, y = t прямая  , проходящая через начало координат, соответствует равноускоренному движению.
, проходящая через начало координат, соответствует равноускоренному движению. может быть построена по экспериментальным точкам: для одного перегрузка m и ряда различных значений высоты h измеряется время падения груза. Измерения времени для каждой высоты производятся несколько раз, результаты усредняются и записываются в виде
может быть построена по экспериментальным точкам: для одного перегрузка m и ряда различных значений высоты h измеряется время падения груза. Измерения времени для каждой высоты производятся несколько раз, результаты усредняются и записываются в виде
 . Если полученные экспериментальные точки ложатся на прямую, то движение системы можно считать равноускоренным.
. Если полученные экспериментальные точки ложатся на прямую, то движение системы можно считать равноускоренным. (8)
(8) , y = t функция
, y = t функция  является уравнением прямой. Зависимость
является уравнением прямой. Зависимость  , затем через полученные точки проводится прямая, и по ее наклону определяется значение g.
, затем через полученные точки проводится прямая, и по ее наклону определяется значение g.