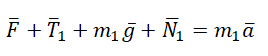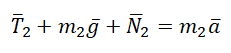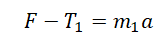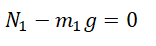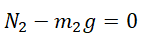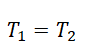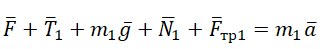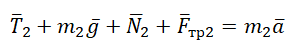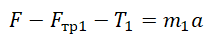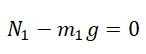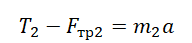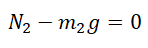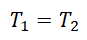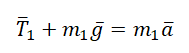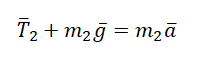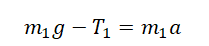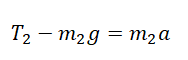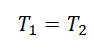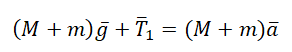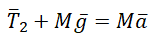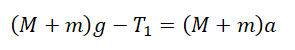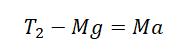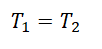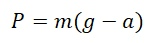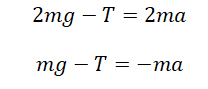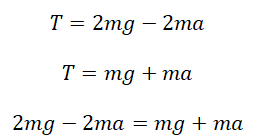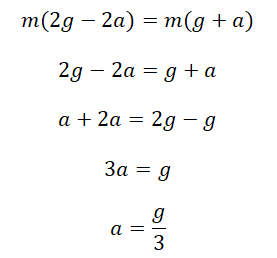Уравнение движения грузов для случая когда массой блока и нити можно пренебречь

[latexpage] Рассмотрим ситуацию, когда в системе тел присутствуют подвижные блоки. Наиболее частое заблуждение у учащихся связано с тем, что подвижный блок дает выигрыш в силе в два раза. Однако при решении задач нужно учитывать тот факт, что выигрыш в силе при использовании подвижного блока или системы блоков равен числу верёвок, на которые опираются подвижные блоки. Наиболее распространенный вариант тот, при котором подвижный блок опирается на две веревки, а значит дает выигрыш в силе в два раза, поэтому сила натяжения нити, которая действует на ось блока будет в два раза больше силы натяжения той нити за которую тянут, чтобы поднять груз. Обратите внимание, что сила натяжения нити перекинутой через блок одинакова в разных точках нити (в данном случае это точки А и В). И сила натяжения нити которая крепится к оси блока и грузу также одинакова во всех точках (в данном случае это точки крепления нити к грузу и оси блока). Но вторая сила натяжения превосходит по модулю первую в два раза.

Заметим также, что точка приложения силы к нити, за которую тянут вверх, проходит путь в два раза больший путь, чем груз, т.е. движется с вдвое большим ускорением, так выигрыш в силе в два раза при использовании подвижного блока приводит к проигрышу в расстоянии в два раза.
Рассмотрим систему состоящая из неподвижного и подвижного блока. Такая система будет давать выигрыш в силе в два раза. Распределение сил и связь ускорений указана на рисунке. Все равенства характеризующие силы натяжения нитей и ускорения следуют непосредственно из пунктов а) и б).

Повторимся, что в рассмотренных случаях каждый подвижный блок опирается на 2 верёвки, значит выигрыш в силе в 2 раза. Если 2 подвижных блока опираются на 4 верёвки получим выигрыш в силе в 4 раза (см. рисунок ниже).

Если подвижный блок опирается на 3 верёвки – выигрыш в силе в 3 раза.

Все три блока связаны одной нитью (выделена синим цветом), поэтому сила натяжения будет одинаковой на всех участках этой нити.

Эту закономерность вообще можно применять для получения любого числа выигрыша в силе. Например, для получения выигрыша в 8 раз надо применить 4 подвижных блока, чтобы они опирались на 8 верёвок. для получения выигрыша в силе в 5 раз необходимо использовать два подвижных блока, опирающихся на 5 нитей.

Задания для самостоятельной работы.

На приведенных ниже рисунках изображены системы блоков. Покажите на рисунках силы натяжения нитей и укажите как связаны их модули.

Для удобства все силы натяжения, одинаковые по модулю, обозначены одним цветом без подписи обозначения сил.

Рассмотрим примеры решения задач, а начнем с немного необычной ситуации.

Пример. Определить ускорения грузов в системе блоков с грузами, изображенной на рисунке. Массой блоков и нитей пренебречь. Нити считать нерастяжимыми.

Решение. Заметим, что все три блока связаны одной и той же нитью, поэтому сила натяжения нити во всех ее точках должна быть одинаковой. Однако, блоки Б и В являются подвижными, в отличии от блока А и должны давать выигрыш в силе в два раза. Теперь перейдем к рисунку и укажем силы натяжения нитей, действующих в системе.

Так как сила натяжения нити одинакова во всех точках, то $T_1=’=T$. Но, с другой стороны, так как блок Б является подвижным, то $T_1=2T$. Равенства $T_1=T$ и $T_1=2T$ будут верными одновременно только в случае если $T=0$. Значит сила натяжения нити в данной системе тел отсутствует, в свою очередь это означает, что на тела действует только сила тяжести и они будут падать свободно, т.е. их ускорение равно $g$.

Пример. В начальный момент времени груз массой $m_1=0,9$ кг в системе блоков, изображенной на рисунке, удерживается. После того, как его отпустили, он проходит путь равный 6 м за 2 секунды. Определить из какого материала изготовлен второй брусок, если известно, что коэффициент трения между бруском и поверхностью стола на котором он находится равен 0,55, а его объем 2 дм 3 . Нить и блоки невесомы, трение в осях блоков и между блоками и нитями нет.

Решение. 1. Систему отсчета свяжем со столом, эта система является инерциальной. Координатную ось $Ox$ направим горизонтально вправо. Координатную ось $Oy$ направим вертикально вниз.

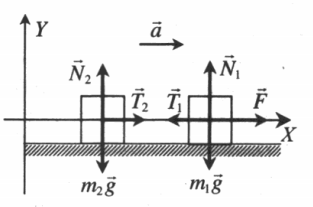
2. Выполним чертеж с указанием всех сил, действующих на тело.

3. Запишем второй закон Ньютона для каждого тела:

$m_2overrightarrow+overrightarrow+<overrightarrow_1>’+overrightarrow_

=m_2 overrightarrow$.

Проекции на координатную ось $Ox$:

Проекции на координатную ось $Oy$:

4. Найдем силу трения, т.к. $N_2=m_2g$, то $F_

=mu N_2=mu m_2g$. Учтем также, что $’=T$, а значит $’=T_1=3T$. Представленная система блоков дает выигрыш в силе в три раза, а значит мы получим проигрыш в расстоянии также в 3 раза, а поэтому, если $a_2=a$, то $a_1=3a$. Запишем полученные в п.3 уравнения с учетом всего вышесказанного

5. Из условия задачи известно, что первое тело, двигаясь из состояния покоя, проходит путь 6 м за 2 с. Запишем формулу для перемещения при прямолинейном равноускоренном движении

6. Вернемся теперь к системе уравнений, полученной в п.4. Выразим из второго уравнения $T$ и подставим в первое

Найдем плотность материала из которого изготовлен второй брусок

Сравнивая табличные значения плотности с найденным, делаем вывод, что брусок — алюминиевый.

В некоторых случаях, приведенные рассуждения бывают не всегда очевидны и могут возникать ошибки при решении задач. Рассмотрим пару примеров.

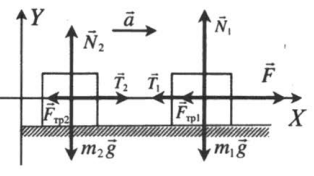
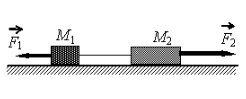
Пример. В системе, изображенной на рисунке, грузы имеют массы $m_1=1$ кг и $m_2=2$ кг. Нить и блоки невесомы, трение в осях блоков отсутствует. Коэффициенты трения грузов о плоскость равны $mu_1=0,5$ и $mu_2=0,3$. В начальный момент времени на верхний блок начинает действовать сила $F=12$ Н, направленная вертикально вверх. На сколько уменьшится расстояние между грузами за 0,4 секунды после начала действия силы $F$? Как изменится ответ, если $F=9$? С каким ускорением будет двигаться ось блока в первом случае?

Решение. 1. Систему отсчета свяжем с поверхностью, относительно которой движутся бруски, эта система отсчета является инерциальной. Координатную ось $Ox$ направим горизонтально вправо. Координатную ось $Oy$ направим вертикально вверх.

2. Выполним чертеж с указанием всех сил, действующих на тело.

3. Запишем второй закон Ньютона для каждого тела:

Проекции на координатную ось $Ox$:

Проекции на координатную ось $Oy$:

4. Найдем силу трения, т.к. $N_1=m_1g$, то $F_=mu_1 N_1=mu_1 m_1g$, соответственно $N_2=m_2g$, то $F_=mu_2 N_2=mu_2 m_2g$. Учтем также, что $T_1=T_2=T$. Так как верхний блок подвижный, то он дает выигрыш в силе в два раза, а значит $T=frac$. И, в заключение, отметим, что ускорения грузов в данном случае будут неодинаковыми, т.к. при равных силах натяжения силы трения будут различными, а значит и равнодействующие также будут различными. Запишем полученные в п.3 уравнения с учетом всего вышесказанного

5. Кинематические уравнения. при движении тела из состояния покоя перемещение тела

6. Из последних двух уравнений найдем ускорения, с которыми движутся тела

Таким образом, второе тело покоится, а первое, двигаясь из состояния покоя, каждое тело пройдет путь равный

Значит, расстояние между телами уменьшится на $s=0,08$ м.

Если же сила $F=9$ Н, то

Значит, оба тела, неподвижны и расстояние между ними не уменьшится.

Для ответа на последний вопрос задачи используем кинематические связи между связанными телами (использовать второй закон Ньютона мы не имеем право, т.к. блок невесом). Так как длина нити не изменяется (нить не растяжима), то получим следующее. Допустим первый груз перемещается на найденное нами расстояние $s$. Блок при этом перемещается вверх. Куда же при этом движется нить? Левая часть вертикального отрезка нити поднимается вверх, а значит любая точка нити пройдет расстояние, которое мы обозначим за $l$. Правая же часть вертикального отрезка нити опускается вниз и также любая точка нити проходит расстояние $l$, потому что ввиду нерастяжимости нити расстояние между двумя обозначенными точками меняться не должно. Тогда общее изменение длины вертикального отрезка нити $2l$ и равно оно $s$. А это означает, что ускорение бруска будет в два раза больше, т.е. ось блока будет двигаться с ускорением $a=0,5$ м/с 2 .

Покажем на примере следующей задачи, как можно использовать кинематические связи при решении задач, попутно дадим образец оформления решения задачи с использованием кинематических связей.

Пример. Через систему блоков, изображенную на рисунке, перекинута нить. К подвижному блоку подвешен груз $M=m_1+m_2$. При каком соотношении масс брусков $m_1$ и $m_2$ бруски не будут скользит друг по другу, если коэффициент трения брусков друг о друга равен $mu$, а коэффициент трения нижнего бруска о плоскость равен нулю? Нить невесома и нерастяжима, трением в блоках и их массой пренебречь.

Решение. 1. Систему отсчета свяжем с поверхностью, относительно которой движутся бруски, эта система отсчета является инерциальной. Координатную ось $Ox$ направим горизонтально вправо. Координатную ось $Oy$ направим вертикально вверх.

2. Выполним чертеж с указанием всех сил, действующих на тело. Заметим заранее, что направления действия сил трения заранее не известны, так как не понятен характер движения тел при их проскальзывании относительно друг друга. Обозначим их на рисунке для порядка как два вектора, направленными противоположно (по третьему закону Ньютона). Так как грузы неподвижны при движении относительно друг друга, то они будут двигаться с одинаковым ускорением.

3. Запишем второй закон Ньютона для каждого тела:

Проекции на координатную ось $Ox$. Так как направления сил трения не известно, то оставим их проекции в полученных уравнениях:

Проекции на координатную ось $Oy$:

4. Учитывая, что оба бруска связаны одной и той же нитью, то $’=T$. Перепишем уравнения для проекций на ос $Ox$, умножим обе части последнего уравнения для груза $M$ на -1 и сложим эти три уравнения, получим

5. Кинематические связи здесь представлены связью уравнений и координат: так как подвижный блок даёт выигрыш в силе в два раза, но не даёт выигрыша в работе, то при смещении бруска каждого бруска на расстояние $x$ груз $M$ смещается на расстояние $y=frac+frac$. Поэтому ускорения брусков и груза связаны уравнением кинематической связи: $2a_1=a+a=2a Rightarrow a_1=a$.

6. Перепишем последнее уравнение и найдем ускорение, с учетом сделанных замечаний

Сумма последних трех уравнений дает нам результат

Учитывая, что векторы сил трения направлены в разные стороны, но одинаковы по модулю $F_+F_=0$, значит

$(m_1+m_2)g=(m_1+m_2)a+(m_1+m_2) Rightarrow a= frac$.

Найдем силу натяжения нити и силу трения

Бруски будут находиться в покое, если модуль силы трения покоя будет больше модуля силы трения скольжения, модуль которой равен $F_=F_=mum_2g$, т.е.

$left | frac right |geqslant mu m_2g$,

$left | frac right |geqslant 4mu$,

$left | 1-frac right |geqslant 4mu.$

Для закрепления пройденного материала и развития навыков задач решения рекомендуется выполнить задания, которые предлагает сайт «Решу ЕГЭ» для подготовки к ЕГЭ по физике на тему «Движение связанных тел» — нажать на ссылку и перейти к решению задач.

Уравнение движения грузов для случая когда массой блока и нити можно пренебречь

2017-05-21
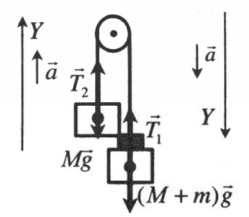
Через блок, прикрепленный к потолку кабины лифта, перекинута нить, к концам которой привязаны грузы $m_ = 0,5 кг$ и $m_ = 0,6 кг$ (рис.). Найти силу давления блока на ось при движении грузов в двух случаях: лифт поднимается равномерно и с ускорением $a_ = 1,2 м/с^$. Масса блока пренебрежимо мала. Трением в оси пренебречь.

Сила давления блока на ось $vec_ = — vec$. где $vec$ — сила реакции оси, действующая на блок и направленная вверх. Кроме этой силы на блок действуют силы натяжения нити $vec_$, и $vec_$, направленные вниз. Уравнение второго закона Ньютона для блока имеет вид

Таким образом, задача сводится к нахождению сил натяжения нити. Поскольку нить связывает заданные грузы, то силы натяжения могут быть найдены из рассмотрения движения грузов. При равномерном движении лифта можно выбрать систему отсчета, связанную как с Землей, так и с лифтом. При ускоренном движении лифта система отсчета, связанная с лифтом, неинерциальная, поэтому она должна быть связана с Землей. Задачу можно решить сразу для ускоренного движения лифта, а первый случай получится как частное решение при $a_ = 0$.

Для доказательства запишем условия нерастяжимости нити. Введем ось $O^ eta$, связанную с лифтом (рис.), координаты обоих тел $eta_$, и $eta_$. Тогда условие нерастяжимости нити

$eta_ + eta_ + l_ = const$,

где $l_$ — длина части нити, соприкасающейся с блоком. При движении грузов относительно лифта координаты $eta_$ и $eta_$ изменяются, но

(точка над буквой обозначает производную по времени); $dot_ = a^_$ — проекция ускорения первого груза относительно лифта на вертикальную ось $O^ eta; ddot_ = a_^$ — проекция ускорения второго груза на ту же вертикальную ось. Из соотношения (1) найдем $a_^ = — a_^$. Поскольку грузы движутся вдоль оси $O^ eta$, то

Относительно Земли ускорения грузов

Каждый из грузов движется под действием силы тяжести и силы натяжения нити. Невесомость нити позволяет считать силу натяжения вдоль нити постоянной по модулю. Неизменяемость силы натяжения по модулю при переходе через блок может быть доказана при условии, что массой блока можно пренебречь. Таким образом, $T_ = T_^ = T_ = T_^$. Уравнения второго закона Ньютона, записанные в скалярном виде для каждого из тел, составят систему, в которой неизвестными будут силы натяжения нити и относительные ускорения грузов.

Коллинеарность сил, действующих на каждый из грузов, позволяет записать уравнения движения сразу в скалярной форме для проекций на ось OY. Для первого груза

для второго груза

Уравнения (2) и (3) образуют систему с двумя неизвестными $T$ и $a^$. Умножая уравнение (2) на $m_$, а уравнение (3) на $m_$ и складывая их почленно, получаем

Искомая сила давления блока на ось

При равномерном движении лифта ($a_ = 0$)

$F_ = 4 m_m_g/(m_ + m_) = 10,7 Н$.

При подъеме с ускорением $a_ = 1,2 м/с^$
$F_ = 4m_m_ (g + a_)/(m_ + m_) = 12,0 Н$.

Движение связанных тел

теория по физике 🧲 динамика

Иногда в системе движется не одно, а два связанных между собой тела. Тогда описание движения с применением законов Ньютона включает в себя описания движения каждого из этих тел.

Движение тел по горизонтали без трения

II закон Ньютона в векторной форме для 1 тела:

II закон Ньютона в векторной форме для 2 тела:

Проекция на ОХ для 1 тела:

Проекция на ОY для 1 тела:

Проекция на ОХ для 2 тела:

Проекция на ОY для 2 тела:

III закон Ньютона:

Движение по горизонтали с учетом сил трения

II закон Ньютона в векторной форме для 1 тела:

II закон Ньютона в векторной форме для 2 тела:

Проекция на ОХ для 1 тела:

Проекция на ОY для 1 тела:

Проекция на ОХ для 2 тела:

Проекция на ОY для 2 тела:

III закон Ньютона:

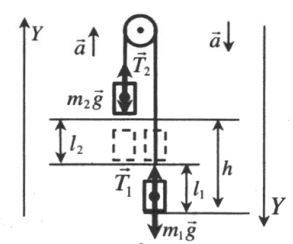
Вертикальное движение тел (m₁ > m₂)

h — расстояние между телами. l₁и l₂— перемещение тела 1 и тела 2 соответственно. Перемещения обоих тел равны, поэтому: l₁ = l₂ = l.

Расстояние между телами определяется формулой: h = l₁ + l₂ = 2l.

II закон Ньютона в векторной форме для 1 тела:

II закон Ньютона в векторной форме для 2 тела:

Проекция на ОY для 1 тела:

Проекция на ОY для 2 тела:

III закон Ньютона:

На один из грузов положили довесок

II закон Ньютона для 1 тела:

II закон Ньютона для 2 тела:

Проекция на ось ОУ для 1 тела:

Проекция на ось ОУ для 2 тела:

III закон Ньютона:

Вес довеска определяется по формуле:

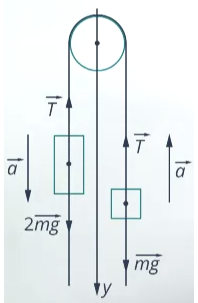
Пример №1. На нити, переброшенной через неподвижный блок, подвешены грузы массами m и 2m. С каким ускорением будут двигаться грузы, если их отпустить? Трением в блоке пренебречь.

Записываем второй закон Ньютона для каждого из тел. Для первого тела он будет иметь

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Для второго тела II закон Ньютона примет следующий вид:

Запишем проекции на ось OУ для каждого из тел:

Выразим силы натяжения нити для каждого из тел и приравняем их правые части:

Сделаем несколько преобразований:

Это значит, если отпустить грузы, они будут двигаться с ускорением, втрое меньшим по сравнению с ускорением свободного падения. Приблизительно оно будет равно 3,33 м/с 2 .

Два груза массами соответственно М₁ = 1 кг и М₂ = 2 кг, лежащие на гладкой горизонтальной поверхности, связаны невесомой и нерастяжимой нитью. На грузы действуют силы F ₁ и F ₂, как показано на рисунке. Сила натяжения нити Т = 15 Н. Каков модуль силы F1, если F2 = 21 Н?

🎬 Видео