Уравнение движения электронов в магнетроне (2 видео)

Содержание

Б)Движение электронов в магнетроне
Движение электронов в магнетроне
Тема: Определение удельного заряда электрона методом магнетрона
🎦 Видео

Видео:Определение удельного заряда электронаСкачать

Б)Движение электронов в магнетроне

Прежде чем рассматривать принцип работы многорезонаторного магнетрона, рассмотрим взаимодействие электрического и магнитного полей на траектории полета электронов между катодом и анодом.

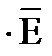
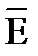
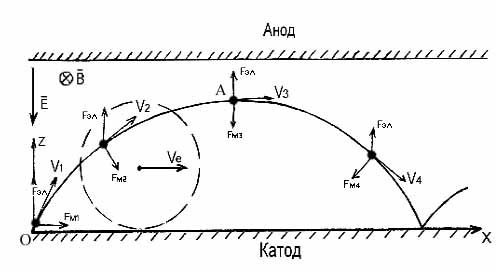
Пусть к электродам магнетрона приложено определенное анодное напряжение, а магнитное поле отсутствует (Н=0). В идеальном случае электроны, испускаемые катодом, будут двигаться по радиусам от катода к аноду под действием электрического поля, Fэ = — e (1) действующей противоположно направлению вектора напряженности электрического поля , т.е. от катода к аноду (рис. 3.22.). В цепи анода будет протекать ток, определяемый током эмиссии катода. При появлении небольшого магнитного поля (Н Hкр) вершины траекторий движения электронов находятся на некотором расстоянии от анода, и анодный ток равен нулю. Именно такой режим и устанавливается в магнетроне.

В качестве примера рассмотрим траекторию движения электронов в плоском диоде в таком режиме (рис. 3.34)

Рис 3.34.Траектория движения электронов в плоском диоде

Магнитное поле с индукцией 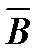направлено в плоскость чертежа перпендикулярно к ней. На всем протяжении движения электрона сила электрического поля Fэ остается постоянной, как по величине, так и по направлению.

В начальный момент, когда скорость электрона еще мала и сила магнитного поля 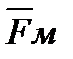, как видно из формулы (2), также незначительна, электрон двигается, главным образом, под действием электрического поля и практически можно считать, что его скорость направлена вдоль оси Oz. С увеличением скорости возрастает сила действия магнитного поля, которая направлена перпендикулярно к вектору скорости и стремится отклонить электрон от прямолинейного движения. Скорость приобретает составляющую, направленную вдоль оси Ох, и траектория движения становится криволинейной. На рис. (рис 3.34) изображены силы, действующие на электрон и направления скоростей для нескольких моментов времени. Из (рис.3.34) видно, что при движении от точки «О» до точки «А», скорость электрона непрерывно возрастает под воздействием силы Fэ, которая на этом участке траектории имеет составляющую, совпадающую с направлением скорости.

После точки «А», когда электрон движется от анода к катоду, скорость его начинает уменьшаться под действием теперь уже тормозящей силы Fэ. На катод электрон возвращается с ничтожно малой скоростью. Траектория, по которой движется электрон в рассматриваемом случае, называется циклоидой.

Из механики известно, что такую кривую описывает точка круга, катящегося без скольжения по плоскости. Радиус круга R и угловую скорость перемещения v можно определить, составив дифференциальное уравнение движения электрона (без вывода):

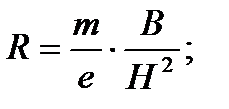
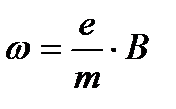
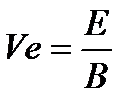
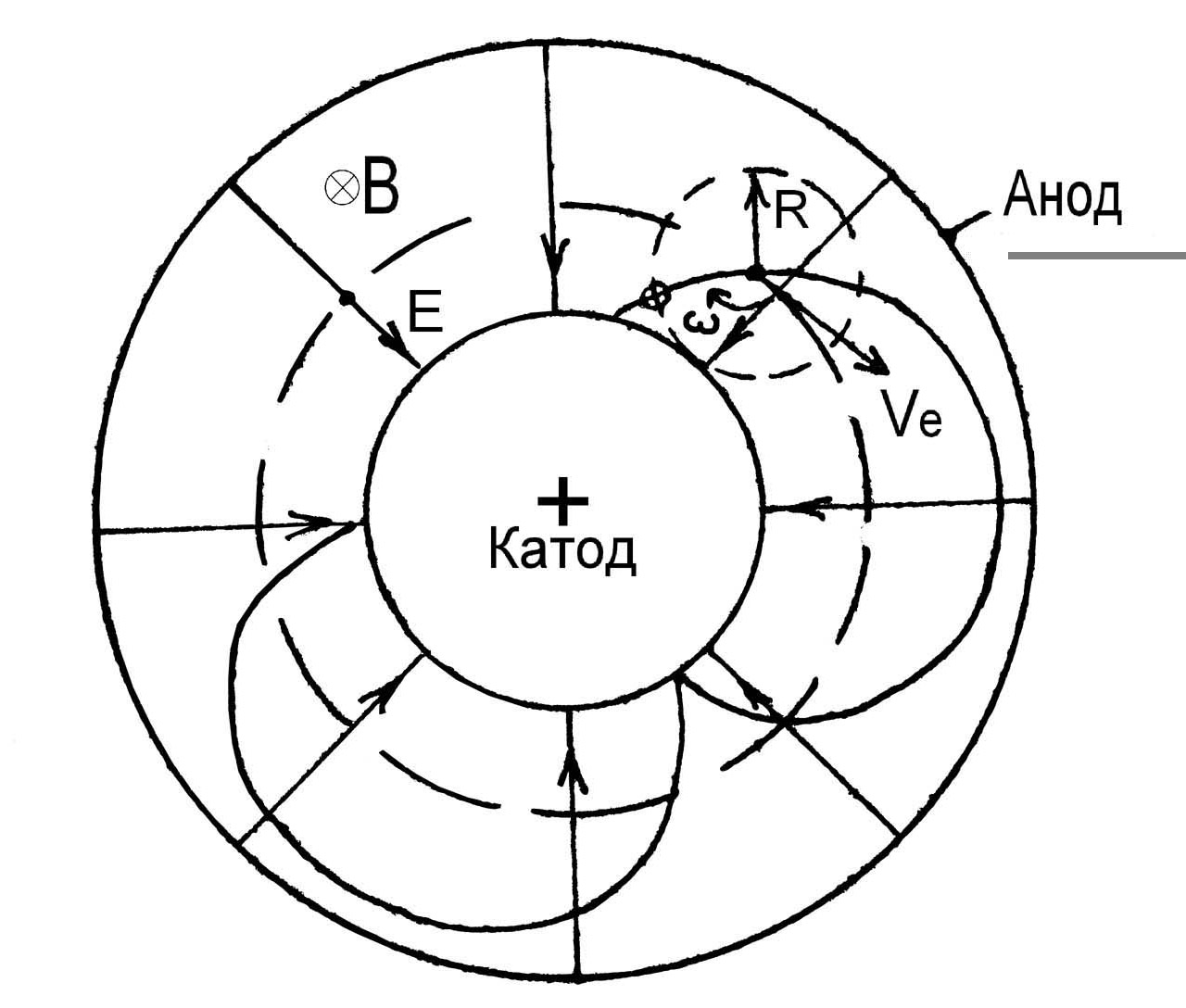
При этом центр круга перемещается со скоростью , которая соответствует средней переносной скорости движения электронов в направлении, параллельном катоду.

В магнетроне катод имеет цилиндрическую форму, поэтому траектория движения электрона будет представлять собой эпициклоиду (рис.3.35.).

Рис.3.35.Траектория движения электрона в магнетроне

Для упрощения мы всегда говорили о движении только одного электрона. В действительности, в магнетронах движется огромное количество электронов, образующих пространственный заряд.

В частности, в цилиндрическом диоде при Н>Hкр электронный поток представляет кольцо пространственного заряда, движущееся вокруг катода с переносной скоростью 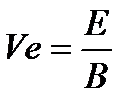. Рассмотрев движение электрона при наличии постоянных электрического и магнитного полей, можно сделать следующие выводы:

1. Величину средней переносной скорости электронного потока, движущегося вокруг катода магнетрона, можно менять, изменяя напряжение на аноде или напряженность магнитного поля;

2. Движущийся электронный поток обладает определенным количеством кинетической энергии 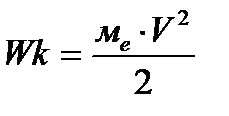, которую он получает от внешнего источника анодного напряжения. При определенных условиях эту энергию можно преобразовать в высокочастотную.

3. Постоянное магнитное поле не изменяет количества энергии электронов, оно влияет на форму траектории электрона и обычно используется для управления электронным потоком.

Видео:Как работает МАГНЕТРОН? Понятное объяснение!Скачать

Движение электронов в магнетроне

ЛАБОРАТОРНАЯ РАБОТА № 46

«ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА»

Заведующий кафедрой ЕНиОТД

профессор, к.т.н. Даутов А.И.

Составил: старший преподаватель

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА

Приборы и принадлежности:

1. Кенотрон типа 2Ц2С на подставке

3. Амперметр на 2 А

4. Миллиамперметр на 150 мА

5. Вольтметр на 300 В

6. Амперметр на 5 А

7. Реостат 10000 Ом

8. Реостат 10 Ом

9. Реостат 100 Ом

10. Реостат 30 Ом

Определение удельного заряда электрона методом магнетрона

Непосредственное измерение массы электрона представляет значительную трудность в виду её малости. Значительно легче определить удельный заряд электрона, т.е. отношение величины заряда к массе e/m, а по величине заряда e и удельное заряду можно найти массу m электрона. Для определения e/m могут применяться различные методы. В данной работе применён так называемый метод магнетрона.

Магнетрон представляет собой двухэлектродную электронную лампу (диск) с цилиндрическим катодом и коаксиальным с ним цилиндрическим анодом. Лампа помещена в однородное магнитное поле, готовые силовые линии индукции которого вектора В направлены параллельно образующим электродов.

Катод нагревает нить накала и испускает (эмитирует) электроны. Если к электродам подключить источник питания («+» к аноду, «-» к катоду), то в промежутке между электродами образуется электрическое поле, линии, напряжённости которого будут направлены по радиусу от анода к катоду. При этом на электроны со стороны электрического поля будет действовать сила:

где е — заряд электрона;

Е — вектор напряженности электрического поля.

Знак «-» показывает, что заряд электрона — отрицательный.

Изменение кинетической энергии электрона при его движении под действием силы может быть найдено по формуле:

, (1)

где φ₁, φ₂ — разность потенциалов начальной и конечной точек пути;

, — начальная и конечная скорости электрона

На электрон, движущийся в магнитном поле, действует сила Лоренца, искривляющая траекторию его движения. Величина и направление силы Лоренца определяется формулой:

, (2)

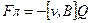
где F_л — вектор силы Лоренца;

— вектор скорости;

В — вектор магнитной индукции.

На рис.2 показано поперечное сечение магнетрона, a и b — радиусы катода и анода соответственно. К электродам приложена разность потенциалов I_а. Магнитное поле направлено перпендикулярно чертежу к читателю. На движущийся электрон в точке С действуют силы и F_л. Сила направлена вдоль радиуса к аноду. Сила F_л, согласно формуле (2), перпендикулярна вектору скорости электрона и вектору индукции магнитного поля В. Направление сил и F_л показано на рис.2. Так как обе силы лежат в плоскости чертежа, движение электрона происходит по плоской спирали переменного радиуса кривизны, зависящего от скорости движения электрона.

Для упрощения задачи будем считать, что начальная скорость электрона у катода .

При В=О на электрон действует сила , движение электрона (с учетом I_а=0) будет прямолинейным вдоль радиуса (рис. 3а). При этом все электроны, эмитируемые катодом, будут достигать анода, создавая анодный ток I_а.

При В>О на электрон, кроме силы , будет действовать сила Лоренца F_л, искривляющая траекторию движения электрона. Если В мала, кривизна траектории будет мала, и все электроны будут достигать анода (рис. 3б).

Зависимость анодного тока магнетрона от величины индукции магнитного поля

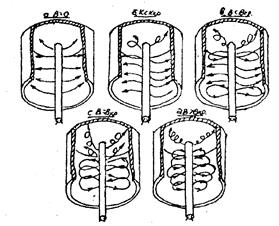
По мере увеличения В траектории будут искривляться все больше и при некотором «критическом» значении В=В_кр траектория электрона окажется касательной к поверхности анода (рис. Зв). При В>В_кр, кривизна траектории станет настолько значительной, что вылетев с катода, электрон будет описывать кривую, заканчивающуюся опять на катоде (рис. 3г). Его скорость в момент возвращения на катод уменьшится до нуля, после чего электрон начнет двигаться к аноду. Поскольку при этом ни один электрон не достигает анода, анодный ток I_а будет равен нулю.

Итак, при В В_кр анодный ток вообще прекратится. При В= В_кр, происходит резкий спад (сброс) анодного тока до нуля (рис. Зв). Зная В_кр, можно найти отношение е/m.

Вывод рабочей формулы для расчёта удельного заряда электрона

Будем считать, что В=В_кр и, следовательно, траектория электрона касательна к поверхности анода (рис.2). Введём полярные координаты: радиус-вектор r (r=OC), и угол поворота радиуса вектора 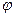относительно вертикального направления ОА.

Вектор скорости электрона можно разложить на составляющую, направленную перпендикулярно к радиусу, и составляющую , направленную вдоль радиуса. Считаем, что при вылете из катода при r=0, .

При r=b траектория электрона касательна к аноду. Следовательно, , для точки касания при r=b можно записать на основании формулы:

, (3)

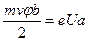
где Ua — разность потенциалов между анодом и катодом.

(4)

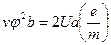
Для определения е/m этого уравнения не достаточно, т.к. неизвестна величина 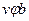. Согласно второму закону динамики для вращательного движения имеем:

(5)

Момент количества движения электрона в любой момент времени равен:

(6)

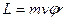
Сила Fе момент не создаёт, т.к. линия её действия проходит через точку О. Поэтому момент силы, действующей на электрон, задаётся только силой Fл (рис.2).

Так как, в нашем случае: F_л=еvВ_кр (см. формулу (2), тогда:

(7)

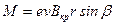
Из рис.3 видно, что , поэтому:

(8)

Произведение можно записать так:

(9)

Тогда из уравнения (5) с учётом (6) и (9) получим:

(10)

Это выражение представляет равенство производных двух функций. Т.к. функции, производные которых равны, могут отличаться лишь аддитивной постоянной, можно записать:

mvφr = 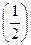еВ_кр r 2 +С (11)

Постоянная С может быть определена из начальных условий. При r=0, vφ=0.

Тогда 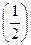еВ_кра 2 +С=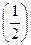0, откуда:

С=- еВ_кра 2 ,

Подставляя значение С в (11), найдём зависимость vφ от радиуса для любой точки траектории:

(12)

При :

(13)

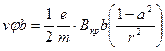
Возводя vφb в квадрат и подставляя в (4), получим:

(14)

Из этого квадратного уравнения можно найти е/m. Так как решение е/m=0 нас не интересует, находим:

(15)

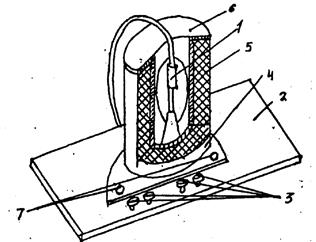
Установка (рис. 4) представляет собой кенотрон типа 2Ц2С 1, укрепленный на специальной подставке 2 с клешами 3, соединёнными с панелью лампы. На лампу надевается соленоид 4, представляющий собой многослойную катушку 5, намотанную на немагнитном каркасе 6, клеммы 7 служат для питания соленоида.

Рис. 4. Вид установки Рис. 5. Принципиальная схема установки

Электрическая схема установки приведена на рис. 5. Она состоит из трех электрических независимых цепей: цепи накала, цепи анода и цепи соленоида. Источником питания двух кенотронных ламп является выпрямитель. Цепь соленоида питается от отдельного селенового выпрямителя. Реостат Rн и амперметр Ан для установки необходимого тока накала. Реостатом Rа и вольтметром Vа поддерживается анодное напряжение. Анодный ток измеряется миллиамперметром mА. Ток в цепи соленоида определяющим величину индукции магнитного поля, устанавливается реостатом Rс 2 по амперметру Ас.

1. Заносят в отчет цену деления и тип каждого прибора.

2. Собирают схему согласно рис. 5.

3. Предъявляют собранную схему преподавателю или лаборанту для проверки.

БЕЗ ПРОВЕРКИ СХЕМЫ ПРЕПОДАВАТЕЛЕМ ИЛИ ЛАБОРАНТОМ ИСТОЧНИКИ ПИТАНИЯ НЕ ПОДКЛЮЧАТЬ!

4. Подключают источник накала (6,3 В) и устанавливают реостатом Rн ток накала 1,75 А.

5. Прогревают катод в течение 2-3 минут, после чего вновь устанавливают ток накала 1,75А. В дальнейшем до окончания измерений реостат накала НЕ ТРОГАТЬ!

6. Включают анодное напряжение (Uа=220 В) и убеждаются в наличии анодного тока по миллиамперметру.

7. Устанавливают максимальное сопротивление реостатом Rс₁ и Rс₂ и включают питание соленоида и включают питание соленоида (Uс=60 В).

8. Устанавливают одно из рекомендуемых анодных напряжений (см. табл. 1).

9. Увеличивая ток соленоида до 1А — через 0,5; от 1А до 4А — через 0,2, записывают в таблицу 1 для каждого значения силы тока соленоида Iс соответствующую силу анодного тока Iа. Установку и отсчет анодного напряжения, силы тока соленоида и анодного тока надо делать очень тщательно, исключая ошибки «на параллакс» и с точностью до десятых долей деления — «на глаз». После каждой установки тока соленоида следует поправлять потенциометром Rа величину анодного напряжения. Необходимо снять 2 сбросовых характеристики при двух разных анодных напряжениях (из числа рекомендуемых).

№ п/п
Ua	Ic
120-200	Ia
№ п/п
Ua	Ic
200-250	Ia

10. Снятые сбросовые характеристики строят в виде графиков обязательно на миллиметровой бумаге.

Рекомендуемое анодное напряжение, Uа=180, 190, 200, 210 В.

Примерный вид сбросовой характеристики показан на рис. 6. По ней можно видеть, что кривая состоит из пяти характерных участков. Такое отличие от рис. 3 объясняются тем, что электроны имеют разброс по тепловым скоростям, так что .

Кроме того, лампа 2Ц 2С, применяемая в работе, имеет форму не цилиндра, а колпачка. Цилиндр с донышком (рис. 7). Поэтому кроме электронов «поперечных», т.е. двигающихся в поперечной плоскости магнетрона, имеются электроны продольные, т.е. двигающиеся параллельно оси или под некоторым углом к ней (рис. 7а).

Рис. 6. Вид сбросовой характеристики Рис. 7

Движение электронов в магнетроне

Разберем явления, соответствующие разным участкам кривой (рис. 6):

1. Ход участка А при В Вкр будут достигать анода лишь продольные электроны, вылетающие с торца. При этом рост поля приводит к росту пространственного заряда вблизи торца (см. пункт 1) и постепенному уменьшению тока (участок F сбросовой характеристики, рис. 7д).

5. Участок D является переходным от участка С к участку F. Существенные роли в расчёте не имеют, поэтому на основании приведённых рассуждений ток на участке D и F, а также переход участка В с участка С и D обусловлены наличием «прохладных» электронов.

Поэтому пересечение продолжений участков В и F (точка О на рис. 6) соответствует прекращению попадания на анод самых «медленных» «поперечных» электронов, т.е. таких, тепловой скорости, которых близки к нулю ( =О). Именно это условие положено в основу при выводе формулы (15). Поэтому I_с будет соответствовать току I_скр для точки О (рис. 7г).

Построение графиков следует, делать очень тщательно, остро отточенными карандашами. Линии должны быть тонкими и плавными. Участки А, В, С, F следует проводить по линейке, а участки переходов — по лекалу или от руки. Все характеристики можно нанести на общий график (желательно разноцветными линиями). Рекомендуемый масштаб по оси ординат — 2 мА в 1 см, по оси абсцисс 0,1-0,2 В в 1 см.

Найдя пересечение участков В и F, опускают перпендикуляр из точки О на ось абсцисс и определяют Iскр.

Критическую индукцию магнитного поля находят по формуле:

Величина коэффициента К указана на соленоиде. Затем по формуле (15) рассчитывают значения е/m и находят их средне-арифметическое значение. Погрешность величины е/m определяется общим методом, исходя из формулы (15), Погрешность значений I_а, I_с, U_а берутся согласно классу точности приборов. Размеры электродов и их погрешность дается ниже. Там же указаны параметры соленоида и их погрешность.

Параметры 2Ц2С: а = (0,095 ± 0,001) см, в = (0,95 ± 0,01) см, К = (0,014 ± 0,001) Тл/а

1. Что такое удельный заряд электрона?

2. Какие методы измерения удельного заряда Вы знаете?

3. Что называется магнетроном? Как он устроен?

4. Какие силы действуют на электрон в процессе движения в магнетроне и как они направлены?

5. Что такое критическое магнитное поле?

6. Какова форма траектории электрона при В В_кр?

7. Расчётная формула определения удельного заряда электрона методом магнетрона?

8. Чем объяснить, несоответствие экспериментальной и теоретической сбросовых характеристик?

9. Каков тип и класс точности электроизмерительных приборов, применяемых в данной работе? Принцип действия приборов?

10. Какие причины (кроме погрешностей измерительных приборов) могут привести к ошибкам в определении ?

Литература

1. Физический практикум. «Электричество и оптика». В.И. Иверова, «Наука», 1968, стр. 321.

2. «Электричество». С.Г. Калашников. «Наука», 1964, § 98, стр. 201-205.

3. Курс физики. Б.М. Яворский и др. «Высшая школа», 1964, т. II, гл. ХVII, § 18.1, 18.8, 18.4, 18.5.

4. Курс общей физики. Г.А.Зисман и О.М. Тодес. М., «Наука», 1965, т. II, гл. VIII, §36, 37.

Видео:ЛР №4. Определение удельного заряда электрона методом магнетронаСкачать

Тема: Определение удельного заряда электрона методом магнетрона

Тема: Определение удельного заряда электрона методом магнетрона.

Цель работы: познакомиться с законами движения заряженных частиц в электрическом и магнитном полях, определить удельный заряд электрона с помощью цилиндрического магнетрона.

Краткие теоретические сведения: магнетроном называется электро-вакуумное устройство, в котором движение электронов происходит во взаимно перпендикулярных электрическом и магнитном полях. Магнетрон является источником электромагнитного излучения СВЧ диапазона.

В нашей работе магнетрон представляет собой радиолампу — диод прямого накала, электродами которой являются коаксиальные цилиндры. Радиолампа помещена во внешнее магнитное поле, создаваемое соленоидом с током (рис.1).

При этом силовые линии электрического поля имеют радиальное направление, а линии магнитной индукции совпадают с осью электродов (рис.2).

Движение электрона в электромагнитном поле подчиняется второму закону Ньютона:

(1)

где r — радиус-вектор, m — масса электрона, e — абсолютная величина заряда электрона, V — скорость электрона, E — вектор напряженности электрического поля, В — вектор индукции магнитного поля.

Траектория движения заряженной частицы в электромагнитном поле существенно зависит от величины удельного заряда — отношения заряда к массе частицы. Уравнение траектории можно получить из решения уравнения (1), но даже в случае цилиндрической симметрии это уравнение не имеет решения в аналитическом виде.

Рассмотрим на качественном уровне движение электрона в цилиндрическом магнетроне. Для упрощения предположим, что электроны вылетают из катода с нулевой начальной скоростью, их движение происходит в плоскости, перпендикулярной оси электродов, а радиус катода много меньше радиуса анода.

При протекании тока в цепи накала, в результате термоэлектронной эмиссии с катода, в лампе образуются свободные электроны. Эмитированные катодом электроны под действием электрического поля движутся к аноду, и в анодной цепи возникает электрический ток. Постоянный ток в обмотке соленоида создает магнитное поле, искривляющее траекторию движения электронов.

Выясним характер движения электронов в магнетроне. В электрическом поле на электрон действует сила F = eE, вынуждающая его двигаться с ускорением в направлении, противоположном вектору Е. Эта сила совершает работу, которая идет на изменение кинетической энергии электрона. Скорость электронов вблизи анода может быть найдена из закона сохранения энергии:

(2)

где Ua — анодное напряжение лампы.

В магнитном поле сила действует на движущийся электрон F=-e[VB] и направлена перпендикулярно скорости электрона. Эта сила не совершает механической работы над электроном, а только изменяет направление вектора скорости и вынуждает электрон двигаться с центростремительным ускорением по окружности. В нашей модели предполагается, что V^B. Применяя второй закон Ньютона, получим:

(3)

Отсюда выразим радиус окружности:

(4)

В магнетроне электрон движется в скрещенных электрическом и магнитном полях. В отсутствии магнитного поля траектории движения электронов приведены на рис. 3а. При наложении “слабого” магнитного поля траектории электронов искривляются, но все электроны долетают до анода, как показано на рис. 3б.

Увеличивая индукцию магнитного поля, можно получить ситуацию, когда электрон, двигаясь по криволинейной траектории, едва не коснется анода и возвратится на катод, как на рис 3в. Криволинейная траектория в этом случае напоминает окружность, радиус которой для электрона вблизи анода приблизительно равен половине радиуса анода

(5)

где значение скорости в соответствии с формулой (2) равно

(6)

Анодный ток при этом прекращается.

Таким образом, если известна индукция критического магнитного поля при определенном анодном напряжении, то из формул (5) и (6) можно рассчитать удельный заряд электрона:

(7)

При дальнейшем увеличении магнитного поля электроны, двигаясь по криволинейным замкнутым траекториям, удаляются от катода на меньшие расстояния и не долетают до анода, как показано на рис. 3г.

Для определения удельного заряда электрона по формуле (7) нужно, задавая величину анодного напряжения, найти значение индукции критического магнитного поля, при котором анодный ток уменьшается до нуля. В данной работе измеряется ток соленоида. Индукция магнитного поля соленоида связана с силой тока соотношением

(8)

где N — число витков, l — длина соленоида. В результате расчетная формула для удельного заряда электрона принимает вид:

(9)

Теоретическая зависимость анодного тока от силы тока в соленоиде для идеального магнетрона приведена на рис.4 (штриховая линия). Здесь же сплошной линией изображена реальная зависимость. Пологий спад анодного тока обусловлен следующими причинами: влиянием краевых эффектов, неоднородностью магнитного поля, некоаксиальностью электродов, падением напряжения вдоль катода, разбросом по скоростям эмитированных электронов и т. д. Разумно предположить, что критическое значение тока соответствует максимальной скорости изменения анодного тока. Для нахождения этой величины нужно построить график зависимости производной анодного тока по току соленоида DIa/DIc от тока соленоида Ic.

Максимум построенной функции соответствует критической силе тока в соленоиде (рис.5).

Описание лабораторной установки: Установка состоит из магнетрона, представляющего собой соленоид с помещенной внутри радиолампой. Конструктивно анод лампы имеет форму цилиндра, вдоль оси которого расположена нить накала, являющаяся катодом. Электрическая схема установки приведена на рис. 6.

Соленоид подключается к источнику постоянного напряжения, а ток соленоида фиксируется амперметром. Справа изображены источник напряжения и приборы, регистрирующие параметры анодной цепи.

Подаем на лампу анодное напряжение 20В. Получили значение анодного тока Іа=0,5834.

Изменяя силу тока в соленоиде, снимаем зависимость анодного тока от тока соленоида. Данные заносим в таблицу:

По данным таблицы построим зависимость анодного тока от тока соленоида.

Графически продифференцируем эту зависимость и определим критическое значение тока соленоида. Максимум построенной функции соответствует критической силе тока в соленоиде.

Таким образом, критическое значение тока соленоида составляет Іс(кр)=320А.

По формуле рассчитаем величину удельного заряда электрона. Взяв длину соленоида 10 см, число витков 1500, радиус анода лампы 5 мм, получаем:

Выводы: в выполненной работе мы познакомились с законами движения заряженных частиц в электрическом и магнитном полях, определили удельный заряд электрона с помощью цилиндрического магнетрона.

1. Что такое магнетрон и как он работает?

Ответ: Магнетроном называется электровакуумное устройство, в котором движение электронов происходит во взаимно перпендикулярных электрическом и магнитном полях. Магнетрон является источником электромагнитного излучения СВЧ диапазона.

В работе магнетрона используется процесс движения электронов при наличии двух полей — магнитного и электрического, перпендикулярных друг другу. Магнетрон представляет собой двухэлектродную лампу или диод, содержащий накаливаемый катод, испускающий электроны, и холодный анод. Магнетрон помещается во внешнее магнитное поле. Анод (анодный блок) магнетрона имеет довольно сложную монолитную конструкцию с системой резонаторов, необходимых для усложнения структуры электрического поля внутри магнетрона. Магнитное поле создается либо катушками с током (электромагнит), либо постоянным магнитом, между полюсами которого помещается магнетрон. Если бы магнитного поля не было, то электроны, вылетающие из катода практически без начальной скорости, двигались бы в электрическом поле вдоль прямых линий, перпендикулярных к катоду, и все попадали бы на анод. При наличии перпендикулярного магнитного поля траектории электронов искривляются силой Лоренца. Траектории движения электронов в магнетроне изображены на рис.1.

Траектория электрона есть циклоида, описываемая точкой, лежащей на окружности круга, равномерно катящегося по катоду. При прохождении циклоидного потока электронов мимо щелей резонаторов анодного блока, в них возбуждаются мощные электромагнитные СВЧ колебания. Высокочастотная энергия из прибора обычно выводится с помощью петли или отверстия связи, помещенных в периферийной части одного из резонаторов анодного блока.

Магнетрон разрабатывался как мощный генератор электромагнитных колебаний СВЧ диапазона для использования в системах РЛС. Эффект нагревания предметов микроволнами нашел применение в микроволновых (СВЧ) печах.

2. Изобразите направление электрического и магнитного полей в магнетроне и траектории движения электронов.

Ответ: В магнетроне электрон движется в скрещенных электрическом и магнитном полях. В отсутствии магнитного поля траектории движения электронов приведены на рис. 3а. При наложении «слабого» магнитного поля траектории электронов искривляются, но все электроны долетают до анода, как показано на рис. 3б.

3. Какие силы действуют на электрон в магнетроне? Укажите направление сил, действующих на электрон в магнетроне. Запишите второй закон Ньютона для электрона в магнетроне.

Ответ: в магнетроне силовые линии электрического поля имеют радиальное направление, а линии магнитной индукции совпадают с осью электродов (рис.2).

Движение электрона в электромагнитном поле подчиняется второму закону Ньютона:

где r — радиус-вектор, m — масса электрона, e — абсолютная величина заряда электрона, V — скорость электрона, E — вектор напряженности электрического поля, В — вектор индукции магнитного поля.

4. Сделайте вывод рабочей формулы.

Ответ: в электрическом поле на электрон действует сила F=eE, вынуждающая его двигаться с ускорением в направлении, противоположном вектору Е. Эта сила совершает работу, которая идет на изменение кинетической энергии электрона. Скорость электронов вблизи анода может быть найдена из закона сохранения энергии:

(1)

где Ua — анодное напряжение лампы. В магнитном поле сила действует на движущийся электрон F=-e[VB] и направлена перпендикулярно скорости электрона. Эта сила не совершает механической работы над электроном, а только изменяет направление вектора скорости и вынуждает электрон двигаться с центростремительным ускорением по окружности. В нашей модели предполагается, что V^B. Применяя второй закон Ньютона, получим:

(2)

Отсюда выразим радиус окружности:

(3)

Увеличивая индукцию магнитного поля, можно получить ситуацию, когда электрон, двигаясь по криволинейной траектории, едва не коснется анода и возвратится на катод. Криволинейная траектория в этом случае напоминает окружность, радиус которой для электрона вблизи анода приблизительно равен половине радиуса анода:

(4)

где значение скорости в соответствии с формулой (1) равно:

(5)

Анодный ток при этом прекращается.

Таким образом, если известна индукция критического магнитного поля при определенном анодном напряжении, то из формул (4) и (5) можно рассчитать удельный заряд электрона

(6)

При дальнейшем увеличении магнитного поля электроны, двигаясь по криволинейным замкнутым траекториям, удаляются от катода на меньшие расстояния и не долетают до анода.

Для определения удельного заряда электрона по формуле (6) нужно, задавая величину анодного напряжения, найти значение индукции критического магнитного поля, при котором анодный ток уменьшается до нуля. В данной работе измеряется ток соленоида. Индукция магнитного поля соленоида связана с силой тока соотношением:

(7)

где N-число витков, l-длина соленоида. В результате расчетная формула для удельного заряда электрона принимает вид:

5. Какие графики нужно построить в данной работе? Поясните ход экспериментальных кривых.

Ответ: в данной лабораторной работе нужно построить график зависимости анодного тока от тока соленоида и график зависимости скорости изменения анодного тока от тока соленоида. Первый график показывает, что при увеличении тока соленоида и соответственно значения вектора магнитной индукции анодный ток прекращается, т. к. радиус движения электронов уменьшается, и они не достигают анода. Второй график позволяет определить ток соленоида, при котором электроны перестают долетать до анода.

1. Савельев общей физики, 1978, т2, §§50,72