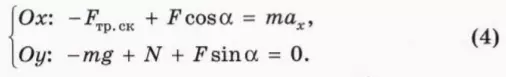Уравнение движения бруска по горизонтали

1. Движение по горизонтали

Сила направлена горизонтально

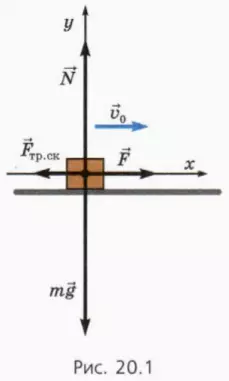
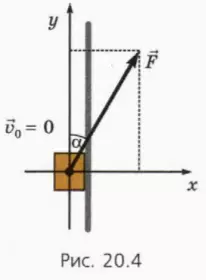
Пусть к бруску массой m, находящемуся на столе, приложена горизонтально направленная сила , а начальная скорость бруска ₀ направлена в ту же сторону, что и сила (рис. 20.1). Коэффициент трения между бруском и поверхностью обозначим μ.

(Здесь и далее будем подразумевать горизонтальный стол.)

(Чтобы выбрать правильное соотношение сил на чертеже, учтите, что значение коэффициента трения заключено обычно в пределах 0,2-0,5. Поэтому модуль силы трения в несколько раз меньше модуля силы нормальной реакции.)

Если тело движется относительно поверхности, с которой оно соприкасается, то на него действует сила трения скольжения.

Направим оси координат, как показано на рисунке 20.1.

1. Объясните, почему справедливо уравнение

2. Объясните, почему из уравнения (1) следует, что:
— при F > μmg скорость тела увеличивается;
— при F

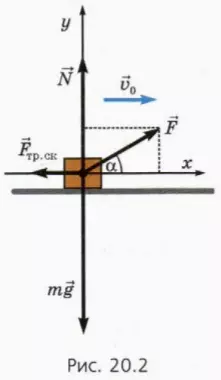
? 7. Используя рисунок 20.2, объясните смысл следующих уравнений:

? 8. К движущемуся по столу бруску массой 0,5 кг приложена сила, равная по модулю 2 Н. Коэффициент трения между бруском и столом равен 0,3. Чему равна проекция ускорения бруска на ось x, направленную по скорости бруска, если сила направлена вверх под углом к горизонту, равным:
а) 30º? б) 70º?

? 9. Чему равны модуль силы нормальной реакции N и модуль силы F при равномерном перемещении по столу бруска массой 2 кг, если коэффициент трения между бруском и столом равен 0,5, а сила направлена:
а) горизонтально?
б) вверх под углом к горизонту, равным 30º?
в) вверх под углом к горизонту, равным 70º?

Итак, когда сила направлена горизонтально, N = mg и F = μmg. Если же направлена вверх под углом к горизонту, то N μmg. (5)

? 11. К покоящемуся бруску массой 2 кг приложена сила, равная по модулю 10 Н. Коэффициент трения между бруском и столом равен 0,5. Чему равно ускорение бруска, если сила направлена вверх под углом к горизонту, равным:
а) 30º? б) 60º?

? 12. Груз массой 10 кг покоится на столе. Коэффициент трения между грузом и столом равен 0,4. Чему будут равны ускорение бруска и действующая на него со стороны стола сила трения, если тянуть брусок силой, равной по модулю 40 Н и направленной вверх под углом 30º к горизонту? под углом 60º к горизонту?

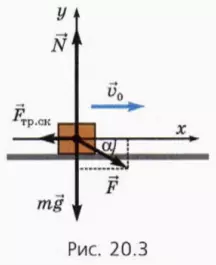
Сила направлена вниз под углом к горизонту

Рассмотрим теперь случаи, когда сила направлена вниз под углом к горизонту, то есть когда брусок не тянут, а толкают.
Пусть начальная скорость бруска равна ₀ (рис. 20.3).

? 13. Объясните, почему в данном случае

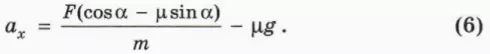
Заметим, что в случае, когда

полученное выражение для проекции ускорения будет отрицательным при любом значении F. Это означает, что при любом значении F скорость бруска будет уменьшаться. Дело в том, что чем больше сила , тем сильнее брусок прижимается к столу – а при этом увеличивается сила трения. И если выполнено неравенство (7), то сила трения растет с увеличением модуля силы быстрее, чем горизонтальная проекция этой силы.

? 14. Груз перемещают равномерно, прикладывая к нему силу 100 Н, направленную вверх под углом 45º к горизонту. Какую силу надо прикладывать, чтобы равномерно перемещать это тело силой, направленной вниз под углом 45º к горизонту? Коэффициент трения равен 0,5.

Рассмотрим теперь случай, когда брусок вначале покоился.

? 15. Объясните, почему брусок не сдвинется с места, если

F(cos α – μ sin α) ≤ mg.

Обратите внимание: в этом случае брусок невозможно сдвинуть с места, как бы велика ни была приложенная сила! В таких случаях говорят, что брусок заклинивает.

? 16. К грузу массой 10 кг, находящемуся на горизонтальной поверхности, прикладывают силу 3 кН, направленную вниз под углом 80º к горизонту. Коэффициент трения равен 0,3. Чему равна действующая на тело сила трения?
Подсказка. Проверьте, заклинит ли груз.

? 17. Груз массой 10 кг покоится на столе. Коэффициент трения между грузом и столом равен 0,2. Чему будут равны ускорение бруска и действующая на него со стороны стола сила трения, если тянуть брусок силой, равной по модулю 40 Н и направленной вниз под углом к горизонту, равным: а) 30º? б) 60º?

2. Движение по вертикали

Пусть брусок массой m прижимают к стене силой , направленной под углом α к вертикали (рис. 20.4). Коэффициент трения между бруском и стеной равен μ.

(Здесь и далее будем подразумевать вертикальную стену.)

Если начальная скорость бруска равна нулю, то есть три возможности: брусок может
— начать двигаться вверх;
— начать двигаться вниз;
— остаться в покое.

Если брусок начнет двигаться, то на него будет действовать сила трения скольжения, а если он останется в покое, то на на него будет действовать сила трения покоя.

? 18. Объясните, почему брусок будет двигаться вверх, если

F(cos α – μ sin α) > mg.

Подсказка. В таком случае на брусок действует сила трения скольжения, направленная вниз.

? 19. Объясните, почему брусок будет двигаться вниз, если

F(cos α + μ sin α) < mg.

? 20. Объясните, почему брусок останется в покое, если выполнены одновременно два неравенства:

F(cos α – μ sin α) ≤ mg и F(cos α + μ sin α) ≥ mg.

? 21.Брусок массой 1 кг прижимают к стене силой, равной по модулю 30 Н. Коэффициент трения между бруском и стеной равен 0,25. Чему равно ускорение бруска и как оно направлено, если сила направлена вверх под углом 30º к вертикали? 70º к вертикали? 80º к вертикали? 90º к вертикали (горизонтально)?
Подсказка. Выясните, начнет ли брусок двигаться. И если начнет, то в каком направлении.

Дополнительные вопросы и задания

22. Чтобы равномерно перемещать груз по столу, можно прикладывать либо силу 12 Н, направленную горизонтально, либо силу 11 Н, направленную вверх под углом 30º к горизонту.
а) Чему равны: коэффициент трения между грузом и столом? масса груза?
б) Чему равна сила нормальной реакции опоры, когда сила направлена вверх под углом 30º к горизонту?

23. Дед Мороз тянет санки массой 10 кг, на которых лежит мешок с подарками массой 20 кг. Веревка, привязанная ‘ к санкам, составляет угол 20º с горизонтом. Коэффициент трения между санками и снегом 0,2. Санки движутся равномерно со скоростью 1 м/с.
а) С какой силой Дед Мороз тянет веревку?
б) С какой силой санки давят на снег?
в) Чему равна действующая на санки сила трения?
г) С каким ускорением будут двигаться санки, если мешок с подарками упадет с ннх, а Дед Мороз будет продолжать тянуть веревку с той же силой?

24. Чтобы равномерно перемещать тело по горизонтальной поверхности, прикладывая силу, направленную вниз под углом 60º к горизонту, надо, чтобы сила была в 14 раз больше силы, направленной вверх под тем же углом к горизонту. Чему равен коэффициент трения?

25. Брусок массой 3 кг прижимают к стене силой 40 Н, направленной под углом 30º к вертикали. В начальный момент брусок покоится.
а) В каком направлении будет двигаться брусок?
б) Чему будет равно ускорение бруска, если коэффициент трения между бруском и стеной равен 0,4? 0,15?

26. С какой наименьшей горизонтальной силой надо прижимать книгу массой 400 г ладонью к стене, чтобы книга покоилась? Коэффициент трения между книгой и стеной равен 0,2, а между книгой и ладонью равен 0,3.
Подсказка. Книга не начнет скользить по стене, пока каждая из сил трения покоя, действующих на книгу (со стороны стены и ладони), не достигнет своего максимально возможного значения.

Видео:Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

Движение по наклонной плоскости тела: скорость, трение, время

Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Видео:Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.

Видео:ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

Здесь v₀ — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

Здесь r — радиус вращения.

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

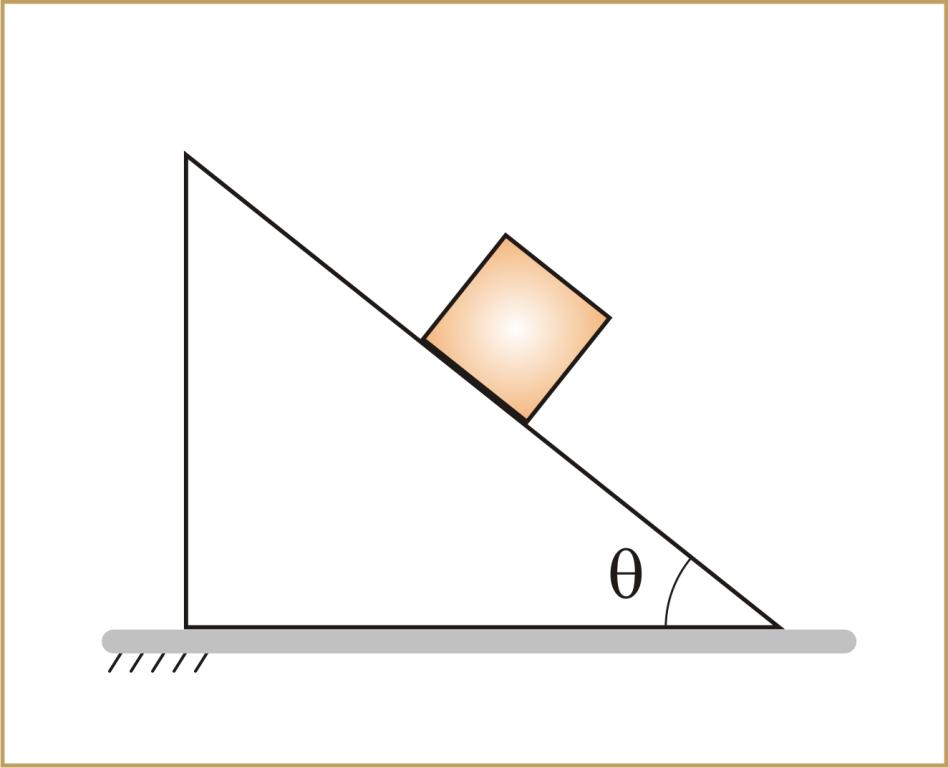
Движение по наклонной плоскости: силы

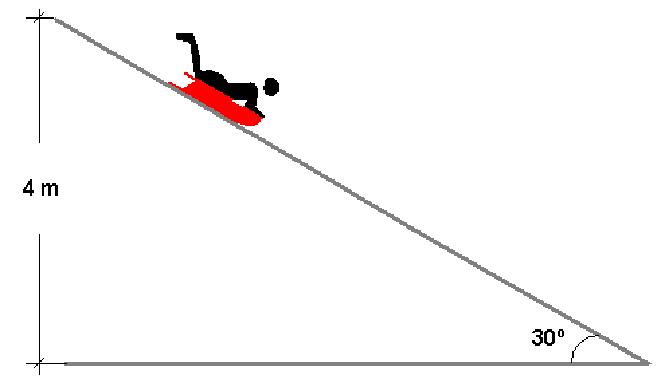
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Видео:Коэффициент тренияСкачать

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Видео:доска и брусокСкачать

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45 o . Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с 2

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

Откуда следует выразить время, и подставить известные значения:

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Видео:Урок 39 (осн). Сила трения. Коэффициент тренияСкачать

Задача со скатывающимся по плоскости цилиндром

Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30 o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

Момент инерции I цилиндра вычисляется по формуле:

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

m*g*sin(φ) — 1/2*m*a = m*a =>

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Видео:Движение тела, брошенного под углом к горизонтуСкачать

Уравнение движения бруска по горизонтали

2018-02-11
Гладкий клин массы $M$ может скользить по горизонтальной плоскости. На его грань, образующую угол $alpha$ с горизонтом, положен гладкий брусок массы $m$. Найти ускорение клина. Трением пренебречь.

Введем горизонтальную и вертикальную составляющие ускорения бруска $a_$ и $a_$. На брусок действуют сила тяжести $m vec$ и сила нормального давления $vec$ со стороны клина. На клин в направлении горизонтали действует лишь горизонтальная составляющая силы нормального давления со стороны бруска $- vec$. Учитывая это, можно записать второй закон Ньютона для горизонтального движения клина н бруска и вертикального движения бруска:

$Ma = N sin alpha, ma_ = N sin alpha, ma_ = mg — N cos alpha$.

Проекции ускорений бруска и клина здесь записаны в системе отсчета, связанной с горизонтальной плоскостью; при этом направление ускорения бруска не совпадает с направлением вдоль наклонной плоскости, так как сама плоскость движется с ускорением $a$. Если перейти в систему отсчета, связанную с клином, то здесь ускорение клина равно нулю, а ускорение бруска будет направлено под углом $alpha$ к горизонту и будет равно по модулю $a_ + a$. На вертикальную проекцию $a_$ переход в новую систему отсчета не окажет влияния. Таким образом, мы можем добавить еще одно необходимое уравнение:

Решая совместно систему четырех уравнений, получаем

Можно предложить и иное решение задачи, воспользовавшись законами сохранения энергии и импульса. Введя горизонтальную $v_$ и вертикальную $v_$ скорости бруска, высоту $h$, с которой он спустился без начальной скорости, и, наконец, скорость клина $u$, из законов сохранения импульса и энергии имеем

Переходя в систему отсчета, связанную с клином (в ней он покоится), с учетом движения бруска в этой системе под углом $alpha$ к горизонту имеем

Если учесть связь между ускорением, путем и скоростью при равноускоренном движении $v_ = sqrt<2 a_р>$ и соотношение между $a_$ и $a$, то приходим, используя всю систему уравнений, к ранее полученному ответу:

📸 Видео

Призма на шероховатом столе (Московкина 15.40)Скачать

Задача "Брусок лежит на бруске. Бруски движутся без проскальзывания"Скачать

ЗАДАЧИ НА НАКЛОННУЮ ПЛОСКОСТЬ - не ГРОБ! КАК ТАКИЕ РЕШАТЬ?Скачать

Урок 4. Движение по горизонтали. Решение задач. ЕГЭСкачать

РЕШЕНИЕ В 3 СТРОЧКИ. Брусок и тележка. Олимпиадная задача по физике. Часть 2. #shortsСкачать

подвижный клин наклонная плоскостьСкачать

#5 Задача по физике (динамика)Скачать

Урок 106. Реактивное движениеСкачать

На горизонтальной шероховатой поверхности стола лежит брусок массой 500 г. К бруску - №26401Скачать

На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения - №22748Скачать

Скольжение бруска по движущемуся клину | Физика ЕГЭ, динамика | 10, 11 классСкачать

Выполнялка 184. Механика. Коробку равномерно тянутСкачать