Уравнение движения автомобиля в общем виде

Видео:Физика - уравнения равноускоренного движенияСкачать

Уравнение движения автомобиля

Уравнение движения автомобиля выражает связь между движущими силами и силами сопротивления движению и позволяет определить режим движения автомобиля в любой момент.

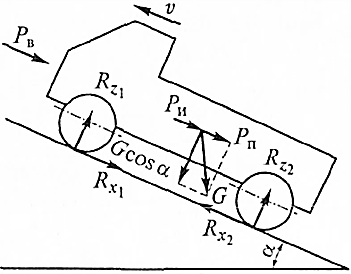
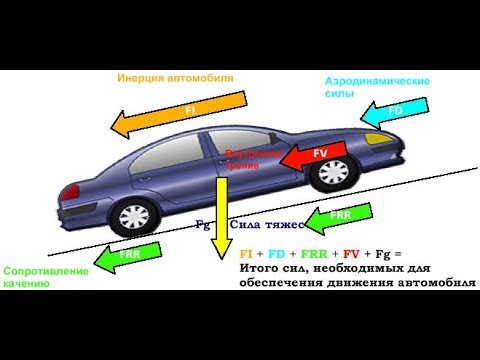
Для вывода уравнения движения используется схема движения автомобиля на подъем и рассматривается разгон автомобиля на подъеме (рис. 4.1).

Рисунок 4.1 – Схема сил, действующих на автомобиль на подъеме

Проекция всех сил, действующие на автомобиль на поверхность дороги:

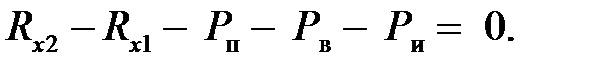(4.1)

Подставим в формулу (4.1) касательные реакции дороги R_х1 и R_х2, объединим члены с коэффициентом сопротивления качению f и члены с ускорением j и, принимая во внимание соотношения f (R_zl + R_z2) = P_к. При этом учтем, что j_k1 + j_k2 = j_k ,а также принимая во внимание коэффициент учета вращающихся масс, получим уравнение движения автомобиля в общем виде: .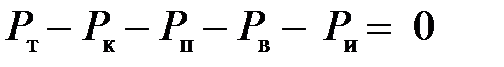

Принимая во внимание, что силы сопротивления качению Р_к и подъему Р_п в совокупности представляют силу сопротивления дороги Р_д, получим:

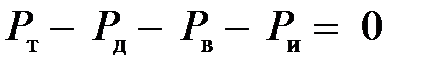(4.2)

При установившемся (равномерном) движении, когда нет разгона и Р_и = 0:

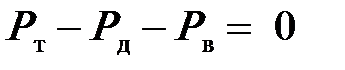(4.3)

Из уравнения (4.3) следует, что безостановочное движение автомобиля возможно только при условии:

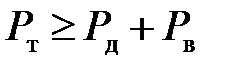(4.4)

Данное неравенство связывает конструктивные параметры автомобиля с эксплуатационными факторами, обусловливающими сопротивление движению, и не гарантирует отсутствия буксования ведущих колес. Безостановочное движение автомобиля без буксования ведущих колес возможно лишь при соблюдении условия:

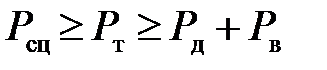(4.5)

Условие равномерного движения при отсутствии буксования ведущих колес записывается в виде:

Видео:Уравнение движенияСкачать

Устройство автомобилей

Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Уравнение движения автомобиля

Силовой баланс при прямолинейном движении автомобиля

В предыдущей статье рассмотрены все силы, действующие на автомобиль во время его прямолинейного движения – сила тяги Р_т , сила тяжести G , сила сопротивления воздуха Р_ω , касательные R_x и нормальные R_y составляющие реакции дороги, силы инерции P_j , силы сопротивления подъему P_α , силы сопротивления качению колес P_f , и (в случае движения автопоезда) сила Р_пр на буксирном крюке.
Эти силы можно разделить на две группы – силы, обеспечивающие движение автомобиля, и силы сопротивления, препятствующие этому движению. В общем случае лишь одна сила обеспечивает его движение – сила тяги Р_т , приложенная к ведущим колесам. В частных случаях реально помогать движению автомобиля могут еще три силы – сила тяжести (при движении под уклон), сила инерции и сила попутного ветра. Тем не менее, эти силы при составлении динамического баланса тоже следует отнести к силам сопротивления движению автомобиля, учитывая лишь их векторное значение для каждого конкретного случая..

Спроектировав все силы на плоскость опорной поверхности автомобиля, получим уравнение динамики прямолинейного движения:

Очевидно, что движение возможно лишь в том случае, если сила тяги Р_т будет больше суммы сил P_ψ , P_j , P_ω , препятствующих движению. При этом движение возможно до тех пор, пока не начнется пробуксовка ведущих колес, т. е. сила тяги на ведущих колесах не превысит значение, при котором не будет иметь место сцепление шин с поверхностью дороги.

Сила тяги по сцеплению

Сила тяги образуется касательными реакциями дороги. Эти реакции представляют собой силы трения и силы зацепления, при этом силы зацепления возникают на деформируемых грунтах. Сила тяги ведущего колеса, которую можно реализовать для движения автомобиля на данном дорожном покрытии или грунте, имеет предел, зависящий от сцепных свойств шины.

Предельные значения силы тяги, которые можно реализовать по сцепным свойствам дороги, называют силой тяги по сцеплению P_φ . Основными факторами, влияющими на силу тяги по сцеплению, являются:

• нагрузка на ведущие колеса (сцепная нагрузка) и ее распределение по колесам;
• качество и состояние дорожного покрытия (грунта);
• удельное давление шин на дорогу;
• тип силовой передачи;
• состояние протектора шин.

Рассмотрим влияние каждого из этих факторов на силу тяги по сцеплению.

Сцепная нагрузка

При увеличении нагрузки на колесо увеличивается сила трения и сила зацепления. Сила тяги по сцеплению прямо пропорциональна сцепной нагрузке G_φ или нормальным реакциям на ведущих колесах:

где φ_x – коэффициент продольного сцепления колеса с опорной поверхностью.

А поскольку сила тяги определяется максимальным значением касательной реакции дороги, которая пропорциональна R_z , то можно записать:

где R_{x max} – максимально возможная продольная реакция по сцеплению.

Коэффициент φ_x определяется экспериментальным путем чаще всего при скольжении колеса в тормозном режиме, т. е. при протаскивании полностью заторможенного колеса:

Дорожное покрытие

Качество и состояние дорожного покрытия являются решающими факторами, влияющими на коэффициент сцепления φ_x . При движении автомобиля по дороге с твердым покрытием коэффициент продольного сцепления колеса с опорной поверхностью зависит от шероховатости и влажности дороги, наличия пыли и грязи. При этом даже тонкий слой воды на дорожном покрытии может не только существенно снизить φ_x , но и создавать подъемную силу, еще больше снижая сцепление шины с дорогой. Такой же и даже более выраженный эффект может создавать жидкая грязь на дороге.
Следует учитывать, что подъемная сила, возникающая при движении по мокрым и грязным дорогам, пропорциональная квадрату скорости движения автомобиля, и при большой скорости может вызвать аквапланирование, когда полностью прерывается контакт между шинами и дорогой.

Удельное давление на дорогу

Удельное давление шины на дорогу определяется площадью опорной поверхности шины и весом автомобиля, приходящимся на данное колесо. Регулировать удельное давление шины на дорогу можно изменением давления в шине – при снижении давления увеличивается площадь опорной поверхности и удельное давление снижается, и наоборот – при увеличении давления воздуха в шине уменьшается площадь опорной поверхности, что приводит к увеличению удельного давления колеса на дорогу.

Очевидно, что увеличение опорной поверхности шины с дорогой приводит к увеличению силы сцепления, особенно, на грунтовых дорогах, поскольку в зацеплении участвует большее количество грунтозацепов протектора покрышки.

При движении по влажным дорожным покрытиям повышенное удельное давление (давление в шинах) может благотворно сказаться на сцеплении шин с дорогой из-за выдавливания влаги из-под колес.

Удельное давление, оказываемое колесом на опорную поверхность, в некоторой степени зависит и от размеров шины – от ее диаметра и ширины. При увеличении диаметра колеса сегмент дуги, по которой осуществляется контакт шины с дорогой, имеет бȯльшую длину, чем опорный сегмент маленького колеса. Широкая шина создает колесу опору большей площади, чем узкая.

Влияние на сцепные свойства типа трансмиссии

Многочисленные опыты показали, что применение бесступенчатых трансмиссий обеспечивает повышение силы тяги по сцеплению. Главную роль здесь играет возможность плавного изменения величины тяговых моментов на ведущих колесах, без рывков и резких толчков.
В трансмиссиях, оснащенных ступенчатыми коробками передач, потеря сцепления колес с опорной поверхностью чаще всего имеет место во время переключения передач, сопровождающихся резким изменением величины крутящего момента на колесах.

Влияние конструкции шин

Важную роль в повышении сцепления колеса с дорогой играют рисунок протектора, а для шин повышенной проходимости размеры (особенно, высота) грунтозацепов протектора. Протектор шин легковых автомобилей обычной проходимости, как правило, имеет мелкий рисунок, обеспечивающий хорошее сцепление с твердым покрытием.
Наименьший коэффициент сцепления при прочих равных условиях у шин с изношенным рисунком протектора. Поэтому использование автомобилей с такими шинами запрещено.

Недостаточная величина коэффициента сцепления является причиной многих дорожно-транспортных происшествий. Для обеспечения безопасности дорожного движения его величина не должна быть меньше 0,4.

На дорогах с низкими сцепными свойствами коэффициент сцепления φx снижается до 0,2 и становится соизмеримым с коэффициентом сопротивления качению f . Это означает,что движение может оказаться невозможным из-за отсутствия запаса силы тяги по сцеплению. Следовательно, условие качения колес без скольжения можно представить в виде

Если сила тяги Р_т меньше силы сцепления Р_φ , ведущие колеса катятся без буксования. Если сила тяги превысит силу сцепления колес с дорогой, ведущие колеса будут пробуксовывать, а для движения использоваться лишь часть силы тяги, равная φR_z . Остальная часть силы тяги вызывает ускоренное вращение буксующих колес. Буксование колес связано со значительными потерями энергии на трение шин о дорогу и разрушение опорной поверхности.

Не менее вредное влияние на сцепную тягу автомобиля и его устойчивость на дороге оказывает скольжение заторможенных колес по твердому дорожному покрытию (блокировка колес). В этом случае изношенные частицы шины, попадая на опорную поверхность колеса и дороги, вызывают эффект «смазки», существенно снижая сцепные свойства шины. Это явление явилось причиной появления тормозных систем с антиблокировочными устройствами (АБС).

Условия возможности движения автомобиля

Согласно уравнению силового баланса (1) равномерное безостановочное движение автомобиля возможно лишь при условии

Выполнение этого условия для безостановочного движения автомобиля необходимо, но недостаточно, поскольку оно возможно лишь при отсутствии буксования ведущих колес.

Учитывая формулу (2) условие безостановочного движения можно выразить так:

Если суммарная сила сопротивления движению больше силы тяги, то двигатель автомобиля заглохнет. Если сила тяги превысит силу сцепления, ведущие колеса начнут пробуксовывать.

Формула (4) справедлива для полноприводных автомобилей, где вертикальная реакция R_z на ведущих колесах равна весу автомобиля. Для переднеприводных автомобилей вместо R_z следует подставить R_z1 , для заднеприводных – R_z2 .

Мощностной баланс автомобиля

Иногда вместо силового баланса, характеризуя возможность движения автомобиля, пользуются мощностным балансом. Мощность силы определяется ее модульной величиной и скоростью v движения тела под действием этой силы. Если умножить все члены уравнения силового баланса (1) на v /1000, получим уравнение мощностного баланса:

где N_т – тяговая мощность:

N_т = Р_тv/ 1000 = М_кi_трη_трv/ 1000 r = N_еη_тр
(здесь N_е – эффективная мощность двигателя, η_тр – КПД трансмиссии, i_тр – передаточное число трансмиссии);

N_α – мощность, затрачиваемая на преодоление подъема:

N_f – мощность, затрачиваемая на преодоление сопротивления качению:

N_ω — мощность, затрачиваемая на преодоление сопротивления воздуха:

N_j – мощность, затрачиваемая на преодоление сопротивления разгону:

N_ψ – мощность, затрачиваемая на преодоление сопротивления дороги:

Уравнение мощностного баланса устанавливает соотношения между мощностью, подводимой к ведущим колесам автомобиля и мощностью, необходимой для преодоления сопротивления движению автомобиля.

Используя уравнение мощностного баланса строят графики мощностного баланса для движения автомобиля на каждой из передач. Такие графики удобно использовать при сравнительной оценке тяговых свойств автомобиля графическими методами.

Видео:Урок 12. Равномерное прямолинейное движениеСкачать

8 Уравнение движения автомобиля

7.1 Силы сопротивления движению и мощности, затрачиваемые на их преодоление

7. 2. Уравнение движения автомобиля

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

7. 1 Силы сопротивления движению и мощности, затрачиваемые на их преодоление

Силами сопротивления называются силы, препятствующие Движению автомобиля. Эти силы направлены против его движе­ния.

При движении на подъеме, характеризуемом высотой Н_п, длиной проекции В_п на гори­зонтальную плоскость и углом подъема дороги а, на автомобиль действуют следующие силы со­противления (рис. 7.1): сила со­противления качению Р_к, равная сумме сил сопротивления каче­нию передних (Р_К1) и задних (Р_К2) колес, сила сопротивления подъе­му Р_п, сила сопротивления воз­духа Р_в и сила сопротивления раз­гону Р_и. Силы сопротивления ка­чению и подъему связаны с особенностями дороги. Сумма этих сил называется силой сопротивления дороги Р_д.

Рис. 7.1. Силы сопротивления движению автомобиля

Сила сопротивления качению

Возникновение силы сопротивления качению при движении обусловлено потерями энергии на внутреннее трение в шинах, поверхностное трение шин о дорогу и образование колеи (на де­формируемых дорогах).

Видео:Решение графических задач на равномерное движениеСкачать

Рекомендуемые файлы

О потерях энергии на внутреннее трение в шине можно судить по рис. 7.2, на котором приведена зависимость между вертикаль­ной нагрузкой на колесо и деформацией шины — ее прогибом f_ш.

При движении колеса по неровной поверхности шина, испы­тывая действие переменной нагрузки, деформируется. Линия Оа, которая соответствует возрастанию нагрузки, деформирующей шину, не совпадает с линией аО, отвечающей снятию нагрузки. Площадь области, заключенной между указанными кривыми, ха­рактеризует потери энергии на внутреннее трение между отдель­ными частями шины (протектор, каркас, слои корда и др.).

Потери энергии на трение в шине называются гистерезисом, а линия ОаО — петлей гистерезиса.

Потери на трение в шине необратимы, так как при деформа­ции она нагревается и из нее выделяется теплота, которая рассе­ивается в окружающую среду. Энергия, затрачиваемая на дефор­мацию шины, не возвращается полностью при последующем вос­становлении ее формы.

Сила сопротивления качению Р_к достигает наибольшего зна­чения при движении по горизонтальной дороге. В этом случае

Рк =fG, где G — вес автомобиля, Н; f — коэффициент сопротивления качению.

Рис. 7.2. Потери энергии на внутреннее трение в шине:

а — точка, соответствующая мак­симальным значениям нагрузки и прогиба шины

Рис. 7.3. Зависимости силы сопротив­ления качению Р_к и мощности N_K, не­обходимой для преодоления этого со­противления, от скорости автомобиля

При движении на подъеме и спуске сила сопротивления каче­нию уменьшается по сравнению с Р_к на горизонтальной дороге, и тем значительнее, чем они круче. Для этого случая движения сила сопротивления качению

где а — угол подъема, °.

Зная силу сопротивления качению, можно определить мощ­ность, кВт, затрачиваемую на преодоление этого сопротивления:

где v — скорость автомобиля, м/с. Для горизонтальной дороги cos 0° = 1 и

Зависимости силы сопротивления качению Р_к и мощности N_K от скорости автомобиля v показаны на рис. 7.3.

Коэффициент сопротивления качению

Коэффициент сопротивления качению существенно влияет на потери энергии при движении автомобиля. Он зависит от многих конструктивных и эксплуатационных факторов и определяется экспериментально. Его средние значения для различных дорог при Нормальном давлении воздуха в шине составляют 0,01 . 0,1.

Рис 7.4. Зависимости коэффициента сопротивления качению от

скорости движения (а), давления воздуха в шине (б) и момента,

передаваемого через колесо (в)

Рассмотрим влияние различных факторов на коэффициент со­противления качению.

Скорость движения. При изменении скорости движения в ин­тервале 0. 50 км/ч коэффициент сопротивления качению изме­няется незначительно и его можно считать постоянным в указан­ном диапазоне скоростей.

При повышении скорости движения за пределами указанного интервала коэффициент сопротивления качению существенно уве­личивается (рис. 7.4, а) вследствие возрастания потерь энергии в шине на трение.

Коэффициент сопротивления качению в зависимости от ско­рости движения можно приближенно рассчитать по формуле

где v — скорость автомобиля, км/ч.

Тип и состояние покрытия дороги. На дорогах с твердым по­крытием сопротивление качению обусловлено главным образом деформациями шины.

При увеличении числа дорожных неровностей коэффициент сопротивления качению возрастает.

На деформируемых дорогах коэффициент сопротивления ка­чению определяется деформациями шины и дороги. В этом случае он зависит не только от типа шины, но и от глубины образую­щейся колеи и состояния грунта.

Значения коэффициента сопротивления качению при рекомен­дуемых уровнях давления воздуха и нагрузки на шину и средней скорости движения на различных дорогах приведены ниже:

Асфальто- и цементобетонное шоссе:

в хорошем состоянии. 0,007. 0,015

в удовлетворительном состоянии. 0,015. 0,02

Гравийная дорога в хорошем состоянии. 0,02. 0,025

Булыжная дорога в хорошем состоянии. 0,025. 0,03

Грунтовая дорога сухая, укатанная. 0,025. 0,03

Обледенелая дорога, лед. 0,015. 0,03

Укатанная снежная дорога. 0,03. 0,05

Тип шины. Коэффициент сопротивления качению во многом зависит от рисунка протектора, его износа, конструкции каркаса и качества материала шины. Изношенность протектора, уменьше­ние числа слоев корда и улучшение качества материала приводят к падению коэффициента сопротивления качению вследствие снижения потерь энергии в шине.

Давление воздуха в шине. На дорогах с твердым покрытием при уменьшении давления воздуха в шине коэффициент сопро­тивления качению повышается (рис. 7.4, б). На деформируемых дорогах при снижении давления воздуха в шине уменьшается глу­бина колеи, но возрастают потери на внутреннее трение в шине. Поэтому для каждого типа дороги рекомендуется определенное давление воздуха в шине, при котором коэффициент сопротивле­ния качению имеет минимальное значение.

Нагрузка на колесо. При увеличении вертикальной нагрузки на колесо коэффициент сопротивления качению существенно возрастает на деформируемых дорогах и незначительно — на до­рогах с твердым покрытием.

Момент, передаваемый через колесо. При передаче момента через колесо коэффициент сопротивления качению возрастает (рис. 7.4, в) вследствие потерь на проскальзывание шины в месте ее контакта с дорогой. Для ведущих колес значение коэффициента сопротивления качению на 10. 15 % больше, чем для ведомых.

Коэффициент сопротивления качению оказывает существен­ное влияние на расход топлива и, следовательно, на топливную экономичность автомобиля. Исследования показали, что даже не­большое уменьшение этого коэффициента обеспечивает ощути­мую экономию топлива. Поэтому неслучайно стремление конст­рукторов и исследователей создать такие шины, при использова­нии которых коэффициент сопротивления качению будет незна­чительным, но это весьма сложная проблема.

Сила сопротивления подъему

Вес автомобиля, который движется на подъеме, можно разло­жить на две составляющие (см. рис. 7.1): параллельную и перпен­дикулярную поверхности дороги. Составляющая силы тяжести, параллельная поверхности дороги, представляет собой силу со­противления подъему, Н:

где G — вес автомобиля, Н; a — угол подъема, °.

Рис. 7.5. Зависимости силы сопро­тивления подъему Р_п и мощности N_п, необходимой для его преодоле­ния, от скорости автомобиля

В качестве характеристики кру­тизны подъема наряду с углом α используют величину i, называе­мую уклоном и равную i = H/B_n, где Н_п — высота подъема; B_n — длина его проекции на горизон­тальную плоскость. Сила сопротивления подъему может быть направлена как в сто­рону движения, так и против него. В процессе подъема она дей­ствует в направлении, противоположном движению, и является силой сопротивления движению. При спуске эта сила, направлен­ная в сторону движения, становится движущей.

Зная силу сопротивления подъему, можно определить мощ­ность, кВт, необходимую для преодоления этого сопротивления:

где v — скорость автомобиля, м/с.

Зависимости силы сопротивления подъему Р_п „ и мощности N_n, необходимой для преодоления этого сопротивления, от скорости автомобиля v приведены на рис. 7.5.

Сила сопротивления дороги

Сила сопротивления дороги представляет собой сумму сил со­противления качению и сопротивления подъему:

Выражение в скобках, характеризующее дорогу в общем слу­чае, называется коэффициентом сопротивления дороги:

При малых углах подъема (не превышающих 5°), характерных для большинства автомобильных дорог с твердым покрытием, ко­эффициент сопротивления дороги

Сила сопротивления дороги в этом случае

Зная силу сопротивления доро­ги, можно определить мощность, кВт, необходимую для его преодо­ления:

где скорость автомобиля v выражена в м/с, вес G — в Н, мощ­ность N_Д — в кВт.

Зависимости силы сопротивления дороги Р_в и мощности N_Д, затрачиваемой на его преодоление, от скорости автомобиля v представлены на рис. 7.6.

Сила сопротивления воздуха

При движении действие силы сопротивления воздуха обуслов­лено перемещением частиц воздуха и их трением о поверхность автомобиля. Если он движется при отсутствии ветра, то сила со­противления воздуха, Н:

тогда как при наличии ветра

где k_в — коэффициент сопротивления воздуха (коэффициент об­текаемости), Н-с 2 /м 4 ; F_a — лобовая площадь автомобиля, м 2 ; v — скорость автомобиля, м/с; v_B — скорость ветра, м/с (знак «+» со­ответствует встречному ветру, знак «-» — попутному).

Коэффициент сопротивления воздуха, зависящий от формы и качества поверхности автомобиля, определяется эксперимен­тально при продувке в аэродинамической трубе.

Рис. 7.7. Площади лобового сопротивления легкового (а) и грузового

Коэффициент сопротивления воздуха, Н-с 2 /м 4 , составляет 0,2. 0,35 для легковых автомобилей, 0,35. 0,4 — для автобусов и 0,6. 0,7 — для грузовых автомобилей. При наличии прицепов со­противление воздуха увеличивается, так как возрастает наружная поверхность трения и возникают завихрения воздуха между тягачом и прицепами. При этом каждый прицеп вызывает увеличение коэффициента k_в в среднем на 15. 25 %.

Лобовая площадь автомобиля зависит от его типа (рис. 7.7). Ее приближенное значение, м 2 , можно вычислить по следующим фор­мулам:

F_A = ВН_а — для грузовых автомобилей и автобусов;

где В — колея колес автомобиля, м; Н_а — наибольшая высота автомобиля, м; B_а — наибольшая ширина автомобиля, м.

Мощность, кВт, затрачиваемая на преодоление сопротивле­ния воздуха:

— при отсутствии ветра;

— при наличии ветра.

Зависимости силы сопротивления воздуха Р_в и мощности N_B, необхо­димой для преодоления этого сопро­тивления, от скорости автомобиля v приведены на рис. 7.8.

Рис. 7.8. Зависимости силы сопротивле­ния воздуха Р_в и мощности N_b, необхо­димой для преодоления этого сопротив­ления, от скорости автомобиля

Сила сопротивления разгону

Сила сопротивления разгону воз­никает вследствие затрат энергии на раскручивание вращающихся частей двигателя и трансмиссии, а также колес при движении автомобиля с ускорением.

Сила сопротивления разгону, Н:

=

где G — вес автомобиля, Н; g — ус­корение силы тяжести, м/с 2 ; _вр — коэффициент учета вращающихся масс автомобиля; j — ускорение ав­томобиля, м/с 2 .

Мощность, кВт, затрачиваемая на разгон:

Зависимости силы сопротивления разгону Р_и и мощности N_K, необходимой для преодоления этого сопротивления, от скорости автомобиля v представлены на рис. 7.9.

Рис. 7.9. Зависимости силы сопротивления разгону Р_я и мощности /У_и, необходимой для преодоления этого сопро­тивления, от скорости авто­мобиля

Коэффициент учета вращающихся масс

Этот коэффициент учитывает дополнительное сопротивление разгону автомобиля, вызванное раскручиванием вращающихся ча­стей двигателя, трансмиссии и колес.

Коэффициент учета вращающихся масс показывает, во сколь­ко раз мощность, затрачиваемая на разгон автомобиля, больше мощности, необходимой для установившегося движения:

где J_M — момент инерции маховика; u_Т, _Чтр — передаточное число и КПД трансмиссии; J_сум — суммарный момент инерции всех ко­лес автомобиля.

Коэффициент учета вращающихся масс для автомобиля с пол­ной нагрузкой можно приближенно рассчитать по формуле

где и_к, и_д — передаточные числа основной и дополнительной ко­робок передач.

Видео:Силы действующие на автомобиль при движении Подробный видеоурокСкачать

7.2. Уравнение движения автомобиля

Для вывода уравнения движения рассмотрим разгон автомоби­ля на подъеме (рис. 7.10).

Спроецируем все силы, действующие на автомобиль, на по­верхность дороги:

(7.1)

Подставим в формулу (7.1) касательные реакции дороги R_X1 и R_X2, объединим члены с коэффициентом сопротивления каче­нию f и члены с ускорением j и, принимая во внимание соотно­шения f(R_Zl + R_Z2)- P_k и /*, + Л₂ = Jк , а также коэффициент уче­та вращающихся масс, получим уравнение движения автомобиля в общем виде:

или

(7.2)

Уравнение движения автомобиля выражает связь между дви­жущими силами и силами сопротивления движению. Оно позво­ляет определить режим движения автомобиля в любой момент.

Так, например, при установившемся (равномерном) движе­нии

Из уравнения (7.2) следует, что безостановочное движение автомобиля возможно только при условии

Ещё посмотрите лекцию «18 Дизайн молекул лекарств» по этой теме.

Рис. 7.10. Схема сил, действую­щих на автомобиль на подъеме

данное неравенство связыва­ет конструктивные параметры ав­томобиля с эксплуатационными факторами, обусловливающими сопротивление движению. Одна­ко оно не гарантирует отсутствия буксования ведущих колес. Безо­становочное движение автомоби­ля без буксования ведущих колес возможно лишь при соблюдении условия

Р_сц Р_Т Р_Д + Р_В.

Условие равномерного движения при отсутствии буксования ведущих колес записывается в виде

Р_сц Р_Т = Р_Д + Р_В

🌟 Видео

Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Задача на движение (автомобиль и мотоциклист)Скачать

Равномерное прямолинейное движение - физика 9Скачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Прямолинейное движение. 10 класс.Скачать

Физика. Решение задач. Уравнение движения тела,движущегося равномерно. Выполнялка 26Скачать

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать

№ 1-100 - Физика 10-11 класс РымкевичСкачать

Физика 10 класс. Скорость. Равномерное прямолинейное движениеСкачать