Силы, действующие на агрегат.В динамическом отношении машинно-тракторный агрегат представляет собой систему твердых тел, связанных между собой жесткими и упругими связями. Агрегат движется и работает в результате взаимодействия сил, действующих на него.
Источником энергии для агрегата с трактором, оборудованным тепловым двигателем, является топливо. Тракторный двигатель, преобразуя энергию топлива в механическую, реализует
ее в виде крутящего момента Ме. Весь момент (для прицепного агрегата) или часть его (для приводного) через трансмиссию передается движителю, в результате чего при достаточном сцеплении трактора с почвой создается движущая сила F. Она сообщает трактору и машинам ускорение при трогании с места и при изменении скорости движения, а также преодолевает их сопротивление при установившемся движении (постоянной скорости).
На рисунке представлена общая схема внешних сил, действующих на трактор, при его движении на подъем с углом а.
В направлении движения можно выделить следующие силы: 1) силу F, движущую агрегат; 2) силы сопротивления — тяговое сопротивление рабочей части агрегата Rа, возникающее в связи с перемещением и выполнением рабочей машиной технологического процесса; сопротивление движению трактора Pf, возникающее в связи с деформацией почвы ходовой частью, механическими потерями и т. п.; сопротивление воздушной среды Рвозд и сопротивление подъему (спуску) трактора Pα= ±Gsinα (G —вес трактора*). Общее сопротивление Pc=Rа + Pf + PB03Д.± Pα
Среди внешних сил сопротивления, действующих на агрегат решающее значение имеет сопротивление рабочей части агрегата (рабочей машины) Rа.
В направлении, перпендикулярном к плоскости движения действуют следующие внешние силы: 1) составляющая веса трактора G cosα; 2) составляющие реакции почвы, действующие на ведущие и направляющие колеса RB и RH (для колесного трактора) или Rосн (для гусеничного); 3) составляющая от воздействия рабочей машины Rв.м.
Работа и движение агрегата возможны только при определенном соотношении скорости движения v, приведенной массы агрегата т и сил, действующих на агрегат (трактор) в направлении движения. Это соотношение определяется уравнением движения
В ряде случаев сельскохозяйственные агрегаты характеризуются переменной массой машин (главным
образом из-за поступления или разгрузки материалов). В этом случае уравнение движения агрегата имеетболее сложный вид. В эксплуатационных расчетах приведенную массу машин принимают постоянкой.
Вследствие непрерывного изменения условий: свойств почвы глубины обработки, микрорельефа и других, которые имеют случайный (в вероятностно-статистическом смысле) характер, все величины, входящие в уравнение движения, в процессе работы агрегата также имеют случайный характер и непрерывно изменяются. В связи с этим изменяется (как правило, по закону нормального распределения) и ускорение dυ/dt. Это сказывается на качестве технологического процесса и ухудшает работу агрегата. Для каждого технологического процесса существуют допустимые пределы вариации ускорения.
Если движущая сила F и силы сопротивления Рс изменяются сравнительно мало, то ускорение dυ/dt зависит только от приведенной массы агрегата: чем она больше, тем меньше ускорение. Поэтому при прочих равных условиях агрегаты, имеющие большую массу, устойчивее в своем движении.
Поскольку m dυ/dt представляет собой приведенную силу инерции pj, направленную в сторону, противоположную направлению ускорения, то силы, действующие в направлении движения агрегата, можно представить уравнением, которое называется тяговым балансом агрегата:
Так как скорости движения машинно-тракторных агрегатов сравнительно небольшие, сопротивление воздушной среды невелико и им обычно пренебрегают, принимая Рвозд = 0.
В большинстве практических расчетов по ЭМТП (кроме процесса разгона и торможения агрегата), имея в виду закон нормального распределения ускорения, его считают по среднему значению, (dv/dt = 0), т. е. принимают, что движение установившееся.
В этом случае тяговый баланс определяется тем, что движущая сила равна сумме сил сопротивления, которые она преодолевает:
В случае когда требуется учитывать мгновенные значения действующих сил (при рассмотрении качества технологического процесса, прочности и вибрации частей трактора, действия автоматических устройств, при расчете ряда экономических показателей и т. д.), следует исходить из неустановившегося характера движения и принимать в расчет ±Рj.
Как видно из уравнений и из рисунка тяговый баланс определяет соотношение фактических усилий, причем в случае установившегося движения тяговое усилие Рт = Rа, а движущая сила F = PC. Предельные же (или оптимальные) значения этих величин характеризуют эксплуатационные свойства трактора и зависят вовсе не от значения преодолеваемых сопротивлений, а от возможностей (свойств) самого трактора и его двигателя.
Видео:13-2 Работа генераторного агрегата на нагрузку. Уравнение движения ротора генератораСкачать

Сельскохозяйственные и мелиоративные машины
Видео:Физика - уравнения равноускоренного движенияСкачать

Тяговый и мощностной баланс трактора
Тяговый баланс трактора
На рисунке 1 представлена схема внешних сил, действующих на гусеничный трактор, движущийся ускоренно и на подъеме с углом α .
Рисунок 1. Схема внешних сил, действующих на трактор
В направлении движения действует только одна активная сила, это сила движущая агрегат F .
Все другие силы, направленные в противоположную сторону движения трактора — это силы сопротивления:
— составляющая тягового сопротивления рабочей части агрегата Rа , возникающая в связи перемещением и выполнением рабочими машинами технологического процесса (приложенная к трактору она называется тяговым усилием Pкр ),
— сопротивление движению самого трактора со стороны опорной поверхности Pf ,
— сопротивление воздушной среды Pв ,
— силы инерции Pj ,
— дополнительное сопротивление на преодоление подъема (спуска) Pα .
Сумма сил сопротивления движения трактора может быть выражена формулой:
Так как mпр•dv/dt представляет собой приведенную силу инерции Pj , то уравнение движения агрегата с учетом формулы (1) может быть представлена уравнением, в котором сила, движущая агрегат, равна алгебраической сумме внешних сил, действующих на движущийся трактор:
Формула (2) называется уравнением тягового баланса трактора .
В направлении, перпендикулярном движению агрегата, действуют следующие внешние силы: составляющая веса трактора m∙g∙cosα , составляющая от воздействия рабочих машин на трактор Rвм = Pкр∙tgβ и соответствующие реакции почвы Rосн (для гусеничного трактора) или действующие на ведущие Rв и направляющие колеса Rн (колесных тракторов).
Сопротивление движению трактора со стороны почвы зависит от конструкции ходового аппарата и веса трактора, свойств и неровностей почвы, величины тягового усилия, скорости движения. Все эти факторы находятся в сложной взаимосвязи и определение сопротивления движению от каждого фактора в отдельности весьма затруднительно.
Поэтому для практических расчетов сопротивления передвижению используют упрощенную зависимость:
где m – эксплуатационная масса трактора, кг;
mм – масса рабочей машины, кг;
р – коэффициент, показывающий, какая часть массы рабочей машины нагружает трактор;
f – коэффициент пропорциональности, обычно называемый коэффициентом сопротивления передвижения;
g – ускорение свободного падения, м/с 2 .
Понятие эксплуатационной массы включает конструктивную массу трактора, массу тракториста (по стандарту 75 кг), массу балластных грузов и возимого инструмента, массу полной заправки всех емкостей горюче-смазочными материалами и охлаждающей жидкостью и массу устанавливаемого на тракторе дополнительного оборудования, указанного в технической документации.
Из рисунка 1 видно, что сопротивление подъему (спуску) выражается зависимостью:
Поскольку углы подъемов (спусков) небольшие, то без большой ошибки можно принять sinα ≈ tgα , а tgα = h/l = i (то есть отношение величины подъема h к величине ее заложения l ). Тогда сопротивление подъему можно представить более удобной для расчета формулой:
Из формулы (5) видно, что при подъеме (спуске) на один процент (градус) сопротивление машины изменяется (увеличивается или уменьшается в зависимости от знака) на один процент ее веса.
Сопротивление воздушной среды Pв обычно учитывается при относительной скорости воздушного потока более 18 км/ч.
Так как скорости движения машинно-тракторных агрегатов сравнительно небольшие то, сопротивление воздушной среды невелико и им обычно при расчетах пренебрегают, принимая Рв = 0 .
Величина dv/dt зависит от большого числа случайных факторов и, как показывают многочисленные опытные данные, распределена по нормальному закону. Поэтому наиболее вероятной средней величиной ускорения прямолинейно-поступательного движения является нуль. Это служит основанием для упрощения расчетов по составлению агрегатов, принимая движение установившимся и Pj = 0 .
Силы инерции Pj обычно учитывают при расчете разгона или торможения МТА, когда ускорение может достигать 10 м/с 2 .
В большинстве практических расчетов по составлению МТА принимают, что движение установившееся ( dv/dt = 0 ) и сопротивление воздушного потока невелико.
В этом случае уравнение тягового баланса трактора имеет вид:
Как видно из уравнения (6) и рисунка 1 в случае установившегося движения тяговое усилие трактора Ркр = Rа , движущая агрегат сила F = Pс .
Мощностной баланс трактора
Как известно, мощность — это произведение силы на скорость движения тела под действием этой силы. Поэтому, аналогично тому, как составляется баланс сил, описывается и баланс мощностей, называемый уравнением мощностного баланса.
Уравнение мощностного баланса показывает, на какие составляющие расходуется эффективная мощность двигателя Nе , и в общем виде записывается:
где Nтр — потери мощности в трансмиссии, кВт;
Nf — потери мощности на качение (самопередвижение) трактора;
Nб — потери мощности на буксование;
Nа — потери мощности на преодоление подъема;
Nj — потери мощности на преодоление сил инерции;
NВОМ — мощность, отводимая через вал отбора мощности трактора (ВОМ);
Nв — потери мощности на преодоление сопротивления воздуха;
Nкр — полезная мощность на крюке.
Обычно для оценки тяговых и мощностных качеств трактора мощностной баланс рассматривают для случая движения по горизонтальной дороге в установившемся режиме без отбора мощности через ВОМ. При этом потерей мощности на преодоление сопротивления воздуха пренебрегают. При постоянной скорости движения машины не учитывают и потери на преодоление сил инерции.
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Уравнение движения машинного агрегата и его решение
Составляем уравнение движения машинного агрегата, которое может быть записано (на основании уравнения Лагранжа 2-го рода) в форме:
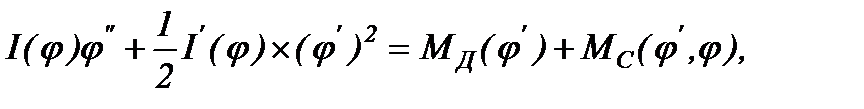
где: 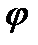

Интегрирование уравнения ведется в предположении, что закон движения может быть представлен в виде суммы равномерного вращения и малых периодических колебании


ψ(t) – динамическое отклонение угла поворота от среднего значения 
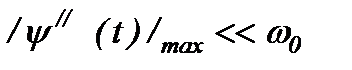
Преобразуем дифференциальное уравнение:
-в левую часть перенесем слагаемые, не зависящие от угла поворота кривошипного вала;
-в правую часть перенесем слагаемые, зависящие от угла поворота кривошипного вала.
Тогда уравнение движения машинного агрегата, может быть записано в виде:
Уравнение решается методом последовательных приближений.
Исходное приближение определяется как решение уравнения:

Эксплуатационный момент двигателя приведенный к кривошипному валу рабочей машины равен: 
Определяем среднее значение угловой скорости кривошипного вала рабочей машины:

В дальнейшем дифференциальное уравнение решаем в такой последовательности:
Определим амплитудные значения возмущающего момента для трех гармоник по зависимости:

аналогично для n=2,3 значения амплитудного значения возмущающего момента представлены в виде таблицы 2.10.
Таблица 2.10 Значения амплитудного значения возмущающего
| L1 | L2 | L3 |
| 183,719254 | 9,40606594 | 29,5476978 |
Определим изменения возмущающих моментов


Для n=1 , 


Аналогично определяем для 
Таблица 2.11 Значения возмущающего момента
Угол поворота кривошипа  ° ° | L1(f) | L2(f) | L3(f) | L(f)=L1(F)+L2(F)+L3(F) |
| -168,897 | 9,067161 | 25,2132287 | -134,61695 | |
| -110,122 | 2,366671 | -15,406477 | -123,16208 | |
| -21,84 | -6,70049 | -25,213229 | -53,753759 | |
| 72,29422 | -9,06716 | 15,4064775 | 78,6335337 | |
| 147,0573 | -2,36667 | 25,2132287 | 169,903855 | |
| 182,4165 | 6,70049 | -15,406477 | 173,710506 | |
| 168,8973 | 9,067161 | -25,213229 | 152,751269 | |
| 110,1223 | 2,366671 | 15,4064775 | 127,895424 | |
| 21,84004 | -6,70049 | 25,2132287 | 40,3527777 | |
| -72,2942 | -9,06716 | -15,406477 | -96,767856 | |
| -147,057 | -2,36667 | -25,213229 | -174,6372 | |
| -182,416 | 6,70049 | 15,4064775 | -160,30952 | |
| -168,897 | 9,067161 | 25,2132287 | -134,61695 |
По данным таблицы 2.11 строим графики изменения возмущающего момента



где:YL – отрезок изображающий L, мм.
Определим углы сдвига вектора возмущающего момента n-й гармоники по отношению к вектору постоянного момента L0



Аналогично определяем 
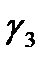
Таблица 2.12 Численные значения углов сдвига возмущающего момента
cos  |  | 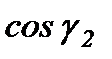 |  |  |  |
| -0,91861 | -0,39516 | 0,963933 | 0,266144 | 0,853161 | 0,521648 |
 =203,2757 0 =203,2757 0 |  =15,43496 0 =15,43496 0 |  =31,44285 0 =31,44285 0 |
По данным таблицы 2.12 строим диаграмму углов сдвига вектора возмущающего момента.
Определим амплитудные значения динамического отклонения угловой координаты:

Таблица 2.13 Численные значения амплитуды
| А1.м | А2.м | А3.м |
| 0,06412774 | 0,00164142 | 0,00343683 |
Определим величину угла сдвига амплитуды угловой координаты n-й гармоники

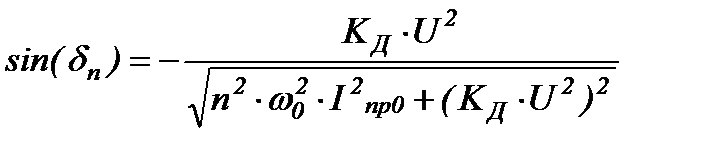
Аналогично определяем 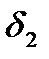
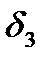
Таблица 2.14 Численные значения угла сдвига амплитуды угловой координаты
cos  |  |  |  |  |  |
| -0,00884 | -0,99996 | -0,01767 | -0,99984 | -0,0265 | -0,99965 |
 =269,4937 0 =269,4937 0 |  =268,9874 0 =268,9874 0 |  =268,4813 0 =268,4813 0 |
По данным таблицы 2.14 строим диаграмму углов сдвига вектора угловой скорости
Определим динамическое отклонение по углу поворота кривошипного вала

Для 

Определим динамическое отклонение по угловой скорости кривошипного вала

Для 

Определим угловое ускорение кривошипного вала

Для 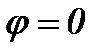
Аналогично определяем 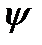



Таблица 2.15 Значения динамических отклонений
Угол поворота кривошипного вала  | Динамическое отклонение  ,м ,м | Динамическое отклонение 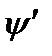 ,с -1 ,с -1 | Угловое ускорение  ,с -2 ,с -2 |
| -0,02246 | -0,4893944 | 0,81967661 | |
| -0,04633 | -0,4492857 | 1,91370668 | |
| -0,06411 | -0,2034233 | 8,01451866 | |
| -0,06262 | 0,34010907 | 9,4675229 | |
| -0,03889 | 0,612554 | 3,23563477 | |
| -0,00653 | 0,63124961 | -1,4908813 | |
| 0,02327 | 0,55550419 | -1,1692865 | |
| 0,049493 | 0,46777026 | -3,2782211 | |
| 0,066465 | 0,15579801 | -9,0294231 | |
| 0,061812 | -0,3415444 | -9,117913 | |
| 0,035726 | -0,6310386 | -1,8711204 | |
| 0,004179 | -0,5836244 | 2,50578573 |
Поданным таблицы 2.15 строим графики:
график изменения динамического отклонения по углу поворота кривошипного вала 



где:Y 

график изменения динамического отклонения угловой скорости кривошипного вала

   | (248) |
где:Y 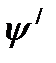

график изменения углового ускорения кривошипного вала 



Определим коэффициент неравномерности хода машинного агрегата
Определенный коэффициент выше заданного: δ =0,163>[δ]=0,13, необходимо определить дополнительную массу для чего производим расчет маховика.
🔥 Видео
Урок 7. Механическое движение. Основные определения кинематики.Скачать

Поступательное и вращательное движения.Скачать

Закон рычагаСкачать

Уравнение равномерного движения. Решение задач по теме.Скачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Равноускоренное движение. Вывод формулСкачать

Урок 89 (осн). Задачи на вращательное движение - 1Скачать

Урок 15. Решение задач на графики движенияСкачать

Поступательное и вращательное движенияСкачать

Вращательное движение. 10 класс.Скачать

Функция Лагранжа. Уравнения Лагранжа. Интегралы движения.Скачать

Физика 10 класс (Урок№6 - Инерциальные системы отсчета и принцип относительности в механике.)Скачать

1 3 Кинематика вращательного движенияСкачать

Урок 246 Условия существования постоянного тока. Электродвижущая силаСкачать

10 класс - Физика - Кинематические и динамические характеристики движенияСкачать

Механизм преобразования вращательного движения в поступательноеСкачать

Пример 1. Задача "Машина Атвуда"Скачать




















