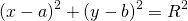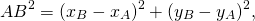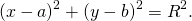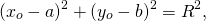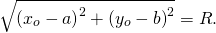Уравнение дуги окружности в декартовой системе координат

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Видео:Длина дуги окружности. 9 класс.Скачать

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Видео:Уравнение окружности (1)Скачать

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Окружность

Определение: замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра О), лежащей в той же плоскости, что и кривая.

Определения связанные с окружностью

Хорда: отрезок, соединяющий две точки окружности.

Диаметр: хорда, проходящая через центр окружности. Диаметром окружности также называют длину этой хорды.

Пи ( ): Число 3, 141 592 653 589 793 . , равное отношению длины окружности к диаметру.

Радиус: отрезок, соединяющий центр окружности с какой-либо ее точкой (а так же длина этого отрезка).

Сектор круга: фигура, ограниченная двумя радиусами и дугой, на которую они опираются.

Касательная к окружности: прямая, перпендикулярная радиусу окружности, проведенная в точку касания.

Диаметр = 2 x радиус окружности

Длина окружности = x диаметр = 2 x радиус

Площадь круга :
площадь = r 2

Длина дуги окружности: (с центральным углом )
если выражен в градусах, то длина = x ( /180) x r
если выражен в радианах, то длина = r x

Площадь сектора окружности: (с центральным углом q )
если выражен в градусах, то площадь = ( /360) x r 2
если выражен в радианах, то площадь = ( /2) x r 2

Уравнение окружности: (в декартовых координатах)

для окружности с центром в точке (x₀, y ₀ ) и радиусом ( r ):

Уравнение окружности: (в полярных координатах)
для окружности с центром в точке (0, 0): r ( ) = радиус

для окружности с центром с полярными координатами: ( c , a ) и радиусом a :
r 2 — 2 cr cos ( — a ) + c 2 = a 2

Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Уравнение фигуры в декартовых координатах определение окружности вывод уравнения окружности

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:Построение кривой в полярной системе координатСкачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Please wait.

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

We are checking your browser. mathvox.ru

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Уравнение окружностиСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d9cf9133df15aa6 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Уравнение окружности

Уравнение окружности с центром в точке (a;b) и радиусом R в прямоугольной системе координат имеет вид

1. Пусть в прямоугольной системе координат задана окружность с центром в точке A (a;b) и радиусом R (R>0).

Чтобы составить уравнение этой окружности, выберем на окружности произвольную точку B (x;y).

По определению окружности, расстояние от центра до любой точки окружности равно радиусу R, то есть AB=R.

Так как B (x;y) — произвольная точка окружности, координаты любой точки окружности удовлетворяют этому уравнению.

2. Если пара чисел (x_o;y_o) удовлетворяет данному уравнению, то

А это значит, что расстояние между точками C(x_o;y_o) и A(a;b) равно R. Значит, точка C(x_o;y_o) принадлежит окружности с центром в точке A(a;b) и радиусом R.

Следовательно, данное уравнение фигуры является уравнением окружности.

🔥 Видео

9 Длина дуги числовой окружностиСкачать

Длина дуги окружности. Практическая часть. 9 класс.Скачать

Как искать точки на тригонометрической окружности.Скачать

ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать