ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
§ 2. Распространение звука
§ 3. Волновое уравнение
§ 4. Решения волнового уравнения
§ 5. Скорость звука
В этой главе мы будем обсуждать новое явление — волны. О волнах часто и много говорится в физике, и мы наше внимание должны сконцентрировать на этом вопросе не только потому, что собираемся рассмотреть частный пример волн — звук,— но и потому, что волновые процессы имеют и другие многочисленные применения во всех областях физики.
Изучая гармонический осциллятор, мы уже отмечали, что существуют примеры как механических колеблющихся систем, так и электрических. Волны тесно связаны с колебательными системами, однако волновое движение есть не только колебание в данном месте, зависящее от времени, но и движение в пространстве.
Мы уже на самом деле изучали волны. Когда мы говорили о волновых свойствах света, мы обращали особое внимание на пространственную интерференцию волн одной и той же частоты от различных источников, расположенных в разных местах. Существуют еще два важных явления, о которых мы не упоминали и которые свойственны как свету, т. е. электромагнитным волнам, так и любой другой форме волнового движения. Первое из них — это явление интерференции, но уже не в пространстве, а во времени. Когда мы слушаем звуки сразу от двух источников, причем частоты их слегка отличаются, к нам приходят то гребни обеих волн, то гребень одной волны и впадина другой (фиг. 47.1).
Фиг. 47.1. Интерференция звука во времени от двух источников с несколько отличающимися частотами приводит к биениям.
Звук то усиливается, то ослабевает, возникают биения, или, другими словами, происходит интерференция во времени. Второе явление — это волновое движение в замкнутом объеме, когда волны отражаются то от одной, то от другой стенки.
Все эти эффекты можно было, конечно, рассмотреть и на примере электромагнитных волн. Мы этого не сделали по той причине, что на одном примере мы не почувствовали бы общего характера явления, свойственного самым разным процессам. Чтобы подчеркнуть общность понятия волн вне рамок электродинамики, мы рассмотрим здесь другой пример — звуковые волны.
Есть еще пример — морские волны, набегающие на берег, или мелкая водяная рябь. Кроме того, существуют два рода упругих волн в твердых телах: волны сжатия (или продольные волны), в которых частицы тела колеблются вперед и назад в направлении распространения волны (звуковые колебания в газе именно такого типа), и поперечные волны, когда частицы тела колеблются перпендикулярно направлению движения волны. При землетрясениях в результате движения участка земной коры возникают упругие волны обоих типов.
И, наконец, есть еще один тип волн, который нам дает современная физика. Это волны, определяющие амплитуду вероятности нахождения частицы в данном месте,— «волны материи», о которых мы уже говорили. Их частота пропорциональна энергии, а волновое число пропорционально импульсу. Эти волны встречаются в квантовой механике.
В этой главе мы будем рассматривать только такие волны, скорость которых не зависит от длины волны. Пример таких волн — распространение света в вакууме. Скорость света в этом случае одна и та же для радиоволн, для синего и зеленого света и вообще для света любой длины волны. Именно поэтому, когда мы описывали волновые явления, мы сначала и не заметили самого факта распространения волн. Вместо этого мы говорили, что если перенести заряд в некоторую точку, то электрическое поле на расстоянии х будет пропорционально ускорению заряда, но не в момент времени t, а в более ранний момент времени t— x/c. Поэтому распределение электрического поля в пространстве в некоторый момент времени, изображенное на фиг. 47.2, спустя время t передвинется на расстояние ct. Выражаясь математически, можно сказать, что в рассматриваемом нами одномерном случае электрическое поле есть функция от x—ct. Отсюда видно, что при t=0 оно оказывается функцией только х. Если взять более поздний момент времени и несколько увеличить х, мы получим ту же самую величину поля. Например, если максимум поля возникает при x=3 и в момент времени t=0, то положение максимума в момент времени t находится из равенства
Мы видим, что такая функция отвечает распространению волны. Итак, функция f(x—ct) описывает волну. Мы можем все сказанное записать кратко так:
если Dx=cDt. Конечно, существует еще и другая возможность, когда источник излучает волны не направо, как указано на фиг. 47.2, а налево, так что волны будут двигаться в сторону отрицательных х.
Фиг. 47.2. Примерное распределение электрического поля в некоторый момент времени (а) и электрическое поле через промежуток времени t (b).
Тогда распространение волны описывалось бы функцией g(x+ct).
Может еще случиться, что в пространстве одновременно движется несколько волн, и тогда электрическое поле есть сумма всех полей и все они распространяются независимо. Это свойство электрических полей можно выразить так: пусть f1(x—ct) отвечает одной волне, a f2(x—ct) — другой, тогда их сумма также описывает некоторую волну. Это утверждение называется принципом суперпозиции. Он справедлив и для звуковых волн.
Мы хорошо знаем, что звуки воспринимаются в той последовательности, в какой они создаются источником. А если бы высокие частоты распространялись быстрее, чем низкие, то вместо звуков музыки мы слышали бы резкий и отрывистый шум. Точно так же если бы красный свет двигался быстрее, чем синий, то вспышка белого света выглядела бы сначала красной, затем белой и наконец синей. Мы хорошо знаем, что такого на самом деле не происходит. И звук, и свет движутся в воздухе со скоростью, почти не зависящей от частоты. Примеры волнового движения, где этот принцип не выполняется, будут рассмотрены в гл. 48.
Для света (электромагнитных волн) мы получили формулу, определяющую электрическое поле в данной точке, которое возникает при ускорении заряда. Казалось бы, нам остается теперь подобным образом определить какую-нибудь характеристику воздуха, скажем давление на заданном расстоянии от источника через движение источника, и учесть запаздывание при распространении звука.
В случае света такой подход был приемлем, так как все наши знания сводились к тому, что заряд в одном месте действует с некоторой силой на заряд в другом месте. Подробности распространения взаимодействия из одной точки в другую были абсолютно несущественны. Но звук, как известно, распространяется по воздуху от источника к уху, и естественно спросить, чему равно давление воздуха в каждый данный момент. Кроме того, хотелось бы знать, как именно движется воздух.
В случае электричества мы могли поверить в правило, поскольку законы электричества мы еще не проходили, но для звука это не так. Нам недостаточно сформулировать закон, определяющий распространение звукового давления в воздухе; этот процесс должен быть объяснен на основе законов механики. Короче, звук есть часть механики, и он должен быть объяснен с помощью законов Ньютона. Распространение звука из одной точки в другую есть просто следствие механики и свойств газов, если звук распространяется в газе, или свойств жидкостей и твердых тел, если звук проходит через эти среды. Позднее мы выведем также свойства света и его волновое движение из законов электродинамики.
§ 2. Распространение звука
Давайте выведем теперь свойства распространения звука между источником и приемником, основываясь на законах Ньютона, но не учитывая при этом взаимодействия звука с источником и приемником. Обычно мы более подробно останавливались на результате, а не на его выводе. В этой главе мы используем противоположный подход. Главным здесь будет в некотором смысле само получение результата. Метод объяснения новых явлений с помощью старых, законы которых уже известны, представляет собой, пожалуй, величайшее искусство математической физики. Математическая физика решает две проблемы: найти решение заданного уравнения и найти уравнения, описывающие новое явление. То, чем мы будем заниматься, относится как раз ко второй проблеме.
Рассмотрим простейший пример — распространение звука в одномерном пространстве. Для вывода нам сначала необходимо понять, что же в действительности происходит. В основе явления лежит следующий факт: когда тело перемещается в воздухе, возникает возмущение, которое как-то распространяется по воздуху. На вопрос, что это за возмущение, мы можем ответить: это такое движение тела, которое вызывает изменение давления. Конечно, если тело движется медленно, воздух лишь обтекает его, но нас интересует быстрое движение, когда воздух не успевает обойти вокруг тела. При этих условиях воздух в процессе движения сжимается и возникает избыточное давление, толкающее окружающие слои воздуха. Эти слои в свою очередь сжимаются, снова возникает избыточное давление, и вот начинает распространяться волна.
Опишем этот процесс на языке формул. Прежде всего решим, какие нам нужны переменные. В нашей задаче нам нужно знать, насколько переместился воздух, поэтому смещение воздуха в звуковой волне, несомненно, будет первой нашей переменной. Вдобавок хотелось бы знать, как меняется плотность воздуха при смещении. Давление воздуха тоже меняется, и это еще одна интересная переменная. Кроме того, воздух движется с некоторой скоростью, и мы должны уметь определить скорость частиц воздуха. Частицы воздуха имеют еще и ускорение, но, записав все эти переменные, мы сразу же поймем, что и скорость, и ускорение будут нам известны, если известно смещение воздуха как функция времени.
Как уже говорилось, мы рассмотрим волну в одном измерении. Так можно поступить, если мы находимся достаточно далеко от источника и так называемый фронт волны мало отличается от плоскости. На этом примере наше доказательство будет проще, поскольку можно сказать, что смещение c зависит только от х и t, а не от у и z. Поэтому поведение воздуха описывается функцией c (х, t).
Насколько полно такое описание? Казалось бы, оно очень не полно, потому что нам не известны подробности движения молекул воздуха. Они движутся во всех направлениях, и этот факт не отражается функцией c(х, t). С точки зрения кинетической теории, если в одном месте наблюдается большая плотность молекул, а в соседнем меньшая, молекулы будут переходить из области с большей плотностью в область с меньшей плотностью, так чтобы уравнять плотности. Очевидно, что при этом никаких колебаний не происходит и звук не возникает. Для получения звуковой волны нужно, чтобы молекулы, вылетая из области с большей плотностью и давлением, переда-пали импульс другим молекулам, находящимся в области разрежения. Звук возникает в том случае, если размеры области изменения плотности и давления намного больше расстояния, проходимого молекулами до соударения с другими молекулами. Это расстояние есть длина свободного пробега, и оно должно быть много меньше расстояния между гребнями и впадинами давления. В противном случае молекулы перейдут из гребня во впадину, и волна моментально выровняется.
Мы, естественно, хотим описать поведение газа в масштабе, большем, чем длина свободного пробега, так что свойства газа не будут определяться поведением отдельных молекул. Например, смещение есть смещение центра инерции небольшого объема газа, а давление или плотность относятся к этому же объему. Мы обозначим давление через Р, а плотность через r, причем обе величины будут функциями от х и t. Необходимо помнить, что наше описание приближенное и справедливо лишь, когда свойства газа не слишком быстро меняются с расстоянием.
§ 3. Волновое уравнение
Итак, физические явления, происходящие в звуковой волне, обладают следующими тремя свойствами:
I. Газ движется, и плотность его меняется. II. При изменении плотности меняется и давление. III. Неравномерное распределение давления вызывает движение газа.
Рассмотрим сначала свойство П. Для любого газа, жидкости или твердого тела давление является функцией плотности. До прихода звуковой волны мы имели равновесное состояние с давлением Р0 и плотностью r. Давление Р зависит от плотности среды: Р=f(r), и в частности равновесное давление Р0=f(r0). Отклонения величины давления от равновесного в звуковой волне очень малы. Давление удобно измерять в барах (1 бар=105н/м2). Давление в одну стандартную атмосферу приблизительно равно 1 бар (1 атм=1,0133 бар). Для звука обычно используется логарифмическая шкала интенсивности, так как восприятие уха, грубо говоря, растет логарифмически. В этой децибельной шкале уровень звукового давления I связан с амплитудой звукового давления:
где давление отнесено к некоторому стандартному давлению Ротн=2•10-10 бар.
Звуковое давление Р=103 Ротн=2•10-7 бар соответствует довольно сильному звуку в 60 дб. Мы видим, что давление меняется в звуковой волне на очень малую величину по сравнению с равновесным или средним, равным 1 атм. Смещение и перепады плотности также очень малы. При взрывах, однако, изменения уже не столь малы; избыточное звуковое давление может превышать 1 атм. Такие большие перепады давления приводят к новым явлениям, которые мы рассмотрим позже. В звуковых волнах уровень силы звука выше 100 дб встречается редко; уровень силы звука в 120 дб уже вызывает боль в ушах. Поэтому, написав для звуковой волны
Р=Р0+Рu, r = r0+ru, (47.2)
можно считать, что изменение давления Pu очень мало по сравнению с P0, а изменение плотности ru очень мало по сравнению с r0. Тогда
где P0 = f(r0) и f'(r0) — производная от f(r), взятая при значении r =r0. Второе равенство здесь возможно только потому, что ru очень мало. Таким образом, мы находим, что избыточное давление Pu пропорционально избыточной плотности ru; коэффициент пропорциональности обозначается через к:
(II) Рu=cru, где c=f'(r0)=(dP/dr
Это весьма простое соотношение и составляет точное содержание свойства II.
Перейдем теперь к свойству I. Предположим, что положение элемента объема воздуха, не возмущенного звуковой волной, есть х, а звук смещает его в момент времени t на величину c(х,t), так что его новое положение есть x+c(x, t), как показано на фиг. 47.3.
Далее, положение соседнего элемента объема есть х+Dх, и его смещенное положение есть х+Dх+c(х+Dх,t). Теперь можно найти изменение плотности. Поскольку мы рассматриваем плоскую волну, удобно взять единичную площадку, перпендикулярную оси х, т. е. направлению распространения волны. Количество воздуха, приходящееся на единичную площадку в интервале Dx, есть r0Dx, где r0 — невозмущенная, или равновесная, плотность воздуха. Эта порция воздуха, смещенная звуковой волной, будет находиться теперь между x+c (x,t) и x+Dх+c (х+Dх,t), причем количество воздуха в этом интервале то же самое, что в интервале Dx до прихода волны. Если через r обозначить новую плотность, то
Поскольку Dx мало, можно написать c (x+Dx,t)-c (x, t)=(дc/дx)Dx. Здесь уже появляется частная производная, потому что c зависит и от x, и от времени. Наше уравнение принимает вид
Но в звуковой волне все изменения малы, так что ru мало, c мало и дc/дх тоже мало. Поэтому в уравнении, которое мы только что написали,
можно пренебречь ru(дc/дх) по сравнению с r0(дc/дх). Так мы приходим к соотношению, которое требовалось согласно свойству I:
Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных х, плотность будет изменяться. Знак тоже правильный: если смещение c растет с ростом х, так что воздух расширяется, плотность должна уменьшаться.
Теперь нам нужно найти третье уравнение — уравнение движения, производимого избытком давления. Зная соотношение между силой и давлением, можно получить уравнение движения. Возьмем объем воздуха толщиной Dx и с единичной площадью грани, перпендикулярной х, тогда масса воздуха в этом объеме есть r0Dx, а ускорение воздуха есть д2c/дt2, так что масса, умноженная на ускорение для этого слоя, есть r0Dx(д2c/дt2). (Если Dx; мало, то безразлично, где брать ускорение — на краю слоя или где-нибудь посредине.) Сила, действующая на единичную площадку нашего слоя, перпендикулярную оси x, должна быть равна r0Dx(д2хc/дt2). В точке х мы имеем силу Р(х,t), действующую на единицу площади в направлении +х, а в точке x+Dx; возникает сила в обратном направлении, по величине равная Р(x;+ Dx, t) (фиг. 47.4):
Фиг. 47.4. Результирующая сила в направлении оси х, возникающая за счет давления на единичную площадку, перпендикулярную к оси х, есть — (дР/дх)Dх.
Мы учли, что Dx; мало и что только избыточное давление Ри меняется в зависимости от х. Итак, согласно свойству III мы получаем
Теперь уже уравнений достаточно, чтобы увязать все величины и привести к одной переменной, скажем х. Можно выразить Рu в (47.11) с помощью (47.4):
а затем исключить ru с помощью (I). Тогда r0 сократится и у нас останется
Обозначим с2s =x, тогда можно написать
Это и есть волновое уравнение, которое описывает распространение звука в среде.
§ 4. Решения волнового уравнения
Посмотрим теперь, действительно ли волновое уравнение описывает основные свойства звуковых волн в среде. Прежде всего мы хотим вывести, что звуковое колебание, или возмущение, движется с постоянной скоростью. Кроме того, нам нужно доказать, что два различных колебания могут свободно проходить друг через друга, т. е. принцип суперпозиции. Мы хотим еще доказать, что звук может распространяться и вправо и влево. Все эти свойства должны содержаться в нашем одном уравнении.

Раньше мы отмечали, что любое возмущение, имеющее вид плоской волны и движущееся с постоянной скоростью, записывается в виде f(x—vt). Посмотрим теперь, является ли f(x—vt) решением волнового уравнения. Вычисляя дc/дх, получаем производную функции dcldx=f‘(x—vt). Дифференцируя еще раз, находим

Дифференцируя эту же функцию c по t, получаем значение — V, умноженное на производную, или дc/dt=-vf (x—vt); вторая производная по времени дает
Очевидно, что f(х-vt) удовлетворяет волновому уравнению, если v равно cs.
Таким образом, из законов механики мы получаем, что любое звуковое возмущение распространяется со скоростью cs и, кроме того,
тем самым мы связали скорость звуковых волн со свойствами среды.
Легко увидеть, что звуковая волна может распространяться: и в направлении отрицательных х, т. е. звуковое возмущений вида c (х, t)=g(x+vt) также удовлетворяет волновому уравнению. Единственное отличие этой волны от той, которая распространялась слева направо, заключается в знаке v, но знак д2c/dt2 не зависит от выбора x+vt или х-vt, потому что в эту производную входит только v2. Отсюда следует, что решение уравнения описывает волны, бегущие в любом направлении со скоростью cs.
Особый интерес представляет вопрос о суперпозиции решений. Допустим, мы нашли одно решение, скажем c1 . Это значит, что вторая производная 3d по х равна второй производной c1 по t1, умноженной на 1/с2s. И пусть есть второе решение c2, обладающее тем же свойством. Сложим эти два решения, тогда получается

Теперь мы хотим удостовериться, что c (х, t) тоже представляет некую волну, т. е. c тоже удовлетворяет волновому уравнению. Это очень просто доказать, так как

и вдобавок
Отсюда следует, что d2c/dx2=(l/c2s)д2c/dt2, так что справедливость принципа суперпозиции проверена. Само существование принципа суперпозиции связано с тем, что волновое уравнение линейно по c.

Теперь естественно было бы ожидать, что плоская световая волна, распространяющаяся вдоль оси х и поляризованная так, что электрическое поле направлено по оси y, тоже удовлетворяет волновому уравнению
где с — скорость света. Волновое уравнение для световой волны есть одно из следствий уравнений Максвелла. Уравнения электродинамики приводят к волновому уравнению для света точно так же, как уравнения механики приводят к волновому уравнению для звука.
§ 5. Скорость звука
При выводе волнового уравнения для звука мы получили формулу, которая связывает при нормальном давлении скорость движения волны и относительное изменение давления с плотностью: с2s=(dP/dr)0. (47.21) Чтобы оценить скорость изменения давления, очень важно знать, как при этом меняется температура. Можно ожидать, что в местах сгущения звуковой волны температура повысится, а в местах разрежения — понизится. Ньютон первым вычислил скорость изменения давления с плотностью, предположив, что температура при этом не меняется. Он считал, что тепло передается из одной области звуковой волны в другую так быстро, что температура измениться не успеет. Способ Ньютона дает изотермическую скорость звука, что неправильно. Правильное вычисление было сделано позже Лапласом, считавшим вопреки Ньютону, что давление и температура в звуковой волне меняются адиабатически. Поток тепла из области сгущения в область разрежения пренебрежимо мал, если только длина волны велика по сравнению с длиной свободного пробега. При этих условиях ничтожная утечка тепла в звуковой волне не влияет на скорость звука, хотя и приводит к небольшому поглощению звуковой энергии. Мы можем, естественно, ожидать, что поглощение тепла усилится, когда длина волны приблизится к длине свободного пробега, но такие длины волн примерно в миллион раз меньше длины волны слышимого звука.
Итак, для звука истинная скорость изменения давления с плотностью должна вычисляться без учета отвода тепла. Это соответствует адиабатическому изменению давления, для которого мы нашли, что PVg=const, где V — объем. Поскольку плотность r обратно пропорциональна объему, связь P и r для адиабатических процессов дается соотношением
откуда мы получаем dP/dr=gP/r. Тогда для скорости звука возникает соотношение
Можно еще написать с2s= gPV/rV и использовать соотношение PV=NkT. Мы видим, кроме того, что rV есть масса газа, которую можно записать как Nm или m, где m — масса молекулы, а m — молекулярный вес. Таким образом, находим
откуда видно, что скорость звука зависит только от температуры газа и не зависит от давления или плотности. Мы уже отмечали, что

где — средняя квадратичная скорость молекул. Отсюда следует, что с2s=g/3 , или
Это равенство означает, что скорость звука есть средняя скорость молекул воздуха (точнее, корень квадратный из средней квадратичной скорости), умноженная на некоторое число, грубо говоря, на 1/(3)1/2. Другими словами, она того же порядка величины, что и скорость молекул, но на самом деле несколько меньше средней скорости молекул.
В общем-то мы могли этого ожидать, потому что такое возмущение, как изменение плотности, передается в конечном счете движением молекул. Однако подобного рода соображения не подсказывают нам точного значения скорости; могло ведь оказаться, что звук переносится самыми быстрыми или самыми медленными молекулами. Разумно и весьма утешительно, что скорость звука оказалась равной приблизительно половине средней молекулярной скорости.
* При таком выборе Pотн Р — уже не максимальная амплитуда звукового давления, а «среднее квадратичное» давление, равное максимальному, деленному на 1/Ö2.
Видео:Что такое скорость звука и как он распространяется?Скачать

Скорость звука. Отражение звука. Эхо (Ерюткин Е.С.)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Тема сегодняшнего видеоурока – «Скорость звука, отражение звука, его эхо». На нём мы поговорим о распространении звука в воздухе, дадим определение этому понятию, узнаем, от чего зависит скорость звука, методы его измерения. Также узнаем, как создаётся отражённая звуковая волна и как мы можем услышать эхо.
Видео:Физика 9 класс (Урок№15 - Звуковые волны. Скорость звука.)Скачать

Уравнение для скорости распространения звука
Перед тем, как приступить к рассмотрению темы, дадим определение такому явлению, как звук.
Звук или звуковые волны – это волны, которые способно воспринять человеческое ухо.
При этом звуковые частоты имеют диапазон: примерно от 20 Г ц до 20 к Г ц .
Инфразвук – звуковые волны, имеющие частоту менее 20 Г ц .
Ультразвук – волны звука, имеющие частоту более 20 к Г ц .
Волнам звукового диапазона свойственно распространяться как в газе, так и в жидкости (продольные волны), и в твердом теле (продольные и поперечные волны). Особенно интересно для науки заниматься изучением распространения звуковых волн в газообразной среде, что по сути есть среда нашего обитания.
Акустика – это направление физики, занимающееся изучением звуковых явлений.
Когда звук получает распространение в газе, атомы и молекулы испытывают колебания вдоль направления распространения волны, следствием чего становится изменение локальной плотности ρ и давления p .
Звуковые волны в газе зачастую называют волнами плотности или волнами давления.
В случае простых гармонических звуковых волн, получающих распространение вдоль оси O X , изменение давления p ( x , t ) имеет зависимость от координаты x и времени t , которая записывается так:
p ( x , t ) = p 0 cos ω t ± k x .
В аргументе косинуса мы видим два противоположных знака, что имеет отношение к двум направлениям распространения волны. Запишем выражение, которое покажет соотношение таких величин, как круговая частота ω , волновое число k , длина волны λ , скорость звука υ (соотношение будет таким же, как применимо для поперечных волн в струне или резиновом жгуте):
υ = λ T = ω k ; k = 2 π λ ; ω = 2 π f = 2 π T .
Одной из ключевых характеристик звука является скорость распространения.
Скорость распространения – величина, описывающая звуковую волну, задаваемая инертными и упругими свойствами среды и определяемая для продольных волн в любой однородной среде при помощи формулы:
В указанной формуле B является модулем всестороннего сжатия, ρ – средней плотностью среды.
Видео:Распространение звука. Звуковые волны | Физика 9 класс #32 | ИнфоурокСкачать

Формула Лапласа
Первые попытки рассчитать значение скорости звука предпринял Ньютон, предположив равенство упругости воздуха атмосферному давлению p а т м . В таком случае значение скорости звука в воздушной среде – менее 300 м / с , в то время как истинная скорость звука при нормальных условиях (температура 0 ° С и давление 1 а т м ) равна 331 , 5 м / с , а скорость звука при температуре 20 ° С и давлении 1 а т м составит 343 м / с . Лишь по прошествии более ста лет было показано, почему предположение Ньютона не выполняется. Французский физик П. Лаплас указал, что ньютоновское видение равносильно предположению о быстром выравнивании температуры между областями разрежения и сжатия, и невыполнение его связано с плохой теплопроводностью воздуха и малым периодом колебаний в звуковой волне. В действительности между областями разрежения и сжатия газа появляется разность температур, существенным образом влияющая на упругие свойства. Лаплас, в свою очередь, выдвинул предположение, что сжатие и разрежение газа в звуковой волне происходят в соответствии с адиабатическим законом: в отсутствии влияния теплопроводности. В 1816 году физик вывел формулу, предназначенную для расчета скорости звуковой волны в воздухе и получившей название формулы Лапласа.
Формула Лапласа для определения скорости звука имеет запись:
Где p является значением среднего давления в газе, ρ – средней плотности, а γ есть некоторая константа, находящаяся в зависимости от свойств газа.
В нормальных условиях скорость звука, рассчитанная по формуле Лапласа, равна υ = 332 м / с .
В термодинамике имеется доказательство, что константа γ представляет собой отношение теплоемкостей при постоянном давлении C p и постоянном объеме C V .
Формула Лапласа может быть записана несколько иначе, если использовать уравнение состояния идеального газа. Таким образом, окончательный вид формулы для определения скорости звука будет такой:
В данной формуле T – абсолютная температура, M – молярная масса,
R = 8 , 314 Д ж / м о л ь · К – универсальная газовая постоянная. Скорость звука находится в сильной зависимости от свойств газа: скорость звука тем больше, чем легче газ, в котором звуковая волна получает распространение.
Для наглядности приведем некоторые примеры.
Когда звук распространяется в воздушной среде ( M = 29 · 10 – 3 к г / м о л ь ) при нормальных условиях: υ = 331 , 5 м / с ;
Когда звук распространяется в гелии ( M = 4 · 10 – 3 к г / м о л ь ) : υ = 970 м / с ;
Когда звук распространяется в водороде ( M = 2 · 10 – 3 к г / м о л ь ) : υ = 1270 м / с .
В жидкостях и твердых телах скорость звуковых волн еще больше. В воде, например, υ = 1480 м / с (при 20 ° С ), в стали υ = 5 – 6 к м / с .
Видео:Урок 95 (осн). Механические волны. ЗвукСкачать

Характеристики звуковых волн
Помимо скорости распространения звук имеет и другие характеристики, связанные с восприятием его человеческими органами слуха.
Громкость звука
Рассуждая о том, как человеческое ухо воспринимает звук, в первую очередь мы говорим об уровне громкости, который зависит от потока энергии или интенсивности звуковой волны. А то, как воздействует звуковая волна на барабанную перепонку, зависит от звукового давления.
Звуковое давление – это амплитуда p 0 колебаний давления в волне
Природа отлично потрудилась, создавая такое совершенное устройство, как человеческое ухо: оно способно воспринимать звуки в обширнейшем диапазоне интенсивностей. Мы имеем возможность слышать как слабый писк комара, так и грохот вулкана.
Порог слышимости – минимальное значение величины звукового давления, при котором звук этой частоты еще воспринимается человеческим ухом.
Болевой порог – это верхняя граница диапазона слышимости человека; та величина звукового давления, при котором звук вызывает в человеческом ухе ощущение боли.
Порог слышимости представляет собой значение p 0 около 10 – 10 а т м , т. е. 10 – 5 П а : такой слабый звук характеризуется колебанием молекул воздуха в волне звука с амплитудой всего лишь 10 – 7 с м ! Болевой же порог соответствует значению p 0 порядка 10 – 4 а т м или 10 П а . Т.е., человеческое ухо способно к восприятию волн, в которых звуковое давление изменяется в миллион раз. Поскольку интенсивность звука пропорциональна квадрату звукового давления, диапазон интенсивностей оказывается порядка 10 12 !
Человеческое ухо, восприимчивое к звукам такого огромного диапазона интенсивности, допустимо сравнить с прибором, которым возможно измерить как диаметр атома, так и размеры футбольного поля.
Для общей информированности заметим, что обычным разговорам людей в комнате соответствует интенсивность звука, примерно в 10 6 раз превышающая порог слышимости, а интенсивность звука на рок-концерте находится очень близко к болевому порогу.
Высота звука
Высота звуковой волны – еще одна характеристика звука, влияющая на слуховое восприятие. Человеческие ухо воспринимает колебания в гармонической звуковой волне как музыкальный тон.
Высокий тон – это звуки с колебаниями высокой частоты.
Низкий тон – это звуки с колебаниями низкой частоты.
Звуки, которые издают музыкальные инструменты, а также звуки голоса человека значимо отличаются друг от друга по высоте тона и по диапазону частот.
К примеру, диапазон наиболее низкого мужского голоса – баса – находится в пределах примерно от
80 до 400 Г ц , а диапазон высокого женского голоса – сопрано – от 250 до 1050 Г ц .
Октава – это диапазон колебаний звука, который соответствует изменению частоты колебаний в 2 раза.
Скрипка, к примеру, звучит в диапазоне примерно трех с половиной октав ( 196 – 2340 Г ц ) ,
а пианино – семи с лишним октав ( 27 , 5 – 4186 Г ц ) .
Говоря о частоте звука, который извлекается при помощи струн любого струнного музыкального инструмента, будем иметь в виду частоту f 1 основного тона. Однако колебания струн содержат также гармоники, частоты f n которых отвечают соотношению:
f n = n f 1 , ( n = 1 , 2 , 3 , . . . ) .
Таким образом, звучащая струна способна излучать целый спектр волн с кратными частотами. Амплитуды A n этих волн имеют зависимость от способа возбуждения струны, будь то смычок или молоточек. Эти амплитуды необходимы для придания музыкальной окраски звуку (тембру).
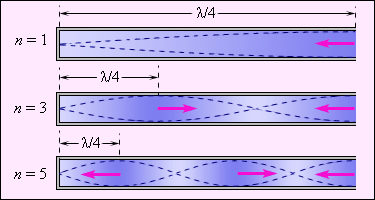
Аналогичный процесс мы наблюдаем, когда звучат духовые музыкальные инструменте. Трубы духовых инструментов служат акустическими резонаторами – акустическими колебательными системами, имеющими способность возбуждаться (резонировать) от звуковых волн определенных частот. Определенные же условия способствуют возникновению внутри трубы стоячей звуковой волны. Рисунок 2 . 7 . 1 демонстрирует несколько видов стоячих волн (мод) в органной трубе, закрытой с одного конца и открытой с другого. Звучание духовых инструментов, так же, как и струнных, состоит из целого спектра волн с кратными частотами.
Рисунок 2 . 7 . 1 . Стоячие волны в трубе органа (закрыта лишь с одной стороны). Стрелки указывают направления движения частиц воздуха за один полупериод колебаний.
Музыкальные инструменты необходимо периодически настраивать.
Камертон – устройство для настройки музыкальных инструментов, состоящее из настроенных в резонанс деревянного акустического резонатора и соединенной с ним металлической вилки.
Удар молоточка по вилке вызывает возбуждение всей системы камертона с последующим звучанием чистого музыкального тона.
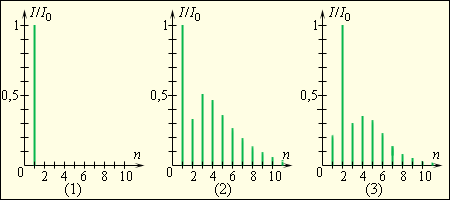
Гортань певца – по сути тоже акустический резонатор. Рисунок 2 . 7 . 2 демонстрирует спектры звуковых волн, издаваемых камертоном, струной пианино и низким женским голосом (альтом), звучащими на одной и той же ноте.
Рисунок 2 . 7 . 2 . Относительные интенсивности гармоник в спектре волну звука при звучании камертона ( 1 ) , пианино ( 2 ) и низкого женского голоса (альт) ( 3 ) на ноте «ля» контроктавы ( f 1 = 220 Г ц ) . По оси ординат отложены относительные интенсивности I I 0 .
Звуковые волны, чьи частотные спектры показаны на рисунке 2 . 7 . 2 , имеют одну и ту же высоту, но различные тембры.
Видео:Определение скорости распространения звука в воздухеСкачать

Биения
Разберем также такое явление, как биения.
Биение – это явление, возникающее, когда две гармонические волны с близкими, но все же имеющими отличия частотами, накладываются друг на друга.
Биения сопровождают, к примеру, одновременное звучание двух струн, имеющих настройки практически одинаковой частоты. Человеческий орган слуха воспринимает биения как гармонический тон с громкостью, периодически изменяющейся во времени. Запишем выражения, показывающие закономерность изменения звуковых давлений p 1 и p 2 , которые осуществляют воздействие на ухо:
p 1 = A 0 cos ω 1 t и p 2 = A 0 cos ω 2 t .
Для удобства примем, что амплитуды колебаний звуковых давлений являются одинаковыми и равны p 0 = A 0 0.
Согласно принципу суперпозиции полное давление, которое вызывается обеими волнами в каждый момент времени, есть совокупность звуковых давлений, задаваемых каждой волной в тот же момент времени. Запишем выражение, показывающее суммарное воздействие волн, используя тригонометрические преобразования:
p = p 1 + p 2 = 2 A 0 cos ω 1 — ω 2 2 t cos ω 1 + ω 2 2 t = 2 A 0 cos 1 2 ∆ ω t cos ω с р t ,
где ∆ ω = ω 1 — ω 2 , а ω с р = ω 1 + ω 2 2 .
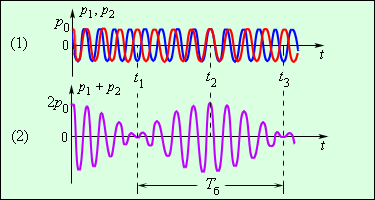
Рисунок 2 . 7 . 3 ( 1 ) отображает, каким образом давления p 1 и p 2 зависимы от времени t . В момент времени t = 0 оба колебания находятся в фазе, и их амплитуды суммируются. Поскольку частоты колебаний имеют хоть и небольшие, но отличия, через некоторое время t 1 колебания войдут в противофазу. В этот момент суммарная амплитуда станет равна нулю: колебания взаимно «погасятся». К моменту времени t 2 = 2 t 1 колебания вновь окажутся в фазе и т. д. (рисунок 2 . 7 . 3 ( 2 ) ).
Период биений Т б – это минимальное значение интервала между двумя моментами времени, которым соответствуют максимальная и минимальная амплитуда колебаний.
Формула, которая определяет медленно изменяющуюся амплитуду A результирующего колебания, имеет запись:
A = 2 A 0 cos 1 2 ∆ ω t .
Период Т б изменения амплитуды равен 2 π Δ ω . Мы можем это продемонстрировать, приняв следующее предположение: периоды колебаний давлений в звуковых волнах T 1 и T 2 являются такими, что T 1 T 2 (т. е. ω 1 > ω 2 ). За период биений Т б наблюдается некоторое число n полных циклов колебаний первой волны и ( n – 1 ) циклов колебаний второй волны:
T б = n T 1 = ( n — 1 ) T 2 .
T б = T 1 T 2 T 2 — T 1 = 2 π ω 1 — ω 2 = 2 π ∆ ω или f б = 1 T б = 1 T 1 — 1 T 2 = f 1 — f 2 = ∆ f .
f б есть частота биений, определяемая как разность частот Δ f двух звуковых волн, которые воспринимаются ухом одновременно.
Органы слуха человека способны к восприятию звуковых биений до частот 5 – 10 Г ц . Прослушивание биений – это важный элемент техники настройки музыкальных инструментов.
Рисунок 2 . 7 . 3 . Биения, возникающие, когда накладываются две звуковые волны с близкими частотами.
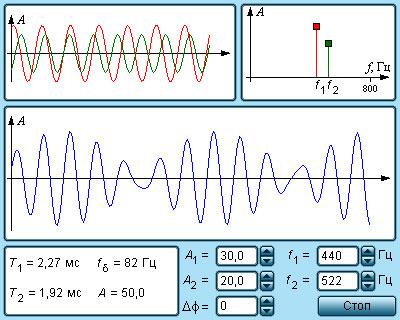
Рисунок 2 . 7 . 4 . Модель явления биений.
🎦 Видео
Распространение звука в различных средахСкачать

Урок 378. Методы определения скорости звука в воздухеСкачать

Физика 9 класс. §32 Распространение звука. Звуковые волны.Скачать

Волны. Основные понятия. Решение задач.Задача 1Скачать

Физика 11 класс (Урок№2 - Механические волны.)Скачать

Скорость звукаСкачать

Урок 372. Скорость продольной волны в стержне. Скорость звука в жидкостях и газах.Скачать

Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать

Скорость звукаСкачать

Опыты по физике. Измерение скорости звукаСкачать

Урок 371. Фазовая скорость волны. Скорость поперечной волны в струнеСкачать

Визуализация скорости света и скорости звукаСкачать

Длина волны. Скорость распространения волн | Физика 9 класс #29 | ИнфоурокСкачать

Звук, характеристики звука, акустический резонанс, эхо. Практическая часть - решение задачи.9 класс.Скачать

Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать