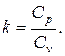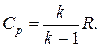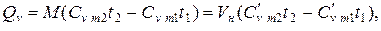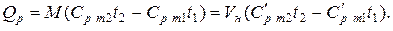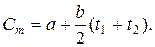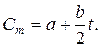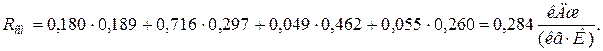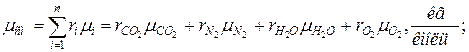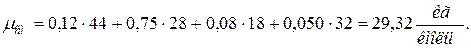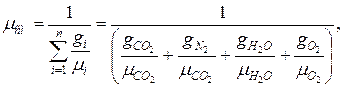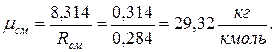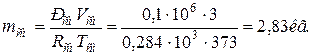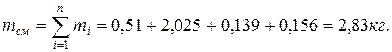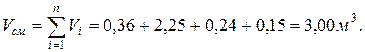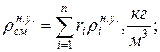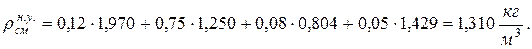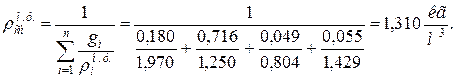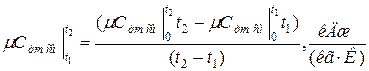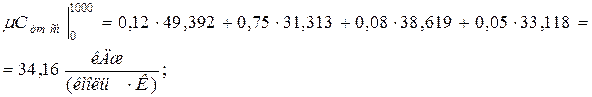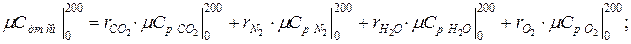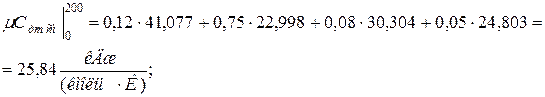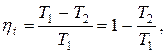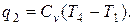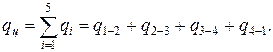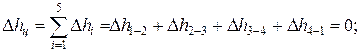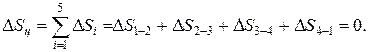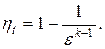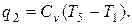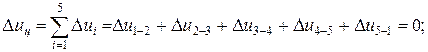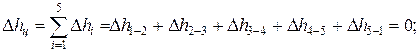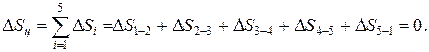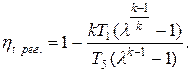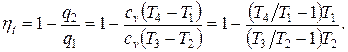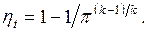Теплоемкостью (С) называют отношение количества теплоты, необходимой для изменения температуры в веществе на бесконечно малую величину:
Такую теплоемкость называют истинной.
При решении практических задач используют среднюю теплоемкость — условную постоянную величину в определенном интервале температур:
В зависимости от единиц количества вещества различают:
- • массовую теплоемкость с, кДж/(кг • К);
- • молярную теплоемкость рс или См, кДжДкмоль-К);
• объемную теплоемкость С или с’, отнесенную к 1 м 3 газа при нормальных физических условиях (j) = 760 мм рт. ст., t = 0°С), кДж/(м 3 • К) .
Массовая, молярная и объемная теплоемкости связаны между собой следующими зависимостями:
где |i — молекулярная масса вещества, кг/кмоль; vH, рн — удельный объем и плотность вещества при нормальных условиях; 22,4 м 3 /кмоль — объем одного киломоля любого идеального газа при нормальных физических условиях [1] .
Теплоемкость рабочего тела зависит от характера процесса, поэтому тоже является функцией процесса. В различных процессах теплоемкость может принимать значения в пределах -©о .
При анализе термодинамических процессов, протекающих при постоянном объеме (изохорных), используют изохорную теплоемкость cv, icv, c‘v, при анализе термодинамических процессов, протекающих при постоянном давлении (изобарных), используют изобарную теплоемкость ср, хср, с’р.
Используя выражения первого начала термодинамики, запишем:
Поскольку внутренняя энергия и энтальпия идеального газа зависят только от температуры, то их изменения в любом процессе можно рассчитать по формулам:
Связь между изобарной и изохорной теплоемкостями можно установить следующим образом. В изобарном процессе подведенная qp теплота расходуется на изменение внутренней энергии и на совершение внешней работы, а в изохорном — теплота qv расходуется только на изменение внутренней энергии. При нагревании 1 кг рабочего тела на одинаковую температуру разность между теплотой qp и qv будет равна работе, произведенной в процессе при р = const, т.е.
Для идеального газа работа в изобарном процессе может быть определена из уравнения состояния после дифференцирования последнего:
После подстановки значений (к]р и с1дг, и сокращения на с1Т получаем
Формула (1.27), устанавливающая связь между изобарной и изохорной теплоемкостями, называется уравнением Майера. Из нее вытекает также физический смысл газовой постоянной: газовая постоянная Я равна работе 1 кг газа в изобарном процессе при изменении его температуры на один кельвин (1 К). Разные газы в изобарном процессе производят неодинаковую работу.
Умножая обе части равенства (1.27) на молекулярную массу, получаем
Величина хЯ (или /?м) называется универсальной газовой постоянной. Из (1.28) следует, что разность молярных изобарной и изохорной теплоемкостей для идеальных газов является величиной постоянной.
При решении теплотехнических задач необходимо знать значения теплоемкостей различных газов. При невысоких температурах можно пользоваться значениями теплоемкостей, полученными на основе класси- ческой молекулярно-кинетической теории газов, согласно которой теплоемкость идеального газа зависит только от количества атомов в молекуле газа, характера процесса и не зависит от температуры.
Мольные теплоемкости идеальных газов в процессе, протекающем при постоянном объеме, имеют следующие значения: рсГ = 12,6 кДжДкмоль • К) — одноатомные газы; рс?1= 20,9 кДжДкмоль • К) — двухатомные газы; цс1)= 29 кДжДкмоль • К) — трех- и многоатомные газы.
Мольная изобарная теплоемкость может быть рассчитана но формуле (1.28). Массовые и объемные теплоемкости идеальных газов определяют по (1.21) и (1.22).
Сравнивая приведенные значения теплоемкости с опытными данными, можно прийти к следующим выводам. Если для одноатомных газов приведенные значения теплоемкостей хорошо совпадают с опытными результатами, то для двухатомных газов такое совпадение наблюдается только при температурах 0—20°С. При более высоких температурах имеют место значительные расхождения в величинах теплоемкостей.
Для трех- и многоатомных газов значения теплоемкости, полученные на основании молекулярно-кинетической теории газов, даже при невысоких температурах резко отличаются от величин теплоемкости, определяемой опытным путем. Эти расхождения объясняются тем, что классическая молекулярно-кинетическая теория газов не учитывает внутреннюю энергию колебательного движения атомов внутри молекулы. Влияние ее на величину теплоемкости тем сильнее, чем больше число атомов в молекуле и выше температура. Так, например, теплоемкость воздуха при 300°С по сравнению с теплоемкостью при 0°С увеличивается на 4%, а при 2000°С — почти на 25%. Еще больше увеличивается теплоемкость с повышением температуры у трехатомных газов.
В тепловых двигателях происходит значительное изменение температуры газа, поэтому необходимо учитывать зависимость теплоемкости от температуры:
Эту зависимость находят экспериментальным путем, она имеет вид алгебраического многочлена:
где а, /?, сI — коэффициенты, определяемые опытным путем.
Как следует из (1.29) и рис. 1.1, в общем случае теплоемкость имеет криволинейную зависимость от температуры. Величины истинных и средних изохорных и изобарных теплоемкостей в зависимости от температуры приводятся в справочных таблицах. В них средние значения теплоемкостей дают для интервала температур от 0 до ?°С. Средние теплоемкости в интервале температур и ?2 с использованием таблиц вычисляют по формуле
где с0_Г1, с0_Г2 — средние табличные теплоемкости газа в интервале температур (0—и (0—?2), °С.
В (1.30) числитель представляет собой количество теплоты, подводимой к газу с целью повышения его температуры от до ?2> °С.
Часто в теплотехнических расчетах криволинейную зависимость теплоемкости от температуры заменяют близкой к ней прямолинейной зависимостью (рис. 1.1). В этом случае истинную теплоемкость определяют но следующей приближенной формуле:

Рис. 1.1. Зависимость теплоемкости от температуры
Графически коэффициент а выражает теплоемкость газа при 0°С, а коэффициент Ь является тангенсом угла а наклона прямой. В таком случае среднюю теплоемкость газа в интервале температур от Ьх до ?2 находят по формуле
Расчетные приближенные формулы для определения средних теплоемкостей при постоянном давлении для различных газов в интервале температур от 0 до 1000°С приведены в специальных таблицах. Использование (1.31) и (1.32) позволяет обойтись при расчетах без справочных таблиц.
На теплоемкость реальных газов влияет не только температура, но и давление.
Для определения теплоемкости смеси газов необходимо знать ее состав и значения теплоемкостей компонентов.
При нагреве смеси на 1°С каждый компонент также нагревается на 1°С. Следовательно, если смесь задана массовыми долями, то теплоемкость смеси, кДж/К,
где Мш — масса смеси, кг; ссм — массовая теплоемкость смеси, кДж/(кг • К); М1? М2,Мп — массы компонентов, кг; сх, с2,сп — массовые теплоемкости компонентов, кДж/(кг • К).
Разделив обе части последнего уравнения на Мсм, получим
Если смесь задана объемными долями, то объемную теплоемкость 1 м 3 смеси газов при нормальных физических условиях находят по формуле
Мольную теплоемкость газовой смеси определяют но аналогичной формуле:
Видео:Основы теплотехники. Теплоёмкость газов и газовых смесей. Уравнение МайераСкачать

Уравнение Майера
Уравнение Майера связывает теплоемкости идеального газа в двух изопроцессах, тогда перейдем к самому его определению.
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Теплоемкость. Уравнение Майера
Переданное телу количество теплоты для его нагревания на 1 К получило название теплоемкости тела данной системы. Обозначение принимается буквой » С » :
Значение теплоемкости единицы молярной массы тела:
c μ = C v ( 2 ) . Выражение называется молярной теплоемкостью.
Теплоемкость не считается функцией состояния, так как является характеристикой бесконечно близких состояний системы или выражается в качестве функции бесконечно малого процесса, совершаемого в системе. В количественном выражении это означает, что из ( 1 ) , применяя первое начало термодинамики, дифференциальная форма получится:
C = δ Q d T = d U + p d V d T ( 3 ) .
Видео:Теплоемкость. Теплоемкость газа. Молярная теплоемкостьСкачать

Уравнение Майера для идеального газа
Определение термодинамической системы производится при помощи трех параметров p , V , T . Существующее между ними отношение получило название уравнения состояния. Для идеального газа используется уравнение Менделеева-Клапейрона. Данная связь запишется в виде:
p = p ( T , V ) или T = T ( p , V ) , V = V ( p , T ) .
При выборе независимых переменных в качестве V и T внутренняя энергия системы выражается в виде функции U = U ( T , V ) . Получим, что значение полного дифференциала от внутренней энергии примет вид:
d U = ∂ U ∂ T V d T + ∂ U ∂ V T d V ( 4 ) .
Произведем подстановку из ( 4 ) в ( 3 ) , тогда
c = ∂ U ∂ T V d T + ∂ U ∂ V T d V + p d V d T = ∂ U ∂ T V + p + ∂ U ∂ V T d V d T ( 5 ) .
Исходя из формулы ( 5 ) , теплоемкость находится в зависимости от процесса. Если он изохорный, то
Значение теплоемкости изохорного процесса запишется как:
C V = ∂ U ∂ T V ( 6 ) .
При изобарном теплоемкость выражается через формулу:
C p = ∂ U ∂ T V + p + ∂ U ∂ V T ∂ V ∂ T p = C V + p + ∂ U ∂ V T ∂ V ∂ T p ( 7 ) .
Перейдем к рассмотрению исследуемой системе идеального газа. Запись малого приращения энергии идеального газа:
d U = i 2 v R d T ( 8 ) .
d U d V T = 0 ( 9 ) .
Состояние идеального газа описывается при помощи уравнения Менделеева-Клапейрона:
∂ V ∂ T p = v R p ( 11 ) .
Произведем подстановку в ( 7 ) из ( 10 ) и ( 11 ) :
C p = C V + p + 0 v R p = C V + v R ( 12 ) .
Выражение ( 12 ) называют выведенным соотношением Майера.
Или для молярных теплоемкостей:
C μ p = C μ V + R ( 13 ) .
Найти удельную теплоемкость смеси 16 г кислорода и 10 г гелия в процессе с постоянным давлением.
Если Q считается количеством тепла, получаемым смесью газов в процессе, то
Q = c p m ∆ T ( 1 . 1 ) , где m является массой смеси, c p – удельной теплоемкостью смеси при неизменном давлении.
Q O 2 — это количество тепла, получаемое кислородом:
Q O 2 = c p O 2 m O 2 ∆ T ( 1 . 2 ) , m O 2 выражается массой кислорода, c p O 2 – теплоемкостью кислорода с постоянным давлением.
Для гелия аналогично:
Q H e = c p H e m H e ∆ T ( 1 . 3 ) .
Кроме этого рассмотрим:
Q = c p m ∆ T = Q O 2 + Q H e = c p O 2 m O 2 ∆ T + c p H e m H e ∆ T ( 1 . 4 ) .
Нахождение массы смеси производится по закону сохранения массы:
m = m O 2 + m H e ( 1 . 5 ) .
Произведем выражение теплоемкости c p из ( 1 . 4 ) , учитывая ( 1 . 5 ) . Тогда имеем:
c p = c p O 2 m O 2 + c p H e m H e m O 2 + m H e ( 1 . 6 ) .
Существует связь между молярной теплоемкостью и удельной:
c μ = c · μ → c = c μ μ ( 1 . 7 ) .
Если c μ V = i 2 R , то по уравнению Роберта Майера c μ p = c μ V + R :
c μ p = i + 2 2 R ( 1 . 8 ) ; i H e = 3 , i O 2 = 5 .
В данном случае удельные теплоемкости запишутся как:
c p H e = 5 2 R μ H e , c p O 2 = 7 R 2 μ O 2 ( 1 . 9 ) .
Результатом будет записанная формула удельной теплоемкости смеси:
c p = 7 R 2 μ O 2 m O 2 + 5 2 R μ H e m H e m O 2 + m H e ( 1 . 10 ) .
c p = 3 , 5 · 8 , 31 · 16 32 + 2 , 5 · 8 , 31 · 10 4 26 = 14 , 5 + 51 , 94 26 = 2 , 56 Д ж г К .
Ответ: удельная теплоемкость смеси равняется 2 , 56 Д ж г К .
При проведении опытов Джоулем было получено, что с μ p — c μ V = 1 , 986 к а л К · м о л ь . Значение газовой постоянной, измеренной в механических единицах R = 8 , 314 · 10 7 э р г К · м о л ь . Определите, как соотносятся 1 к а л , э р г , Д ж .
Основой решения данного задания принято считать уравнение Майера, формула записывается:
с μ p = c μ V + R → c μ p — c μ V = R ( 2 . 1 ) .
Отсюда получим, что:
c μ p — c μ V = 1 , 986 к а л К · м о л ь = 8 , 314 · 10 7 э р г К · м о л ь → 1 к а л = 4 , 18 · 10 7 э р г = 4 , 18 Д ж .
Ответ: 1 к а л = 4 , 18 · 10 7 э р г = 4 , 18 Д ж .
Видео:О.Я. Савченко 5.6.28* | Вывод уравнения политропыСкачать

Газовые смеси и теплоемкости
Методические указания
В инженерной практике часто приходится иметь дело с газообразными веществами, близкими по свойствам к идеальным газам и представляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые смеси.
Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в неё компонентов
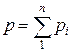
Состав газовой смеси определяется количеством каждого из газов, входящих в смесь, и может быть задан массовыми или объёмными долями. Массовая доля определяется отношением массы отдельного газа входящего в смесь, к массе всей смеси
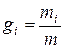
где gi – массовая доля компонента смеси;
m – масса всей смеси, кг.
Объёмной долей газа называется отношение объёма каждого компонента, входящего в смесь, к объёму всей газовой смеси при условии, что объём каждого компонента, отнесён к давлению и температуре смеси
где ri – объёмная доля компонента смеси;
Vi – приведённые объёмы компонентов газов, входящих в смесь, м 3 ;
V – общий объём газовой смеси, м 3 .
Очевидно, что 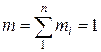

Основные формулы, применяемые при расчётах газовых смесей, приведены в таблице 1.1.1.
Таблица 1.1.1 – Формулы для расчёта газовых смесей
| Состав смеси | Перевод из одного состава в другой | Удельный объём смеси | Кажущаяся молекулярная масса смеси | Газовая постоянная смеси | Парциальное давление |
| Массовые доли | 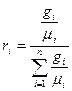 | 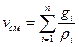 |  | 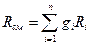 | 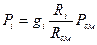 |
| Объёмные доли | 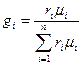 | 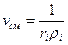 |  | 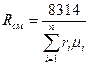 |  |
Теплоемкостью называют количество теплоты, которое необходимо сообщить телу (газу), чтобы повысить температуру какой-либо количественной единицы на 1 0 С. В зависимости от выбранной количественной единицы вещества различают удельные мольную 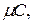

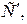
1 м 3 газа в зависимости от параметров его состояния имеет разные массы. В связи с этим объемную теплоемкость всегда относят к массе газа, заключенной в 1 м 3 его при нормальных условиях Рн = 101325 Па (760 мм.рт.ст.) и Т = 273 К (t =0 0 С). Для определения значений перечисленных выше теплоёмкостей достаточно знать величину одной какой-либо из них. Удобнее всего иметь величину мольной теплоемкости. Тогда массовая теплоемкость 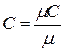



Теплоемкость газа зависит от его температуры. По этому признаку различают среднюю и истинную теплоемкость. Если q — количество теплоты, сообщаемой единице количества газа (или отнимаемого от него) при изменении температуры газа от t1 до t2 то средняя теплоемкость впределах температур 
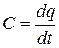
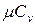
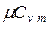
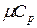

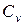
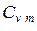


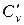
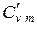
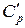
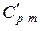
Между мольными теплоемкостями при р=const и v=const существует следующая зависимость: 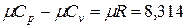
Для приближённых расчётов при невысоких температурах можно принять значения мольных теплоёмкостей указанные в таблице 1.1.2.
Отношение теплоёмкостей при р=const и v=const обозначается
Таблица 1.1.2 – Значения мольных теплоёмкостей при р=const и v=const
| Газы | Мольная теплоёмкость | 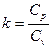 | |
 | 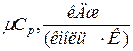 | ||
| Одноатомные | 12,56 | 20,93 | 1,67 |
| Двухатомные | 20,93 | 29,31 | 1,41 |
| Трёх и многоатомные | 29,31 | 37,68 | 1,29 |
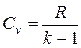
Количество теплоты, которое участвует в процессе нагревания (охлаждения) М, кг или V, м 3 газа
Теплоёмкость газов изменяется с изменением температуры, причём эта зависимость носит криволинейный характер. Нелинейную зависимость истинной теплоёмкости от температуры представляют в виде
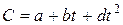
где a, b, d – величины постоянные для данного газа.
В расчётах нелинейную зависимость заменяют близкой к ней линейной зависимостью 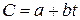
Для средней теплоёмкости в пределах 0 0 —t эта формула принимает вид
Теплоёмкость смеси идеальных газов
Если смесь газов задана массовыми долями, то её массовая теплоёмкость определяется как сумма произведений массовых долей на массовую теплоёмкость каждого компонента 
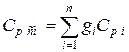
При задании смеси объёмными долями объёмная теплоёмкость смеси 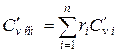

Аналогично мольная теплоёмкость смеси равна сумме произведений объёмных долей на мольные теплоёмкости составляющих смесь газов 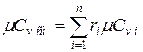
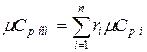
В приложениях 2-9 приведены теплоёмкости наиболее часто встречающихся в расчётах газов.
Задание №1
Газовая смесь задана в массовых gi или объемных ri долях процентным составом компонентов смеси; давление смеси Рсм, МПа, объём смеси Vсм, м 3 температура смеси tсм, 0 С (таблица 1.2.1).
1. Состав смеси (если по условию состав смеси задан в объемных долях ri, то следует определить дополнительно состав смеси в массовых долях gi и наоборот);
2. Газовые постоянные компонентов смеси Ri, кДж/(кг·К);
3. Газовую постоянную смеси Rсм, кДж/(кг·К) через объёмные и массовые доли;
4. Среднюю молярную массу смеси μсм, кмоль/кг через объемные ri и массовые gi доли;
5. Парциальные давления компонентов Рi,МПа через объемные ri и массовые gi доли;
7. Парциальные объёмы 
9. Плотности компонентов ρi, кг/м 3 при нормальных физических условиях;
10. Плотность смеси ρсм, кг/м 3 при нормальных физических условиях через объемные ri и массовые gi доли;
11. Истинную молярную μС, кДж/(кмоль·К) , объемную 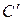
12. Среднюю молярную μС, кДж/(кмоль·К) , объемную 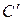
13. Количество теплоты, необходимое на нагревание (охлаждение) в интервале температур Δtсм,, 0 С при р=const и v=const количества вещества 2 кмоль, 5 м 3 и 7 кг смеси.
Таблица 1.2.1– Параметры газовой смеси
| № вар | Состав смеси | Давление смеси, Рсм, МПа | Объём смеси, Vсм, м 3 | Температура смеси, tсм,, 0 С | Интервал температур, Δtсм,, 0 С | |
| СО2 | Н2 | СО | N2 | Н2О | SO2 | O2 |
| — | — | — | 0,095 | 200-1000 | ||
| — | — | — | 0,1 | 300-100 | ||
| — | — | — | 0,09 | 100-300 | ||
| — | — | — | 0,105 | 600-200 | ||
| — | — | — | 0,105 | 1000-100 | ||
| — | — | — | 0,085 | 900-200 | ||
| — | — | — | 0,07 | 700-500 | ||
| — | — | — | — | 0,095 | 500-200 | |
| — | — | — | 0,1 | 800-300 | ||
| — | — | — | 0,105 | 600-100 | ||
| Продолжение таблицы 1.2.1 | ||||||
| № вар | Состав смеси | Давление смеси, Рсм, МПа | Объём смеси, Vсм, м 3 | Температура смеси, tсм,, 0 С | Интервал температур, Δtсм,, 0 С | |
| СО2 | Н2 | СО | N2 | Н2О | SO2 | O2 |
| — | — | — | 0,115 | 750-250 | ||
| — | — | — | 0,12 | 1000-500 | ||
| — | — | — | 0,125 | 300-1300 | ||
| — | — | — | 0,105 | 600-900 | ||
| — | — | — | 0,085 | 100-400 | ||
| — | — | — | 0,12 | 850-350 | ||
| — | — | — | 0,10 | 350-750 | ||
| — | — | — | 0,09 | 900-600 | ||
| — | — | — | 0,1 | 450-300 | ||
| — | — | — | 0,105 | 300-150 | ||
| — | — | — | 0,105 | 800-300 | ||
| — | — | — | 0,1 | 400-300 | ||
| — | — | — | 0,095 | 800-300 | ||
| — | — | — | 0,115 | 650-150 | ||
| — | — | — | 0,085 | 150-1200 | ||
| — | — | — | 0,1 | 300-800 | ||
| — | — | — | 0,1 | 1200-1000 | ||
| — | — | — | 0,09 | 400-900 | ||
| — | — | — | 0,095 | 800-600 | ||
| — | — | — | 0,1 | 600-100 | ||
| — | — | — | 0,11 | 500-1000 | ||
| — | — | — | — | 0,10 | 500-200 | |
| — | — | — | 0,085 | 800-250 | ||
| — | — | — | 0,10 | 200-700 | ||
| — | — | — | 0,095 | 400-100 |
Пример решения задания
Смесь имеет следующий объемный состав:
СО2=12%; 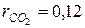 ; ; | Н 2О=8%; 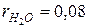 ; ; |
N2=75%; 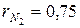 ; ; | О 2 =5%; 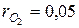 . . |
Всего 100%; 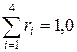
Объем смеси Vcм=3 м 3 ; давление смеси Рсм =0,1МПа; температура смеси tcм=100 0 С (Тсм=373 К). Температуру, при которой определяется истинная теплоемкость смеси t=2000 0 С (Т=2273 К) Интервал температур, для которого определяется средняя теплоемкость смеси t1=200 0 С (T1=473К); t2=1000 0 C (Т2=1273К). Провести расчет в соответствии с заданием (п. 1.2)
1. Определяем состав смеси в массовых долях

где μi – молярная масса компонента смеси, кг/кмоль (приложение 1).

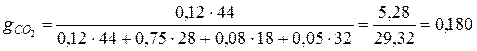
Аналогично для остальных компонентов смеси
 | 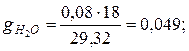 |  |
Проверка
2. Определяем газовые постоянные компонентов смеси
 | |
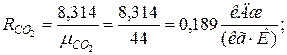 | 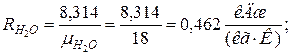 |
 | 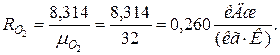 |
3. Определяем газовую постоянную смеси:
а) через объёмные 
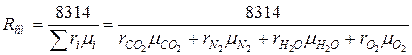
б) через массовые 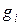
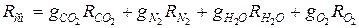
4. Находим среднюю молярную массу смеси
а) через объёмные 
б) через массовые 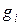
Проверка
5. Определяем парциальные давления компонентов смеси:
а) через объёмные 
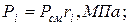 | |
 |  |
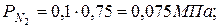 |  |
б) через массовые 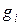
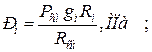 | |
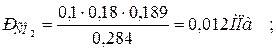 | 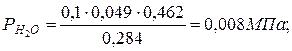 |
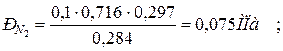 | 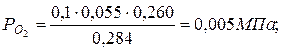 |
Проверка
6. Находим массу смеси
Определяем массу компонентов газовой смеси
 | |
 |  |
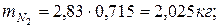 |  |
Проверка
7. Определяем парциальные объемы компонентов смеси
 ; ; | |
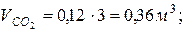 | 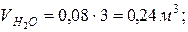 |
 | 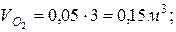 |
Проверка
Парциальные удельные объемы компонентов смеси
 , где , где 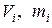 — парциальный объём и масса конкретного газа — парциальный объём и масса конкретного газа | |
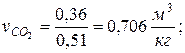 | 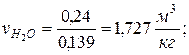 |
 | 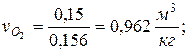 |
Находим плотности компонентов смеси
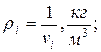 | |
 | 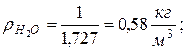 |
 | 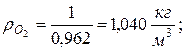 |
8. Плотности компонентов и смеси при заданных условиях Рсм и tсм
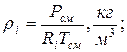 | |
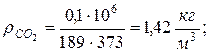 | 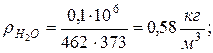 |
 | 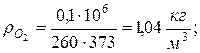 |
 | 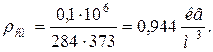 |
9. Определяем плотности компонентов смеси при нормальных физических условиях НФУ ( 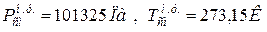
 | |
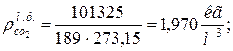 | 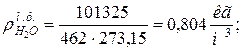 |
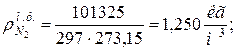 | 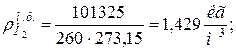 |
10. Определяем плотность смеси при НФУ:
а) через объемные ri доли
б) через массовые 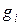
11. Находим истинную теплоемкость смеси (при tсм=2000 0 С)
а) молярная теплоёмкость смеси при р=const
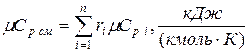
где 

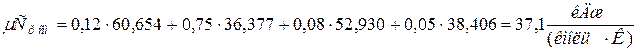
молярная теплоёмкость смеси при v=const
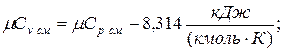 | 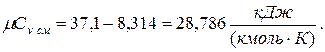 |
б) объемная теплоёмкость смеси при р=const и v=const
 | 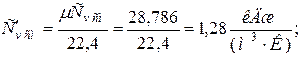 |
в) массовая теплоёмкость смеси при р=const и v=const
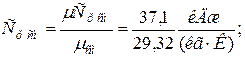 | 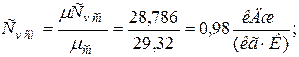 |
12. Определяем среднюю теплоемкость смеси в интервале температур
а) средняя молярная теплоёмкость смеси при р=const
где 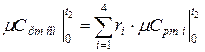
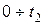

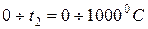
Аналогично находим среднюю молярную теплоёмкость смеси при р=const в интервале температур
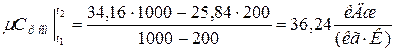
Средняя молярная теплоёмкость смеси при v=const
б) средняя объемная теплоёмкость при р=const 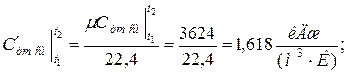 средняя объёмная теплоёмкость при v=const средняя объёмная теплоёмкость при v=const 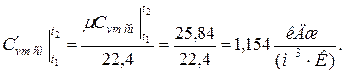 в) средняя массовая теплоёмкость при р=const в) средняя массовая теплоёмкость при р=const 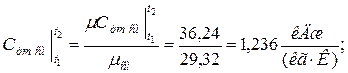 массовая теплоёмкость при v=const массовая теплоёмкость при v=const 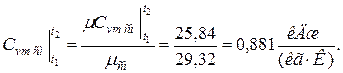 11. Определяем количество теплоты, необходимое на нагревание (охлаждение) смеси при р=const: а) 2 кмоль смеси 11. Определяем количество теплоты, необходимое на нагревание (охлаждение) смеси при р=const: а) 2 кмоль смеси 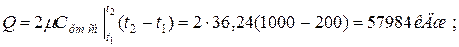 б) 5 м 3 смеси б) 5 м 3 смеси  в) 7 кг смеси в) 7 кг смеси 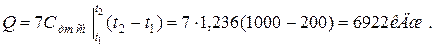 Количество теплоты, необходимое на нагревание смеси при v=const: а) 2 кмоль смеси Количество теплоты, необходимое на нагревание смеси при v=const: а) 2 кмоль смеси 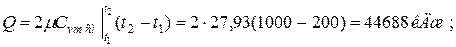 б) 5 м 3 смеси б) 5 м 3 смеси 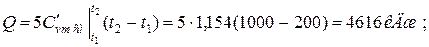 в) 7 кг смеси в) 7 кг смеси 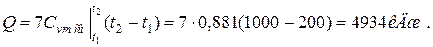 |
Термодинамические циклы
Методические указания
Круговым процессом или циклом называется совокупность термодинамических процессов, в результате осуществления которых рабочее тело возвращается в исходное состояние. Работа кругового процесса изображается в диаграмме P-v площадью, заключённой внутри замкнутого контура цикла, причём работа положительна, если цикл совершается по часовой стрелке (прямой цикл), и отрицательна, если он совершается против часовой стрелки (обратный цикл).Степень совершенства процесса превращения теплоты в работу в круговых процессах характеризуется термическим КПД
Цикл идеальной тепловой машины представляет собой цикл Карно. При его осуществлении предполагается использование горячего источника с постоянной температурой, т. е. фактически с бесконечной теплоемкостью. Цикл состоит из двух адиабат и двух изотерм. Количество подведённой теплоты
Количество отведённой теплоты
Термический КПД цикла
где Т1 и Т2 – температуры верхнего и нижнего источников теплоты.
Цикл с подводом теплоты при постоянном объёме состоит из двух адиабат и двух изохор.
Характеристиками цикла являются
— степень сжатия 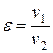
— степень повышения давления 
Количество подведенной теплоты
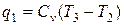
Количество отведённой теплоты
Количество тепла за цикл
Изменение внутренней энергии, энтальпии и энтропии за цикл
Термический КПД цикла
Цикл с подводом теплоты при постоянном давлении состоит из двух адиабат, одной изобары и одной изохоры.
Характеристиками цикла являются
— степень сжатия 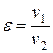
— степень предварительного расширения 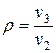
Количество подведенной теплоты

Количество отведённой теплоты
Количество тепла за цикл
Изменение внутренней энергии, энтальпии и энтропии за цикл
Термический КПД цикла
Цикл с комбинированным подводом теплоты состоит из двух адиабат, двух изохор и одной изобары.
Характеристиками цикла являются
— степень сжатия 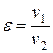
— степень повышения давления 
— степень предварительного расширения 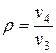
Количество подведенной теплоты
Количество отведённой теплоты
Количество тепла за цикл
Изменение внутренней энергии, энтальпии и энтропии за цикл
Термический КПД цикла
Во всех случаях с=const.
Цикл газовой турбины с подводом теплоты при постоянном давлении состоит из двух адиабат и двух изобар.
Характеристиками цикла являются
— степень повышения давления в компрессоре 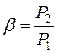
— степень сжатия 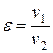
— степень расширения 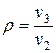
Термический КПД цикла
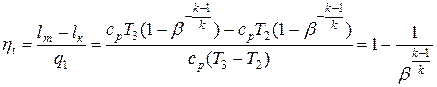
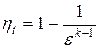
Цикл газовой турбины с подводом теплоты при постоянном объёме состоит из двух адиабат, одной изохоры и одной изобары
Характеристиками цикла являются
— степень сжатия 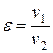
— степень добавочного повышения давления 
— степень расширения 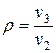
Термический КПД цикла
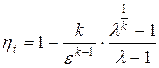
Так как уходящие из газовой турбины продукты сгорания имеют достаточно высокую температуру, то для повышения экономичности газотурбинного агрегата вводят регенерацию, т.е. предварительный подогрев сжатого в компрессоре воздуха за счёт теплоты, уходящих газов. Термический КПД цикла турбины с подводом теплоты при р=constс полной предельной регенерацией и адиабатным сжатием
Термический КПД цикла турбины с подводом теплоты при v=constc предельной регенерацией и адиабатным сжатием
Коэффициент полезного действия идеального цикла ГТУ
При этом теплоемкость ср принята для простоты постоянной. Одной из основных характеристик цикла является степень повышения давления в компрессоре 
Задание №2
Для заданного варианта цикла теплового двигателя (2.2.1 – 2.2.5) выполнить следующие теоретические, расчетные и графические работы:
1. Дать краткое, описание цикла в целом и характеристику каждого его процесса;
2. Определить параметры р, v, T во всех характерных точках цикла;
3. Провести полный термодинамический расчет каждого процесса;
4. Вычислить термодинамические характеристики цикла;
5. Вычислить термический КПД идеализированного цикла, у которого теплообменом в процессах сжатия и расширения пренебрегают;
6. Вычислить термический КПД цикла Карно осуществляемого в том же интервале температур и энтропии;
7. Изобразить цикл в р—v и Т—S координатах;
8. Определить коэффициент заполнения цикла;
9. Определить среднеинтегральную температуру процесса отвода тепла;
10. На основе расчета сделать заключение и результаты свести в таблицу.
Во всех случаях в качестве рабочего тела принимать воздух. Расчет произвести на 1 кг рабочего тела. Учитывать зависимость теплоемкости от температуры.
🔥 Видео
Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Объемные отношения газов при химических реакциях. 8 класс.Скачать

Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Количество теплоты, удельная теплоемкость вещества. Практическая часть - решение задачи. 8 класс.Скачать

30. Политропические процессыСкачать

Урок 109 (осн). Задачи на вычисление количества теплотыСкачать

Рассмотрение темы: "Теплоёмкость газов"Скачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Физика. МКТ: Смеси газов. Закон Дальтона. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Урок 108 (осн). Теплоемкость тела. Удельная теплоемкость веществаСкачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Молярная теплоёмкость при постоянном объёме и постоянном давлении.Скачать