| Уравнения плоской и сферической волн |   |
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид: Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при Видео:Колебания и волны. Лекция 10. Уравнения сферической и плоской волныСкачать  Уравнение для плоской затухающей волныотстоящие друг от друга на расстоянии λ, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции . в случае плоской волны, предполагая, что колебания носят гармонический характер. Пусть колебание точек, лежащих в плоскости x = 0, имеет вид (при начальной фазе ф = 0) Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время τ = х/v. Следовательно, колебания частиц в плоскости x будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т. е. — это уравнение плоской волны (рис. 2.4.3). Таким образом, . есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания A = const. Это будет, если энергия волны не поглощается средой. Такой же вид уравнение (2.4.5) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так: Выражения (2.4.5) и (2.4.6) есть уравнения бегущей волны. Уравнение волны можно записать и в другом виде. Введем волновое число k = 2π/λ, или в векторной форме где k — волновой вектор; n — нормаль к волновой поверхности. Так как λ = vT , то k = 2π/vT = 2πν/v = ω/v. Отсюда v = ω/k. Тогда уравнение плоской волны запишется так: Видео:10й класс; Физика; "Уравнение плоской волны"Скачать  Уравнение плоской и сферической волнПри описании волнового процесса требуется найти амплитуды и фазы колебательного движения в различных точках среды и изменение этих величин с течением времени. Эта задача может быть решена в том случае, если известно, по какому закону колеблется и как взаимодействует со средой тело, вызвавшее волновой процесс. Однако во многих случаях не существенно, каким телом возбуждена данная волна, а решается более простая задача. Задано состояние колебательного движения в некоторых точках среды в определенный момент времени и требуется определить состояние колебательного движения в других точках среды. Для примера рассмотрим решение такой задачи в простом, но вместе с тем важным случае распространения в среде плоской или сферической гармонической волны. Обозначим колеблющуюся величину через u. Этой величиной могут быть: смещение частиц среды относительно их положения равновесия, отклонения давления в данном месте среды от равновесного значения и т.д. Тогда задача будет состоять в отыскании так называемого уравнения волны – выражения, которое задает колеблющуюся величину u как функцию координат точек среды x, y, z и времени t: Пусть для простоты u – это смещение точек в упругой среде, когда в ней распространяется плоская волна, а колебания точек имеют гармонический характер. Кроме того, направим оси координат так, чтобы ось 0х совпала с направлением распространения волны. Тогда волновые поверхности (семейство плоскостей) будут перпендикулярными к оси 0х (рис. 7), и поскольку все точки волновой поверхности колеблются одинаково, смещение u будет зависеть только от х и t: u = u(x, t). Для гармонических колебаний точек, лежащих в плоскости х = 0 (рис. 9), справедливо уравнение:
Найдем вид колебаний точек плоскости, соответствующей произвольному значению х. Для того чтобы пройти путь от плоскости х = 0 до этой плоскости, волне требуется время τ = х/с (с – скорость распространения волны). Следовательно, колебания частиц, лежащих в плоскости х, будут иметь вид: Итак, уравнение плоской волны (и продольной, и поперечной), распространяющейся в направлении оси 0х, выглядит следующим образом: Величина А представляет собой амплитуду волны. Начальная фаза волны α определяется выбором начал отсчета х и t. Зафиксируем какое-либо значение фазы, стоящей в квадратных скобках уравнения (2.3), положив Продифференцируем это равенство по времени с учетом того, что циклическая частота ω и начальная фаза α являются постоянными: Таким образом, скорость распространения волны с в уравнении (2.3) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью. В соответствии с (2.5) dx/dt > 0. Следовательно, уравнение (2.3) описывает волну, распространяющуюся в направлении возрастания х, так называемую бегущую прогрессивную волну. Волна, распространяющаяся в противоположном направлении, описывается уравнением и называется бегущей регрессивной волной. Действительно, приравняв константе фазу волны (2.6) и продифференцировав получившееся равенство, придем к соотношению: из которого следует, что волна (2.6) распространяется в сторону убывания х. которая называется волновым числом и равна количеству длин волн, укладывающихся на интервале 2π метров. С помощью формул λ = с/ν и ω = 2πν волновое число можно представить в виде Раскрыв скобки в формулах (2.3) и (2.6) и приняв во внимание (2.8), придем к следующему уравнению плоских волн, распространяющихся вдоль (знак «-») и против (знак «+») оси 0х: При выводе формул (2.3) и (2.6) предполагалось, что амплитуда колебаний не зависит от х. Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. Опыт показывает, что в поглощающей среде интенсивность волны по мере удаления от источника колебаний постепенно уменьшается – наблюдается затухание волны по экспоненциальному закону: Соответственно, уравнение плоской затухающей волны имеет вид: где A0 – амплитуда в точках плоскости х = 0, а γ – коэффициент затухания. Теперь найдем уравнение сферической волны. Всякий реальный источник волн обладает некоторой протяженностью. Однако если ограничиться рассмотрением волны на расстояниях от источника, много больших его размеров, то источник можно считать точечным. В изотропной и однородной среде волна, порождаемая точечным источником, будет сферической. Допустим, что фаза колебаний источника ωt+α. Тогда точки, лежащие на волновой поверхности радиуса r, будут колебаться с фазой Амплитуда колебаний в этом случае, даже если энергия волны не поглощается средой, постоянной не останется – она убывает в зависимости от расстояния от источника по закону 1/r. Следовательно, уравнение сферической волны имеет вид: где А – постоянная величина, численно равная амплитуде колебаний на расстоянии от источника, равном единице. Для поглощающей среды в (2.11) нужно добавить множитель e — γr . Напомним, что в силу сделанных предположений уравнение (2.11) справедливо только для r, значительно превышающих размеры источника колебаний. При стремлении r к нулю амплитуда обращается в бесконечность. Этот абсурдный результат объясняется неприменимостью уравнения (2.11) для малых r. 💥 ВидеоПолучение уравнения плоской бегущей волны.Скачать  Билет №34 "Электромагнитные волны"Скачать  4.3 Плоские электромагнитные волны в идеальных диэлектрических средахСкачать  Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать  Уравнения и графики механических гармонических колебаний. 11 класс.Скачать  Механические модели волн. 1.Скачать  Урок 370. Механические волны. Математическое описание бегущей волныСкачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать  Раскрытие тайн электромагнитной волныСкачать  Билеты № 35, 39 "Плоская волна, ее отражение. Давление излучения"Скачать  🌊 Продольные и поперечные волны ⚛ ФизикаСкачать 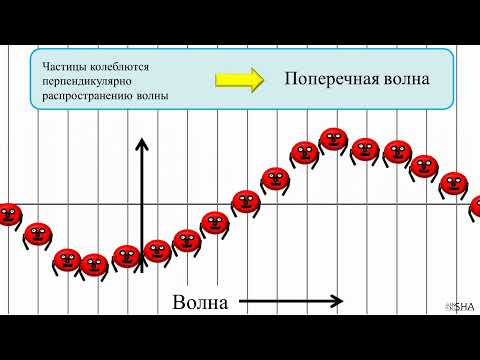 Урок №45. Электромагнитные волны. Радиоволны.Скачать  Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать  Урок 384. Излучение электромагнитных волн.Скачать  4.4 Плоские электромагнитные волны в проводящих средахСкачать  Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать  Упругие механические волны. 1 часть. 11 класс.Скачать  |

 .
. . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)

 .
. ,
, . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или  .
. .
. , или в векторной форме:
, или в векторной форме: ,
, – волновой вектор,
– волновой вектор,  – нормаль к волновой поверхности.
– нормаль к волновой поверхности. , то
, то  . Отсюда
. Отсюда  . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: .
. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: , или
, или  ,
, , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний  , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.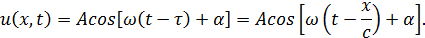
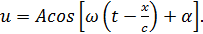 (2.3)
(2.3) (2.4)
(2.4)
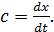 (2.5)
(2.5) (2.6)
(2.6)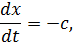
 (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9)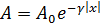 .
. (2.10)
(2.10)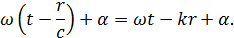
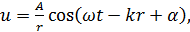 (2.11)
(2.11)