Под балансными (равновесными) мостовыми схемами понимают такие схемы, которые работают в равновесном режиме. При изменении величины сопротивления в одном из плеч регулировкой сопротивлений в других плечах моста добиваются отсутствия тока через гальванометр, а отсчет производят на регулируемом элементе.
Равновесные мосты выполняются как с ручным, так и с автоматическим уравновешиванием. Те и другие обладают рядом свойств, присущих только балансным мостам.
1. Равновесные мосты обладают малой погрешностью (до 0,01% и даже 0,001%).
Это объясняется тем, что индикатор работает в нулевом режиме, и его погрешность не входит в погрешность измерения. Остальные же элементы моста могут быть выполнены с достаточной точностью.
2. Равновесие балансных мостов не будет нарушено при колебаниях величины и частоты питающего напряжения. Влияние изменения частоты источника питания может быть лишь в том случае, если при этом изменяются составляющие сопротивлений измерительной цепи и фазовые соотношения в ней, т. е. при неоднородности плеч моста.
3. Применение равновесных мостов дает возможность увеличить чувствительность схемы за счет применения ламповых усилителей, которые в этих цепях практически не вносят погрешности, обусловленной непостоянством коэффициента усиления.
4. При использовании равновесных мостов при необходимости может быть получена достаточно линейная шкала, применением специальных устройств, например, изготовлением плеча уравновешивания в виде нелинейного потенциометра.
5. Равновесные мосты, благодаря наличию в них уравновешивающих устройств, являются сложными приборами.
3. Равновесные мосты имеют малое быстродействие за счет инерционности преобразователя и уравновешивающего устройства.
При некоторых технических измерениях не требуется той высокой точности, которую могут обеспечить только равновесные мосты. В то же время их сложность, необходимость в балансировке и относительно малое быстродействие измерений являются достаточно существенными недостатками последних.
Большинство современных измерений неэлектрических величин электрическими методами не требует допустимой погрешности, меньшей 0,5-1,0%, так как часто погрешности самих преобразователей довольно велики. Но зато требуются более простые устройства с достаточно быстрым отсчетом измеряемой величины непосредственно по шкале измерительного устройства.
Этим требованиям удовлетворяют неравновесные мосты. Принцип действия таких мостов заключается в том, что при выходе моста из состояния равновесия из-за изменения сопротивления в одном из плеч в указательной диагонали появляется ток, связанный функционально с приращением сопротивления изменившегося плеча и измеряемый соответствующим прибором.
Точность измерения с помощью неравновесных мостов в основном определяется точностью измерительного прибора, по которому непосредственно производится отсчет, и точностью преобразователя, так как плечи моста выполняются, как правило, с очень малой погрешностью. Кроме того, точность неравновесных мостов зависит от изменения внешних факторов (изменения температуры окружающей среды, изменения величины и частоты питающего напряжения и т. д.).
Однако, путем определенного включения преобразователей, применения логометрического измерителя, стабилизации напряжения и частоты источника питания и других мер, о чем будет сказано ниже, удается избавиться частично или полностью от этих погрешностей. Однако, выбирая меры для уменьшения дополнительных погрешностей, следует подходить к этому критически. Например, если в качестве измерителя используется прибор класса 1,5 (т.е. с основной приведенной погрешностью, равной ± 1,5%), то нет смысла стабилизировать напряжение источника питания с точностью до десятых долей процента и нет смысла добиваться стабильности коэффициентов усиления усилителей с точностью более чем 1-1,5%, а значит применять высокостабильные и дорогостоящие элементы схемы и т. д..
Кроме невысокой точности, недостатком неравновесных мостов является трудность получения линейной шкалы: ток указателя мостовой схемы нелинейно связан с изменением сопротивлений плеч моста и компенсировать эту нелинейность нелинейностью датчика не представляется возможным.
Видео:Лекция 176. Мостовые измерительные схемыСкачать
Мостовые схемы
Мостовые схемы широко используются в приборах для измерения параметров электрических цепей (R, С, М, L, f ) и разнообразных неэлектрических величин, преобразуемых в параметры R, С, М, L, f.
Условием равновесия моста, т. е. равенства нулю тока гальвано метра IГ, является равенство
Откуда измеряемое сопротивление
Мостовые схемы работают как в неравновесном, так и в равновесном режимах. В первом случае мост уравновешивается при начальном значении сопротивления R1 = Rх0 при изменении Rx, т. е. при Rx Rx0 мост выходит из равновесия и в измерителе появляется ток IГ. Шкала измерителя градуируется непосредственно в единицах Rx. При этом ток IГ зависит не только от соотношения сопротивлений плеч моста, но и от значений питающего напряжения U или тока I.
Поэтому при колебаниях питающего напряжения U возникает дополнительная погрешность.
При работе в равновесном режиме мост уравновешивается при любом значении Rx путем изменения сопротивления любого из остальных плеч. В настоящее время широко применяются автоматические мосты, в которых процесс уравновешивания осуществляется устройством, следящим за возникновением неравновесия.
Чаще всего мостовые цепи на переменном токе применяются в равновесном режиме.
На рис. 6.3, б представлена мостовая цепь переменного тока. На схеме а и b — точки моста; с и d — диагональ моста; Г — измеритель. Предположим, что все четыре плеча моста содержат как активные, так и реактивные сопротивления. Условие равновесия моста в этом случае будет выражаться равенством
Видео:лекция 10. Расчет Мостовой СхемыСкачать
Уравнение для неравновесной мостовой схемы
Никакую книгу по электрическим измерениям нельзя было бы назвать полной без раздела о мостовых схемах. Эти гениальные схемы используют индикатор баланса для сравнения двух напряжений, точно так же как и лабораторные весы сравнивают две массы и указывают на то, что они равны. В отличие от «потенциометрических» схем, используемых для простого измерения неизвестного напряжения, мостовые схемы могут использоваться для измерения всех видов электрических величин, в том числе и сопротивлений.
Стандартная мостовая схема, часто называемая мостом Уитстона (Wheatstone bridge), изображена на рисунке 1.
Когда напряжение между точкой 1 и минусом батареи равно напряжению между точкой 2 и отрицательным выводом батареи, то индикатор баланса будет показывать ноль, и про такой мост говорят что он «сбалансирован». Состояние баланса моста полностью зависит от отношений Ra/Rb и R1/R2, и оно не зависит от напряжения питания. Для измерения сопротивлений с помощью моста Уитстона на место резисторов Ra или Rb устанавливается неизвестное сопротивление, в то время как остальные три резистора являются прецизионными и их номинал известен. Каждый из этих трёх резисторов может быть заменён сопротивлением другой величины или их номиналы могут быть скорректированы, что бы мост сбалансировался, и когда это произойдёт то величина сопротивления неизвестного резистора может быть определена из соотношения величин известных сопротивлений.
Для этого необходимо, что бы измерительная система имела набор переменных резисторов с точно известными значениями, которые могут служить эталонными стандартами. Например, если мост настроен на измерение сопротивления Rx (рисунок 2), то мы должны знать точное значение остальных трёх сопротивлений при сбалансированном мосте, что бы определить величину сопротивления Rx:
Каждое из четырёх сопротивлений в мостовой схеме называют плечом. Резистор, последовательно соединённый с неизвестным сопротивлением, Rx обычно называют реостатом моста (это будет сопротивление Ra на рисунке 2), а другие два сопротивления называют плечами отношений моста.
Точные и стабильные образцовые сопротивления к счастью, не сложно изготовить. В действительности они были одними из первых электрических «Стандартных» устройств, изготовленных в научных целях. На рисунке 3 приведена фотография старинного блока стандартных сопротивлений:
Рис. 3. Магазин образцовых сопротивлений
Стандарт сопротивлений, изображённый на рисунке 3, является переменным с дискретным шагом изменения сопротивления: величина сопротивления между клеммами может изменяться в зависимости от количества и положения медных вставок, вставленных в разъёмы.
Мосты Уитстона считаются превосходным средством измерения сопротивления среди схем различных омметров. Но в отличие от всех этих схем, являющихся нелинейными (и имеющих нелинейные шкалы), и связанные с этим погрешности измерений, мостовая схема является линейной (математика описания её работы основана на простых отношениях и пропорциях) и довольно точной.
Имея стандартные сопротивления достаточной точности и нуль-детектор с необходимой чувствительностью, достижимая точность измерения сопротивления может быть не хуже +-0,05% при использовании моста Уитстона. Это метод измерения сопротивления предпочитают использовать в калибровочных лабораториях из-за его высокой точности.
Существует много вариаций основной схемы моста Уитстона. Большинство мостов постоянного тока используются для измерения сопротивления, в то время как мосты переменного тока могут быть использованы для измерения различных электрических величин, таких как индуктивность, ёмкость и частота.
Интересным вариантом моста Уитстона является двойной мост Кельвина, используемый для измерения очень малых сопротивлений (обычно менее 1/10 Ома), его схема изображена на рисунке 4:
Рис. 4. Двойной мост Кельвина.
Ra и Rx являются низкоомными сопротивлениями.
Низкоомные резисторы на рисунке изображены толстой линией, так же как и проводники, соединяющие их с источником напряжения, обеспечивающим сильный ток. Принцип работы этого измерительного моста причудливой конфигурации, пожалуй, лучше всего понять, если начать объяснение принципа его работы со стандартного моста Уитстона, настроенного для измерения низкого сопротивления, этот мост развивался шаг за шагом до его нынешнего состояния в попытке преодолеть некоторые проблемы, возникшие в мосте Уитстона стандартной конфигурации.
Если бы мы использовали стандартный мост Уитстона для измерения небольших сопротивлений, то его схема бы выглядела примерно так (рисунок 5):
Когда нуль-детектор указывает нулевое напряжение, мы знаем, что мост сбалансирован и что соотношение Ra/Rx и RM/RN математически равны друг другу. Зная значения Ra, RM, and RN поэтому мы имеем все необходимые данные, чтобы найти величину Rx. Почти.
Имеется проблема в том, что соединения и соединительные провода между Ra и Rx обладают неким сопротивлением, и эти паразитные сопротивления могут быть существенными по сравнению с низким сопротивлением Ra и Rx. Эти паразитные сопротивления понизят реальное напряжение, учитывая большой ток, протекающий через них, и таким образом будут влиять на показания детектора нуля и на баланс моста (Рисунок 6):
Рис. 6.
Паразитное напряжение Eпров. ухудшает точность измерения Rx.
Так как мы не хотим измерять сопротивление этих паразитных проводников и сопротивление соединений, а нас интересует только измерение сопротивления Rx, то надо найти такой способ включения нуль-детектора, что бы на его показания не влияли падения напряжений, протекающего через эти сопротивления. Если мы присоединим нуль-детектор и плечи отношений RM/RN напрямую к выводам Ra и Rx, то это приведёт нас к такой реализации измерительного моста (Рисунок 7):
Рис. 7.
Теперь только два паразитных падения напряжения Eпров. являются частями цепи нуль-детектора.
Теперь два крайних падения напряжения Eпров. не оказывают воздействия на нуль-детектор и не влияют на точность измерений сопротивления Rx. Но два оставшихся падения напряжений Eпров. являются проблемой, так как проводник, соединяющий нижний по схеме вывод Ra и верхний по схеме вывод Rx теперь шунтирует оба падения напряжения и по нему будет течь существенный ток, который создаст на этом проводнике своё падение напряжения.
Зная, что левая часть нуль-детектора должна быть подключена к двум крайним выводам сопротивлений Ra и Rx, что бы не вносить ошибки, связанные с паразитными падениями напряжения Eпров. в цепи нуль-детектора, и что любой прямой провод, соединяющий выводы этих сопротивлений Ra и Rx будет сам нести значительный ток и создавать ещё большее паразитное падение напряжения, то единственным способом преодолеть эту проблему является создание соединения, имеющее существенное сопротивление, между нижнем по схеме выводом Ra и верхнем по схеме выводом Rx (Рисунок 8):
Справится с паразитными падениями напряжений между выводами сопротивлений Ra Rx можно путём изменения сопротивления двух новых резисторов таким образом, что бы отношение их величин было бы таким же, как и отношение величин сопротивлений в плече отношений, находящихся по схеме с правой стороны от нуль-детектора. Вот почему эти резисторы были помечены Rm и Rn в оригинальной схеме двойного моста Кельвина: для обозначения их соразмерности с сопротивлениями RM и RN (Рисунок 9):
Рис. 9. Двойной мост Кельвина
Ra и Rx являются низкоомными сопротивлениями.
При отношении Rm/Rn равном отношению RM/RN, резистор в плече реостата Ra регулируется до тех пор, пока нуль-индикатор не покажет, что мост сбалансирован, и тогда можно будет сказать, что отношение Ra/Rx равно отношению RM/RN, или просто найти Rx из следующего уравнения:
Полное уравнение баланса двойного моста Кельвина выглядит следующим образом (Rпров. — это сопротивление толстых соединительных проводов между низкоомным образцовым сопротивлением Ra и испытуемым сопротивлением Rx):
До тех пор пока соотношение между RM и RN равно отношению между Rm и Rn, уравнение баланса будет не сложнее чем у обычного моста Уитстона, при Rx/Ra равном RN/RM, так как последнее выражение в уравнении будет равно нулю, так что будет отсутствовать влияние всех сопротивлений, кроме Rx, Ra, RM, и RN.
Во многих двойных мостовых схемах Кельвина RM=Rm и RN=Rn. Однако чем меньше значения сопротивлений Rm и Rn, тем более чувствительным должен быть нуль-детектор, потому что там будет меньше последовательное сопротивление. Увеличение чувствительности детектора является полезным, так как оно позволит обнаруживать слабые дисбалансы, и таким образом мост можно будет сбалансировать с большой точностью. Таким образом некоторые высокоточные двойные мосты Кельвина используют сопротивления Rm и Rn со значениями в 100 раз меньше, чем значения сопротивлений RM и RN в другом плече. К сожалению, однако, чем ниже значения сопротивлений Rm и Rn, тем больший ток по ним будет течь, что увеличит влияние любого сопротивления в точке подключения Rm и Rn к Ra и Rx. Как вы можете видеть, высокая точность инструмента требует, чтобы учитывались все ошибки различных факторов, и часто лучшее, что может быть достигнуто является компромиссом минимизации двух или более различных видов ошибок.
- ИТОГ:
- Мостовые схемы используют чувствительный индикатор нуля для сравнения двух напряжений на их равенство.
- Мост Уитстона (Wheatstone bridge) может быть использован для измерения сопротивлений путём сравнения сопротивления неизвестного номинала и образцового сопротивления с известной величиной, так же как с помощью лабораторных весов измеряют неизвестный вес путём сравнения его со стандартными грузами.
- Двойной мост Кельвина является вариантом моста Уитстона для измерения очень малых сопротивлений. Его усложнение по сравнению с базовой схемой моста Уитстона является необходимым для избежания ошибок, вносимых паразитными сопротивлениями на пути тока между низкоомным образцовым сопротивлением и сопротивлением, величина которого измеряется.
🔥 Видео
Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать
Мост Уитстона и метод узловых потенциалов | Олимпиадная физика, электричество | 8, 9, 10, 11 классСкачать
ЛР-11-2-03 Измерение сопротивления проводника мостовым методомСкачать
Как составить уравнения по законам Кирхгофа?Скачать
Мост Уитстона или измерительный мост.Как это работает и что измеряетСкачать
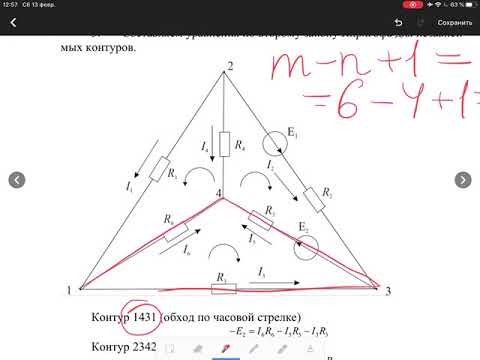
Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать
Как упрощать схемы цепей, уменьшать количество контуров. ПРИНЦИП ЭКВИВАЛЕНТНОГО ИСТОЧНИКАСкачать
Расчет статически неопределимой стержневой системы. Уравнение совместимости деформацийСкачать
Как читать принципиальные схемы? ВЫПУСК 5.Скачать
Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать
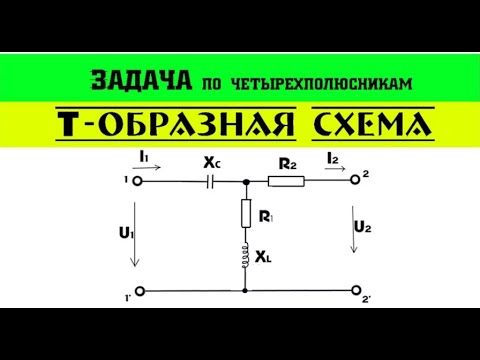
Задачи по четырехполюсникам. Т-образная схемаСкачать
Метод узловых потенциалов. Задача 2Скачать
Статически неопределимая системаСкачать
Задачи по четырехполюсникам. П - образная схемаСкачать
Термосопротивление PT100. Измерительный мост Уитстона. Диф. усилитель на ОУ. Уголок инженера#00.Скачать
Практика ОСЭ 2ф выпрямитель 1ф тока, выпрямиетль 1ф тока по мостовой схеме и 6ф выпрямитель 3ф токаСкачать
Основы параметрической формы метода наименьших квадратов (МНК) на примере уравнивания опорных сетей.Скачать
2 Лабораторная работа Тангенс мостовой методСкачать
