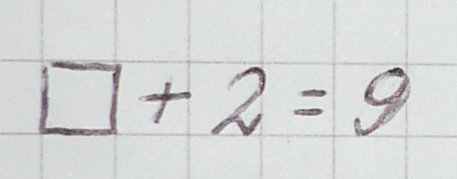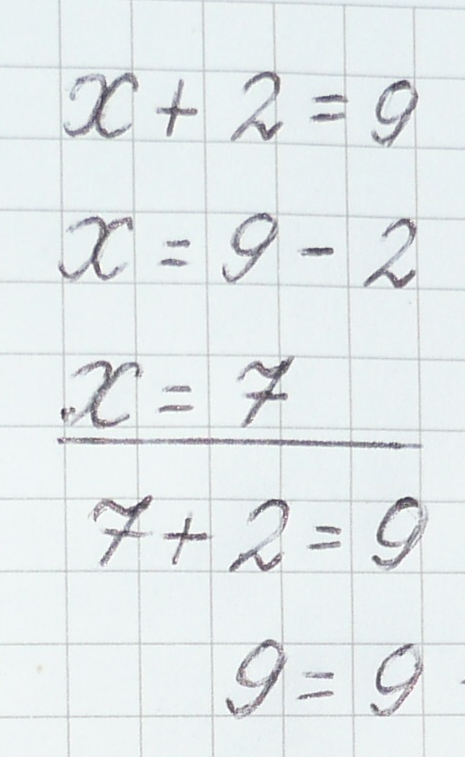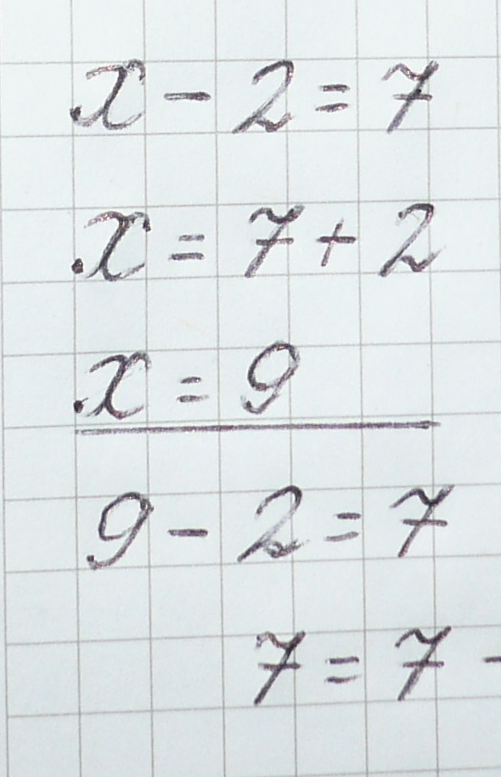Уравнение для 1 класса по математике как объяснить ребенку (5 видео)

Урок математики в 1 классе по теме: «Уравнения»

Цели. Ввести понятие уравнения, научить решать уравнения с неизвестными компонентами-слагаемыми на основе взаимосвязи между частью и целым; обрабатывать навыки быстрого и стабильного счета в пределах 9; развивать логическое мышление, внимание, память, аналитические способности.

Оборудование. Учебник “Математика. 1 класс” (сост. Л.Г. Петерсон). Издательство “С-инфо”.

I. Организационный момент

Учитель: Прочитайте, что написано?

На доске: “Если не лениться…”

У. Как бы вы продолжили? (Ответы детей). Вот как продолжила я: “Можно многого добиться”. Вы готовы не лениться?

II. Актуализация знаний и мотивация.

Проверка устного счета. Учитель диктует числовые выражения:

Дети устно считают, ответ говорят вслух. Учитель на доске записывает ответы.

У. Составьте с помощью чисел 2, 7, 5 четыре равенства. Обозначьте в них целое и части.

Проверка: один ученик на доске записывает суммы (2 + 5 = 7, 5 + 2 =7), другой – разности (7 –5 =2, 7 – 2 =5).

У. Назовите, где целое и части. Почему?

Д. 2 и 5 – это части, т.к. складывать мы можем только части. 7 – это целое, т.к. вычитать мы можем только из целого.

У. Что записано на доске?

Д. Равенства с неизвестным числом.

У. Каким образом будем считать?

Д. Методом подбора.

У. Найдите ошибки. Почему?

III. Постановка проблемы.

У. Рассмотрите вот эту запись. Что это на ваш взгляд?

На доске: Х + 2 = 5

Д. Равенство, в котором есть неизвестный компонент.

У. Такие равенства в математике называются уравнениями. (Учитель на доске вывешивает табличку с надписью “Уравнение”).

Неизвестное число в уравнениях можно обозначить по-разному, но чаще всего используют латинские буквы, например Х.

Давайте решим наше уравнение. Чему равен Х?

Д. Х равен 3.

У. Значение Х называют корнем уравнения.

У. Почему Х равен 3? Как нашли?

Д. 5 – это 2 и 3. Подобрали число.

У. Итак, мы решили уравнение с помощью подбора корней.

У. Чем это уравнение отличается от предыдущего? Сравните их.

Д. В этом уравнении даны геометрические фигуры.

У. Решим уравнение. Чему равен Х?

Д.

У. Как нашли корень уравнения?

Д. Способом подбора.

У. У вас на карточках дано уравнение. Решите его самостоятельно. Каким способом вы будете решать?

Д. Способом подбора.

У. Легко ли найти Х – корень уравнения способом подбора?

Д. Трудно.

У. Удобно подбирать геометрическую фигуру?

Д. Нет.

IV. Поиск решения.

У. Что же нам нужно сделать сегодня на уроке?

Д. Найти новый способ решения уравнения.

У. Есть такой “секрет”, который как “волшебный ключик”, поможет решить любое уравнение. Подумайте, какое действие с “мешками” нужно сделать, чтобы найти Х?

Д. Вычитание.

У. Почему?

Д. Потому, что Х – это часть.

У. А как найти часть?

Д. Из целого вычесть другую часть.

У. Зачеркните в сумме известную часть. Какие фигурки остались? Удобно так считать? Какое правило нам помогло?

Д. Чтобы найти часть, надо из целого вычесть другую часть.

У. Давайте проверим по учебнику.

с. 20 (Дети читают по учебнику правило и убеждаются в правильности своего вывода.)

Чтобы найти часть, надо из целого вычесть другую часть

V. Закрепление изученного материала с проговариванием.

У. Прочитайте уравнение. Что неизвестно?

Д. Из целого вычесть другую часть.

Уравнения можно составлять не только с геометрическими фигурами, но и с буквами.

Прочитайте уравнение.
Что неизвестно?
Как найти?
Чему равен Х?

Дети отвечают на вопросы.

VI. Самостоятельная работа по выбору.

с. 20, № 3, 4. Проверка в парах.

VII. Включение нового способа действия в систему знаний.

У. Давайте рассмотрим рисунок. Что видите?

Д. Весы в равновесии.

У. Что обозначено за Х?

Д. Масса мешка с крупой.

У. Давайте составим уравнение.

Д. Х + 2 = 4

У. Объясните по образцу как решали уравнение. (Составление алгоритма на доске).

Д.

1. Выделить части и целое.
2. Определить, что неизвестно.
3. Применить правило (как найти).
4. Найти корень уравнения.

№5 (б) – с комментированием (рассмотреть рисунок, составить уравнение, решить по алгоритму);

№5 (в) – самостоятельно с проверкой на доске:

У. Встаньте те ребята, у кого решено уравнение так, как у меня на доске.

VIII. Итог урока. Рефлексия деятельности.

У. Мы начали урок со слов: “Если не лениться, можно многого добиться”.

Кто сегодня не ленился? А чего же вы добились? Что узнали нового? Какое “открытие” сделали?

А вы хотите составить свои уравнения? У вас на столах лежат листочки. Попробуйте сейчас придумать свои уравнения. Они могут быть любые: числовые, буквенные, с использованием геометрических фигур. Пофантазируйте, как можно изобразить неизвестный компонент.

Видео:Математика 1 класс. Уравнения Решение уравнений вида а + х = bСкачать

Начальные классы. Уравнения.

С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:

И одно число решили спрятать:

Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.

В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.

Неизвестное число обозначают маленькими латинскими буквами

или любой другой буквой.

И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.

При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.

Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.

Решение записывается так:

Корень пишем на следующей строке и подчеркиваем прямой линией.

Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.

Решим еще одно уравнение:

Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:

Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 68

Видео:РЕШЕНИЕ УРАВНЕНИЙ ЛЕГКО ! 1 КЛАСС МАТЕМАТИКА УРАВНЕНИЯ - ПЕТЕРСОН / ОБЪЯСНЕНИЕ КАК РЕШАТЬ УРАВНЕНИЯСкачать

Методика изучения уравнений и способов их решения.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Методика изучения уравнений и способов их решения.

Уравнение в начальном курсе математики трактуется как равенство, содержащее букву (переменную). Решить уравнение — значит узнать, при каких значениях буквы (переменной) уравнение обращается в верное числовое равенство. Значение переменной, при котором уравнение обращается в верное числовое равенство, называют решением уравнения.

В учебнике М.И. Моро учащиеся решают уравнения двумя способами: 1) способом подбора (в простейших случаях); 2) способом, основанном на применении правил нахождения неизвестных компонентов арифметических действий.

В методике формирования у младших школьников представлений об уравнении можно выделить следующие этапы:

I этап – подготовительный. На этом этапе выполняются следующие два вида упражнений: 1) решаются способом подбора примеры с «окошком» вида  + 3 = 7;  — 4 = 2; 8 —  = 5;

2) раскрывается связь между компонентами и результатом действий сложения и вычитания (правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого).

Выполнение специальных упражнений – равенств с «окошками» является подготовкой для перехода к решению простейших уравнений вида х + 2 = 7; х — 5 = 4; 8 — х = 6, с которыми учащиеся знакомятся только во 2 классе (часть 1, с.68).

II этап – знакомство с уравнением и овладение способом его решения.

Введение понятия «уравнение» фактически сводится к замене «окошка» латинской буквой х и к введению термина «неизвестное число».

Ознакомление с уравнением можно начать с рассмотрением равенства с «окошком»:  + 4 = 7

К какому числу надо прибавить 4, чтобы получилось 7?

(Вместо «окошка» учащиеся подставляют одно за другим числа 0, 1, 2, 3, пока не найдут такое, которое подходит, чтобы получилось верное равенство).

Учитель объясняет, что в математике принято обозначать неизвестное число латинской буквой х (вставляет х в окошко).

х + 4 = 7 – это уравнение.

Решить уравнение – значит найти неизвестное число.

Чему равно неизвестное число в данном уравнении? (3).

На данном этапе очень важно сформировать осознанный и математически верный подход к решению уравнений, чтобы ученик сразу ориентировался на то, что подобранное им число он должен проверить, т.е. подставить его и выяснить, верное или неверное числовое равенство при этом получится.

Сначала уравнения решаются способом подбора (учащиеся могут при этом воспользоваться как знанием состава числа, так и вычислительными приемами сложения или вычитания в пределах 10).

Используя способ подбора, учащиеся смогут справиться и с решением уравнений на нахождение неизвестного уменьшаемого или вычитаемого. Например, 9 – х = 7. (Подставим вместо х один: 9 — 1  7, х  1; подставим число 2: 9 – 2 = 7, х = 2).

Аналогично в 3 классе вводятся уравнения вида х • 3 = 12, 5 • х = 10, х : 2 = 4, 6 : х = 3, которые также вначале решаются подбором с использованием табличных случаев умножения и деления.

Позднее, когда учащиеся усвоят знания связей между компонентами и результатами арифметических действий уравнения начинают решать на основе знаний правил нахождения неизвестного компонента.

Для решения уравнений вторым способом с помощью правила предлагается такое уравнение, которое дети не могут быстро решить способом подбора, например: х + 13 = 71.

Решение уравнения оформляется следующим образом:

х + 13 = 71 х — 5 = 27 32 — х = 8

х = 71 — 13 х = 27 + 5 х = 32 — 8

58 + 13 = 71 32 — 5 = 27 32 — 24 = 8

71 = 71 27 = 27 8 = 8

14 • х = 28 х : 6 = 12 48 : х = 4

х = 28 : 14 х = 12 • 6 х = 48 : 4

14 • 2 = 28 72 : 6 = 12 48 : 12 = 4

28 = 28 12 = 12 4 = 4

Ученики объясняют решение уравнения х + 13 = 71 так: читаю уравнение х плюс 13 равно 71 (сумма чисел х и 13 равна 71; х увеличить на 13 получится 71). В уравнении неизвестно первое слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть второе слагаемое. Из 71 вычтем 13, получим 58. Значит, х равен 58. Проверим: к 58 прибавим 13, получим 71. Получилось верное равенство 71 = 71, значит уравнение решено правильно .( 3 кл. ч 2 с. 20- объяснить самост)

Особенности ознакомления с уравнениями в курсе Л.Г. Петерсон

В 1 классе (часть 3, уроки 11 — 18) решаются уравнения на сложение и вычитание с фигурами, линиями и числами на основе взаимосвязи между частью и целым. Для решения этих уравнений достаточно применить уже известные учащимся правила:

Целое равно сумме частей.

Чтобы найти часть надо из целого вычесть другую часть.

На уроке 11 вводится понятие уравнения. Перед этим в устные упражнения целесообразно включать примеры с «окошками», решаемые на основе взаимосвязи «часть — целое»:

Затем рассматриваются способ решения уравнений на основе понятий «целое» и «части»:

1) х + 4 = 8 х и 4 — части, 8 — целое.

х = 8 — 4 Ищем часть, поэтому из целого вычитаем другую часть.

Во втором классе во второй части (урок 1) рассматриваются уравнений нового вида с умножением и делением (а • х = b , х : а = b , а : х = b .)

Учащиеся знакомятся еще с новым способом решения таких уравнений на основе правил на нахождение стороны и площади прямоугольника.

Для решения уравнений данного вида нельзя использовать правила о части и целом, так как второй множитель ( х • 4 = 12 ) — это не часть, а количество равных частей, на которое разбито целое.

В 3 классе (часть 1, урок 10) дается определение уравнения и корня уравнения; показывается решение уравнений на основе правил нахождения неизвестных компонентов действий:

— Если в равенство, содержащее переменную, подставить какое-нибудь число, то может получиться верное или неверное высказывание. Например, при x = 3 равенство x + 2 = 5 будет верным, а при x = 8 — неверным.

— Уравнением называют равенство, содержащее переменную, значение которой надо найти.

— Значение переменной, при котором из уравнения получается верное равенство, называют корнем уравнения. Решить уравнение — значит найти все его корни (или убедиться, что их нет).

Неизвестно слагаемое. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

Неизвестно уменьшаемое. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Неизвестно вычитаемое. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Неизвестен множитель. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Неизвестно делимое. Чтобы найти неизвестное делимое, надо делитель умножить на частное.

Неизвестен делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Затем решаются уравнения более сложной структуры, которые после упрощения числовых выражений в правой части, сводятся к известным случаям: (х + 3) : 8 = 5.При решении таких уравнений рассуждаем так: 1) последнее действие – деление, значит задано частное. 2) неизвестное в делимом, чтобы найти неизвестное делимое, надо частное умножить на делитель: х + 3 = 5 ∙ 8; х + 3 = 40.

3) получили сумму, неизвестно первое слагаемое, чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое: х = 40 – 3; х = 37. Проверка: (37 + 3) : 8 = 5; 5 = 5.