Уравнение длинных линий в гиперболических функциях (6 видео)

Гиперболическая форма уравнений длинной линии

Гиперболическая форма уравнений длинной линии (ДЛ) имеет следующий вид (после применения формул Эйлера для решения уравнений длинной линии с использованием падающей и отраженной волн)

U ( x ) = U 2 c h γ x + I 2 Z В s h γ x ; I ( x ) = U 2 Z В s h γ x + I 2 c h γ x ,

что соответствует гиперболической форме уравнений симметричного четырехполюсника

U 1 = U 2 c h γ + I ′ 2 Z C s h γ ; I 1 = U 2 Z C s h γ + I ′ 2 c h γ .

Поскольку I’₂ соответствует току I₂ ДЛ, волновое сопротивление Z_B = Z_C соответствует характеристическому сопротивлению четырехполюсника, а характеристическая мера передачи четырехполюсника γ соответствует γ·l.

Здесь l – длина длинной линии; x – координата длинной линии, отсчитанная от ее конца (нагрузки); U₁, I₁ и U₂, I₂ – переменные входа и выхода длинной линии.

Таким образом, длинной линии – симметричный четырехполюсник.

Гиперболическая форма уравнений, длинная линия

Содержание

Уравнение длинных линий в гиперболических функциях
Рисунок 3. Ценная линия и расчётная схема.
Гиперболические функции
Гиперболические функции
Свойства гиперболических функций
Дифференцирование и интегрирование гиперболических функций
Переход от гиперболических функций к тригонометрическим и наоборот
💥 Видео

Видео:Основы радиочастотной электроники. Лекция 1. Теория длинных линийСкачать

Уравнение длинных линий в гиперболических функциях

Кривая, форма которой соответствует однородной гибкой нерастяжимой тяжелой нити, закрепленной с обоих концов и находящейся под действием силы тяжести, называется цепной линией. Очевидно, цепная линия является плоской кривой, то есть такой кривой, все точки которой лежат в одной плоскости.

Долгое время считалось, что цепная линия представляет собой параболу, подобно тому, как траектория движения камня в поле земного тяготения есть парабола. Однако уже в начале 17 века великий итальянский мыслитель Галилео Галилей высказал предположения, что цепная линия не является параболой. Строгое решение задачи с выводом уравнения цепной линии впервые было найдено в трудах великих немецких мыслителей Готфрида Лейбница и Иоганна Бернулли, а также великого нидерландского естествоиспытателя Христиана Гюйгенса в 1691 году.

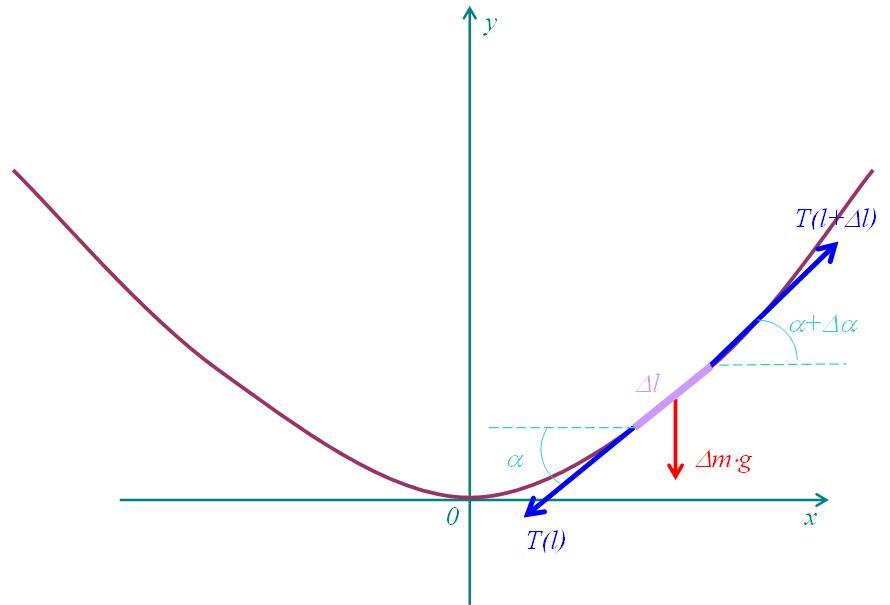
Рассмотрим элементарный участок нити длиной (Delta l) (Рисунок 3). Масса этого участка равна (Delta m = rho S Delta l) и на него действуют распределенная по длине сила тяжести интенсивности (rho gS), направленная вниз и равная (Delta m g = rho g S Delta l). Здесь (rho) — объемная плотность материала нити, (g) — ускорение свободного падения, (S) — площадь поперечного сечения нити.

Также на концах данного участка действуют силы натяжения (T(l)) и (T(l+Delta l)).

Рисунок 1. Цепи, используемые при штабелирование парахода “Бремен”. Фото из Федерального архива Германии.
Bundesarchiv Bild 102-06406, Bremen, Stapellauf des Dampfers «Bremen».

Рисунок 2. Цепи ограждения Царь-пушки в московском кремле. http://www.fotokonkurs.ru/photo/58515

Условие равновесия рассматриваемого участка запишется в виде: $$ vec T(l) + vec T(l+Delta l) + Delta mvec g = 0. $$ В проекции на оси координат получим $$ — T(l)cos(alpha) + T(l+Delta l)cos(alpha + Delta alpha) = 0. $$ $$ — T(l)sin(alpha) + T(l+Delta l)sin(alpha + Delta alpha) — rho gSDelta l = 0.$$ Из первого уравнения получаем, что горизонтальная компонента силы натяжения (T(l)) всегда постоянна: ( T(l)cosalpha(l) = T_0 = const.) Второе уравнение перепишем в виде: $$ d(T(l)sin(alpha(l)) = d(rho gSl).$$ С учётом сказанного, можем записать $$ T_0 d(tg(alpha(l)) = rho gSdl).$$ Памятуя о геометрическом смысле производной, запишем (tgalpha = y’) и тогда получим $$frac
= frac.$$ Переходя к переменной x, используя правило дифференцирования сложной функции и выражение для дифференциала дуги кривой, получим $$frac
= frac cdot frac
= frac cdot frac<dx cdot sqrt> = $$ $$ = frac cdot frac <sqrt> = frac .$$ Отсюда, учитывая, что производная от первой производной есть вторая производная, получаем $$y» = frac cdot sqrt.$$
Последнее уравнение называется дифференциальным уравнением цепной линии. Это уравнение второго порядка, допускающее понижение порядка. Чтобы понизить порядок уравнения сделаем замену (z(x)=y’). Тогда (y»=z’). Подставляя в последнее дифференциальное уравнение, получим $$frac = z’ frac cdot sqrt.$$

Рисунок 3. Ценная линия и расчётная схема.

Получили уравнение с разделяющимися переменными, которое после элементарных преобразований принимает вид $$frac<sqrt> = frac cdot dx.$$ Интегрируем последнее уравнение $$intfrac<sqrt> = frac int dx,$$ $$ln|z + sqrt| = frac cdot x + C_1.$$ Принимая за начало координат нижнюю точку цепной линии, заметим, что касательная в нижней точке горизонтальная, другими словами, нижняя точка является точкой экстремума для функции (y(x)). Следовательно, (y’(0)=z(0)=0). Подставим в последнее выражение (x=0, y=0, z=0). В результате получим (С_1 = 0). Тогда уравнение цепной линии перепишется в виде $$ln|z + sqrt| = frac cdot x.$$ Потенцируя полученное уравнение, перепишем его в показательной форме

Здесь для сокращения записи мы ввели обозначение (frac = kappa.)
Умножим обе части уравнение (1) на выражение сопряжённое к левой части (z-sqrt). Получим $$(z + sqrt)cdot(z — sqrt) = e^cdot(z — sqrt).$$ Нетрудно заметить, что $$(z + sqrt)cdot(z — sqrt) = z^2 — (sqrt)^2 = z^2 -1 + z^2 = -1.$$ Вследствие последнего замечания, уравнение можно переписать в виде $$e^cdot(z — sqrt) = -1.$$ или в виде $$z — sqrt = -e^. $$ Прибавим последнее выражением к выражению (1), и поделим полученное равенство на 2. В результате получим $$z = frac <e^- e^>. $$ Определение 1. Гиперболическим синусом от (x) называется функция, определённая следующим выражением $$sh(x) = frac <e^- e^>. $$ Определение 2. Гиперболическим косинусом от (x) называется функция, определённая следующим выражением $$sh(x) = frac <e^+ e^>. $$ Предложение 1. Производная от гиперболического косинуса есть гиперболический синус, производная от гиперболического синуса есть гиперболический косинус, то есть$$sh'(x) = ch(x),$$ $$ch'(x) = sh(x).$$ Доказательство. $$sh'(x) = left(frac <e^- e^>right)’ = frac <(e^- e^)’> = frac <(e^)’ — (e^)’> = frac <(e^)’ + (e^)’> = ch(x);$$ $$ch'(x) = left(frac <e^+ e^>right)’ = frac <(e^+ e^)’> = frac <(e^)’ + (e^)’> = frac <(e^)’ — (e^)’> = sh(x).$$ Доказательство завершено. ❑

Следствие 1. Первообразная от гиперболического косинуса есть гиперболический синус, а первообразная от гиперболического синуса есть гиперболический косинус.

Следствие 2. $$int sh(x)dx = ch(x) + C, $$ $$ int ch(x)dx = sh(x) + C.$$
С учётом сформулированных определений, а также памятуя о сделанной ранее замене (z(x)), перепишем выражение для прогиба в следующем виде $$ y’ = z = frac <e^- e^> = sh(kappa x).$$
На основании предложения 1 и следствий к нему, после интегрирования получим $$ y(x) = int sh(kappa x)dx = frac cdot ch(kappa x) + C.$$
В принятой системе координат, когда нижняя точка цепной линии является началом системы координат, справедливо следующее начальное условие (y(0)=0). Подставим это условие в найденное уравнение цепной линии и получим $$ y(0) = frac + C = 0,$$ $$ frac cdot frac +C = frac cdot frac +C = frac + C = 0. $$ Отсюда (С=-frac ) и уравнение цепной линии запишется в виде $$ y(x) = frac left(ch(kappa x) — 1right).$$
Таким образом, форма цепной линии определяется как гиперболический косинус с параметром (kappa). Кроме гиперболического синуса и гиперболического косинуса существуют также гиперболический тангенс и котангенс, которые определяются по тому же принципу, что и тригонометрический тангенс и котангенс, а именно:

Определение 3. Гиперболическим тангенсом от (x) называется функция, определённая следующим выражением $$th(x) = frac .$$
Определение 4. Гиперболическим котангенсом от (x) называется функция, определённая как частное гиперболического скосинуса и гиперболического синуса. То есть гиперболический котангенс это функция, определённая следующим выражением $$cth(x) = frac .$$
Из сделанных определений следуют равенства $$th(x) cdot cth(x) = 1;$$ $$th(x) =frac <e^x — e^><e^x + e^>;$$ $$cth(x) =frac <e^x + e^><e^x — e^>.$$
Исследуем ряд других замечательных свойств гиперболических функций.

Предложение 2. Справедливы следующие тождества $$сh^2(x) — sh^2(x) = 1;$$ $$1-th^2(x) = frac ,$$ $$cth^2(x) — 1 = frac .$$ Доказательство.

Из определений гиперболического косинуса и гиперболического синуса следует: $$ch^2(x) — sh^2(x) = left(frac <e^+ e^>right)^2 — left(frac <(e^- e^)>right)^2 = $$ $$ = frac <(e^)^2 + 2e^xe^ + (e^)^2> — frac <(e^)^2 — 2e^xe^ + (e^)^2> = e^xe^ = e^ = e^0 = 1.$$ Первое тождество доказано. Из него следует $$ch^2(x) = 1 + sh^2(x);$$ $$sh^2(x) = ch^2(x) — 1.$$ Тогда $$1 — th^2(x) = 1 — frac = frac = frac .$$ $$cth^2(x) — 1 = frac — 1 = frac = frac .$$ Все три тождества доказаны. ❑

Задание.
Найти производные гиперболического тангенса и гиперболического котангенса.

Решение.
По правилу дифференцирования частного, получим для производной гиперболического тангенса $$th'(x) = left(fracright)’ = frac = $$ $$ = frac = frac = frac .$$
Аналогично получим производную для функции гиперболический котангенс $$cth'(x) = left(fracright)’ = frac = $$ $$ = frac = frac = — frac .$$
Таким образом, мы доказали следующие соотношения $$ th'(x) = frac ;$$ $$ cth'(x) = — frac .$$
Обратим внимание на некоторое сходство полученных тождеств с соответствующими тригонометрическими тождествами.

Видео:Длинные линии │Цепи с распределенными параметрами │Теория, часть 1Скачать

Гиперболические функции

Содержание:

Видео:Лекция 185. Уравнения для длинных линийСкачать

Гиперболические функции

Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Основные понятия:

Рассмотрим единичную окружность с центром в начале координат, уравнение которого имеет вид х 2 + у 2 = 1.

Согласно определению, синусом угла называют ординату у точки А(х, у) единичной окружности, а косинусом — абсциссу х этой же точки (рис. 1)

Докажем, что площадь сектора АОВ равна числовому значению угла AOD, взятом в радианах.

Действительно, если R=1, а угол сектора АОВ- то

Следовательно, в тригонометрических функциях за аргумент можно принимать не только угол, а и площадь соответствующего сектора.

Рассмотрим теперь равнобокую гиперболу с асимптотами , уравнение которой имеет вид

Повторим предыдущие рассуждения:

— выберем на гиперболе т. А(х, у);

— проведём радиусы ОА и ОВ ().

Образовавшуюся фигуру OANB называют гиперболическим сектором (сектором ),

абсциссу точки А — гиперболическим косинусом;

ординату точки А — гиперболическим синусом.

Возьмём за аргумент площадь гиперболического сектора . Получим:

Найдём площадь гиперболического сектора, как разность площади треугольника АОВ и криволинейной трапеции ANB.

Потому, что фигура симметрична, имеем

либо, решив систему

Аналогично как в тригонометрии вводят понятия тангенса и котангенса

Свойства гиперболических функций

Чётность и нечётность проверим подставив (-х) в соответствующие формулы

Следовательно, как и в тригонометрических функциях, имеем чётная, а нечётные.

Остальные свойства легко установить построив графики гиперболических функций.

Для построения воспользуемся записью

то есть графики функций

Полученные графическим сложением ординат графики функций имеют вид:

Графики следующие

Видим, что в отличии от тригонометрических, гиперболические функции непериодические. Основные свойства каждой из гиперболических функций указаны в опорном конспекте (п. 10.5).

Дифференцирование и интегрирование гиперболических функций

Гиперболические функции можно дифференцировать и интегрировать. Выведем формулы производных и интегралов.

Переход от гиперболических функций к тригонометрическим и наоборот

Используя гиперболические функции можно вывести формулы Эйлера. Действительно, вспомним разложение в ряд Маклорена функций

Положим в разложении функции у=е х за аргумент х=zj. Получим:

Учитывая, что где будем иметь:

Именно эти формулы позволяют установить зависимость между тригонометрическими и гиперболическими функциями.

Принимаем без доказательств, что все тригонометрические формулы действительны и для воображаемого аргумента. Это предположение позволит установить зависимость между гиперболическими функциями.

Аналогично можно получить формулы для

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.