Уравнение дирака феномен квантовой запутанности

Данная статья посвящена работе Поля Дирака, уравнение которого значительно обогатило квантовую механику. Она описывает основные понятия, необходимые для того, чтобы разобраться в физическом смысле уравнения, а также способы его применения.

Видео:❓ Тайна Квантовой ЗапутанностиСкачать

Наука и ученые

Человек, не связанный с наукой, представляет процесс добычи знаний каким-то магическим действием. А ученые, по мнению таких людей, — это чудаки, которые говорят на непонятном языке и слегка высокомерны. Знакомясь с исследователем, далекий от науки человек сразу говорит, что он в школе физику не понимал. Таким образом обыватель отгораживается от научного знания и просит более образованного собеседника говорить проще и понятнее. Наверняка Поля Дирака, уравнение которого мы рассматриваем, приветствовали так же.

Видео:Квантовая формула любвиСкачать

Элементарные частицы

Строение вещества всегда волновало любознательные умы. В Древней Греции люди заметили, что мраморные ступени, по которым прошло множество ног, со временем меняют форму, и предположили: каждая ступня или сандалия уносила с собой крошечную частицу вещества. Эти элементы решили назвать «атомами», то есть «неделимыми». Наименование осталось, но выяснилось, что и атомы, и частицы, из которых состоят атомы, — тоже составные, сложные. Эти частицы называются элементарными. Именно им посвящена работа Дирака, уравнение которого позволило не только объяснить спин электрона, но и предположить наличие антиэлектрона.

Видео:▽ Квантовая запутанность(что такое квантовая запутанность)Скачать

Корпускулярно-волновой дуализм

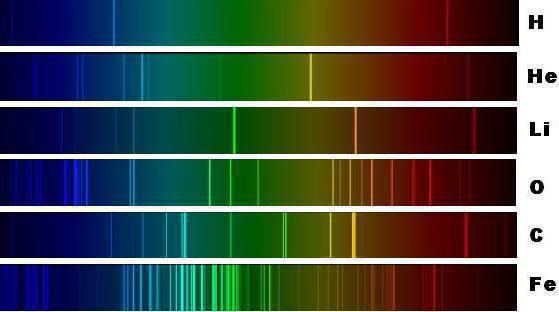
Развитие техники фотографии в конце девятнадцатого века повлекло за собой не только моду на запечатление себя, еды и кошек, но и продвинуло возможности науки. Получив такой удобный инструмент, как быстрая фотография (напомним, раньше выдержки доходили до 30-40 минут), ученые стали массово фиксировать разнообразные спектры.

Существующие на тот момент теории строения веществ не могли однозначно объяснить или предсказать спектры сложных молекул. Сначала знаменитый опыт Резерфорда доказал, что атом не такой уж неделимый: в его центре находилось тяжелое положительное ядро, вокруг которого располагались легкие отрицательные электроны. Потом открытие радиоактивности доказало, что и ядро не монолит, а состоит из протонов и нейтронов. А дальше почти одновременное открытие кванта энергии, принципа неопределенности Гейзенберга и вероятностной природы местоположения элементарных частиц дали толчок к развитию принципиально иного научного подхода к изучению окружающего мира. Появился новый раздел – физика элементарных частиц.

Основным вопросом на заре этого века великих открытий в сверхмалых масштабах стало объяснение наличия у элементарных частиц и массы, и свойств волны.

Эйнштейн доказал, что даже неуловимый фотон обладает массой, так как передает импульс твердому телу, на который падает (явление давления света). При этом многочисленные опыты по рассеянию электронов на щелях говорили как минимум о наличии у них дифракции и интерференции, это свойственно только волне. В итоге пришлось признать: элементарные частицы одновременно и объект с массой, и волна. То есть масса, скажем, электрона как бы «размазана» в пакет энергии с волновыми свойствами. Этот принцип корпускулярно-волнового дуализма позволил объяснить прежде всего, почему электрон не падает на ядро, а также по каким причинам в атоме существуют орбиты, а переходы между ними скачкообразные. Эти переходы и порождают спектр, уникальный для любого вещества. Далее физика элементарных частиц должна была объяснить свойства самих частиц, а также их взаимодействие.

Видео:Квантовая запутанность или «жуткое взаимодействие» [Veritasium]Скачать

Волновая функция и квантовые числа

Эрвин Шредингер совершил удивительное и до сих пор малопонятное открытие (на его основании чуть позже Поль Дирак построил свою теорию). Он доказал, что состояние любой элементарной частицы, например, электрона описывает волновая функция ψ. Сама по себе она ничего не значит, а вот ее квадрат покажет вероятность найти электрон в данном месте пространства. При этом состояние элементарной частицы в атоме (или другой системе) описывается четырьмя квантовыми числами. Это главное (n), орбитальное (l), магнитное (m) и спиновое (m_s) числа. Они показывают свойства элементарной частицы. Как аналогию можно привести брусок масла. Его характеристики – масса, размер, цвет и жирность. Однако свойства, описывающие элементарные частицы, нельзя понять интуитивно, их надо осознавать через математическое описание. Работа Дирака, уравнение которого — в центре внимания этой статьи, посвящена последнему, спиновому числу.

Прежде чем перейти непосредственно к уравнению, необходимо объяснить, что же обозначает спиновое число m_s. Оно показывает собственный момент импульса электрона и других элементарных частиц. Это число всегда положительно и может принимать целое значение, ноль или полуцелое значение (для электрона m_s = 1/2). Спин – величина векторная и единственная, которая описывает ориентацию электрона. Квантовая теория поля кладет спин в основу обменного взаимодействия, которому нет никакого аналога в обычно интуитивно понятной механике. Спиновое число показывает, каким образом должен повернуться вектор, чтобы прийти в изначальное состояние. Примером может служить обычная шариковая ручка (пишущая часть пусть будет положительным направлением вектора). Чтобы она пришла в изначальное состояние, ее надо повернуть на 360 градусов. Такая ситуация соответствует спину, равному 1. При спине 1/2, как у электрона, поворот должен быть 720 градусов. Так что, помимо математического чутья, надо иметь развитое пространственное мышление, чтобы понять это свойство. Чуть выше шла речь о волновой функции. Она является основным «действующим лицом» уравнения Шредингера, с помощью которого описывается состояние и положение элементарной частицы. Но это соотношение в своем изначальном виде предназначено для частиц без спина. Описать состояние электрона можно, только если провести обобщение уравнения Шредингера, что и было проделано в работе Дирака.

Видео:Что не так с квантовой запутанностью? Квантовые эффекты простым языком!Скачать

Бозоны и фермионы

Фермион – частица с полуцелым значением спина. Фермионы располагаются в системах (например атомах) согласно принципу Паули: в каждом состоянии должно быть не более одной частицы. Таким образом, в атоме каждый электрон чем-то отличается от всех остальных (какое-то квантовое число имеет другое значение). Квантовая теория поля описывает и другой случай – бозоны. Они имеют целый спин и могут все одновременно быть в одном состоянии. Реализация этого случая называет Бозе-конденсацией. Несмотря на достаточно хорошо подтвержденную теоретическую возможность его получить, практически это осуществили только в 1995 году.

Видео:🧪🧪🧪🧪Квантовая запутанность. Нобелевская по физике 2022.Скачать

Уравнение Дирака

Как мы уже говорили выше, Поль Дирак вывел уравнение классического поля электрона. Оно также описывает состояния других фермионов. Физический смысл соотношения сложен и многогранен, и из его формы следует много фундаментальных выводов. Вид уравнения следующий:

где m — масса фермиона (в частности электрона), с — скорость света, p_k— три оператора компонент импульса (по осям x, y, z), ħ — урезанная постоянная Планка, x и t – три пространственные координаты (соответствуют осям X, Y, Z) и время, соответственно, и ψ(x, t) — четырёхкомпонентная комплексная волновая функция, α_k (k=0, 1, 2, 3) — матрицы Паули. Последние представляют собой линейные операторы, которые действуют на волновую функцию и ее пространство. Формула эта довольно сложная. Чтобы понять хотя бы ее компоненты, надо разбираться в основных определениях квантовой механики. Также следует обладать недюжинными математическими познаниями, чтобы как минимум знать, что такое вектор, матрица и оператор. Специалисту вид уравнения скажет еще больше, чем его компоненты. Человек, сведущий в ядерной физике и знакомый с квантовой механикой, поймет важность этого соотношения. Однако надо признаться, что уравнения Дирака и Шредингера — всего лишь элементарные основы математического описания процессов, которые происходят в мире квантовых величин. Физики-теоретики, которые решили посвятить себя элементарным частицам и их взаимодействию, должны понимать суть этих соотношений на первом-втором курсах института. Но наука эта увлекательная, и именно в этой области можно совершить прорыв или увековечить свое имя, присвоив его уравнению, преобразованию или свойству.

Видео:История создания квантовой механики #5: Шредингер и ДиракСкачать

Физический смысл уравнения

Как мы и обещали, рассказываем, какие выводы таит уравнение Дирака для электрона. Во-первых, из этого соотношения становится ясно, что спин электрона равен ½. Во-вторых, согласно уравнению, у электрона есть собственный магнитный момент. Он равен магнетону Бора (единица элементарного магнитного момента). Но самый главный результат получения этого соотношения кроется в незаметном операторе α_k. Вывод уравнения Дирака из уравнения Шредингера занял много времени. Вначале Дирак думал, что эти операторы мешают соотношению. С помощью разных математических ухищрений он пытался исключить их из уравнения, но ему это не удалось. В итоге уравнение Дирака для свободной частицы содержит четыре оператора α. Каждый из них представляет собой матрицу [4×4]. Два соответствуют положительной массе электрона, что доказывает наличие двух положений его спина. Другие же два дают решение для отрицательной массы частицы. Самые простые познания в физике предоставляют человеку возможность заключить, что это невозможно в реальности. Но в результате эксперимента выяснилось, что последние две матрицы являются решениями для существующей частицы, противоположной электрону – антиэлектрону. Как и электрон, позитрон (так назвали эту частицу) обладает массой, но его заряд положителен.

Видео:КВАНТОВАЯ ЗАПУТАННОСТЬ ИЛИ ЗА ЧТО ВРУЧИЛИ НОБЕЛЕВСКУЮ ПРЕМИЮ?Скачать

Позитрон

Как часто бывало в эру квантовых открытий, Дирак сначала не поверил собственному выводу. Он не решился открыто опубликовать предсказание новой частицы. Правда, во множестве статей и на различных симпозиумах ученый подчеркивал возможность ее существования, хотя и не постулировал это. Но вскоре после вывода этого знаменитого соотношения позитрон был найден в составе космического излучения. Таким образом, его существование было подтверждено эмпирически. Позитрон – первый найденный людьми элемент антиматерии. Позитрон рождается как один из близнецов пары (другой близнец – это электрон) при взаимодействии фотонов очень высокой энергии с ядрами материи в сильном электрическом поле. Приводить цифры мы не будем (заинтересованный читатель и сам найдет всю нужную информацию). Однако стоит подчеркнуть, что речь идет о космических масштабах. Произвести фотоны нужной энергии способны лишь взрывы сверхновых и столкновения галактик. Также они в некотором количестве содержатся в ядрах горячих звезд, в том числе Солнца. Но человек всегда стремится к своей выгоде. Аннигиляция материи с антиматерией дает много энергии. Чтобы обуздать этот процесс и пустить его на благо человечества (например, эффективными были бы двигатели межзвездных лайнеров на аннигиляции), люди научились изготавливать протоны в лабораторных условиях.

В частности, большие ускорители (типа адронного коллайдера) могут создавать пары электрон-позитрон. Раньше также высказывались предположения, что существуют не только элементарные античастицы (помимо электрона их еще несколько), но и целая антиматерия. Даже совсем небольшой кусочек любого кристалла из антивещества обеспечил бы энергией всю планету (может быть, криптонит супермена был антиматерией?).

Но увы, создание антиматерии тяжелее ядер водорода в обозримой вселенной задокументировано не было. Однако если читатель думает, что взаимодействие вещества (подчеркнем, именно вещества, а не отдельно взятого электрона) с позитроном сразу заканчивается аннигиляцией, то он ошибается. При торможении позитрона с высокой скоростью в некоторых жидкостях с ненулевой вероятностью возникает связанная пара электрон-позитрон, которая называется позитроний. Это образование имеет некоторые свойства атома и даже способно вступать в химические реакции. Но существует этот хрупкий тандем недолго и потом все равно аннигилирует с испусканием двух, а в некоторых случаях и трех гамма-квантов.

Видео:Квантовая физика простым языком - поймут всеСкачать

Недостатки уравнения

Несмотря на то что благодаря этому соотношению был обнаружен антиэлектрон и антиматерия, оно имеет существенный недостаток. Запись уравнения и модель, построенная на его основе, не способны предсказать, как рождаются и уничтожаются частицы. Это своеобразная ирония квантового мира: теория, предсказавшая рождение пар материя-антиматерия, не способна адекватно описать этот процесс. Данный недостаток был устранен в квантовой теории поля. Путем введения квантованности полей эта модель описывает их взаимодействие, в том числе рождение и уничтожение элементарных частиц. Под «квантовой теорией поля» в данном случае подразумевается совершенно конкретный термин. Это область физики, которая изучает поведение квантовых полей.

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Уравнение Дирака в цилиндрических координатах

Для начала сообщим, что такое цилиндрическая система координат. Вместо привычных трех взаимно перпендикулярных осей для определения точного местоположения точки в пространстве используются угол, радиус и высота. Это то же самое, что полярная система координат на плоскости, только добавляется третье измерение – высота. Эта система удобна, если требуется описать или исследовать некоторую поверхность, симметричную относительно одной из осей. Для квантовой механики это весьма полезный и удобный инструмент, который позволяет значительно сократить размер формул и количество вычислений. Это следствие осесимметричности электронного облака в атоме. Уравнение Дирака в цилиндрических координатах решается несколько иначе, чем в привычной системе, и дает иногда неожиданные результаты. Например, некоторые прикладные задачи по определению поведения элементарных частиц (чаще всего электронов) в квантованном поле решались преобразованием вида уравнения к цилиндрическим координатам.

Видео:Элементарные частицы | уравнение ДиракаСкачать

Использование уравнения для определения строения частиц

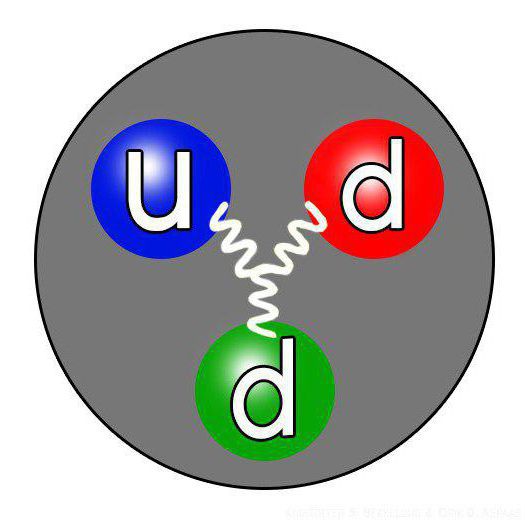
Это равенство описывает простые частицы: такие, которые не состоят из еще более мелких элементов. Современная наука способна измерять магнитные моменты с достаточно высокой точностью. Таким образом, несоответствие посчитанного с помощью уравнения Дирака значения измеренному экспериментально магнитному моменту будет косвенно свидетельствовать о сложном строении частицы. Напомним, это равенство применимо к фермионам, их спин полуцелый. С помощью этого уравнения была подтверждена сложная структура протонов и нейтронов. Каждый из них состоит из еще более мелких элементов, которые называются кварками. Глюонное поле держит кварки вместе, не давая им рассыпаться. Существует теория, что и кварки — это не самые элементарные частицы нашего мира. Но пока у людей не хватает технической мощи, чтобы это проверить.

Видео:Эксперимент, который взрывает мозг!Скачать

Просто о квантовой запутанности

Квантовая запутанность – одно из самых сложных понятий в науке, но основные её принципы просты. А если понять её, запутанность открывает путь к лучшему пониманию таких понятий, как множественность миров в квантовой теории.

Чарующей аурой загадочности окутано понятие квантовой запутанности, а также (каким-то образом) связанное с ним требование квантовой теории о необходимости наличия «многих миров». И, тем не менее, по сути своей это научные идеи с приземлённым смыслом и конкретными применениями. Я хотел бы объяснить понятия запутанности и множества миров настолько просто и ясно, насколько знаю их сам.

Запутанность считается явлением, уникальным для квантовой механики – но это не так. На самом деле, для начала будет более понятным (хотя это и необычный подход) рассмотреть простую, не квантовую (классическую) версию запутанности. Это позволит нам отделить тонкости, связанные с самой запутанностью, от других странностей квантовой теории.

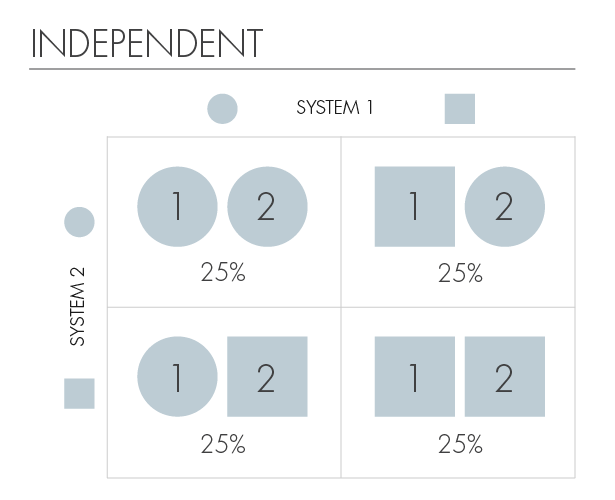
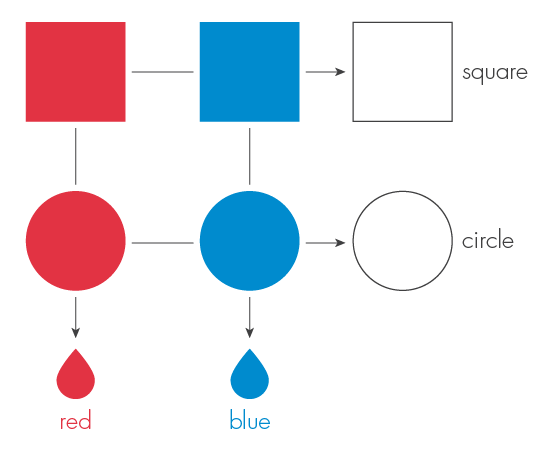
Запутанность появляется в ситуациях, в которых у нас есть частичная информация о состоянии двух систем. К примеру, нашими системами могут стать два объекта – назовём их каоны. «К» будет обозначать «классические» объекты. Но если вам очень хочется представлять себе что-то конкретное и приятное – представьте, что это пирожные.

Наши каоны будут иметь две формы, квадратную или круглую, и эти формы будут обозначать их возможные состояния. Тогда четырьмя возможными совместными состояниями двух каонов будут: (квадрат, квадрат), (квадрат, круг), (круг, квадрат), (круг, круг). В таблице указана вероятность нахождения системы в одном из четырёх перечисленных состояний.

Мы будем говорить, что каоны «независимы», если знание о состоянии одного из них не даёт нам информации о состоянии другого. И у этой таблицы есть такое свойство. Если первый каон (пирожное) квадратный, мы всё ещё не знаем форму второго. И наоборот, форма второго ничего не говорит нам о форме первого.

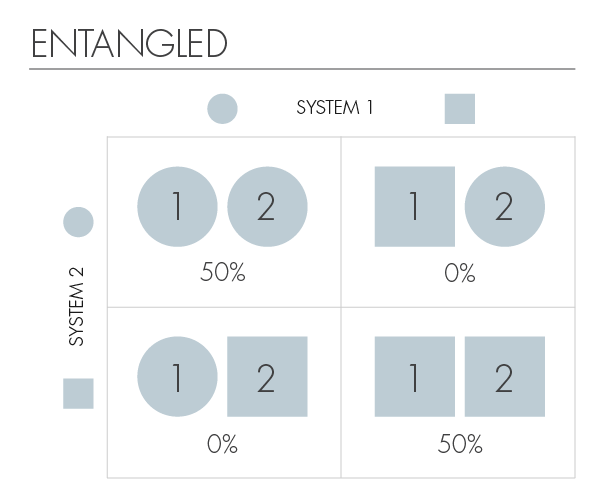
С другой стороны, мы скажем, что два каона запутаны, если информация об одном из них улучшает наши знания о другом. Вторая табличка покажет нам сильную запутанность. В этом случае, если первый каон будет круглым, мы будем знать, что второй тоже круглый. А если первый каон квадратный, то таким же будет и второй. Зная форму одного, мы однозначно определим форму другого.

Квантовая версия запутанности выглядит, по сути, также – это отсутствие независимости. В квантовой теории состояния описываются математическими объектами под названием волновая функция. Правила, объединяющие волновые функции с физическими возможностями, порождают очень интересные сложности, которые мы обсудим позже, но основное понятие о запутанном знании, которое мы продемонстрировали для классического случая, остаётся тем же.

Хотя пирожные нельзя считать квантовыми системами, запутанность квантовых систем возникает естественным путём – например, после столкновений частиц. На практике незапутанные (независимые) состояния можно считать редкими исключениями, поскольку при взаимодействии систем между ними возникают корреляции.

Рассмотрим, к примеру, молекулы. Они состоят из подсистем – конкретно, электронов и ядер. Минимальное энергетическое состояние молекулы, в котором она обычно и находится, представляет собой сильно запутанное состояние электронов и ядра, поскольку расположение этих составляющих частиц никак не будет независимым. При движении ядра электрон движется с ним.

Вернёмся к нашему примеру. Если мы запишем Φ■, Φ● как волновые функции, описывающие систему 1 в её квадратных или круглых состояниях и ψ■, ψ● для волновых функций, описывающих систему 2 в её квадратных или круглых состояниях, тогда в нашем рабочем примере все состояния можно описать, как:

Независимые: Φ■ ψ■ + Φ■ ψ● + Φ● ψ■ + Φ● ψ●

Запутанные: Φ■ ψ■ + Φ● ψ●

Независимую версию также можно записать, как:

Отметим, как в последнем случае скобки чётко разделяют первую и вторую системы на независимые части.

Существует множество способов создания запутанных состояний. Один из них – измерить составную систему, дающую вам частичную информацию. Можно узнать, например, что две системы договорились быть одной формы, не зная при этом, какую именно форму они выбрали. Это понятие станет важным чуть позже.

Более характерные последствия квантовой запутанности, такие, как эффекты Эйнштейна-Подольского-Розена (EPR) и Гринберга-Хорна-Зейлингера (GHZ), возникают из-за её взаимодействия ещё с одним свойством квантовой теории под названием «принцип дополнительности». Для обсуждения EPR и GHZ позвольте мне сначала представить вам этот принцип.

До этого момента мы представляли, что каоны бывают двух форм (квадратные и круглые). Теперь представим, что ещё они бывают двух цветов – красного и синего. Рассматривая классические системы, например, пирожные, это дополнительное свойство означало бы, что каон может существовать в одном из четырёх возможных состояний: красный квадрат, красный круг, синий квадрат и синий круг.

Но квантовые пирожные – квантожные… Или квантоны… Ведут себя совсем по-другому. То, что квантон в каких-то ситуациях может обладать разной формой и цветом не обязательно означает, что он одновременно обладает как формой, так и цветом. Фактически, здравый смысл, которого требовал Эйнштейн от физической реальности, не соответствует экспериментальным фактам, что мы скоро увидим.

Мы можем измерить форму квантона, но при этом мы потеряем всю информацию о его цвете. Или мы можем измерить цвет, но потеряем информацию о его форме. Согласно квантовой теории, мы не можем одновременно измерить и форму и цвет. Ничей взгляд на квантовую реальность не обладает полнотой; приходится принимать во внимание множество разных и взаимоисключающих картин, у каждой из которых есть своё неполное представление о происходящем. Это и есть суть принципа дополнительности, такая, как её сформулировал Нильс Бор.

В результате квантовая теория заставляет нас быть осмотрительными в приписывании свойствам физической реальности. Во избежание противоречий приходится признать, что:

Не существует свойства, если его не измерили.
Измерение – активный процесс, изменяющий измеряемую систему

Теперь опишем две образцовые, но не классические, иллюстрации странностей квантовой теории. Обе были проверены в строгих экспериментах (в реальных экспериментах люди меряют не формы и цвета пирожных, а угловые моменты электронов).

Альберт Эйнштейн, Борис Подольский и Натан Розен (EPR) описали удивительный эффект, возникающий при запутанности двух квантовых систем. EPR-эффект объединяет особую, экспериментально достижимую форму квантовой запутанности с принципом дополнительности.

EPR-пара состоит из двух квантонов, у каждого из которых можно измерить форму или цвет (но не то и другое сразу). Предположим, что у нас есть множество таких пар, все они одинаковые, и мы можем выбирать, какие измерения мы проводим над их компонентами. Если мы измерим форму одного из членов EPR-пары, мы с одинаковой вероятностью получим квадрат или круг. Если измерим цвет, то с одинаковой вероятностью получим красный или синий.

Интересные эффекты, казавшиеся EPR парадоксальными, возникают, когда мы проводим измерения обоих членов пары. Когда мы меряем цвет обоих членов, или их форму, мы обнаруживаем, что результаты всегда совпадают. То есть, если мы обнаружим, что один из них красный и затем меряем цвет второго, мы также обнаруживаем, что он красный – и т.п. С другой стороны, если мы измеряем форму одного и цвет другого, никакой корреляции не наблюдается. То есть, если первый был квадратом, то второй с одинаковой вероятностью может быть синим или красным.

Согласно квантовой теории, мы получим такие результаты, даже если две системы будет разделять огромное расстояние и измерения будут проведены почти одновременно. Выбор типа измерений в одном месте, судя по всему, влияет на состояние системы в другом месте. Это «пугающее дальнодействие», как называл его Эйнштейн, по-видимому, требует передачу информации – в нашем случае, информации о проведённом измерении – со скоростью, превышающей скорость света.

Но так ли это? Пока я не узнаю, какой результат получили вы, я не знаю, чего ожидать мне. Я получаю полезную информацию, когда я узнаю ваш результат, а не когда вы проводите измерение. И любое сообщение, содержащее полученный вами результат, необходимо передать каким-либо физическим способом, медленнее скорости света.

При дальнейшем изучении парадокс ещё больше разрушается. Давайте рассмотрим состояние второй системы, если измерение первой дало красный цвет. Если мы решим мерить цвет второго квантона, мы получим красный. Но по принципу дополнительности, если мы решим измерить его форму, когда он находится в «красном» состоянии, у нас будут равные шансы на получение квадрата или круга. Поэтому, результат EPR логически предопределён. Это просто пересказ принципа дополнительности.

Нет парадокса и в том, что удалённые события коррелируют. Ведь если мы положим одну из двух перчаток из пары в коробки и отправим их в разные концы планеты, неудивительно, что посмотрев в одну коробку, я могу определить, на какую руку предназначена другая перчатка. Точно так же, во всех случаях корреляция пар EPR должна быть зафиксирована на них, когда они находятся рядом и потому они могут выдержать последующее разделение, будто бы имея память. Странность EPR-парадокса не в самой по себе возможности корреляции, а в возможности её сохранения в виде дополнений.

Дэниел Гринбергер, Майкл Хорн и Антон Зейлингер открыли ещё один прекрасный пример квантовой запутанности. ОН включает три наших квантона, находящихся в специально подготовленном запутанном состоянии (GHZ-состоянии). Мы распределяем каждый из них разным удалённым экспериментаторам. Каждый из них выбирает, независимо и случайно, измерять ли цвет или форму и записывает результат. Эксперимент повторяют многократно, но всегда с тремя квантонами в GHZ-состоянии.

Каждый отдельно взятый экспериментатор получает случайные результаты. Измеряя форму квантона, он с равной вероятностью получает квадрат или круг; измеряя цвет квантона, он с равной вероятностью получает красный или синий. Пока всё обыденно.

Но когда экспериментаторы собираются вместе и сравнивают результаты, анализ показывает удивительный результат. Допустим, мы будем называть квадратную форму и красный цвет «добрыми», а круги и синий цвет – «злыми». Экспериментаторы обнаруживают, что если двое из них решили измерить форму, а третий – цвет, тогда либо 0, либо 2 результата измерений получаются «злыми» (т.е. круглыми или синими). Но если все трое решают измерить цвет, то либо 1 либо 3 измерения получаются злыми. Это предсказывает квантовая механика, и именно это и происходит.

Вопрос: количество зла чётное или нечётное? В разных измерениях реализовываются обе возможности. Нам приходится отказаться от этого вопроса. Не имеет смысла рассуждать о количестве зла в системе без связи с тем, как его измеряют. И это приводит к противоречиям.

Эффект GHZ, как описывает его физик Сидни Колман, это «оплеуха от квантовой механики». Он разрушает привычное, полученное из опыта ожидание того, что у физических систем есть предопределённые свойства, независимые от их измерения. Если бы это было так, то баланс доброго и злого не зависел бы от выбора типов измерений. После того, как вы примете существование GHZ-эффекта, вы его не забудете, а ваш кругозор будет расширен.

Пока что мы рассуждаем о том, как запутанность не позволяет назначить уникальные независимые состояния нескольким квантонам. Такие же рассуждения применимы к изменениям одного квантона, происходящим со временем.

Мы говорим об «запутанных историях», когда системе невозможно присвоить определённое состояние в каждый момент времени. Так же, как в традиционной запутанности мы исключаем какие-то возможности, мы можем создать и запутанные истории, проводя измерения, собирающие частичную информацию о прошлых событиях. В простейших запутанных историях у нас есть один квантон, изучаемый нами в два разных момента времени. Мы можем представить ситуацию, когда мы определяем, что форма нашего квантона оба раза была квадратной, или круглой оба раза, но при этом остаются возможными обе ситуации. Это темпоральная квантовая аналогия простейшим вариантам запутанности, описанным ранее.

Используя более сложный протокол, мы можем добавить чуть-чуть дополнительности в эту систему, и описать ситуации, вызывающие «многомировое» свойство квантовой теории. Наш квантон можно подготовить в красном состоянии, а затем измерить и получить голубое. И как в предыдущих примерах, мы не можем на постоянной основе присвоить квантону свойство цвета в промежутке между двумя измерениями; нет у него и определённой формы. Такие истории реализовывают, ограниченным, но полностью контролируемым и точным способом, интуицию, свойственную картинке множественности миров в квантовой механике. Определённое состояние может разделиться на две противоречащие друг другу исторические траектории, которые затем снова соединяются.

Эрвин Шрёдингер, основатель квантовой теории, скептически относившийся к её правильности, подчёркивал, что эволюция квантовых систем естественным образом приводит к состояниям, измерение которых может дать чрезвычайно разные результаты. Его мысленный эксперимент с «котом Шрёдингера» постулирует, как известно, квантовую неопределённость, выведенную на уровень влияния на смертность кошачьих. До измерения коту невозможно присвоить свойство жизни (или смерти). Оба, или ни одно из них, существуют вместе в потустороннем мире возможностей.

Повседневный язык плохо приспособлен для объяснения квантовой дополнительности, в частности потому, что повседневный опыт её не включает. Практические кошки взаимодействуют с окружающими молекулами воздуха, и другими предметами, совершенно по-разному, в зависимости от того, живы они или мертвы, поэтому на практике измерение проходит автоматически, и кот продолжает жить (или не жить). Но истории с запутанностью описывают квантоны, являющиеся котятами Шрёдингера. Их полное описание требует, чтобы мы принимали к рассмотрению две взаимоисключающие траектории свойств.

Контролируемая экспериментальная реализация запутанных историй – вещь деликатная, поскольку требует сбора частичной информации о квантонах. Обычные квантовые измерения обычно собирают всю информацию сразу – к примеру, определяют точную форму или точный цвет – вместо того, чтобы несколько раз получить частичную информацию. Но это можно сделать, хотя и с чрезвычайными техническими трудностями. Этим способом мы можем присвоить определённый математический и экспериментальный смысл распространению концепции «множественности миров» в квантовой теории, и продемонстрировать её реальность.

Видео:Квантовая телепортация: как не запутаться в запутанных частицах?Скачать

Квантовая запутанность

За последние полтора века произошел значительный скачок в развитии человечества, в особенности в области фундаментальной физики. Не успели ученые окунуться в физику атома, как уже начали строиться атомные станции; научный переворот, совершённый Эйнштейном в скором времени привел нас к полной глобализации с более чем тысячью спутниками на орбите Земли. Примеров – масса, однако осталось еще немало нерешенных задач и необъясненных явлений. Одно из таких явлений скрывается в микромире квантовых процессов, а именно – квантовая запутанность. Что это такое, почему это важно и какие исследования ведутся для решения этого вопроса – разбираем в данной статье.

Видео:Квантовая механика 44 - Дельта-функция ДиракаСкачать

Основные сведения

Прежде всего, определим само понятие «квантовая запутанность». Вся информация об объекте в микромире описывается неким абстрактным (математическим) состоянием, которое включает, например, вероятность обнаружения частицы в данном объеме, импульс частицы, ее заряд или спин, и тп. Подобное «состояние» может быть описано физическими уравнениями, которые, несмотря на свою абстрактность и сложность, все же способны предсказывать результаты экспериментов.

Квантовой запутанностью называют такое явление, когда квантовые состояния двух и более частиц оказываются взаимосвязаны. То есть, определив состояние одной частицы, можно предсказать некоторые характеристики другой. Примечательно, что изменение некоторого параметра одной частицы приводит к изменению некоторого параметра другой частицы, независимо от расстояния.

Видео:эффект наблюдателяСкачать

Противоречие с «принципом локальности»

Как известно из работ Эйнштейна, в природе имеет место так называемый «принцип локальности», согласно которому любое взаимодействие между телами не может происходить мгновенно, а передается через посредника. Скорость передачи этого взаимодействия не должна превышать скорость света в вакууме. В то же время, как было упомянуто ранее, квантовая запутанность может наблюдаться на огромных расстояниях с «мгновенной передачей информации», что является прямым нарушением принципа локальности.

Видео:Квантовый мир.Скачать

Эйнштейн, Нильс Бор и квантовая механика

В 1927-м году в Брюсселе состоялся Пятый Сольвеевский конгресс — международная конференция на тему актуальных проблем в области физики и химии. Одна из состоявшихся дискуссий была на тему так называемой Копенгагенской интерпретации квантовой механики.

Нильс Бор и Альберт Эйнштейн

Данная теория была разработана Нильсом Бором и Вернером Гейзенбергом и утверждает о вероятностной природе волновой функции. Несмотря на решение некоторых тогдашних проблем физики, например, связанных с корпускулярно-волновым дуализмом, данная теория также вызывала и ряд вопросов. В первую очередь, само представление объекта с известным импульсом, не имеющего определенной координаты, а лишь вероятность обнаружения в данной точке, — противоречит нашему опыту жизни в макромире. Кроме того, эта теория подразумевала неопределенность в расположении частицы, до тех пор, пока не будет произведено измерение.

Совместное фото участников Пятого Сольвеевского конгресса

Альберт Эйнштейн не мог принять такую интерпретацию, в результате чего и зародилась его известная фраза «Бог не играет в кости», на что Нильс Бор ответил «Альберт, не указывай Богу, что ему делать». Так начался длительный спор Эйнштейна и Бора.

Ответ Эйнштейна последовал в 1935-м году, когда он, вместе с Борисом Подольским и Натаном Розеном опубликовал работу, носившую название «Можно ли считать квантово-механическое описание физической реальности полным?». В данной статье был представлен мысленный эксперимент под названием «парадокс Эйнштейна — Подольского — Розена» (ЭПР-парадокс).

Видео:Параллельные миры, квантовая механика и кот [Veritasium]Скачать

ЭПР-парадокс

Эксперимент был направлен на опровержение такого фундаментального для квантовой механики утверждения, как принцип неопределенности Гейзенберга, который гласит, что нельзя одновременно измерить две характеристики частицы, зачастую имеют ввиду – импульс и координату.

ЭПР-парадокс звучит следующим образом. Пусть две частицы одного сорта образовались вследствие распада третьей частицы. Тогда сумма их импульсов будет равна импульсу исходной частицы, согласно закону сохранения импульса. Далее, зная импульс исходной частицы (которую заранее подготовят экспериментаторы), и измерив импульс второй частицы, можно рассчитать импульс первой. То есть в результате измерения мы получили такую характеристику первой частицы как импульс. Теперь измерим координату второй частицы, и в итоге будем иметь две измеренные характеристики одной частицы, что прямо противоречит принципу неопределенности Гейзенберга.

Однако в самой же квантовой механике есть средства для разрешения этого парадокса. Согласно законам квантового мира – любое измерение приводит к изменению характеристик измеряемого тела. Тогда до измерения координаты второй частицы, действительно, может иметь место определенный импульс. Но в момент измерения координаты состояние частицы меняется и нельзя утверждать, что эти характеристики были измерены одновременно.

Тем не менее, в результате корпускулярно-волнового дуализма, находясь на некотором расстоянии, эти возникшие частицы имеют состояния, описываемые одной волновой функцией. Из этого вытекает, что измерение (а значит и изменение) импульса одной частицы приводит и к измерению импульса другой. Причем увеличение расстояния между этими частицами не запрещается, что опять же противоречит принципу локальности.

Видео:Квантовая запутанность для самых маленькихСкачать

Теорема Белла

Человеку, существующему всю свою историю в масштабах макромира, сложно понять законы квантовой механики, которые часто противоречат наблюдениям в макромире. Так зародилась теория скрытых параметров, согласно которой, упомянутое ранее дальнодействие между частицами, может быть вызвано наличием неких изначально скрытых параметров частиц. Проще говоря – измерение одной частицы не приводит к изменению состояния другой, и оба эти состояния возникли вместе с этими частицами, в момент распада исходной частицы. Такое интуитивно понятное объяснение удовлетворило бы человеческий ум.

В 1964-м году Джон Стюарт Белл сформулировал свои неравенства, позже называемые теоремой, которые позволяют провести эксперимент, позволяющий точно определить – имеют ли место некие скрытые параметры. То есть если частицы имели скрытые параметры до своего разделения, то выполнилось бы одно неравенство, а если их состояния связаны и неопределенны до измерения одной из частиц – другое неравенство Белла.

В 1972-м году подобный эксперимент был проведен Фридманом и Клаузером, и результаты указывали на существования неопределенности состояний до измерения. Впрочем, данное явление воспринималось научным сообществом как некий конфуз, который рано или поздно будет разрешен. Однако в 1981-м году был нанесен второй удар по физической теории – эксперимент Аллена Аспе. Этот весьма популярный эксперимент стал последним аргументом в пользу существования квантовой запутанности и так называемого «жуткого дальнодействия». И хотя окончательно поставить точку в этом вопросе не получилось, результаты были настолько убедительны, что ученым пришлось принять такую особенность квантового мира.

Видео:Парфёнов К. В. - - Квантовая теория - Уравнение Дирака. Спиноры (Лекция 2)Скачать

Исследования в области квантовой запутанности

Почему вновь поднимается эта давно известная тема? Дело в том, что за последние несколько лет разработки в области квантовых компьютеров, работающих на основе квантовой запутанности, заметно шагнули вперед. Так в марте 2018-го года Google заявила об успешном создании 72-кубитного квантового процессора под названием Bristlecone, который достигает «квантового превосходства». То есть способен выполнять задачи, которые недоступны для обычных компьютеров.

Квантовый процессор Bristlecone компании Google (слева) и схематическое изображение кубитов, где каждый кубит связан с соседними (справа)

Также летом 2018-го года в журнале Nature была опубликована научная работа, которая рассказывает о создании первого квантового процессора с долговременной памятью. Ранее, в 2015-м году, эта же исследовательская группа из Делфтского технического университета вместе с главой организации QUTech — Рональдом Хэнсоном представили еще более убедительные доказательства существования квантовой запутанности.

Видео:В чем парадокс ЭФФЕКТА НАБЛЮДАТЕЛЯ? | Кот Шрёдингера и параллельные мирыСкачать

Об эксперименте в Делфтском техническом университете

Эксперимент, результаты которого были опубликованы в 2015-м году, происходил следующим образом. В эксперименте использовались алмазные листы с решеткой полостей, которые заполняются азотом. Такая технология была разработана исследователями Калифорнийского университета в Санта-Барбаре и Национальной лаборатории Лоуренса в Беркли в 2010-м году. Два таких кристалла алмаза расположили на расстоянии 1.3 км друг от друга. В результате облучения обоих пластин микроволновым излучением и лазерами электроны этих «алмазных ловушек» переходили в возбужденное состояние и испускали пару фотонов, которые взаимодействовали друг с другом. Как следствие этого взаимодействия – возникала квантовая запутанность между электронами, которые излучали эти фотоны.

Точки расположения алмазных листов на территории кампуса Делфтского технического университета

Для обнаружения данного явления ученые проводили измерение спинов электронов с разных пластин практически одновременно, что не допустило бы обмен информацией между ними со скоростью света. Однако, как оказалось, спины двух электронов были синхронизированы, что говорит о передачи информации неким образом, который позволяет превысить скорость света. Конечно, сама процедура определения характеристик электронов намного сложнее, и потребовалось провести немало расчетов и сравнить их волновые функции. Несмотря на все сложности эксперимента, он проводился 245 раз в течение 18-ти дней, и был запланирован таким образом, чтобы избежать всех возможных ошибок, как со стороны измерительных приборов, так и со стороны окружающей среды.

Бас Хенсен и Рональд Хэнсон устанавливают оборудование для эксперимента по проверке неравенств Белла

Окончательно закроет эту тему будущий крупный эксперимент в Массачусетском технологическом институте в течение ближайших трех лет. Исследовательская группа планирует собирать электромагнитное излучение пульсаров, а также свет, приходящий из дальних галактик. Подобный эксперимент позволит избежать какой-либо связи измерительных приборов и источников сигнала, тем самым устраняя последнюю возможность наличия скрытых параметров.

Схематическое изображение пульсара

Квантовый компьютер и интернет

Разработки QUTech вышли далеко за пределы теоретической физики и двинулись в сторону квантового компьютера. Так в 2012-м году несколько научных групп разработали двухкубитный квантовый процессор на основе вышеупомянутых кристаллов, а в 2018-м – была опубликована работа, в которой исследователи описали созданный ими квантовый процессор с долговременной памятью. Проблема создания такого процессора состояла в том, что связи между квантовыми битами («кубитами») пропадали быстрее, чем ученым удавалось их обнаружить. Очередной эксперимент в Делфтском техническом университете показал, что новый процессор не обладает данной проблемой.

Исследовательская группа использовала вышеупомянутые алмазные пластины, где среди атомов углерода «спрятался» атом азота. Место, в котором располагается атом азота, обладает специфическими свойствами, как если бы в этой ячейке кристаллической решетки находился атом углерода, но в неком «замороженном» состоянии. Такой подход заметно продлевает жизнь алмазным кубитам (300-500 миллисекунд). Кроме того, был разработан и новый метод «запутывания» электронов в этих дефектных точках.

Данная технология не только является прорывной в области квантовых компьютеров, но и приближает нас на шаг к квантовому интернету. Взаимодействие нескольких отдельных квантовых компьютеров позволит организовать между ними сеть, работающую посредством передачи запутанных кубитов. Преимущество состоит в скорости: пусть имеется k квантовых компьютеров, каждый из которых состоит из n кубитов. Тогда для передачи по обычной сети полного состояния одного такого компьютера понадобится 2n бит данных, в то время как для квантовой сети потребуется лишь n кубитов. Запутанность между всеми компьютерами в масштабах целой сети дает преимущество в скорости передачи информации на несколько порядков.

Итоги

Несмотря на квантовый мир, будоражащий множество умов по всему миру, квантовая запутанность сегодня является общепризнанным явлением, которое не только наблюдается экспериментально, но и используется в технологических процессах. Дальнейшее применение квантовой запутанности может вывести человечество на совсем иной уровень развития, с суперкомпьютерами и невообразимо быстрым интернетом.

Понравилась запись? Расскажи о ней друзьям!