Уравнение динамики прямолинейного движения автомобиля

Уравнение движения автомобиля выражает связь между движущими силами и силами сопротивления движению и позволяет определить режим движения автомобиля в любой момент.

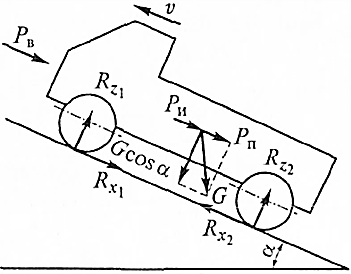
Для вывода уравнения движения используется схема движения автомобиля на подъем и рассматривается разгон автомобиля на подъеме (рис. 4.1).

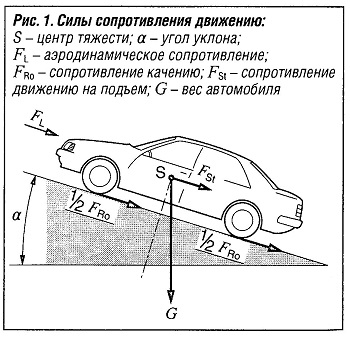
Рисунок 4.1 – Схема сил, действующих на автомобиль на подъеме

Проекция всех сил, действующие на автомобиль на поверхность дороги:

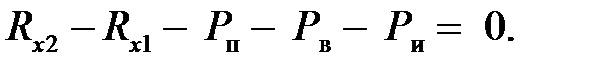(4.1)

Подставим в формулу (4.1) касательные реакции дороги R_х1 и R_х2, объединим члены с коэффициентом сопротивления качению f и члены с ускорением j и, принимая во внимание соотношения f (R_zl + R_z2) = P_к. При этом учтем, что j_k1 + j_k2 = j_k ,а также принимая во внимание коэффициент учета вращающихся масс, получим уравнение движения автомобиля в общем виде: .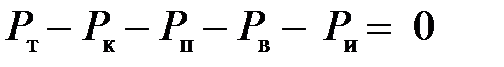

Принимая во внимание, что силы сопротивления качению Р_к и подъему Р_п в совокупности представляют силу сопротивления дороги Р_д, получим:

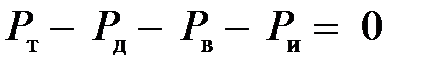(4.2)

При установившемся (равномерном) движении, когда нет разгона и Р_и = 0:

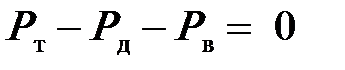(4.3)

Из уравнения (4.3) следует, что безостановочное движение автомобиля возможно только при условии:

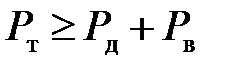(4.4)

Данное неравенство связывает конструктивные параметры автомобиля с эксплуатационными факторами, обусловливающими сопротивление движению, и не гарантирует отсутствия буксования ведущих колес. Безостановочное движение автомобиля без буксования ведущих колес возможно лишь при соблюдении условия:

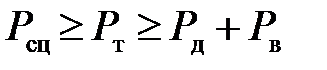(4.5)

Условие равномерного движения при отсутствии буксования ведущих колес записывается в виде:

Видео:Силы действующие на автомобиль при движении Подробный видеоурокСкачать

Устройство автомобилей

Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Уравнение движения автомобиля

Силовой баланс при прямолинейном движении автомобиля

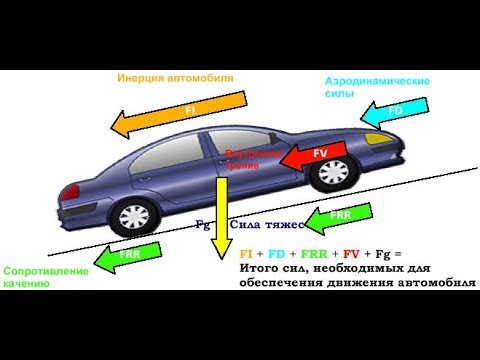
В предыдущей статье рассмотрены все силы, действующие на автомобиль во время его прямолинейного движения – сила тяги Р_т , сила тяжести G , сила сопротивления воздуха Р_ω , касательные R_x и нормальные R_y составляющие реакции дороги, силы инерции P_j , силы сопротивления подъему P_α , силы сопротивления качению колес P_f , и (в случае движения автопоезда) сила Р_пр на буксирном крюке.
Эти силы можно разделить на две группы – силы, обеспечивающие движение автомобиля, и силы сопротивления, препятствующие этому движению. В общем случае лишь одна сила обеспечивает его движение – сила тяги Р_т , приложенная к ведущим колесам. В частных случаях реально помогать движению автомобиля могут еще три силы – сила тяжести (при движении под уклон), сила инерции и сила попутного ветра. Тем не менее, эти силы при составлении динамического баланса тоже следует отнести к силам сопротивления движению автомобиля, учитывая лишь их векторное значение для каждого конкретного случая..

Спроектировав все силы на плоскость опорной поверхности автомобиля, получим уравнение динамики прямолинейного движения:

Очевидно, что движение возможно лишь в том случае, если сила тяги Р_т будет больше суммы сил P_ψ , P_j , P_ω , препятствующих движению. При этом движение возможно до тех пор, пока не начнется пробуксовка ведущих колес, т. е. сила тяги на ведущих колесах не превысит значение, при котором не будет иметь место сцепление шин с поверхностью дороги.

Сила тяги по сцеплению

Сила тяги образуется касательными реакциями дороги. Эти реакции представляют собой силы трения и силы зацепления, при этом силы зацепления возникают на деформируемых грунтах. Сила тяги ведущего колеса, которую можно реализовать для движения автомобиля на данном дорожном покрытии или грунте, имеет предел, зависящий от сцепных свойств шины.

Предельные значения силы тяги, которые можно реализовать по сцепным свойствам дороги, называют силой тяги по сцеплению P_φ . Основными факторами, влияющими на силу тяги по сцеплению, являются:

• нагрузка на ведущие колеса (сцепная нагрузка) и ее распределение по колесам;
• качество и состояние дорожного покрытия (грунта);
• удельное давление шин на дорогу;
• тип силовой передачи;
• состояние протектора шин.

Рассмотрим влияние каждого из этих факторов на силу тяги по сцеплению.

Сцепная нагрузка

При увеличении нагрузки на колесо увеличивается сила трения и сила зацепления. Сила тяги по сцеплению прямо пропорциональна сцепной нагрузке G_φ или нормальным реакциям на ведущих колесах:

где φ_x – коэффициент продольного сцепления колеса с опорной поверхностью.

А поскольку сила тяги определяется максимальным значением касательной реакции дороги, которая пропорциональна R_z , то можно записать:

где R_{x max} – максимально возможная продольная реакция по сцеплению.

Коэффициент φ_x определяется экспериментальным путем чаще всего при скольжении колеса в тормозном режиме, т. е. при протаскивании полностью заторможенного колеса:

Дорожное покрытие

Качество и состояние дорожного покрытия являются решающими факторами, влияющими на коэффициент сцепления φ_x . При движении автомобиля по дороге с твердым покрытием коэффициент продольного сцепления колеса с опорной поверхностью зависит от шероховатости и влажности дороги, наличия пыли и грязи. При этом даже тонкий слой воды на дорожном покрытии может не только существенно снизить φ_x , но и создавать подъемную силу, еще больше снижая сцепление шины с дорогой. Такой же и даже более выраженный эффект может создавать жидкая грязь на дороге.
Следует учитывать, что подъемная сила, возникающая при движении по мокрым и грязным дорогам, пропорциональная квадрату скорости движения автомобиля, и при большой скорости может вызвать аквапланирование, когда полностью прерывается контакт между шинами и дорогой.

Удельное давление на дорогу

Удельное давление шины на дорогу определяется площадью опорной поверхности шины и весом автомобиля, приходящимся на данное колесо. Регулировать удельное давление шины на дорогу можно изменением давления в шине – при снижении давления увеличивается площадь опорной поверхности и удельное давление снижается, и наоборот – при увеличении давления воздуха в шине уменьшается площадь опорной поверхности, что приводит к увеличению удельного давления колеса на дорогу.

Очевидно, что увеличение опорной поверхности шины с дорогой приводит к увеличению силы сцепления, особенно, на грунтовых дорогах, поскольку в зацеплении участвует большее количество грунтозацепов протектора покрышки.

При движении по влажным дорожным покрытиям повышенное удельное давление (давление в шинах) может благотворно сказаться на сцеплении шин с дорогой из-за выдавливания влаги из-под колес.

Удельное давление, оказываемое колесом на опорную поверхность, в некоторой степени зависит и от размеров шины – от ее диаметра и ширины. При увеличении диаметра колеса сегмент дуги, по которой осуществляется контакт шины с дорогой, имеет бȯльшую длину, чем опорный сегмент маленького колеса. Широкая шина создает колесу опору большей площади, чем узкая.

Влияние на сцепные свойства типа трансмиссии

Многочисленные опыты показали, что применение бесступенчатых трансмиссий обеспечивает повышение силы тяги по сцеплению. Главную роль здесь играет возможность плавного изменения величины тяговых моментов на ведущих колесах, без рывков и резких толчков.
В трансмиссиях, оснащенных ступенчатыми коробками передач, потеря сцепления колес с опорной поверхностью чаще всего имеет место во время переключения передач, сопровождающихся резким изменением величины крутящего момента на колесах.

Влияние конструкции шин

Важную роль в повышении сцепления колеса с дорогой играют рисунок протектора, а для шин повышенной проходимости размеры (особенно, высота) грунтозацепов протектора. Протектор шин легковых автомобилей обычной проходимости, как правило, имеет мелкий рисунок, обеспечивающий хорошее сцепление с твердым покрытием.
Наименьший коэффициент сцепления при прочих равных условиях у шин с изношенным рисунком протектора. Поэтому использование автомобилей с такими шинами запрещено.

Недостаточная величина коэффициента сцепления является причиной многих дорожно-транспортных происшествий. Для обеспечения безопасности дорожного движения его величина не должна быть меньше 0,4.

На дорогах с низкими сцепными свойствами коэффициент сцепления φx снижается до 0,2 и становится соизмеримым с коэффициентом сопротивления качению f . Это означает,что движение может оказаться невозможным из-за отсутствия запаса силы тяги по сцеплению. Следовательно, условие качения колес без скольжения можно представить в виде

Если сила тяги Р_т меньше силы сцепления Р_φ , ведущие колеса катятся без буксования. Если сила тяги превысит силу сцепления колес с дорогой, ведущие колеса будут пробуксовывать, а для движения использоваться лишь часть силы тяги, равная φR_z . Остальная часть силы тяги вызывает ускоренное вращение буксующих колес. Буксование колес связано со значительными потерями энергии на трение шин о дорогу и разрушение опорной поверхности.

Не менее вредное влияние на сцепную тягу автомобиля и его устойчивость на дороге оказывает скольжение заторможенных колес по твердому дорожному покрытию (блокировка колес). В этом случае изношенные частицы шины, попадая на опорную поверхность колеса и дороги, вызывают эффект «смазки», существенно снижая сцепные свойства шины. Это явление явилось причиной появления тормозных систем с антиблокировочными устройствами (АБС).

Условия возможности движения автомобиля

Согласно уравнению силового баланса (1) равномерное безостановочное движение автомобиля возможно лишь при условии

Выполнение этого условия для безостановочного движения автомобиля необходимо, но недостаточно, поскольку оно возможно лишь при отсутствии буксования ведущих колес.

Учитывая формулу (2) условие безостановочного движения можно выразить так:

Если суммарная сила сопротивления движению больше силы тяги, то двигатель автомобиля заглохнет. Если сила тяги превысит силу сцепления, ведущие колеса начнут пробуксовывать.

Формула (4) справедлива для полноприводных автомобилей, где вертикальная реакция R_z на ведущих колесах равна весу автомобиля. Для переднеприводных автомобилей вместо R_z следует подставить R_z1 , для заднеприводных – R_z2 .

Мощностной баланс автомобиля

Иногда вместо силового баланса, характеризуя возможность движения автомобиля, пользуются мощностным балансом. Мощность силы определяется ее модульной величиной и скоростью v движения тела под действием этой силы. Если умножить все члены уравнения силового баланса (1) на v /1000, получим уравнение мощностного баланса:

где N_т – тяговая мощность:

N_т = Р_тv/ 1000 = М_кi_трη_трv/ 1000 r = N_еη_тр
(здесь N_е – эффективная мощность двигателя, η_тр – КПД трансмиссии, i_тр – передаточное число трансмиссии);

N_α – мощность, затрачиваемая на преодоление подъема:

N_f – мощность, затрачиваемая на преодоление сопротивления качению:

N_ω — мощность, затрачиваемая на преодоление сопротивления воздуха:

N_j – мощность, затрачиваемая на преодоление сопротивления разгону:

N_ψ – мощность, затрачиваемая на преодоление сопротивления дороги:

Уравнение мощностного баланса устанавливает соотношения между мощностью, подводимой к ведущим колесам автомобиля и мощностью, необходимой для преодоления сопротивления движению автомобиля.

Используя уравнение мощностного баланса строят графики мощностного баланса для движения автомобиля на каждой из передач. Такие графики удобно использовать при сравнительной оценке тяговых свойств автомобиля графическими методами.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Автомобильный справочник

Видео:Физика - уравнения равноускоренного движенияСкачать

для настоящих любителей техники

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Динамика автомобиля

Под динамикой автомобиля понимают его свойство перевозить грузы и пассажиров с максимально возможной средней скоростью при заданных дорожных условиях. Чем лучше динамика автомобиля, тем выше его производительность. Кроме того, динамика автомобиля в полной мере определяет безопасность его эксплуатации. Динамика автомобиля зависит от его тяговых и тормозных свойств.

Видео:Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Динамика прямолинейного движения

Общее сопротивление движению

Сопротивление движению вычисляется как (рис. «Силы сопротивления движению» ):

Мощность, которая должна поступить на ве­дущие колеса автомобиля для преодоления сопротивления движению (силы сопротивле­ния движению), равна:

P_W = F_W v или P_W = F_WV /3600

Сопротивление качению

Сопротивление качению является следствием возникающих процес­сов деформации в зоне контакта шины с до­рогой. При этом применимо следующее:

Fro =f G cosa — fmg cosa

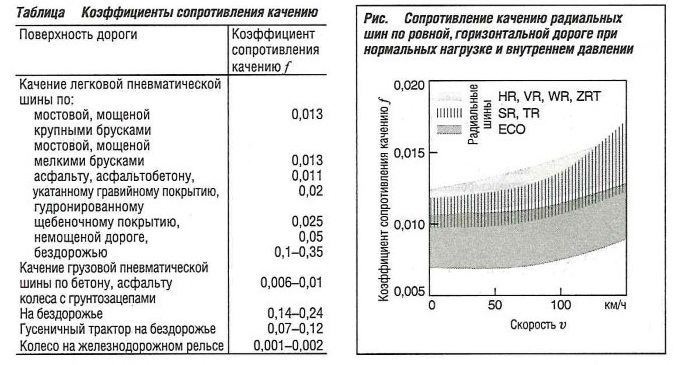
Приближенный расчет сопротивления каче­нию может быть выполнен путем использо­вания коэффициентов, представленных в приведенной ниже таблице «Коэффициенты сопротивления качению» и на рис. «Сопротивление качению радиальных шин по ровной, горизонтальной дороге при нормальных нагрузке и внутреннем давлении».

Увеличение коэффициента сопротивления качению f прямо пропорционально уровню деформации и обратно пропорционально ра­диусу шины. Следовательно, коэффициент будет увеличиваться при увеличении нагрузки, скорости и при снижении давления в шине.

При прохождении поворотов сопротивле­ние качению увеличивается за счет добавоч­ного сопротивления повороту:

F_k=f_кG

Коэффициент сопротивления повороту f_к является функцией скорости движения авто­мобиля, радиуса поворота, геометрических характеристик подвески автомобиля, типа шин, давления в шинах и поведения автомо­биля под действием поперечного ускорения.

Таблица.«Коэффициент аэродинамического сопротивления и мощность, затрачиваемая на преодоление аэродинамического сопротивления, для различных типов кузова»

Аэродинамическое сопротивление

Определяется по формуле:

F_L = 0,5 p⋅ c_w⋅ А (v + v₀) 2

F_L =0,0386⋅ р⋅ c_w⋅ А (v + v₀) 2 ,

где: v в км/ч, F_L в Н, р в кг/м 3 , А в м 2 , плотность воздуха р = 1,202 кг/м 3 на высоте 200 м.

P_L = F_L = 0,5 р c_w Av (v + v₀) 2

P_L = 12,9-10 -6 c_w A v (v + v₀) 2

Максимальное поперечное сечение автомобиля: А ≈0,9 х ширина колеи х высота.

Эмпирическое определение коэффициентов аэродинамического сопротивления и сопротивления качению

Автомобиль движется накатом на нейтральной передаче в условиях безветрия по ровной до­роге. Для двух заданных значений скоростей движения, v₁ (высокая скорость) и v₂ (малая скорость), замеряется время, необходимое, чтобы автомобиль при этих условиях замед­лил свое движение. Эта информация исполь­зуется для расчета средних замедлений a₁ и а₂. Формулы и примеры из табл. «Эмпирические определения коэффициентов аэродинамического сопротивления и сопротивления качению» приведены для автомобиля массой m = 1450 кг с площадью поперечного сечения А = 2,2 м 2 .

Этот метод применим для скоростей дви­жения автомобиля до 100 км/ч.

Сопротивление движению автомобиля на подъем и силы, действующие на автомобиль при движении под уклон

Сопротивление движению на подъем (F_st со знаком плюс) и силы, действующие на автомо­биль при движении под уклон (F_st со знаком минус) рассчитываются следующим образом:

F_st = G sinа = m g sina

F_st ≈ 0,01 m g p

Эти уравнения применимы с уклонами до р ⩽ 20%, поскольку при малых углах применимо следующее:

sina ≈ tana (погрешность менее 2 %).

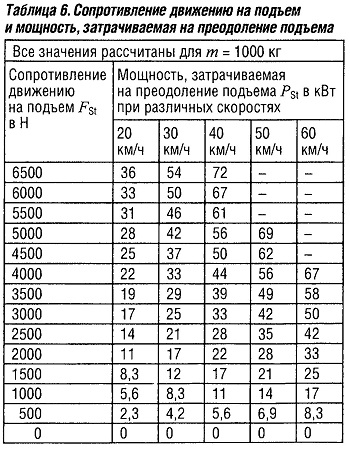
Мощность, затрачиваемая на преодоление подъема, равна:

P_st = F_st v или если P_st измеряется в кВт, F_st в Н и v в км/ч:

P_st = F_st v/3600 = m g v sina/3600

_Pst = m g p v / 3600

Продольный уклон дороги равен:

р = (h/l)⋅100 % или р = (tanа) ⋅100 %

где h соответствует проекции наклонной поверхности l на вертикальную ось.

В англоязычных странах продольный уклон определяется отношением 1 в 100/р .

Например, при р =50% отношение 1 к 2.

Пример вычисления силы тяги и мощности, затрачиваемой на преодоление подъема

Для преодоления подъема с уклоном р = 21 %, автомобилю массой 1500 кг потре­буется сила тяги на колесах приблизительно 1,5 x 2000 Н = 3000 Н (значение из табл. «Угол уклона и сопротивление движению на подъем» ) и при v = 40 км/ч мощность, затрачиваемая на преодоление подъема, приблизительно 1,5 х 22 кВт = 31 кВт (значение из табл. «Сопротивление движению на подъем и мощность, затрачиваемая на преодоление подъема» ).

Сила тяги

Чем больше крутящий момент двигателя М и общее передаточное число трансмиссии i между двигателем и ведущими колесами, и чем ниже потери мощности в трансмиссии, тем выше сила тяги F на ведущих колесах автомобиля.

F = (Mi/r)⋅η или F = P η / v

η — КПД привода. Для двигателя про­дольного расположения η ≈ 0,88 — 0,92, для двигателя поперечного расположения η ≈ 0,91 -0,95.

Сила тяги частично затрачивается на преодо­ление сопротивления движению. При боль­шом сопротивлении движению, имеющем место на подъемах, следует включать в ко­робке передач пониженную передачу (т. е. увеличивать передаточное число трансмис­сии).

Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Частота вращения коленчатого вала двигателя и скорость автомобиля

Частота вращения коленчатого вала вычисляется как:

n = 60vi / 2 πr

или при v в км/ч:

n = 1000vi / 2π·60r

Видео:МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать

Ускорение

Избыточная сила F-F_w вызывает ускорение автомобиля. Или замедление, когда Fw превышает F

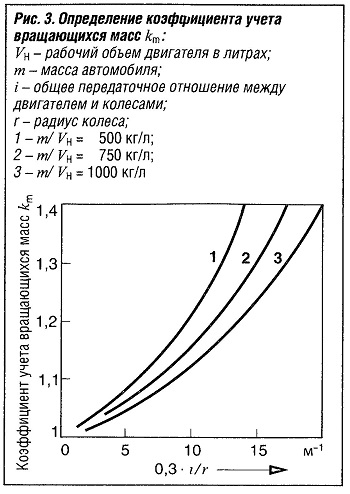
a = (F-Fw) / k_m m

a = (P η — P_w) / v k_m m

Коэффициент учета вращающихся масс k_m (рис. «Определение коэффициента учета вращающихся масс k_m» ) позволяет учесть дополнительное увеличение инерционных масс автомобиля из-за наличия вращающихся частей (колеса, маховик, коленчатый вал и т. п.).

Видео:Равномерное прямолинейное движение - физика 9Скачать

Сила тяги и скорость автомобилей с автоматической трансмиссией

Когда уравнение силы тяги применяется для автомобилей с автоматической трансмиссией с гидротрансформатором или гидромуфтой, крутящий момент двигателя заменяется крутящим моментом турбины гидротранс­форматора, а частота вращения коленча­того вала двигателя — частотой вращения турбины гидротрансформатора. Используя кривую характеристики гидротрансформа­тора, можно определить зависимость между

и скоростной характеристи­кой двигателя

Силовой баланс для отдельных передач в функции скорости движения может быть определена из диаграммы силы тяги/сопротивления движению. На диаграмме можно увидеть точки излома, типичные для гидротрансформатора, возникающие вслед­ствие мультипликации крутящего момента. Максимальную скорость в каждом случае для данной передачи можно определить по точкам пересечения линий тягового усилия с линиями сопротивления движению.

🎬 Видео

№ 2.16 Равноускоренное движение автомобиля│Задача по Динамике с нуляСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Прямолинейное движение. 10 класс.Скачать

Решение графических задач на равномерное движениеСкачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

1.4. Законы Ньютона как уравнение движения | Динамика | Александр Чирцов | ЛекториумСкачать

Физика. 10 класс. Основное уравнение динамики вращательного движенияСкачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать