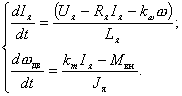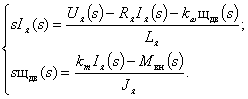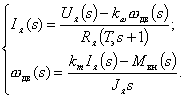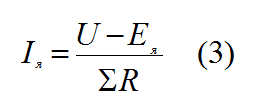Уравнение динамики двигателя постоянного тока

Важное свойство ДПТ с независимым возбуждением от постоянных магнитов состоит в том, что результирующий момент сил от всех проводников якоря, называемый электромагнитным моментом двигателя M, пропорционален току якоря I_я, потребляемому двигателем от источника питания:

,

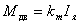
где k _m — коэффициент пропорциональности, называемый постоянной момента двигателя. Его размерность [Нм/А]. По законам электромагнитной индукции в проводнике, движущемся в магнитном поле, возникает электродвижущая сила. Суммарная ЭДС катушек якоря E через коллектор и щетки прикладывается к внешним выводам двигателя. В двигательном режиме работы эта ЭДС направлена против внешнего напряжения U _я, подведенного к якорю от источника питания. Поэтому ЭДС двигателя часто называется противоЭДС. Она прямо пропорциональна угловой скорости вращения вала двигателя w _дв[рад/с]:

,

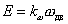
где k _ω — коэффициент пропорциональности, называемый постоянной ЭДС двигателя. Его размерность [Вс/рад].

Природа электромагнитных явлений в ДПТ такова, что если используется система единиц СИ, то значения коэффициентов k _ω и k_m численно равны.

Видео:Электродвигатель постоянного тока. Принцип работы.Скачать

Уравнения, описывающие электрические процессы в ДПТ

В электрической якорной цепи двигателя протекает ток I _я под действием напряжения постоянного тока U_a источника питания и противоЭДС двигателя.

Рис. 1

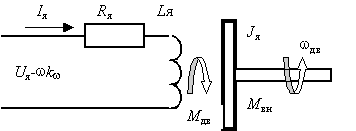
Эта цепь характеризуется параметрами: активным сопротивлением R _я [Ом] и индуктивностью L _я [Гн] якорной обмотки. Вращающийся ротор, обладающий моментом инерции J_a [Нм с 2 /рад] , приводится в движение одновременным действием электромагнитного момента двигателя M _дв и момента внешних сил M _вн, приложенного к валу двигателя.

Исходные дифференциальные уравнения ДПТ составляются на основании законов физики. Для электрической цепи используется второй закон Кирхгофа, согласно которому можно записать уравнение

,

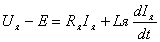
где член R _я I _я характеризует падение напряжения на активном сопротивлении якорной цепи в соответствии с законом Ома, а член L _я ( dI _я/ dt ) отражает наличие ЭДС самоиндукции, возникающей в обмотке при изменении тока якоря. В представленном уравнении не учитывается падение напряжения на щетках, зависящее нелинейно от тока якоря, но имеющее, как правило, относительно небольшое значение по сравнению с напряжением U _я .

Дифференциальное уравнение, характеризующее процессы в механической части двигателя, составляется на основании второго закона Ньютона:

,

где M _вн — момент внешних сил, действующий относительно оси вращения вала двигателя. В этом уравнении не учитывается действие сил трения, возникающих при вращении ротора, но оказывающих относительно слабое действие на ускорение вала ДПТ.

Используя вышеприведенные формулы и приводя дифференциальные уравнения к нормальной форме Коши, получим описание ДПТ в форме:

Для исследования процессов с помощью ЭВМ удобно использовать структурное представление математической модели ДПТ. Для этого преобразуем полученную систему линейных дифференциальных уравнений по Лапласу при нулевых начальных условиях. В результате получим систему алгебраических уравнений:

в которых s — переменная Лапласа, а величины I _я( s ), w _дв( s ), U _я( s ), M _вн( s ) — изображения по Лапласу переменных I _я , w _дв, U _я, M _вн соответственно. После эквивалентных преобразований эти уравнения могут быть представлены в форме:

где Т_э = L _я / R _я — электромагнитная постоянная времени якорной цепи двигателя.

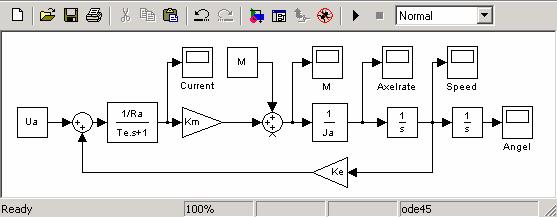
По уравнениям с помощью системы SIMULINK может быть сформирована структурная схема ДПТ для его математического моделирования (рис.1).

Важным параметром ДПТ, определяющим его динамические свойства, является электромеханическая постоянная времени двигателя:

.

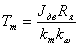
Зависимость между электромагнитным моментом двигателя и частотой вращения ротора в установившемся режиме при постоянных U _я и M _вн называется механической характеристикой двигателя. Уравнение механической характеристики имеет вид:

.

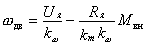
При пуске двигателя, когда скорость равна нулю, развивается пусковой момент

.

Частота вращения вала двигателя при отсутствии сопротивления называется частотой вращения холостого хода

.

Видео:Схема двигателя постоянного тока. Устройство и принцип работы.Скачать

Основные уравнения двигателя постоянного тока (ДПТ)

В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.

В результате взаимодействия I_я тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.

Видео:Как работает КОЛЛЕКТОРНЫЙ ЭЛЕКТРОДВИГАТЕЛЬ постоянного тока. Самое понятное объяснение! #shortsСкачать

Противо ЭДС двигателя E_я

При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС E_я направленная навстречу I_я. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.

C_e — постоянный коэффициент определяемой конструкцией двигателя.

Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.

где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :

• обмотки якоря
• добавочных полюсов
• обмотки возбуждения (для двигателей с последовательным возбуждением)

Видео:Управление двигателем постоянного тока. Схема управления мотором Ардуино проекты.Скачать

Ток якоря I_я

Выразим из формулы 2 ток якоря.

Видео:Принцип работы бесщеточного двигателя постоянного токаСкачать

Частота вращения якоря

Из формул 1 и 2 выведем формулу для частоты вращения якоря.

Видео:Электродвигатель постоянного токаСкачать

Электромагнитная мощность двигателя

Видео:Регулирование частоты вращения двигателей постоянного токаСкачать

Электромагнитный момент

где: ω = 2*π*f — угловая скорость вращения якоря, C_м — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)

Момент на валу двигателя, т.е. полезный момент, где М₀ момент холостого хода;

Видео:Электродвигатель постоянного тока с 3 катушками. Устройство и принцип работы.Скачать

Уравнение динамики двигателя постоянного тока

Принцип действия электрической машины постоянного тока может быть рассмотрен на примере простейшего генератора постоянного тока, функциональная схема которого показана на .

Рис. 5-1а. Простейшая машина постоянного тока.

Она представляет собой рамку, содержащую один или w витков, и вращающуюся с частотой ω в постоянном магнитном поле, создаваемом постоянным магнитом или электромагнитом.

По закону электромагнитной индукции при изменении потокосцепления в проводниках возникает ЭДС

где Ψ- потокосцепление, w — число витков, B — магнитная индукция, S — сечение, через которое проходит поток при взаимодействии с обмоткой. ЭДС возникает, если меняется во времени хотя бы одна из величин, стоящих в числителе формулы . В трансформаторах и машинах переменного тока изменяется магнитная индукция, а в машинах постоянного тока индукция постоянна, а изменяется площадь сцепления обмоток якоря с полем возбуждения из-за вращения ротора.

Если проводник перемещается в магнитном поле в плоскости, перпендикулярной силовым линиям, как это бывает в линейных двигателях, то

,

где l — длина проводника в поле, v — линейная скорость перемещения проводника.

Тогда согласно

При вращении с частотой ω

,

где D — диаметр ротора, как показано на .

Рис. 5-1б. ЭДС, возникающая при вращении якоря машины постоянного тока.

В этом случае согласно получим

т.е. в обмотке якоря индуцируется ЭДС, изменяющаяся по периодическому закону с частотой (см. ).

Рис. 5-1в. ЭДС, возникающая при вращении якоря машины постоянного тока.

Чтобы во внешней цепи ток протекал в одном направлении, он должен быть выпрямлен. Для этого служит специальный электромеханический выпрямитель — коллектор (К), расположенный на валу машины. В простейшем случае, как на , используются две пластины с наложенными на них щетками. Последние так должны быть расположены в пространстве, чтобы коммутация происходила в моменты периода ЭДС через ноль. При этом ЭДС, снимаемая со щеток, будет иметь вид, показанный на сплошной линией, пульсирующая ЭДС. С увеличением количества рамок (секций) и соответственно пластин коллектора пульсации уменьшаются. Так, на , пунктирной линией показана ЭДС при четырех коллекторных пластинах, а при восьми коллекторных пластинах пульсация напряжения на щетках не превышает 1% от среднего, поэтому ток, протекающий во внешней цепи, можно считать практически постоянным.

Рис. 5-1г. Возникающая ЭДС.

Магнитное поле, создаваемое в машине постоянного тока, состоит из двух составляющих — поля возбуждения, создаваемого постоянным магнитом или электромагнитом (см. ) и поля якоря (реакции) якоря, создаваемого током якоря, протекающим в обмотках якоря, расположенных на роторе (см. ).

Рис. 5-2а,б. Картина магнитного поля в машине постоянного тока.

Поле возбуждения неподвижно относительно статора, а поле реакции якоря из-за синхронной коммутации обмоток якоря вращается относительно ротора с той же частотой ω, с какой вращается сам ротор, но в обратную сторону, и таким образом также неподвижно относительно статора.

Направление потока реакции якоря совпадает с линией, на которой размещены щетки машины. При этом результирующая картина магнитного поля машины приобретает вид, представленный на .

Рис. 5-2в. Картина магнитного поля в машине постоянного тока.

Происходит искажение поля возбуждения и отклонения так называемой физической нейтрали от геометрической нейтрали на угол α. Чем больше нагружена машина, тем больше ток якоря, происходит большее искажение поля, натяжение магнитных силовых линий и увеличение угла α.

Таким образом, по принципу действия машина постоянного тока является обращенной синхронной машиной с синхронным коммутатором, в которой создается вращающееся магнитное поле не относительно статора, а относительно ротора, причем благодаря наличию коллектора (синхронного коммутатора) это поле вращается синхронно с ротором, но в обратную сторону, а при увеличении нагрузки происходит фазовый разворот этого поля относительно поля статора на угол α.

Весьма важен в машине постоянного тока процесс коммутации. При коммутации ток в коммутируемой секции обмотки якоря i_k меняет направление на обратное (см. ).

Рис. 5-3а,б,в. Коммутация секций обмотки якоря.

При отсутствии ЭДС в коммутируемой секции изменение тока i_k происходит по линейному закону — линия 1 на (линейная коммутация). Эквивалентная схема линейной коммутации показана на , где r_c — сопротивление секции, а r ₁ и r ₂ — сопротивления щеточных контактов, которые обратно пропорциональны площади щеточного контакта и меняются при повороте коллектора так, что токи i ₁ и i ₂ изменяются линейно за время коммутации, которое обычно составляет единицы миллисекунд.

В реальных условиях в короткозамкунотой секции существует ЭДС вращения, вызванная реакцией якоря, и ЭДС самоиндукции, которые приводят к задержке спада тока i_k — замедленная коммутация (кривая 2 на ).

Это приводит к усилению искрения на сбегающем крае щеточного контакта, которое может оказаться опасным для машины. Для улучшения условий коммутации в больших машинах создаются дополнительные полюса, компенсирующая ЭДС самоиндукции и компенсационные обмотки, нейтрализующие реакцию якоря. В нереверсивных машинах малой мощности производится смещение щеток на физическую нейтраль.

Чрезмерно большой поток добавочных полюсов также нежелателен. При прекомпенсации возникает так называемая ускоренная коммутация, (кривая 3 на ), при которой появляется искрение под набегающим краем щетки.

Рассмотрим электромеханическое преобразование энергии в машине постоянного тока на примере двигателя с возбуждением от постоянного магнита, схема которого приведена на .

Рис. 5-4а. Двигатель постоянного тока.

Эквивалентная схема якорной цепи показана на , где R _Я — активное сопротивление обмоток якоря, L _Я — индуктивность обмоток, E _Я — среднее значение ЭДС вращения.

Рис. 5-4б. Эквивалентная схема двигателя постоянного тока.

При достаточно большом количестве секций обмоток якоря и соответствующем ему количестве пластин коллектора ЭДС вращения E _Я практически не имеет пульсаций и не зависит от положения ротора, а только от скорости его вращения. Поэтому ее можно вычислять не по , а по , приняв ; , где N — общее число проводников якоря, 2· a — число параллельных ветвей обмотки, D — диаметр якоря.

Магнитную индукцию B можно выразить через поток возбуждения Ф_В:

,

где S — площадь полюсного наконечника.

,

где p — число пар полюсов машины.

Подставляя все эти выражения в формулу , получим

т.е. ЭДС вращения зависит от конструктивных параметров, потока возбуждения и частоты вращения. Обозначив совокупность конструктивных параметров в через коэффициент K _ЭМ , получим выражение для ЭДС вращения в следующем виде:

При неизменном потоке возбуждения, как это принято в данном случае при возбуждении от постоянного магнита, вводят понятие электромагнитного коэффициента

,

который может быть определен по номинальным данным электрической машины. Тогда формула будет иметь вид:

Пользуясь эквивалентной схемой , можно построить энергетическую диаграмму двигателя. В установившемся режиме для эквивалентной схемы имеем электрические уравнения

где P ₁ = U · I _Я — мощность потребляемая из сети, P _ЭП = I _Я 2 · R _Я — электрические потери в обмотке якоря, P _ЭМ = E _Я · I _Я — электромагнитная мощность, содержащаяся в магнитном поле.

Электромагнитную мощность, исходя из закона сохранения энергии, можно представить через электромагнитный момент M :

.

Откуда, учитывая выражения

Согласно диаграмме на мощность, поступающая на вал P ₂ , будет меньше электромагнитной мощности на величину потерь в стали P_MAT и механических потерь P_MEX . Вращающий момент (момент на валу) будет соответственно меньше электромагнитного момента

Рис. 5-4в. Энергетическая диаграмма двигателя постоянного тока.

из-за этих потерь, так как

,

.

5.2. Двигатели постоянного тока

Двигатели постоянного тока различаются по характеру возбуждения. Двигатели могут быть независимого, параллельного, последовательного и смешанного возбуждения (см. ). Свойства двигателей в значительной мере определяются их системой возбуждения.

Рис. 5-5а,б,в,г. Возбуждение ДПТ.

Поскольку в автоматике применяются в основном двигатели независимого возбуждения, будем в дальнейшем рассматривать двигатели этого типа ( ).

Различают статические и динамические режимы работы двигателей. В статическом режиме ω= const ; I _Я = const ; U _ДВ = const и он описывается так называемыми механическими характеристиками

.

В статическом режиме двигатель независимого возбуждения описывается следующей системой уравнений:

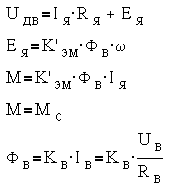
где первое уравнение — уравнение якорной цепи, второе и третье — и , четвертое — механическое уравнение, пятое — уравнение цепи возбуждения.

Из первых четырех уравнений получим уравнение механической характеристики:

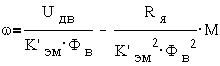
Поскольку применяемые в системах автоматического управления двигатели являются управляемыми, различают два типа управления двигателями постоянного тока — якорное управление и полюсное управление.

При якорном управлении производится изменение напряжения, подаваемого в якорную цепь без изменения возбуждения. При полюсном управлении, наоборот, меняется поле возбуждения путем изменения тока в обмотках главных полюсов i_B . Для расширения диапазона управления применяют также комбинированное управление.

При полюсном управлении Ф _B = const , поэтому уравнение механической характеристики согласно будет иметь вид:

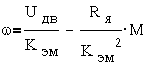
Графически эта характеристика при фиксированном напряжении на двигателе представляет собой прямую, пересекающую координатные оси в точках ω₀ и M _К.З. (см. ), где ω₀— частота вращения холостого хода, а M _К.З. — момент короткого замыкания, когда ротор двигателя неподвижен.

Рис. 5-6а. Статическая характеристика ДПТ.

Электрическая машина работает в режиме двигателя при 0 M M _К.З. , при M > M _К.З. происходит вращение двигателя в противоположную сторону под действием внешнего момента — машина работает в режиме тормоза (режим противовключения), при ω>ω₀ машина работает в режиме генератора на сеть, имеющую напряжение U_H .

Рис. 5-6б. Статическая характеристика ДПТ.

Механические характеристики при различных напряжениях питания двигателя выглядят, как семейство прямых, показанных на . Часто их строят в функции тока якоря I _Я , тогда аналитическое выражение для механических характеристик примет вид:

откуда видно, что падение скорости при нагрузке двигателя зависит исключительно от сопротивления якорной цепи R _Я .

Кроме механических, существуют регулировочные характеристики. Для якорного управления это зависимость частоты вращения от напряжения питания U _ДВ . Вид этих характеристик показан на , где U _ТР — напряжение трогания двигателя.

Регулировочная характеристика для полюсного управления может быть получена из при U _ДВ = const .

Рис. 5-6в. Статическая характеристика ДПТ.

Вид этих характеристик при различных нагрузках показан на .

Рис. 5-6г. Статическая характеристика ДПТ.

Для холостого хода, когда M =0, эта характеристика имеет вид гиперболы

Двигатель постоянного тока как динамическая система описывается следующими уравнениями в операторной форме:

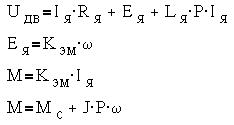
На основании этих уравнений может быть построена структурная схема двигателя как динамической системы ( ).

Рис. 5-7а. Структурная схема ДПТ.

Из структурной схему получим передаточные функции двигателя:

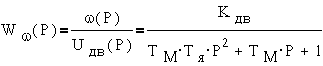
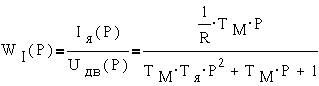
где — коэффициент передачи, — постоянная времени якоря, — электромеханическая постоянная времени.

Пользуясь формулой Хевисайда, по передаточным функциям можно построить переходные процессы, например при пуске двигателя, как это показано на .

Рис. 5-7б. Переходный процесс при пуске ДПТ.

При T_M » T _Я , как это обычно бывает, получим выражения для тока и скорости при пуске:

Для анализа динамики двигателя постоянного тока при полюсном управлении рассматривают уравнения, аналогичные уравнениям в отклонениях, так как регулировочная характеристика при полюсном управлении является нелинейной.

Производят линеаризацию системы для малых отклонений относительно каких-то нулевых значений, представив переменные в следующем виде:

; ; ; ;

Тогда на основании уравнений можно написать уравнения в отклонениях (при T _Я =0).

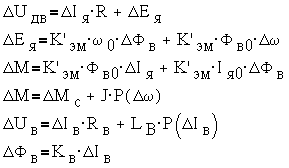
На основании этих уравнений может быть построена структурная схема двигателя как динамической системы при полюсном управлении ( ).

Рис. 5-8а. Структурная схема ДПТ при полюсном управлении.

С помощью этой схемы получим передаточную функцию для ДПТ при полюсном управлении

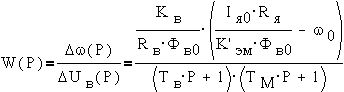
По этой передаточной функции, пользуясь формулой Хевисайда, можно получить кривые переходного процесса в двигателе при ступенчатом изменении напряжения возбуждения, показанные на .

Рис. 5-8б. Переходный процесс при пуске ДПТ при полюсном управлении.

5.3. Генераторы постоянного тока

Генераторы постоянного тока, также как и двигатели, различают по характеру их возбуждения. В зависимости от этого их подразделяют на генераторы независимого возбуждения и самовозбуждением. В генераторах независимого возбуждения поток возбуждения может создаваться обмоткой возбуждения (электромагнитное возбуждение) или с помощью постоянного магнита (магнитоэлектрическое возбуждение). Генераторы с самовозбуждением бывают параллельного и смешанного возбуждения(см. ).

Рис. 5-9а. Схема генератора постоянного тока.

О свойствах генератора судят по его основным характеристикам, к которым относят характеристику холостого хода, а также нагрузочную, внешнюю и регулировочную.

Под характеристикой холостого хода понимают зависимость U = f ( I_B ) при I _Я =0 и ω= const (кривая 1 на ). Эта зависимость характеризует свойства магнитной цепи машины, и по ней можно определить условие самовозбуждения генератора с параллельным возбуждением, это возможно, если сопротивление обмоток возбуждения меньше критического R _ВХ . При выполнении этого условия установившееся значение напряжения на выходе генератора будет соответствовать точке пересечения характеристики холостого хода и прямой I_B · R_B (см. ).

Рис. 5-9б. Статическая характеристика генератора постоянного тока.

Внешняя характеристика ( ) представляет собой зависимость U = f ( I _Я ) при ω = const .

Рис. 5-9в. Статическая характеристика генератора постоянного тока.

Кривая 1 соответствует генератору с независимым возбуждением при I_B = const .С увеличением тока якоря (нагрузки) напряжение на зажимах генератора уменьшается из-за падения напряжения на сопротивлении якоря R _Я и реакции якоря. В генераторе с параллельным возбуждением это уменьшение происходит более интенсивно (кривая 2), так как оно усугубляется уменьшением тока возбуждения. Для компенсации уменьшения напряжения при увеличении нагрузки применяется комбинированное возбуждение (кривая 3).

Нагрузочная характеристика — это зависимость U = f ( I_B ) при I _Я = const (кривая 2 на ). Она проходит ниже характеристики холостого хода 1 вследствие падения напряжения в якорной цепи и реакции якоря. Чем больше ток якоря, тем ниже характеристика 2 проходит по отношению к характеристике 1.

Регулировочная характеристика — это зависимость I_B = f ( I _Я ) при U = const ( ). Чтобы поддержать напряжение постоянным, необходимо при увеличении тока I _Я увеличивать ток возбуждения.

Рис. 5-9г. Статическая характеристика генератора постоянного тока.

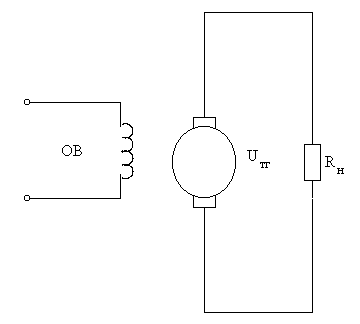
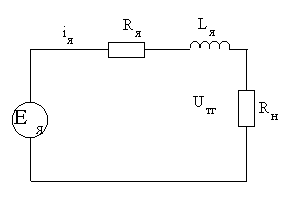
В системах автоматического управления широкое применение имеют тахогенераторы постоянного тока. Тахогенераторы представляют собой генераторы небольшой мощности, служащие для преобразования частоты вращения в электрический сигнал. Как правило, тахогенераторы выполняют с независимым электромагнитным или магнитоэлектрическим возбуждением ( ).

Рис. 5-10а,б. Схема тахогенератора.

Выходная характеристика тахогенератора — это зависимость U _ТГ = f (ω). Она может быть получена из анализа эквивалентной схемы якорной цепи, представленной на . Откуда в установившемся режиме получим:

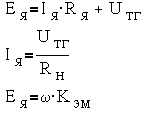
Из этих уравнений получим выражение для выходной характеристики:

где K _ТГ — коэффициент передачи тахогенератора, который определяет крутизну выходной характеристики тахогенератора (см. ). Чем больше К_ЭМ=К`_ЭМ·Ф _B и больше R_H по сравнению с R _Я тем больше крутизна характеристики.

Рис. 5-10в. Характеристики тахогенератора.

Из следует, что выходное напряжение U _ТГ и при нагрузке является линейной функцией частоты вращения. Однако практически выходная характеристика отклоняется от линейной ( ) из-за реакции якоря, ослабляющей поток возбуждения Ф_В. Отклонение от линейности определяет одну из основных погрешностей тахогенератора. Для уменьшения ее следует нагружать тахогенератор на относительно большое сопротивление нагрузки R_H и использовать небольшой диапазон частот вращения.

Тахогенератор как динамическая система описывается уравнениями, аналогичными уравнениям :

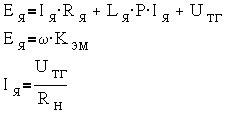
Откуда может быть получена передаточная функция тахогенератора

где — постоянная времени тахогенератора.

5.4. Вентильные двигатели

Машины постоянного тока имеют более высокие технические показатели (линейность характеристики, высокий КПД, малые габариты), чем машины переменного тока. Существенный недостаток — наличие электромеханического коллектора, который снижает надежность, создает радиопомехи, взрывоопасность и т.д.

Этих недостатков лишен бесконтактный двигатель постоянного тока, называемый вентильным двигателем. В этом двигателе щеточный аппарат заменен полупроводниковым коммутатором, якорь находится на статоре, а ротор представляет собой двухполюсный (реже четырехполюсный) постоянный магнит. Для упрощения коммутатора число секции обмотки якоря выбирается малым — три, четыре.

Рис. 5-11а. Трехфазный вентильный двигатель.

Схема трехфазного вентильного двигателя с двухполюсным ротором представлена на . Существенным элементом двигателя является датчик положения — ДПР. Он может основан на разных принципах — фотоэлектрические, индуктивные, емкостные, на эффекте Холла, и т.д. В рассматриваемом двигателе применяется фотоэлектрический датчик, содержащий три неподвижных фотоприемника mlk , которые закрываются поочередно вращающейся шторкой. Двоичный код, получаемый с ДПР, фиксирует шесть различных положений ротора (шесть фаз), это соответствие кодов и фаз приведено в верхней части .

В этой таблице единице соответствует наличие сигнала на выходе датчика, т.е. когда фотоприемник открыт, а нулю — отсутствие сигнала, когда соответствующий фотоэлемент закрыт шторкой.

Рис. 5-11б. Трехфазный вентильный двигатель.

Сигналы датчиков преобразуются управляющим устройством УУ ( ) в комбинацию управляющих напряжений U ₁ — U ₆ , которые управляют транзисторными ключами K ₁ — K ₆ согласно нижней части , так, что в каждый такт (фазу) работы двигателя включены два ключа — верхний и нижний и к сети подключены последовательно две из трех обмоток якоря. Обмотки якоря a , b , c расположены на статоре со сдвигом на 120·град (см. ) и их начала и концы соединены так, что при переключении ключей создается вращающееся магнитное поле. Одному циклу работы коммутатора соответствует один оборот ротора. Цикл делится на шесть тактов (временных фаз), которым соответствует пространственный угол α=60·град. Коммутация производится так, что поток возбуждения Ф₀ отстает на угол α от потока якоря. На токи в обмотках и положение ротора показаны для фазы 1. В результате взаимодействия потока якоря и возбуждения создается вращающий момент M , который стремится развернуть ротор так, чтобы потоки якоря и возбуждения совпали, но при повороте ротора под действием ДПР происходит переключение обмоток и поток якоря поворачивается на следующий шаг.

Рис. 5-12б. Временная диаграмма трехфазного вентильного двигателя.

Временная диаграмма работы вентильного двигателя приведена на . Как видно из диаграммы, вентильный двигатель работает как в данном случае трехфазный синхронный двигатель, частота вращения его ротора пропорциональна частоте вращения поля. Основным отличием от синхронного является его самосинхронизация с помощью ДПР, в результате чего у этого двигателя, наоборот, частота вращения поля пропорциональна (в данном случае при двухполюсном якоре равна) частоте вращения ротора, а частота вращения ротора зависит от напряжения питания, т.е. двигатель работает как двигатель постоянного тока.

В отличие от двигателя постоянного тока, так как вентильный двигатель имеет мало секций в обмотке якоря, момент имеет пульсации, и среднее значение момента зависит от периода включения ключа β, показанного на .

В получена формула для среднего значения электромагнитного момента вентильного двигателя

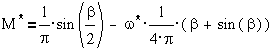
где M * и ω * — относительные момент и частота вращения по отношению к базовым:

; ; ; ,

где m — число обмоток (секций), R — сопротивление секции.

Учитывая эти соотношения, из 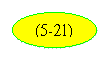можно получить выражение для механической характеристики вентильного двигателя

где A и B — коэффициенты, зависящие от β.

;

Эти коэффициенты зависят от способа коммутации обмоток и приведены в .

🎬 Видео

Электродвигатели постоянного токаСкачать

Обзор двигателей постоянного тока ДПМ , ДПР , ДП.Скачать

Тормозные режимы двигателей постоянного токаСкачать

Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Динамика строительства AO FAZOTRON за январь 2024 годаСкачать

Модель двигателя постоянного токаСкачать

Способы регулирования частоты вращения якоря машины постоянного токаСкачать

Как Работает Электрический Двигатель Постоянного ТокаСкачать

Характиристики машин постоянного токаСкачать

Коллекторные двигатели.Скачать

Общее уравнение динамикиСкачать

Двигатель постоянного тока как преддверие к сверх единице. Социальный пapaзитизмСкачать