Уравнение диагонали квадрата по координатам

Видео:№931. Начертите квадрат MNPQ так, чтобы вершина Р имела координаты (-3; 3), а диагонали квадратаСкачать

Задача 31272 Известна точка пересечения диагоналей.

Условие

Известна точка пересечения диагоналей квадрата К( 1,5; 2,5) и уравнение одной из его сторон х-4у = 0. Найти координаты вершин квадрата и составить уравнения его диагоналей.

Все решения

Уравнение стороны запишем в виде
y=(1/4)x
k=1/4
tg α =1/4

Уравнение диагонали в общем виде:
y=k_(1)x+b

(Диагонали квадрата являются биссектрисами прямых углов квадрата, значит угол между стороной и диагональю квадрата равен 45^(o))

Так как
tg( β — α )=(tg β -tg α )/(1+tg β *tg α )
и

y=(5/3)x+b — уравнение диагонали

Подставим координаты точки К

Диагонали взаимно перпендикулярны.
Значит уравнение второй диагонали
y=(-3/5)x+b
Подставим координаты точки К
2,5=(-3/5)*1,5+b
b=3,4

Координаты одной вершины получим как координаты точки пересечения стороны х-4у=0 и диагонали у=(5/3)х
<х-4у=0
<у=(5/3)х

Координаты второй вершины получим как координаты точки пересечения стороны х-4у+24=0 и диагонали у=(-3/5)х+3,4
<х-4у=0 ⇒ y=(1/4)x
<у=(-3/5)х+3,4

Координаты двух других точек можно найти из симметрии.

Видео:Площадь квадрата через диагональ 📐 Полезный файлик в комментариях)Скачать

Уравнение квадрата в декартовой системе координат.

Проанализируем расположение квадрата на координатной плоскости.

В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:

где точка О`(a;b) – точка пересечения диагоналей квадрата;

d – длина диагонали квадрата.

В частном случае, когда точка О(0;0) — начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:

где d– длина диагонали квадрата.

Видео:7 Точки с целыми координатами и диагональ квадратаСкачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:Метод координат для ЕГЭ с нуля за 30 минут.Скачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Уравнения стороны треугольника и медианыСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:Быстрый способ решения квадратного уравненияСкачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:9 класс, 4 урок, Простейшие задачи в координатахСкачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

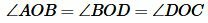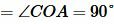(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

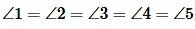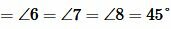(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

🔥 Видео

Задача, которую боятсяСкачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

№579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координатыСкачать

УРАВНЕНИЕ ПРЯМОЙСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать