Уравнение де бройля для свободно движущейся частицы в параметрах (2 видео)

Содержание

Уравнение де бройля для свободно движущейся частицы в параметрах
Волны де Бройля de Broglie waves
Уравнение де бройля для свободно движущейся частицы в параметрах
5.1.5 Волновые свойства частиц. Волны де Бройля. Длина волны де Бройля движущейся частицы
🎥 Видео

Видео:Волна де Бройля (видео 4) | Квантовая физика | ФизикаСкачать

Уравнение де бройля для свободно движущейся частицы в параметрах

Волны де Бройля
_{de Broglie waves}

Волны де Бройля – волны, связанные с любой движущейся материальной частицей. Любая движущаяся частица (например, электрон) ведёт себя не только как локализованный в пространстве перемещающийся объект — корпускула, но и как волна, причём длина этой волны даётся формулой λ = h/р, где h = 6.6·10 -34 Дж . сек – постоянная Планка, а р – импульс частицы. Эта волна и получила название волны де Бройля (в честь французского физика-теоретика Луи де Бройля, впервые высказавшего гипотезу о таких волнах в 1923 г.). Если частица имеет массу m и скорость v 2 − энергия покоя частицы массы m,
λ_{комптон} = h/mc − комптоновская длина волны частицы,
λ_{комптон} (электрон) = 2.4·10 -12 м = 0.024 Å,
λ_{комптон} (протон) = 1.32·10 -15 м = 1.32 фм.
Длина волны де Бройля фотона с энергией Е определяется из соотношения

λ(фм) = h/p = hc/E = 2π·197 МэВ·фм /E(МэВ).

Существование волн де Бройля доказано многочисленными экспериментами, в которых частицы ведут себя как волны. Так при рассеянии пучка электронов с энергией 100 эВ на упорядоченной системе атомов кристалла, играющего роль дифракционной решётки, наблюдается отчётливая дифракционная картина. Существование волн де Бройля лежит в основе работы электронного микроскопа, разрешающая способность которого намного порядков выше, чем у любого оптического микроскопа, что позволяет наблюдать молекулы и атомы, а также в основе методов исследования таких сверхмалых объектов, как атомные ядра и элементарные частицы, бомбардировкой их частицами высоких энергий. Метод дифракции частиц в настоящее время широко используется при изучении строения и свойств вещества.

Видео:Волновые свойства частиц. Волны де Бройля. 11 класс.Скачать

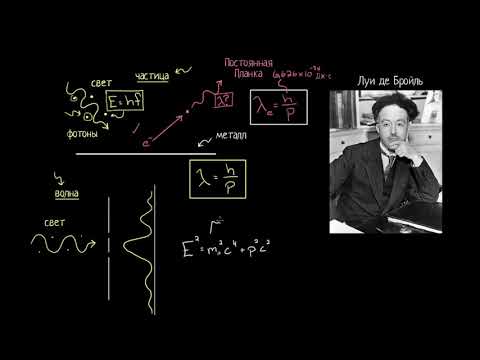
Уравнение де бройля для свободно движущейся частицы в параметрах

Элементы квантовой механики

Корпускулярно-волновой дуализм свойств частиц вещества.

§1 Волны де Бройля

В 1924г. Луи де Бройль (французский физик) пришел к выводу, что двойственность света должна быть распространена и на частицы вещества — электроны. Гипотеза де Бройля заключалась в том, что электрон, корпускулярные свойства которого (заряд, масса) изучаются давно, имеет еще и волновые свойства, т.е. при определенных условиях ведет себя как волна.

Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов.

Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

— волна де Бройля

p = mv — импульс частицы, h — постоянная Планка.

Волны де Бройля , которые иногда называют электронными волнами, не являются электромагнитными.

В 1927 году Дэвиссон и Джермер ( амер. физик ) подтвердили гипотезу де Бройля обнаружив дифракцию электронов на кристалле никеля. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов 2 dsin j = n l , а брэгговская длина волны оказалась в точности равной .

Дальнейшее подтверждение гипотезы де Бройля в опытах Л.С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (Е » 50 кэВ) через фольгу из различных металлов. Затем была обнаружена дифракция нейтронов, протонов, атомных пучков и молекулярных пучков. Появились новые методы исследования вещества — нейтронография и электронография и возникла электронная оптика.

Макротела также должны обладать всеми свойствами ( m = 1кг, следовательно, l = 6 . 6 2 · 1 0 — 3 1 м — невозможно обнаружить современными методами — поэтому макротела рассматриваются только как корпускулы).

§2 Свойства волн де Бройля

Пусть частица массы m движется со скоростью v . Тогда фазовая скорость волн де Бройля

Т.к. c > v , то фазовая скорость волн де Бройля больше скорости света в вакууме ( v _ф может быть больше и может быть менше с, в отличие от групповой ).

следовательно, групповая скорость волн де Бройля равна скорости движения частицы.

т.е. групповая скорость равная скорости света.

Волны де Бройля испытывают дисперсию. Подставив в получим, что v_ф = f (λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10 -26 с.

§3 Соотношение неопределенностей Гейзенберга

Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р. Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.

Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к. . Только рассматривая протяженный участок D C мы сможем определить импульс частицы. Чем больше D C , тем точнее D р и наоборот, чем меньше D C , тем больше неопределенность в нахождении D р .

Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точности канонически сопряженных величин, к которым относятся координата и импульс, энергия и время.

Соотношение неопределенностей Гейзенберга: произведение неопределенностей значений двух сопряженных величин не может быть по порядку величины меньше постоянной Планка h

( иногда записывают )

Таким образом. для микрочастицы не существует состояний, в которых её координата и импульс имели бы одновременно точные значения. Чем меньше неопределенность одной величины, тем больше неопределенность другой.

Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

следовательно, чем больше m , тем меньше неопределенности в определении координаты и скорости. При m = 10 -12 кг , ? = 10 -6 и Δ x = 1% ?, Δv = 6,62·10 -14 м/с, т.е. не будет сказываться при всех скоростях, с которыми пылинки могут двигаться, т.е. для макротел их волновые свойства не играют никакой роли.

Пусть электрон движется в атоме водорода. Допустим Δ x » 1 0 -10 м (порядка размеров атома, т.е. электрон принадлежит данному атому). Тогда

Δv = 7,27· 1 0 6 м/с. По классической механике при движении по радиусу r » 0 , 5 · 1 0 — 1 0 м v = 2,3·10 -6 м/с. Т.е. неопределенность скорости на порядок больше величины скорости, следовательно, нельзя применять законы классической механики к микромиру.

Из соотношения следует, что система имеющая время жизни D t , не может быть охарактеризована определенным значением энергии. Разброс энергии возрастает с уменьшением среднего времени жизни. Следовательно, частота излученного фотона также должна иметь неопределенность D n = D E / h , т.е. спектральные линии будут иметь некоторую ширину n ± D E / h , будут размыты. Измерив ширину спектральной линии можно оценить порядок времени существования атома в возбужденном состоянии.

§4 Волновая функция и ее физический смысл

Дифракционная картина, наблюдающаяся для микрочастиц, характеризуется неодинаковым распределением потоков микрочастиц в различных направлениях — имеются минимумы и максимумы в других направлениях. Наличие максимумов в дифракционной картине означает, что в этих направлениях распределяются волны де Бройля с наибольшей интенсивностью. А интенсивность будет максимальной, если в этом направлении распространяется максимальное число частиц. Т.е. дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности в распределении частиц: где интенсивность волны де Бройля максимальная, там и частиц больше.

Волны де Бройля в квантовой механике рассматриваются как волны вероятности, т.е. вероятность обнаружить частицу в различных точках пространства меняется по волновому закону ( т.е.

е — iωt ). Но для некоторых точек пространства такая вероятность будет отрицательной (т.е. частица не попадает в эту область). М. Борн ( немецкий физик ) предположил, что по волновому закону меняется не сама вероятность, а амплитуда вероятности, которую также называют волновой функцией или y -функцией (пси — функцией).

Волновая функция — функция координат и времени.

Квадрат модуля пси-функции определяет вероятность того, что частица будет обнаружена в пределах объема dV — физический смысл имеет не сама пси-функция, а квадрат ее модуля.

Ψ * — функция комплексно сопряженная с Ψ

Если частица находится в конечном объеме V , то возможность обнаружить ее в этом объеме равна 1, (достоверное событие)

Р = 1 Þ

В квантовой механике принимается, что Ψ и АΨ, где А = const , описывают одно и то же состояние частицы. Следовательно,

интеграл по , означает, что он вычисляется по безграничному объему (пронстранству).

y — функция должна быть

1) конечной (так как Р не может быть больше1),

2) однозначной (нельзя обнаружить частицу при неизменных условиях с вероятностью допустим 0,01 и 0,9, так как вероятность должна быть однозначной).

непрерывной (следует из неприрывности пространства. Всегда имеется вероятность обнаружить частицу в разных точках пространства, но для разных точек она будет разная),
Волновая функция удовлетворяет принципусуперпозиции: если система может находится в различных состояниях, описываемых волновыми функциями y ₁ , y ₂ . y _n , то она может находится в состоянии y , описываемой линейной комбинаций этих функций:

С _n ( n =1,2. ) — любые числа.

С помощью волновой функции вычисляются средние значения любой физической величины частицы

§5 Уравнение Шредингера

Уравнение Шредингера, как и другие основные уравнения физики (уравнения Ньютона, Максвелла), не выводится, а постулируется. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия точно согласуются с экспериментальными данными.

(1)

— Временное уравнение Шредингера.

— набла — оператор Лапласа

— потенциальная функция частицы в силовом поле,

Ψ( y , z , t ) — искомая функция

Если силовое поле, в котором движется частица, стационарно (т.е. не изменяется с течением времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера (т.е. Ψ — функция) может быть представлено в виде произведения двух сомножителей — один зависит только от координат, другой — только от времени:

(2)

Е — полная энергия частицы, постоянная в случае стационарного поля.

(3)

— Уравнение Шредингера для стационарных состояний.

Имеется бесконечно много решений. Посредством наложения граничных условий отбирают решения, имеющие физический смысл.

волновые функции должны быть регулярными, т.е.

Решения, удовлетворяющие уравнению Шредингера, называются собственными функциями, а соответствующие им значения энергии — собственными значениями энергии. Совокупность собственных значений называется спектром величины. Если Е _n принимает дискретные значения, то спектр — дискретный, если непрерывные — сплошной или непрерывный.

§6 Движение свободной частицы

Частица называется свободной, если на нее не действуют силовые поля, т.е. U = 0.

Уравнение Шредингера для стационарных состояний в этом случае:

И собственные значения энергии:

Т.к. k может принимать любые значения, то, следовательно, и Е принимает любые значения, т.е. энергетический спектр будет сплошным.

Временная волновая функция

(- уравнение волны)

т.е. представляет плоскую монохромную волну де Бройля.

§7 Частица в “потенциальной яме” прямоугольной формы.

Квантование энергии.

Найдем собственные значения энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Предположим что, частица может двигаться только вдоль оси x . Пусть движение ограничено непроницаемыми для частицы стенками x = 0, и x = ?. Потенциальная энергия U имеет вид:

Уравнение Шредингера для стационарных состояний для одномерной задачи

За пределы потенциальной ямы частица попасть не сможет, поэтому вероятность обнаружения частицы вне ямы равна 0.Следовательно, и Ψ за пределами ямы равна 0 .Из условий непрерывности следует, что Ψ = 0 и на границах ямы т.е.

В пределах ямы (0 £ x £ l ) U = 0 и уравнение Шредингера.

введя получим

;

из граничных условий следует

Из граничного условия

Энергия Е _n частицы в «потенциальной яме» с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е _n называются уровнями энергии, а число n , определяющее энергические уровни частицы, называется главным квантовым числом. Т.е. частицы в «потенциальной яме» могут находиться только на определенном энергетическом уровне Е _n (или находятся в квантовом состоянии n )

Собственные функции:

А найдем из усилия нормировки

— плотность вероятности. Из рис. видно, что плотность вероятности меняется в зависимости от n : при n = 1 частица, скорее всего, будет посередине ямы, но не на краях, при n = 2 — будет или в левой или в правой половине, но не посередине ямы и не на краях, и т.д. Т.е нельзя говорить о траектории движения частицы.

Энергетический интервал между соседними уровнями энергии:

При n = 1 имеет наименьшую энергию отличную от нуля

Наличие минимума энергии следует из соотношения неопределенностей, т.к.,

C ростом n расстояние между уровнями уменьшается и при n ® ¥ Е _n практически непрерывны, т.е. дискретность сглаживается, т.е. выполняется принцип соответствия Бора: при больших значениях квантовых чисел законы квантовой механики переходят в законы классической физики.

Общая трактовка принципа соответствия: всякая новая, более общая теория является развитием классической, не отвергает ее полностью, а включает в себя классическую, указывая границы её применимости.

§ 8 Туннельный эффект.

Прохождение частицы через потенциальный барьер

Для классической частицы : при Е > U она пройдет над барьером, при Е U — отразится от него; для квантовой : при Е > U есть вероятность того, что частица отразится, при Е U есть вероятность того, что пройдет сквозь барьер.

Потенциальная энергия:

Уравнение Шредингера: для области 1 и 3 :

для области 2:

Решение этих диф. уравнений;

Для 1;

Для 2;

Для 3:

Т.к. в области 3 возможно распределение только прошедшей волны, то, Þ , В₃=0.

В области 2 решение зависит от соотношений Е > U или Е U . Физический интерес представляет случай Е U .

q = i b , где

Тогда решение уравнения Шредингера запишутся в виде:

Для 1;

Для 2;

Для 3:

Качественный вид функций показан на рис. 2. Из рис. 2 видно, что функция не равна нулю внутри барьера, а в 3 имеет вид волны де Бройля, если барьер не очень широк.

Явление “проникновения” частицы сквозь потенциальный барьер, называется туннельным эффектом. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы можно объяснить используя соотношения неопределенностей: неопределенность импульса D р на отрезке D x = ? составляет . Связанная с этим разбросом в значениях импульса кинетическая энергия может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной энергии барьера.

§9 Линейный гармонический осциллятор

Линейный гармонический осциллятор — система, совершающая одномерное колебательное движение под действием квазиупругой силы — является моделью для изучения колебательного движения.

В классической физике — это пружинный, физический и математический маятники. В квантовой физике — квантовый осциллятор.

Записав потенциальную энергию в виде

Уравнение Шредингера запишется в виде:

Тогда собственные значения энергии:

т.е. энергия квантового осциллятора принимает дискретные значения, т.е. квантуется. Минимальное значение — энергия нулевых колебаний — является следствием состояния неопределенности так же, как и в случае частицы в “потенциальной яме”.

Наличие нулевых колебаний означает, что частицы не могут упасть на дно ямы, т.к. в этом случае был бы точно определен ее импульс p = 0, D p = 0, Þ , D x = ¥ — не соответствует соотношению неопределенностей. Наличие энергии нулевых колебаний противоречит классическим представлениям, по которым E _min = 0. — уровни энергии расположенные на равных расстояниях друг от друга. Из квантового рассмотрения следует, что частицу можно обнаружить вне области. По классическому рассмотрению только в пределах – x £ x £ x (Рис.2).

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

5.1.5 Волновые свойства частиц. Волны де Бройля. Длина волны де Бройля движущейся частицы

Видеоурок: Корпускулярно волновой дуализм. Катющик. Лекция по физике

Лекция: Волновые свойства частиц. Волны де Бройля. Длина волны де Бройля движущейся частицы. Корпускулярно-волновой дуализм. Дифракция электронов на кристаллах

Основой корпускулярно-волнового дуализма является возможность обоснования всех процессов в природе с точки зрения волн и частиц. То же самое можно говорить и о свете. Свет принимается в качестве волны, когда наблюдаются процессы интерференции и дифракции, а при наблюдении фотоэффекта мы становимся свидетелями корпускулярной природы света.

Данная тема позволит определиться нам с природой всех объектов, может, на самом деле не только свет имеет двойственную природу.

Гипотеза де Бройля

О том, что все тела в мире и все частицы имеют двойственную природу, предположил Луи де Бройль. Нам было известно, что свет имеет свой некоторый импульс и энергию, которые определяются с помощью специальных формул. Однако де Бройль предположил обратное: любое движение частицы сопровождается распространением некоторой волны. Определить частоту и её длину можно с помощью значения энергии и импульса.

Ну и, естественно, любая волна, образованная движением частицы, имеет свою энергию и импульс.

Итак, давайте разберем дуализм, относящийся к частице, как волне. Сделаем мы это с помощью электромагнитного излучения. При изучении электромагнитного излучения были сделаны выводы: чем большую длину волны имеет электромагнитная волна, тем меньше у нее наблюдаются корпускулярные свойства. И, наоборот, если волна имеет небольшую длину, её корпускулярные свойства определяются интенсивнее. Итак, давайте рассмотрим зависимость волновых свойств частиц от корпускулярных, перемещаясь по шкале волн.

1. Радиоволны. Как нам известно, данный вид имеет самую большую длину волну, достигающую сотен километров. Поэтому они имеют достаточно выраженные волновые свойства, и практически полное отсутствие корпускулярных свойств. Большая длина волны улучшает дифракционные свойства, в результате чего их лучше всего описывает электродинамика.

2. Волны от видимого излучения и ультрафиолета. Данный тип волн относится к переходному типу — они имеют и волновые и корпускулярные свойства. Корпускулярные свойства света возможны только в том случае, когда частота волн достигает красной границы, а волновые возможны только при небольших щелях, а также достаточно большом расстоянии до рассматриваемого объекта.

3. Рентген, гамма-излучения. Из-за достаточно небольших размеров длины волны, соизмеримой с величиной атома, рассматривать волновые свойства достаточно трудно, однако в качестве частиц с энергией — вполне возможно. Причем данный вид излучений имеет огромную энергию. Поскольку зависимость между длиной волны и частотой — обратная.

Вывод: Чем больше длина волны, тем лучше проявление волновых свойств, чем меньше длина волны — тем лучше проявление корпускулярных свойств.

Дифракция электронов

Масса электронов — это постоянная величина, поэтому мы с легкостью можем рассчитать длину волны движения электронов.

После несложных расчетов можно сделать вывод, что длина волны электрона достаточна для рассмотрения её волновых свойств.

Волновые свойства электронов были обнаружены Дэвиссоном и Джермером в 1927 году. Позднее было открыто, что дифракция на кристаллах возможна и с протонами, нейтронами и многими другими частицами.