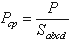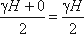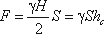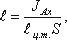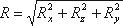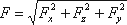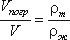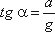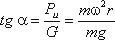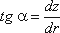Уравнение давление в замкнутом объеме (6 видео)

Содержание

Гидростатическое давление: формула и свойства.
Закон Паскаля для гидростатики.
Определение и формула гидростатического давления
Сила гидростатического давления
Давление в жидкости. Закон Паскаля. Зависимость давления в жидкости от глубины
Уравнение давление в замкнутом объеме
💥 Видео

Видео:Давление газаСкачать

Гидростатическое давление: формула и свойства.

Гидростатическое давление – это давление, производимое на жидкость силой тяжести.

Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматривается практическое приложение этих законов.

Для того, чтобы понять гидростатику необходимо определиться в некоторых понятиях и определениях.

В этой статье мы подготовили для Вас, всю необходимую информацию о гидростатическом давлении, начиная от закона Паскаля и определения формулы гидростатического давления и до свойств давления и применения законов гидростатики в повседневной жизни.

Содержание статьи

Видео:Гидростатическое давлениеСкачать

Закон Паскаля для гидростатики.

В 1653 году французским ученым Б. Паскалем был открыт закон, который принято называть основным законом гидростатики.

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Закон Паскаля легко понимается если взглянуть на молекулярное строение вещества. В жидкостях и газах молекулы обладают относительной свободой, они способны перемещаться друг относительно друга, в отличии от твердых тел. В твердых телах молекулы собраны в кристаллические решетки.

Относительная свобода, которой обладают молекулы жидкостей и газов, позволяет передавать давление производимое на жидкость или газ не только в направлении действия силы, но и во всех других направлениях.

Закон Паскаля для гидростатики нашел широкое распространение в промышленности. На этом законе основана работа гидроавтоматики, управляющей станками с ЧПУ, автомобилями и самолетами и многих других гидравлических машин.

Определение и формула гидростатического давления

Из описанного выше закона Паскаля вытекает, что:

Величина гидростатического давления не зависит от формы сосуда, в котором находится жидкость и определяется произведением

ρ – плотность жидкости

g – ускорение свободного падения

h – глубина, на которой определяется давление.

Для иллюстрации этой формулы посмотрим на 3 сосуда разной формы.

Во всех трёх случаях давление жидкости на дно сосуда одинаково.

Полное давление жидкости в сосуде равно

P0 – давление на поверхности жидкости. В большинстве случаев принимается равным атмосферному.

Сила гидростатического давления

Выделим в жидкости, находящейся в равновесии, некоторый объем, затем рассечем его произвольной плоскостью АВ на две части и мысленно отбросим одну из этих частей, например верхнюю. При этом мы должны приложить к плоскости АВ силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку a. Пусть на эту площадь воздействует сила ΔP.

Тогда гидростатическое давление формула которого выглядит как

представляет собой силу, действующую на единицу площади, будет называться средним гидростатическим давлением или средним напряжением гидростатического давления по площади ΔF.

Истинное давление в разных точках этой площади может быть разным: в одних точках оно может быть больше, в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление Рср будет тем меньше отличаться от истинного давления в точке а, чем меньше будет площадь ΔF, и в пределе среднее давление совпадет с истинным давлением в точке а.

Для жидкостей, находящихся в равновесии, гидростатическое давление жидкости аналогично напряжению сжатия в твердых телах.

Единицей измерения давления в системе СИ является ньютон на квадратный метр (Н/м 2 ) – её называют паскалем (Па). Поскольку величина паскаля очень мала, часто применяют укрупненные единицы:

килоньютон на квадратный метр – 1кН/м 2 = 1*10 3 Н/м 2

меганьютон на квадратный метр – 1МН/м 2 = 1*10 6 Н/м 2

Давление равное 1*10 5 Н/м 2 называется баром (бар).

В физической системе единицей намерения давления является дина на квадратный сантиметр (дина/м 2 ), в технической системе – килограмм-сила на квадратный метр (кгс/м 2 ). Практически давление жидкости обычно измеряют в кгс/см 2 , а давление равное 1 кгс/см 2 называется технической атмосферой (ат).

Между всеми этими единицами существует следующее соотношение:

1ат = 1 кгс/см 2 = 0,98 бар = 0,98 * 10 5 Па = 0,98 * 10 6 дин = 10 4 кгс/м 2

Следует помнить что между технической атмосферой (ат) и атмосферой физической (Ат) существует разница. 1 Ат = 1,033 кгс/см 2 и представляет собой нормальное давление на уровне моря. Атмосферное давление зависит от высоты расположения места над уровнем моря.

Измерение гидростатического давления

На практике применяют различные способы учета величины гидростатического давления. Если при определении гидростатического давления принимается во внимание и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным. В этом случае величина давления обычно измеряется в технических атмосферах, называемых абсолютными (ата).

Часто при учете давления атмосферное давление на свободной поверхности не принимают во внимание, определяя так называемое избыточное гидростатическое давление, или манометрическое давление, т.е. давление сверх атмосферного.

Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным.

Рман = Рабс – Ратм

и измеряют также в технических атмосферах, называемых в этом случае избыточными.

Случается, что гидростатическое давление в жидкости оказывается меньше атмосферного. В этом случае говорят, что в жидкости имеется вакуум. Величина вакуума равняется разнице между атмосферным и и абсолютным давлением в жидкости

Рвак = Ратм – Рабс

и измеряется в пределах от нуля до атмосферы.

Свойства гидростатического давления

Гидростатическое давление воды обладает двумя основными свойствами:
Оно направлено по внутренней нормали к площади, на которую действует;
Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).

Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.

Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на две составляющие – нормальную и касательную. Наличие касательной составляющей из-за отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению жидкости вдоль площадки, т.е. нарушило бы её равновесие.

Поэтому единственным возможным направлением гидростатического давления является его направление по нормали к площадке.

Если предположить что гидростатическое давление направлено не по внутренней, а по внешней нормали, т.е. не внутрь рассматриваемого объекта а наружу от него, то вследствие того, что жидкость не оказывает сопротивления растягивающим усилиям – частицы жидкости пришли бы в движение и её равновесие было бы нарушено.

Следовательно, гидростатическое давление воды всегда направлено по внутренней нормали и представляет собой сжимающее давление.

Из этого же правило следует, что если измениться давление в какой-то точке, то на такую же величину измениться давление в любой другой точке этой жидкости. В этом заключается закон Паскаля, который формулируется следующим образом: Давление производимое на жидкость, передается внутри жидкости во все стороны с одинаковой силой.

На применение этого закона основываются действие машин, работающих под гидростатическим давлением.

Ещё одним фактором влияющим на величину давления является вязкость жидкости, которой до недавнего времени приято было пренебрегать. С появлением агрегатов работающих на высоком давлении вязкость пришлось так же учитывать. Оказалось, что при изменении давления, вязкость некоторых жидкостей, таких как масла, может изменяться в несколько раз. А это уже определяет возможность использовать такие жидкости в качестве рабочей среды.

Видео:Расширение жидкости в ограниченном объёмеСкачать

Давление в жидкости. Закон Паскаля. Зависимость давления в жидкости от глубины

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим отличие жидких и газообразных тел от твердых тел. Если мы захотим изменить объем жидкости, нам придется прикладывать большое усилие, сравнимое с тем, которое мы прикладываем, изменяя объем твердого тела. Даже чтобы изменить объем газа, необходимо весьма серьезное усилие, например насосы и другие механические устройства. Но если мы захотим изменить форму жидкости или газа и будем делать это достаточно медленно, то никаких усилий нам прикладывать не придется. В этом главное отличие жидкости и газа от твердого тела.

Видео:Решение графических задач на тему Газовые законыСкачать

Уравнение давление в замкнутом объеме

Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.

Если эту силу P разделить на площадь дна S_abcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара.

Гидростатическое давление обладает свойствами.

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара площадку S_бок (заштриховано). Гидростатическое давление действует на эту площадку в виде распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим, что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на два составляющих вектора: нормальный R_n (перпендикулярный к заштрихованной площадке) и касательный R_τ к стенке.

Сила нормального давления R_n вызывает в жидкости напряжения сжатия. Этим напряжениям жидкость легко противостоит. Сила R_τ действующая на жидкость вдоль стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая R_τ отсутствует. Отсюда можно сделать вывод первого свойства гидростатического давления.

Свойство 2. Гидростатическое давление неизменно во всех направлениях.

В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет давить сила гидростатического давления, равная произведению соответствующего давления P_x, P_y , P_z на элементарные площади. Обозначим вектора давлений, действующие в положительном направлении (согласно указанным координатам) как P’_x, P’_y, P’_z, а вектора давлений, действующие в обратном направлении соответственно P»_x, P»_y, P»_z. Поскольку кубик находится в равновесии, то можно записать равенства

где γ — удельный вес жидкости;
Δx, Δy, Δz — объем кубика.

Сократив полученные равенства, найдем, что

Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’_z и P»_z, можно пренебречь и тогда окончательно

Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что давления по различным осям одинаковы, т.е.

Это доказывает второй свойство гидростатического давления.

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического давления может быть записано в виде

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила — сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

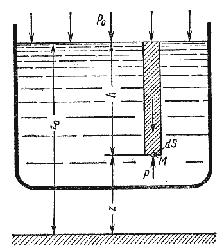
Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P₀ . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P₀. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.

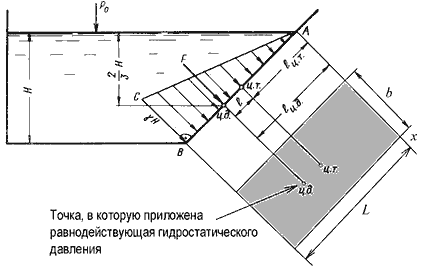
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

Избыточное гидростатическое давление в точке А будет равно

Соответственно давление в точке В:

где H — глубина жидкости в резервуаре.

Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно

Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна

где hc = Н/2 — глубина погружения центра тяжести плоской поверхности под уровень жидкости.

Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

где J_Аx — момент инерции площади S относительно центральной оси, параллельной Аx.

В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.

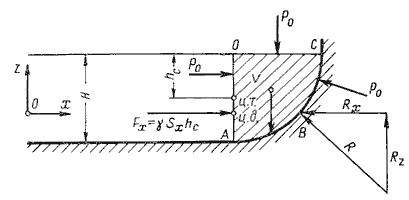
Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскость yOz.

С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на две составляющие R_x и R_z.

Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р₀. Если резервуар открыт, то естественно, что давление Р₀ одинаково со всех сторон и поэтому взаимно уравновешивается.

На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.

Спроецируем все силы на ось Ох:

Теперь спроецируем все силы на ось Оz:

Составляющая силы гидростатического давления по оси O_y обращается в нуль, значит R_y = F_y = 0.

Таким образом, реакция цилиндрической поверхности в общем случае равна

а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F, то делаем вывод, что

Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.

Для однородного тела плавающего на поверхности справедливо соотношение

где: V — объем плавающего тела;
ρ_m — плотность тела.

Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.

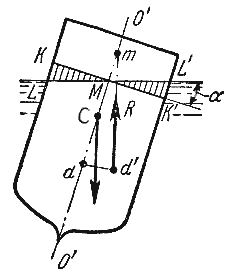
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) — центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O’-O», представляющей ось симметрии судна и называемой осью плавания (рис.2.5).

Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O’-O». Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным — в противном случае.

Теперь рассмотрим условия равновесия судна:

1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h&lt0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.

Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.

Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Рассмотрим два примера такого относительного покоя.

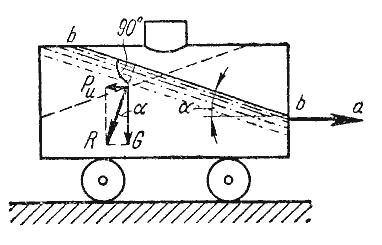
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).

К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции P_u, равная по величине ma. Равнодействующая 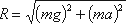этих сил направлена к вертикали под углом α, тангенс которого равен

Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).

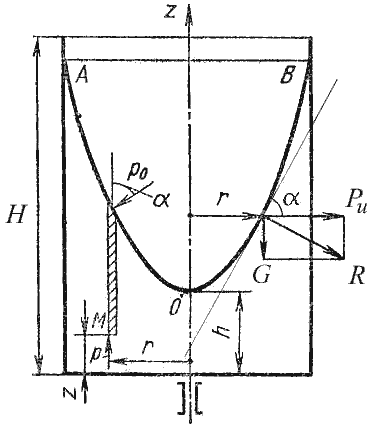
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила P_u = mω 2 r, где r — расстояние частицы от оси вращения, а ω — угловая скорость вращения сосуда.

Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим