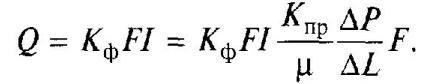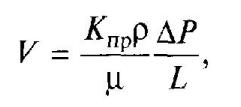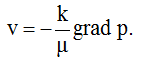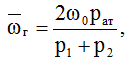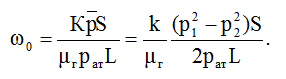Уравнение дарси для фильтрации жидкости и газа в породах с межзерновой пористостью

Видео:Лекция_Проницаемость_Закон_Дарси_09_10_2018Скачать

Линейный закон фильтрации Дарси

В гидродинамике рассматри­вается не движение отдельной частицы или слоя воды, а всей массы воды — фильтрационного потока — условного потока жидкости через пористую или пористо-трещинную среду по сообщающимся порам и трещинам. Фильтрационные потоки подземных вод различаются по характеру движения и подчиняются двум законам. Движение воды параллельно-струйчатого типа называют ламинарным, и оно подчи­няется линейному закону Дарси.

Для простейших условий прямолинейно-параллельного потока линейный закон фильтрации Дарси имеет вид

где Q — расход потока, м 3 /сут; К_ф — коэффициент фильтрации, за­висящий от свойств жидкости и фильтрующей среды, м/сут; F — площадь поперечного сечения потока, м 2 ; ΔН — перепад напоров, м; ΔL — длина участка фильтрационного потока, м.

Согласно закону Дарси, количество воды Q, проходящее через трубку, заполненную дисперсным материалом, прямо пропорцио­нально разности напоров Нв крайних сечениях трубки, прямо про­порционально площади поперечного сечения трубки F, обратно пропорционально длине пути фильтрации L и прямо пропорцио­нально постоянному для данного материала коэффициенту К_ф, характеризующему проницаемость материала, заполняющего трубку.

К основным параметрам фильтрационного потока относятся:

1. расход фильтрационного потока Q — количество воды, прохо­дящее через поперечное сечение потока водоносного слоя за единицу времени, см 3 /с, м 3 /сути т.д.;

2. удельный расход потока q — количество воды Q, проходящее через поперечное сечение потока У 7 при ширине потока 1 м, м 3 :

где F — поперечное сечение потока, м 2 ; l — ширина потока; m — мощность потока, м.

Подставим в формулу Дарси полученное значение:

Поскольку I= (H₁-H₂)/L, при ширине потока 1 м получим

где q — удельный расход потока, м 3 ; L — длина пути фильтрации, м; К_ф — коэффициент фильтрации, м/сут; H₁-H₂ — напор, или разность уровней в крайних сечениях потока, м; I — напорный градиент.

Произведение мощности потока на его водопроницаемость на­зывается водопроводимостью Т потока:

Km = Т или Т = q/I м 2 /сут;

3. пьезометрический напор H подземных вод:

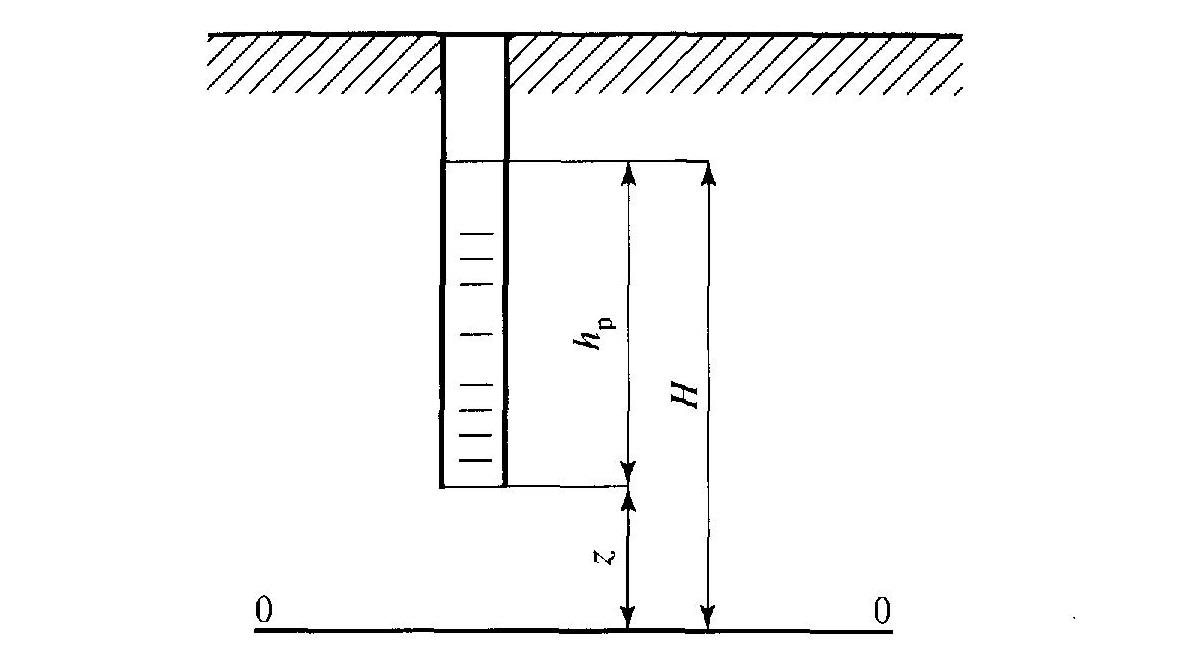
H = P/ρ + z или H = h_p + z

где Р — гидростатическое давление в данной точке потока, МПа, ρ — плотность жидкости, кг/м 3 ; z — гипсометрическая высота данной точки над выбранной плоскостью сравнения, м; Р/ρ или h_p — пьезометрическая высота — та высота, на которую должна подняться вода над данной точкой потока под влиянием гидростатического давления Р в данной точке (энергия давления) (рисунок ниже), равная

где с = 102 (переводной коэффициент значения, МПа).

Видео:Определение коэффициента фильтрации неуплотненного песчаного грунтаСкачать

Схема пьезометрического напора подземных вод (по А.И. Силину-Бекчурину)

Таким образом, пьезометрический напор — это сумма гипсометрической и пьезометрической высот, представляет собой меру энергии потока движущейся воды. При определении напора подземных вод в ка­честве плоскости сравнения может быть взята подошва потока или любая другая горизонтальная поверхность, например уровень Ми­рового океана или забой самой глубокой скважины;

4. напорный градиент (гидравлический уклон) — величина, ха­рактеризующая падение напора ΔH на единицу длины ΔL в направ­лении фильтрации:

где ΔН — перепад напоров, м; Н₁ и Н₂ — напоры в крайних точках потока; L — длина участка фильтрационного потока, м.

Применительно к основному закону фильтрации формула Дарси имеет вид

где К_ф — коэффициент фильтрации, м/сут; F — площадь попереч­ного потока, м 2 ; I—напорный градиент, м;

5. коэффициент фильтрации К_ф— скорость фильтрации при ги­дравлическом уклоне, равном I = 1, характеризующий способность породы пропускать воду. На коэффициент фильтрации влияют вяз­кость и плотность жидкости, минеральный состав пород, температура и др. Коэффициент фильтрации для различных пород имеет разные значения; так, для очень хорошо проницаемых галечников с крупным песком, сильно закарстованных и трещиноватых пород 100-1000 м/сутки и более; для хорошо проницаемых галечников и гравия, крупного песка, среднезернистого песка, закарстованных, трещиноватых пород 100-10; проницаемых галечников и гравия, засоренных мелким песком и глиной, среднезернистого песка, сла- бозакарстованных, слаботрещиноватых пород 10—1; слабо проница­емых тонкозернистых песков, супесей, слаботрещиноватых пород 1-0,1; весьма слабопроницаемых суглинков, глин 0,1 —0,001 м/сут.

В нефтегазовой гидрогеологии коэффициент фильтрации заме­няют коэффициентом проницаемости K_пр, м 2 :

где μ — вязкость жидкости, мПа * с; ρ — плотность жидкости, кг/м 3 ; т.е. коэффициент фильтрации прямо пропорционален проница ёмости фильтрующей среды и обратно пропорционален вязкости фильтрующейся жидкости. Тогда закон Дарси принимает вид

Отсюда выразим скорость фильтрации V, м/сут, через коэффи­циент проницаемости:

где V— скорость фильтрации, м/сут; К_пр — коэффициент проница­емости, м 2 ; ρ — плотность жидкости, кг/м 3 ; μ — вязкость жидкости, мПа * с; ΔР — перепад давлений (напоров), МПа или м; L — длина пути фильтрации, м.

Коэффициенты фильтрации и проницаемости определяют в ла­бораторных условиях, прокачивая через образцы жидкость известной плотности и вязкости. Размерность этих величин м 2 или мкм 2 или дарси (Д);

6. скорость фильтрации V — количество воды, которое про­ходит в единицу времени через единицу поперечного сечения по­тока (м/сут, см/с). Скорость фильтрации Vможно получить, раз­делив расход потока на площадь поперечного сечения фильтру­ющей среды V=Q/F= K_фFI/F, откуда

Так как в практике гидрогеологических исследований вместо К_ф используют коэффициент проницаемости породы, то скорость филь­трации определяют как произведение коэффициента проницаемости на гидравлический уклон:

По данной формуле определяется фиктивная скорость филь­трации, поскольку площадь поперечного сечения потока принята равной площади поперечного сечения породы. В действительности движение воды в породе происходит только по порам и площадь по­тока равна площади пор. Чтобы получить действительную скорость, необходимо расход воды разделить на площадь, занятую порами. Например, применительно к пескам и крупнообломочным породам:

где Q — расход потока, м 3 /сут; F — площадь пор, м 2 ; n — пористость (скважность), выраженная в долях единицы.

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Закон Дарси (движение жидкости и газа в системе)

Движение жидкости и газа на конкретном участке пористой среды происходит под действием градиента давления. Согласно закону Дарси скорость v движения (фильтрации) жидкости (газа) в пористой среде прямо пропорциональна градиенту давления grad р, т.е. перепаду давления р, приходящемуся на единицу длины пути движения жидкости или газа и направлена в сторону падения давления:

В этой форме записи закона Дарси коэффициент пропорциональности равен подвижности жидкости, т.е. отношению проницаемости k породы к вязкости жидкости m.

Скорость фильтрации определяется отношением расхода жидкости w, протекающей через образец породы, к площади поперечного сечения образца S, расположенного перпендикулярно к направлению потока:

V=w/S

Принимая градиент давления на образце породы длиной L величиной постоянной

grad p=Δp/L

закон Дарси обычно записывают в виде формулы:

w=k(ΔpS / μL)

Истинная скорость движения жидкости в пористой среде больше скорости фильтрации, так как на самом деле жидкость движется не по всему сечению образца, а лишь по поровым каналам, суммарная площадь которых S1 меньше общей площади образца S:

Здесь m_дин – динамическая пористость образца породы.

т.е. истинная скорость движения жидкости в пористой среде равна отношению скорости фильтрации к динамической пористости коллектора.

При фильтрации через пористую среду газа его объемный расход по длине образца изменяется в связи с уменьшением давления. Информация предоставленна только для ознакомления с онлайн казино и не является призывом к игре. В таком формате доступны все наиболее популярные азартные игры, включая рулетку, блэкджек и баккара. Вы можете играть в казино с мобильного телефона и получить бонус, мобильная версия Casino X имеет большое количество преимуществ для игроков. Ведь в теперешнее время вулканов столико развилось, и каждый хвалит себя. Получить бонус Казино CasinoX широко известно профессиональным геймерам и новичкам. Казино Casino X давало купон на бездепозитный бонус. Среднее давление по длине образца пористой породы принимают равным:

где р1 и р2 – соответственно давление газа на границах образца.

Средний объемный расход газа wг при его изотермическом расширении по длине образца можно оценить по формуле, вытекающей из закона Бойля-Мариотта для идеальных газов:

где w₀ – расход газа при атмосферном давлении р_ат.

Закон Дарси при фильтрации газа записывается в виде формулы:

Здесь m_г – вязкость газа.

Закон Дарси – основной закон подземной гидродинамики – науки, на которой базируются методы проектирования и контроля процессов разработки нефтяных и газовых месторождений и методы промысловых исследований скважин и пластов.

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Модели пористых сред. Закон Дарси

Вы будете перенаправлены на Автор24

Видео:Основные физические свойства жидкости и газаСкачать

Закон Дарси. Техническая реализация закона. Способы записи закона Дарси

Анри Дарси получил известность благодаря сооружению водопровода в городе Дижон. В 1856 году он смог обосновать закон, который связывал скорость фильтрации жидкости с градиентом давления. В последние годы своей жизни Дарси занимался опытами в области законов движения воды в открытых каналах. Благодаря его исследованиям удалось сделать полезные выводы относительно воздействия профиля русла на коэффициенты сопротивления движению воды.

Закон Дарси – это закономерность фильтрации газов и жидкостей в пористой среде.

Закон Дарси устанавливает линейную зависимость между гидравлическим градиентом (перепад давления, уклон) и объемным расходом газа или жидкости в таких пористых структурах, как:

1. Мелкозернистые грунты.
2. Глинистые грунты.
3. Песчаные грунты.

Данный закон можно выразить через следующую формулу:

Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ

где, Q — объемный расход жидкости; v — скорость фильтрации жидкости или газа; F — эффективная площадь рассматриваемого объема пористой среды (площадь поперечного сечения образца); k — коэффициент проницаемости пористой среды; р1, р2 — давления, которые созданы на концах испытуемого образца; u — абсолютная вязкость (для жидкости); L — длина фильтрующей части породы.

Коэффициент фильтрации в законе Дарси представляет собой одновременно характеристики среды и жидкости. Значение данного коэффициента зависит от следующих факторов: вязкости жидкости, размер частиц, пористость среды, форма частиц, степень шероховатости. Он применяется, как правило, в гидротехнических расчетах, в которых жидкостью является вода.

Готовые работы на аналогичную тему

При изучении течений газов и жидкостей в пористой среде, в фундаментальной механике сплошных сред, используется дифференциальная форма закона Дарси, которая выглядит следующим образом:

Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ

где, P — внешнее давление; p — плотность флюида; n — динамическая вязкость флюида; g — ускорение свободного падения; z — вертикальная координата; K — коэффициент проницаемости.

Закон Дарси также возможно представить в виде уравнения баланса сил:

Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ

где, f — поле внешних сил; n — динамическая вязкость газа или жидкости; K = nk / pg — коэффициент проницаемости.

Таким образом, полную систему уравнений фильтрации, включающую условие не сжимаемости, можно записать следующим образом:

Рисунок 4. Система уравнений. Автор24 — интернет-биржа студенческих работ

При условии, что поле скорости фильтрации имеет скалярный потенциал (то есть коэффициент проницаемости постоянен), то закон Дарси можно записать в форме уравнения Лапласа:

Рисунок 5. Уравнение Лапласа. Автор24 — интернет-биржа студенческих работ

Из условия не сжимаемости получается уравнение Лапласа с граничным условием:

Рисунок 6. Уравнение. Автор24 — интернет-биржа студенческих работ

где n — вектор нормали к поверхности.

Техническая реализация закона Дарси происходит при помощи лабораторной установки, использующейся для изучения реальных и модельных характеристики пористых пород. Схема данной установки изображена на рисунке ниже.

Рисунок 7. Схема установки. Автор24 — интернет-биржа студенческих работ

1 — насос с жидкостью или баллон с газом; 2 — вентиль; 3 — регулятор давления; 4 — входной манометр; 5 — модель пористой среды; 6 — выходной манометр; 7 — расходомер.

Закон Дарси используется для расчета фильтрации жидкостей, которые подчиняются закону Навье-Стокса. Для фильтрации некоторых видов нефтей связь между скоростью фильтрации и градиентом давления может быть нелинейной. Для ньютоновских жидкостей применение закона Дарси ограничено маленькими скоростями фильтрации (число Рейнольдса).

Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Модели пористых сред

Пористая среда – это твердое тело, пронизанное системой пустот, которые имеют нерегулярный характер и делают среду проницаемой для газов и жидкостей.

Первые исследования порового пространства осуществлялись при помощи идеализированных моделей грунта, называемых:

1. Идеальным грунтом.
2. Фиктивным грунтом.

Под идеальным грунтом понимается модель пористой среды, каналы которой представляют собой пучки тонких капилляров в виде цилиндров, имеющих параллельные оси. Фиктивный грунт — модель пористой среды, которая состоит из шариков одинакового диаметра. Американский гидрогеолог Слихтер смог упростить теорию фильтрации, что позволило сравнить течение жидкости по порам с движением жидкости по цилиндрическим трубкам. Слихтер, основываясь на модели фиктивного грунта, рассмотрел геометрическую задачу, что позволило связать пористость с углами, которые образованы радиусами соприкасающихся между собой шаров — моделирующих пористую среду, при различной упаковке.

Если объем пустот при воздействии нагрузок не деформируется, то среда – недеформируемая, если деформируется и после снятия нагрузки не восстанавливается, то среда – деформируемая, в случае, если деформируется, но при снятии нагрузки восстанавливается – среда упругая.

Геометрическим параметром, который характеризует размер порового пространства является эффективный диаметр. Данный показатель определяется при помощи механического анализа грунта. Эффективный диаметр, который слагает пористую среду, представляет собой диаметр шаров, которые образовывают фиктивный грунт, в котором гидравлическое давление (оказываемое фильтрующей жидкостью) в эквивалентном и реальном фиктивном грунте одинаково. Эффективный диаметр можно выразить следующей формулой:

Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ

где, di — средний диаметр i фракции; n — число частиц фракции.

Использование закона Дарси и моделей пористых систем в нефтегазовой промышленности позволяет уже на ранних стадиях проектирования разработки месторождения нефти или природного газа качественно определить основные параметры работы, что будет способствовать техническому и экономическому успеху.

📸 Видео

Газовые Законы и Правила. Уравнение Менделеева-Клапейрона. Пример расчета объема газа при Р атм.Скачать

Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Решение графических задач на тему Газовые законыСкачать

Относительная проницаемостьСкачать

Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Уравнение состояния идеального газа. 10 класс.Скачать

Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

11-1. Грунтоведение. Физические свойства грунтов. Плотность, водопроницаемость грунтов. Закон Дарси.Скачать

МОДЕЛИРОВАНИЕ МНОГОФАЗНЫХ ФИЛЬТРАЦИОННЫХ ТЕЧЕНИЙСкачать

Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Гидродинамика, теплопередача и механика грунтов в COMSOL Multiphysics®. Версия 5.6Скачать