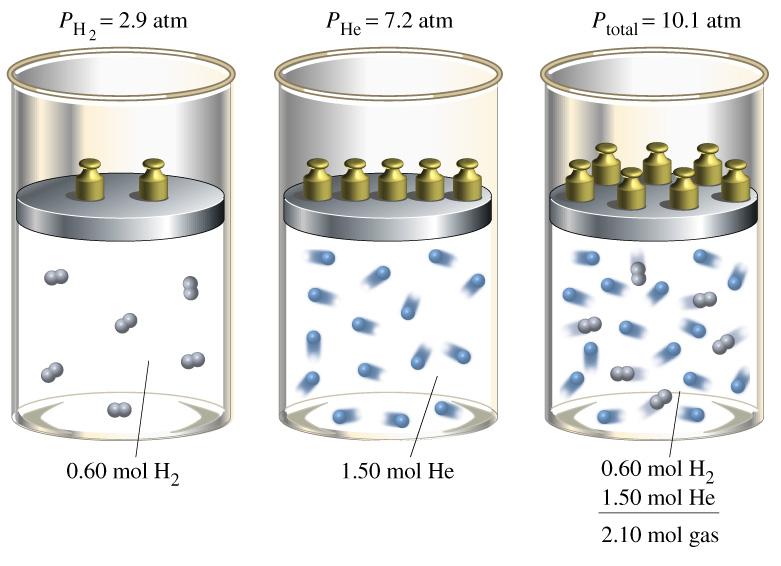
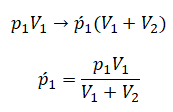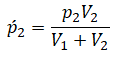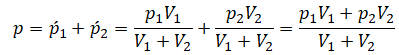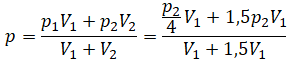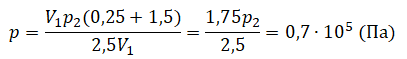Уравнение дальтона для смеси газов (6 видео)

Закон Дальтона

В природе и в технике мы очень часто имеем дело не только с одним чистым газом, но со смесью нескольких газов. Например воздух, это смесь азота, кислорода, аргона, углекислого газа и других газов. От чего зависит давление смеси газов?

В 1801 г. Джон Дальтон установил, что давление смеси нескольких газов равно сумме парциальных давлений всех газов, составляющих смесь.

Этот закон получил название закона парциальных давлений газов

Закон Дальтона Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.

Закон Дальтона устанавливает, что давление смеси (идеальных) газов составляет сумму парциальных давлений компонент смеси (парциальное давление компоненты – это давление, которое компонента оказала бы, если бы она одна занимала все пространство, занятое смесью). Этот закон указывает, что на каждую компоненту не воздействует присутствие других компонент и свойства компоненты в смеси не меняются.

Содержание

Два закона Дальтона
Уравнение закона Дальтона
Закон Дальтона для смеси газов: примеры решения задач
Идеальные газы
Парциальное давление компонента
Формулировка закона Дальтона
Примеры решения задач
Закон Дальтона
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Применение закона Дальтона при решении задач
💥 Видео

Два закона Дальтона

Закон 1 Давление смеси газов равно сумме их парциальных давлений. Из этого следует, что парциальное давление компонента газовой смеси равно произведению давления смеси на молярную долю этого компонента.

Закон 2 Растворимость компонента газовой смеси в данной жидкости при постоянной температуре пропорциональна парциальному давлению этого компонента и не зависит от давления смеси и природы других компонентов.

Законы сформулированы Дж. Дальтоном соотв. в 1801 и 1803.

Уравнение закона Дальтона

Как уже отмечалось, отдельные компоненты смеси газов считаются независимыми. Поэтому каждая компонента создает давление:

[ p = p_i k T quad left(1right), ]

а полное давление равно сумме давлений компонент:

[ p = p_ k T + p_ k T + cdots + p_ k T = p_ + p_ + cdots + p_ quad left(2right),]

где ( p_i ) — парциальное давление i газовой компоненты. Это уравнение — закон Дальтона.

При больших концентрациях, больших давлениях закон Дальтона не выполняется в точности. Так как проявляется взаимодействие между компонентами смеси. Компоненты перестают быть независимыми. Дальтон объяснил свой закон с помощью атомистической гипотезы.

Пусть имеется i компонент в смеси газов, тогда уравнение Менделеева — Клайперона будет иметь вид:

где ( m_i ) — массы компонент смеси газа, ( _i ) — молярные массы компонент смеси газа.

Если ввести ( leftlangle mu rightrangle ) такую, что:

то уравнение (3) запишем в виде:

Закон Дальтона можно записать в виде:

Следствием закона Дальтона можно считать следующее выражение:

[ p_i=x_ip quad left(7right), ]

где ( x_i-молярная концентрация i-го ) газа в смеси, при этом:

где ( _i ) — количество молей ( i-го ) газа в смеси.

Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Закон Дальтона для смеси газов: примеры решения задач

Газовые смеси, в которых компоненты не взаимодействуют друг с другом, могут быть описаны с помощью закона Дальтона. Он связывает парциальные давления компонентов и их мольные доли в одно равенство. Рассмотрим подробнее этот закон, а также покажем, как его можно использовать, на конкретных примерах.

Видео:Введение в парциальное давление | Газы.Молекулярно-кинетическая теория | ХимияСкачать

Идеальные газы

Закон Дальтона в физике оказывается справедливым исключительно для идеальных газов. Под таковыми понимают газы, составляющие частицы которых (атомы, молекулы) не взаимодействуют между собой. Для идеального газа при неизменном числе молекул (атомов) в нем (n = const) справедливо равенство, связывающее три макроскопических параметра (давление P, объем V и температуру T):

P*V = n*R*T, R = 8,314 Дж/(К*моль) — постоянная величина.

Все реальные газы при давлениях в несколько атмосфер и температурах порядка комнатной и выше можно с хорошей точностью считать идеальными, то есть для них справедливо приведенное равенство.

Видео:Физика. МКТ: Смеси газов. Закон Дальтона. Центр онлайн-обучения «Фоксфорд»Скачать

Парциальное давление компонента

Чтобы понять суть закона Дальтона, необходимо разобраться с понятием «парциальное давление».

Поскольку молекулы разных газов не «чувствуют» друг друга, для каждого химического компонента i в газовой смеси будет справедливо равенство:

То есть можно считать каждый компонент независимым от других. Поскольку его молекулы занимают весь объем V и имеют температуру T, характерную для всей смеси, то отсюда и следует справедливость записанного выражения.

Давление P_i называется парциальным для i-го компонента. Иными словами, парциальное давление — это то давление, которое только i-й компонент создает на стенки сосуда. Парциальным оно называется потому, что является частью от общего давления, или его порцией.

Видео:смесь газов Закон Дальтона задача 1Скачать

Формулировка закона Дальтона

В первые годы XIX века, занимаясь изучением поведения различных газовых смесей, британский ученый Джон Дальтон установил следующий факт: если суммировать все парциальные давления компонентов газовой смеси, то получится общее давление, которое можно измерить барометром, манометром или другим предназначенным для этого прибором. Это и есть закон Дальтона. Запишем его в виде математического равенства:

Понять, почему это равенство справедливо, можно, если вспомнить, что компоненты смеси создают давление независимо друг от друга.

Учитывая, что парциальное давление P_i прямо пропорционально количеству вещества n_i компонента i, что справедливо всегда, когда T=const и V = const, тогда приходим к еще одному равенству:

Величина x_i называется мольной долей. С атомными процентами a_i компонента она связана простым соотношением:

Выражение, которое позволяет определить мольную долю компонента через его парциальное давление и наоборот, также называется законом Дальтона.

Следует не забывать, что рассмотренный закон справедлив не только в случае идеальных газов, но и в случае отсутствия химических реакций в них. Последние приводят к изменениям компонентного и мольного состава, что нарушает закон для давления газовой смеси.

Видео:Объемные отношения газов при химических реакциях. 8 класс.Скачать

Примеры решения задач

В этом пункте рассмотрим примеры применения закона Дальтона для решения практических задач.

Задача 1. Необходимо определить парциальное давление трех основных компонентов в сухом воздухе.

Из литературных данных можно узнать, что поскольку воздух является сухим, то основными его компонентами будут азот (около 78 %), кислород (около 21 %) и благородный газ аргон (около 1 %). Учитывая, что общее давление воздуха на уровне моря равно 1 атмосфере, и переводя атомные проценты в мольные доли, получим значения парциальных давлений для каждого компонента:

P_N2 = 1 *0,78 = 0,78 атм.

Задача 2. Есть два баллона с чистыми газами. Первый баллон содержит азот с температурой 300 К, объемом в 10 литров и давлением в 2 атмосферы. Второй баллон содержит кислород с температурой 300 К, но имеющий объем 15 литров и давление 1,5 атмосферы. Оба баллона соединили друг с другом. Необходимо рассчитать парциальное давление каждого компонента в полученной смеси.

Решать эту задачу начнем с вычисления количества вещества для азота и кислорода. Используя уравнение для идеального газа, получим:

Когда два баллона соединят, произойдет перемешивание газов так, что каждый компонент займет весь объем двух баллонов. Общее давление, которое будет в системе, можно рассчитать, пользуясь также уравнением состояния идеального газа:

P_tot = n*R*T/V_tot = 1,726*8,314*300/(2,5*10 -2 ) = 172199,568 Па или 1,7 атм.

Теперь можно применить формулы закона Дальтона, чтобы рассчитать парциальные давления кислорода и азота:

Отношение полученных парциальных давлений газов равно отношению количеств вещества для них.

Видео:Основы теплотехники. Газовые смеси. Закон Дальтона.Скачать

Закон Дальтона

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Давление смеси газов равно сумме их парциальных давлений.

К примеру, давление воздуха складывается из давления азота, кислорода, углекислого газа, водяного пара и т. д.

Парциальное давление — давление, которое производил бы данный газ, если бы другие газы отсутствовали.

Видео:Лекция №3. СМЕСЬ ИДЕАЛЬНЫХ ГАЗОВСкачать

Применение закона Дальтона при решении задач

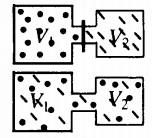
Самая популярная задача на закон Дальтона, это случай, когда газы находятся в сосудах, соединенных трубкой с краном. По условию этой задачи нужно найти давление, которое установится после того, как этот кран будет открыт.

После открытия крана первый и второй газы заполнят оба сосуда. Используем закон Бойля — Мариотта для первого газа (так как температура остается постоянной):

Этот же закон можем применить для второго газа. Тогда мы получим:

Применим закон Дальтона и получим:

Пример №1. Два сосуда соединены трубкой с краном. Определить давление, которое установится после того, как кран будет открыт. Считать, что объем второго сосуда в 1,5 раза больше первого. Давление во втором сосуде составляет половину от атмосферного давления. В первом сосуде оно меньше в 4 раза.

Проанализируем условия задачи и запишем:

Теперь можем применить выведенную ранее формулу:

Преобразуем выражение и найдем установившееся давление:

Алгоритм решения

Решение

Запишем исходные данные:

После того, как открыли кран между 2 и 3 сосудом, объем возрос вдвое, и давление распределилось по нему равномерно. Согласно закону Дальтона, оно стало равным сумме давлений, оказываемых газами в количестве вещества ν₂ и ν₃. Так как объем после открытия крана увеличивается вдвое, то парциальное давление каждого из количества вещества равно половине исходного давления:

p 23 = p 2 . . + 3 p 2 . . = 2 p

Потом кран 2–3 закрыли, но открыли кран 1–2. Применим закон Дальтона, получим:

p 12 = 2 p 2 . . + p 2 . . = 3 p 2 . .

Теперь применим закон Менделеева — Клапейрона:

Для начального состояния газа в 1 сосуде:

Для конечного состояния газа в 1 сосуде:

3 p 2 . . V = ν 2 R T

Так как температура и объем неизменны, но давление увеличилось в 1,5 раза, то и количество газа в первом сосуде увеличилось в 1,5 раза.

pазбирался: Алиса Никитина | обсудить разбор | оценить

В сосуде неизменного объёма при комнатной температуре находилась смесь неона и аргона, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль аргона. Как изменились в результате парциальное давление неона и давление смеси газов, если температура газов в сосуде поддерживалась неизменной?

Для каждой величины определите соответствующий характер изменения:

увеличилась
уменьшилась
не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Сначала парциальное давление неона и аргона равно. Это объясняется тем, что давление газов при неизменном количестве вещества зависит только от объема и температуры. Эти величины постоянны.

Когда из сосуда выпустили половину газовой смеси, в нем оказалось по половине моля каждого из газов. Затем в сосуд впустили 1 моль аргона. Следовательно, в сосуде стало содержаться 0,5 моль неона и 1,5 моль аргона. Запишем уравнение Менделеева — Клапейрона:

Из уравнения видно, что давление и количество вещества — прямо пропорциональные величины. Следовательно, если количество неона уменьшилось, то его парциальное давление тоже уменьшилось.

Общая сумма количества вещества равна сумме количеств вещества 1 (неона) и 2 (аргона): 0,5 + 1,5 = 2 (моль). Изначально в сосуде тоже содержалось 2 моль газа. Так как количество вещества, температура и объем сохранились, давление тоже осталось неизменным.

pазбирался: Алиса Никитина | обсудить разбор | оценить