- Ни одной
- Одной
- Ни одного решения
- Одно решение
- Два решения
- Больше двух решений
- Арккосинус. Решение уравнения cos x=a
- п.1. Понятие арккосинуса
- п.2. График и свойства функции y=arccosx
- п.3. Уравнение cosx=a
- п.4. Формула арккосинуса отрицательного аргумента
- п.5. Примеры
- Уравнение cos x = a
- Просмотр содержимого документа «Уравнение cos x = a»
- 💡 Видео
Уравнение cos x = a
Сколько точек пересечения с тригонометрической окружностью имеет прямая x=m в зависимости от значения m:
Ни одной
Одной
Уравнение cos x = a
Выберите из списка решение уравнения
$x=pmfrac+2pi n, n epsilon Z$
$x=frac + pi n, n epsilon Z$
$x=frac +pi n, n epsilon Z$
$x= pm frac+2pi n, n epsilon Z$
$x=pmfrac+2pi n,n epsilon Z$
$x = frac + 2pi n, n epsilon Z$
Уравнение cos x = a
Поставьте в соответствие каждому уравнению его решение.
Уравнение cos x = a
Подчеркните верное равенство
- $arccos (-frac)=-frac$
- $arccos (-frac)= frac$
- $arccos (-frac)= -frac$
- $arccos (-frac)= frac$
- $arccos (-frac)= frac$
Уравнение cos x = a
Сколько точек на отрезке $ [-pi; pi] $имеет уравнение $2 cos (2x) = sqrt$
Уравнение cos x = a
Решите уравнение $cos alpha =-frac$. Заполните пропуски в ответе
Ответ: $alpha = pm frac+cpi k, k epsilon Z$
Уравнение cos x = a
Расположите значения арккосинусов в порядке возрастания.
Уравнение cos x = a
Выделите цветом верные равенства
- cos(arccos(−0,4))=−0,4
- arccos(cos2)=2
- cos(arccos2)=2
- arccos(cos(−2))=−2
- cos(arccos(0,2))=0,2
Уравнение cos x = a
Найдите для каждого уравнения количество решений на отрезке $[0; 2π]$.
Ни одного решения
Одно решение
Два решения
Больше двух решений
Уравнение cos x = a
Решите уравнение $cos (2-3x) = cos (4x -5)$
В ответ запишите наименьший положительный корень.
Уравнение cos x = a
Решите уравнение $(4cos x +1)(2 cos x +3)$
Выберите верный ответ.
$begin x = pm (pi — arccos(frac)) + 2 pi n,n epsilon Z \ x = pm (pi — arccos (frac))+ 2 pi n, n epsilon Z end$
$begin x=pm (arccos (frac)) + 2pi n, n epsilon Z \ x = pm (pi — arccos(frac)) + 2 pi n, n epsilon Z end$
$x = pm arccos (frac) + 2pi n , n epsilon Z$
$x = pm (pi — arccos (frac)) + 2 pi n, n epsilon Z$
$begin x = pm arccos (frac) + 2 pi n, n epsilon Z \ x = pm arccos (frac) + 2pi n, n epsilon Z end $
Видео:§33 Уравнение cos x = aСкачать

Арккосинус. Решение уравнения cos x=a
п.1. Понятие арккосинуса
В записи (y=cosx) аргумент x — это значение угла (в градусах или радианах), функция y – косинус угла, действительное число в пределах [-1;1]. Т.е., по заданному углу мы находим косинус.
Можно поставить обратную задачу: по заданному косинусу найти угол. Но одному значению косинуса соответствует бесконечное количество углов. Например, если (cosx=1), то (x=2pi k, kinmathbb); (cosx=0), то (x=fracpi2+pi k, kinmathbb) и т.д.
Поэтому, чтобы построить однозначную обратную функцию, ограничим значения углов x отрезком, на котором косинус принимает все значения из [-1;1], но только один раз: (0leq xleq pi) (верхняя половина числовой окружности).
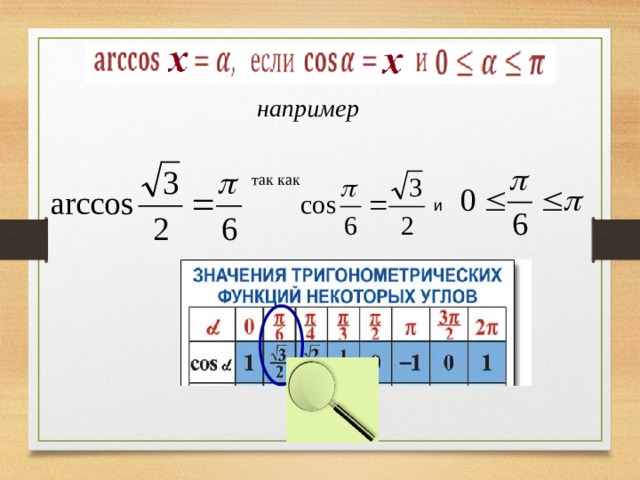
(arccosfrac12=fracpi3, arccosleft(-frac<sqrt>right)=frac)
(arccos2) – не существует, т.к. 2> 1
п.2. График и свойства функции y=arccosx
1. Область определения (-1leq xleq1) .
2. Функция ограничена сверху и снизу (0leq arccosxleq pi) . Область значений (yin[0;pi])
3. Максимальное значение (y_=pi) достигается в точке x =-1
Минимальное значение (y_=0) достигается в точке x =1
4. Функция убывает на области определения.
5. Функция непрерывна на области определения.
п.3. Уравнение cosx=a
 | Значениями арккосинуса могут быть только углы от 0 до π (180°). А как выразить другие углы через арккосинус? |
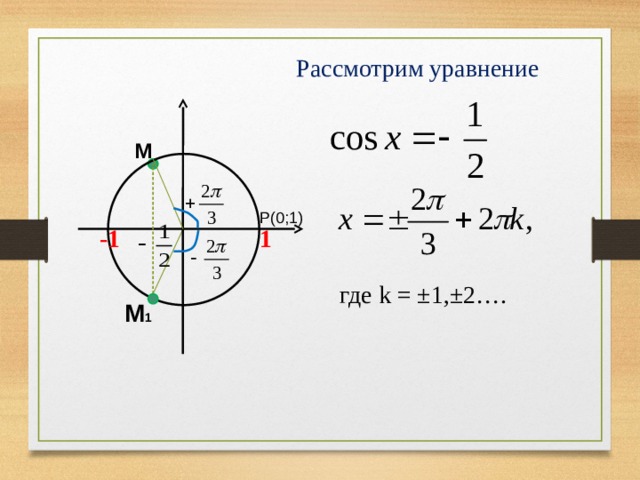
Углы в нижней части числовой окружности записывают через отрицательный арккосинус. А углы, которые превышают π по модулю, записывают через сумму арккосинуса и величины, которая ‘не помещается» в область значений арккосинуса.
1) Решим уравнение (cosx=frac12).
Найдем точку (frac12) в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках, соответствующих углам (pmfracpi3) — это базовые корни.
Если взять верхний корень (fracpi3) и прибавить к нему полный оборот (fracpi3+2pi=frac), косинус полученного угла (cosfrac=frac12), т.е. (frac) также является корнем уравнения. Корнями будут и все другие углы вида (fracpi3+2pi k) (с любым количеством добавленных или вычтенных полных оборотов). Аналогично, корнями будут все углы вида (-fracpi3+2pi k).
Получаем ответ: (x=pmfracpi3+2pi k)
Заметим, что полученный ответ является записью вида
(x=pm arccosfrac12+2pi k)
А т.к. арккосинус для (frac12) точно известен и равен (fracpi3), то мы его и пишем в ответе.
Но так бывает далеко не всегда.
2) Решим уравнение (cosx=0,8)
 | Найдем точку 0,8 в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках. По определению верхняя точка – это угол, равный arccos0,8. Тогда нижняя точка – это тот же угол, но отложенный в отрицательном направлении обхода числовой окружности, т.е. (–arccos0,8). Добавление или вычитание полных оборотов к каждому из решений даст другие корни. Получаем ответ: (x=pm arccos0,8+2pi k) |
п.4. Формула арккосинуса отрицательного аргумента
Докажем полезную на практике формулу для (arccos(-a)).
 | По построению: $$ begin angle DA’O=angle BAO=angle CAO=90^\ OD=OB=OC=1\ OA’=OA=a end Rightarrow $$ (по катету и гипотенузе) begin Delta DA’O=Delta BAO=Delta CAORightarrow\ Rightarrow angle DOC=angle A’OA-alpha+alpha=angle A’OA=180^=pi\ -arccosa+pi=arccos(-a) end |
п.5. Примеры
Пример 1. Найдите функцию, обратную арккосинусу. Постройте графики арккосинуса и найденной функции в одной системе координат.
Для (y=arccosx) область определения (-1leq xleq 1), область значений (0leq yleq pi).
Обратная функция (y=cosx) должна иметь ограниченную область определения (0leq xleq pi) и область значений (-1leq yleq 1).
Строим графики:
Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.
Пример 2. Решите уравнения:
a) (cos x=-1) (x=pi+2pi k) | б) (cos x=frac<sqrt>) (x=pmfracpi4+2pi k) |
в) (cos x=0) (x=pmfracpi2+2pi k=fracpi2+pi k) | г) (cos x=sqrt) (sqrtgt 1, xinvarnothing) Решений нет |
д) (cos x=0,7) (x=pm arccos(0,7)+2pi k) | e) (cos x=-0,2) (x=pm arccos(-0,2)+2pi k) |
Пример 3. Запишите в порядке возрастания: $$ arccos0,8; arccos(-0,5); arccosfracpi7 $$
 | Способ 1. Решение с помощью числовой окружности |
Отмечаем на оси косинусов (ось OX) точки с абсциссами 0,8; -0,5; (fracpi7approx 0,45)
Значения арккосинусов (углы) считываются на верхней половине окружности: чем меньше косинус (от 1 до -1), тем больше угол (от 0 до π).
Получаем: (angle A_1OAltangle A_2OAangle A_3OA)
$$ arccos0,8lt arccosfracpi7lt arccos(-0,5) $$

Отмечаем на оси OX аргументы 0,8; -0,5; (fracpi7approx 0,45). Восстанавливаем перпендикуляры на кривую, отмечаем точки пересечения. Из точек пересечения с кривой восстанавливаем перпендикуляры на ось OY — получаем значения арккосинусов по возрастанию: $$ arccos0,8lt arccosfracpi7lt arccos(-0,5) $$
Арккосинус – функция убывающая: чем больше аргумент, тем меньше функция.
Поэтому располагаем данные в условии аргументы по убыванию: 0,8; (fracpi7); -0,5.
И записываем арккосинусы по возрастанию: (arccos0,8lt arccosfracpi7lt arccos(-0,5))
Пример 4*. Решите уравнения:
(a) arccos(x^2-3x+3)=0) begin x^2-3x+3=cos0=1\ x^2-3x+2=0\ (x-2)(x-1)=0\ x_1=1, x_2=2 end Ответ:
(б) arccos^2x-arccosx-6=0)
( text -1leq xleq 1 )
Замена переменных: (t=arccos x, 0leq tleq pi)
Решаем квадратное уравнение: $$ t^2-t-6=0Rightarrow (t-3)(t+2)=0Rightarrow left[ begin t_1=3\ t_2=-2lt 0 — text end right. $$ Возвращаемся к исходной переменной: begin arccosx=3\ x=cos3 end Ответ: cos3
(в) arccos^2x-pi arccosx+frac=0)
( text -1leq xleq 1 )
Замена переменных: (t=arccos x, 0leq tleq pi)
Решаем квадратное уравнение: begin t^2-pi t+frac=0\ D=(pi^2)-4cdot frac=frac, sqrt=fracpi3\ left[ begin t_1=frac=fracpi3\ t_2=frac=frac end right. Rightarrow left[ begin arccosx_1=fracpi3\ arccosx_2=frac end right. Rightarrow left[ begin x_1=cosleft(fracpi3right)=frac12\ x_2=cosleft(fracright)=-frac12 end right. end Ответ: (left)
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Уравнение cos x = a
Первый урок в теме «Тригонометрические уравнения». Тема урока «Уравнение cos x = a»
Просмотр содержимого документа
«Уравнение cos x = a»
Уравнение есть равенство, которое еще не является истинным, но которое стремятся сделать истинным, не будучи уверенным, что этого можно достичь.

Косинусом угла α называется абсцисса точки
значит из определения косинуса
Пример 1 . cos x = 2,5
Уравнение не имеет корней, т.к. 2,51
Пример 2 . cos x = -1,5 т
Уравнение не имеет корней, т.к. -1,5
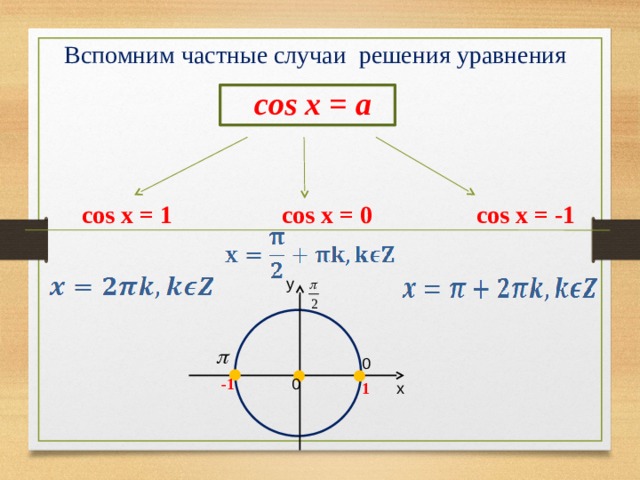
Вспомним частные случаи решения уравнения
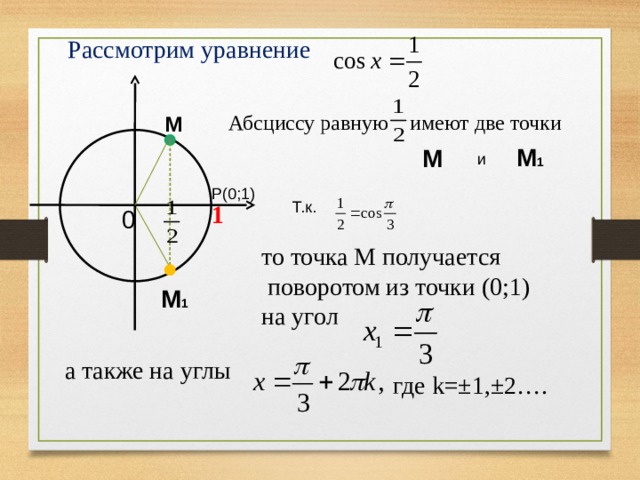
Абсциссу равную имеют две точки
то точка М получается
поворотом из точки (0;1)
а также на углы
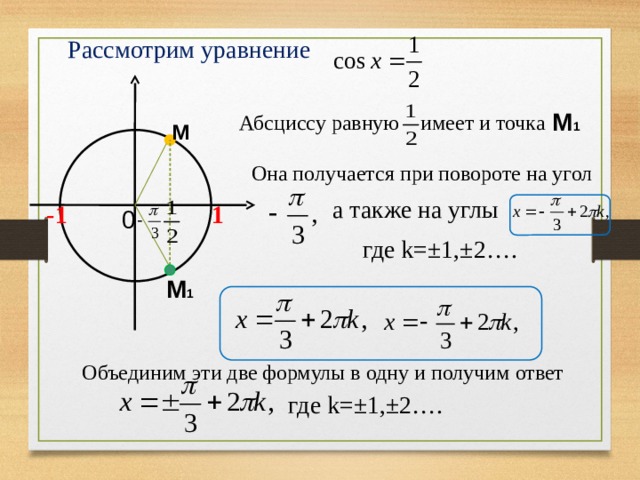
Абсциссу равную имеет и точка
Она получается при повороте на угол
а также на углы
Объединим эти две формулы в одну и получим ответ
Понятие арккосинуса числа x
Число называют арккосинусом и записывают
Число называют арккосинусом и записывают
Арккосинусом числа x [-1;1] называют такое
число , косинус которого равен x
Решения уравнения вида cos x = a , где
💡 Видео
КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать

Уравнение косинус. Арккосинус. Видеоурок 28. Алгебра 10 классСкачать

Тригонометрические уравнения. Алгебра 10 класс. cos x = a.Скачать

Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать

Алгебра 10 класс (Урок№41 - Уравнение cos x = a.)Скачать

Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

10 класс - Алгебра - Тригонометрические уравнения. Арккосинус. Решение уравнения cos t = aСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Алгебра 10 класс. 18 октября. Что такое arccos арккосинусСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

Решение уравнений вида cos x =aСкачать

Решение уравнения вида cosx=aСкачать

Уравнение cos x=a | тригонометрическое уравнение | алгебра 10 класс | МегаШкола | Уравнение с cosxСкачать

Уравнение cosx =aСкачать

Арккосинус. Решение уравнения cos t = а | Алгебра 10 класс #26 | ИнфоурокСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Как найти значения аркфункций? (Перечень, ДВИ)Скачать

Тригонометрические уравнения. Косинус.Скачать