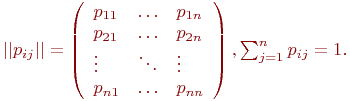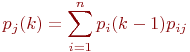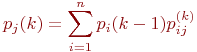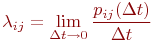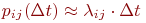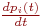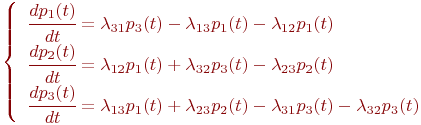Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова — старшего (1856 — 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 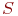
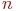
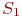
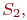
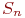
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 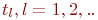
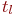
Известны вероятности перехода 

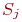
Цель моделирования: определить вероятности состояний системы после 
Обозначим эти вероятности 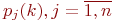

Если в системе отсутствует последействие, то есть вероятности 

Марковская цепь называется однородной, если переходные вероятности 
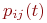
Значения 
Значения 
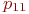
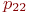
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 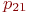
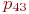
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
где 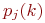
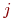

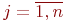
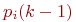
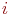

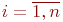
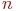

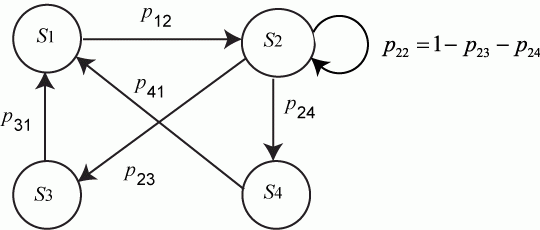
Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
где 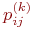

Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то — занятость. Если состояния объектов, то — поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
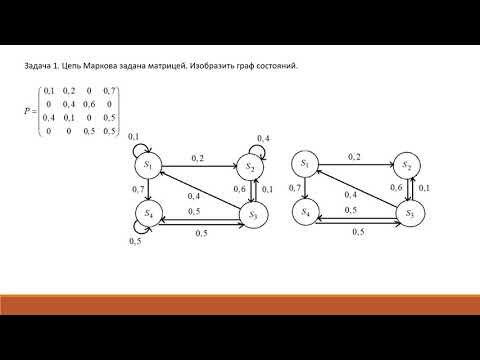
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 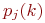
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 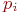

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 
где 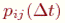


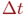
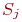
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 

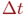
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 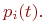
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов 
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 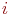
5. В правой части записывается алгебраическая сумма произведений 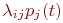
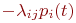
6. Определить начальные условия и решить систему дифференциальных уравнений.
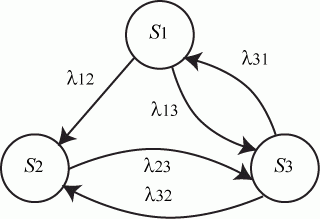
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
Рис. Размеченный граф состояний
Очевидно, 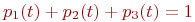
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 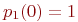
Дата добавления: 2015-04-03 ; просмотров: 7892 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Марковские процессы с дискретными состояниями. Формула Колмогорова-Чепмена.
- О решении интегрального уравнения Колмогорова-Чепмена в виде ряда Текст научной статьи по специальности « Математика»
- Аннотация научной статьи по математике, автор научной работы — Мирошин Р. Н.
- Похожие темы научных работ по математике , автор научной работы — Мирошин Р. Н.
- On the solution of the Chapman-Kolmogorov integral equation represented as a series
- Текст научной работы на тему «О решении интегрального уравнения Колмогорова-Чепмена в виде ряда»
- 🎬 Видео
Видео:уравнение колмагороваСкачать

Марковские процессы с дискретными состояниями. Формула Колмогорова-Чепмена.
Процессы с дискретным временем и дискретными состояниями называются марковскими или цепями маркова.
Процессы с дискретными состояниями; X(t) если каждое его сечение представляет собой случайную величину дискретного типа с конечным или счетным множеством состояний. Процессы с дискретными состояниями обычно изображаются в форме графов, вершины которых соответствуют возможным состояния системы, а дуги показывают непосредственные переходы из одного состояния в другое.
Основными характеристиками цепей маркова являются вероятности состояний pi(n). Вероятности того, что в момент времени tn система перешла в i-ое возможное состояние.
Предполагается, что состояния системы определены таким образом, что в каждый момент времени система находится ровно в одном из своих возможных состояний.
Для вычисления вероятности состояний вводится понятие переходных вероятностей.
Это вероятность того, что система, находящаяся в i-ом состоянии переходит в свое j- ое состояние. Pii(n) – вероятность задержки.
Если непосредственный переход из одного состояния невозможен. То переходная вероятность полагается равной 0. Если переходные вероятности зависят от номера этапа, марковская цепь называется неоднородной. В противном случае – однородной.
Pmxm=(pij) – матрица переходных вероятностей, элементы которой удовлетворяют нормировочному равенству
Граф состояний системы, дуги которого нагружены вероятностями перехода, называется размеченным графом системы.
p(0)=(p1(0),p2(0)…) компоненты которого показывают вероятности состояний системы в начальный момент времени называют вектором абсолютных вероятностей. Динамика цепи Маркова определяется вектором абсолютных вероятностей и матрицей переходных вероятностей.
Это формулы Колмогорова – Чепмена
19. Марковские процессы принятия решений с конечным числом этапов: метод итераций по стратегиям и его возможные обобщения.
Пусть имеется некоторая система S, текущее состояние которой представлено элементом из конечного множества состояний, а процесс ее функционирования и процесс принятия решения разбивается на отдельные этапы. Переходные вероятности между состояниями описываются МЦ с матрицей Рm*M=(pij). Каждый одношаговый переход сопровождается некоторым результатом rij (доходами, затратами), которые в совокупности образуют матрицу одношаговых результатов R=( rij). Величина результата определяется выбранным управлением на каждом шаге и в каждом состоянии, т.е. матрица переходных вероятностей и результатов зависит от вариантов решений, которыми располагает ЛПР. Цель — определение оптимальной стратегии, максимизирующей ожидаемый доход или минимизирующей затраты.
Хар-р задач, стоящих перед ЛПР, зависит от горизонта планирования. Если деятельность ЛПР определяется конечным числом этапов, то наиболее естественным подходом является оптимизация результата за n шагов. опр-ся вероятностными связями МЦ и выбранным управлением и называется полным ожидаемым результатом.
ЛПР может интересовать оценка полного ожидаемого результата при заранее определенной стратегии поведения в случае одного и того же состояния системы, не зависящего от № этапа. Такая стратегия называется стационарной. Если все стационарные стратегии известны, то оценив каждую из них, можно выбрать наилучший способ действия. Однако такой подход применяется преимущественно на бесконечных временных горизонтах. При конечном горизонте планирования пользуются более экономными методами, основанными на идеях динамического программирования.
Видео:03 Марковские процессы с дискретным временемСкачать
О решении интегрального уравнения Колмогорова-Чепмена в виде ряда Текст научной статьи по специальности « Математика»
Видео:Матрица интенсивностей. Система уравнений КолмогороваСкачать

Аннотация научной статьи по математике, автор научной работы — Мирошин Р. Н.
Мирошин Р.Н. О решении интегрального уравнения Колмогорова-Чепмена в виде ряда // Вестн. С.-Петерб. ун-та. Сер. 1. 2009. Вып. 2. С. 74-78. Указанное в заголовке нелинейное интегральное уравнение основное в теории случайных марковских процессов . Его решением является плотность вероятности перехода. Обычно оно решается путем сведения к линейному уравнению. В 1932 г. С. Н. Бернштейн поставил задачу его непосредственного решения. В 1962 г. О. В. Сарманов нашел такие решения в терминах билинейного ряда для стационарного Марковского процесса. В 2007 г. автор получил несколько решений в виде интегралов от произведения двух ядер известных интегральных преобразований. В этой статье без ограничений Сарманова выводятся решения в виде ряда, члены которого содержат произведение двух ортогональных функций. Результаты иллюстрируются примерами, в которых ряд суммируется к простой функции. Библиогр. 7 назв.
Видео:Цепи Маркова (видео 12) | Теория информации | ПрограммированиеСкачать

Похожие темы научных работ по математике , автор научной работы — Мирошин Р. Н.
Видео:Предельные вероятности состоянийСкачать

On the solution of the Chapman-Kolmogorov integral equation represented as a series
Miroshin R. N. On the solution of the Chapman-Kolmogorov integral equation represented as a series // Vestnik St.Petersburg University. Ser. 1. 2009. Issue 2. P. 74-78. The nonlinear integral equation, mentioned in the title, is the basic one of the theory of random Markov processes . Solution thereof is the density of transition probability function. Usually this equation is solved by means of reducing it to a linear equation. In 1932 S. N. Bernstein tackled the problem of solving it directly. In 1962 O. V. Sarmanov found such solutions for the stationary Markov process in terms of bilinear series. In 2007 the author obtained some solutions represented as integrals of the product of two kernels of known integral transformations. Free from Sarmanov restrictions, in this paper there are derived the solutions as a series, the terms of which contain the product of two orthogonal functions. The results are illustrated with examples, in which the series converges to a simple function. Bibliogr. 7 references.
Видео:Сердобольская М. Л. - Теория случайных процессов - Марковские случайные процессы (Лекция 4)Скачать

Текст научной работы на тему «О решении интегрального уравнения Колмогорова-Чепмена в виде ряда»
О РЕШЕНИИ ИНТЕГРАЛЬНОГО
УРАВНЕНИЯ КОЛМОГОРОВА—ЧЕПМЕНА В ВИДЕ РЯДА
С.-Петербургский государственный университет, д-р физ.-мат. наук, профессор, 7(812)4284285
Уравнение Колмогорова—Чепмена лежит в основе теории марковских случайных процессов. В 1932 г. С. Н. Бернштейн [1], сведя это уравнение при некоторых предположениях к дифференциальному уравнению в частных производных второго порядка параболического типа, отметил желательность непосредственного решения интегрального уравнения. Это пожелание частично реализовал О. В. Сарманов в 1961 г., найдя для стационарного процесса несколько решений в виде билинейных рядов [2]. В 2007 г. нам удалось найти решения [3], представимые однократными интегралами, используя интегральные преобразования [4]. В настоящем сообщении мы обобщаем результаты О. В. Сарманова, отказавшись от ограничительных предположений о стационарности марковского процесса и симметрии плотности распределения значений процесса относительно начального и конечного момента времени. Кроме того, мы получили решения в виде рядов, отличных от билинейных.
Рассмотрим одномерный марковский процесс с непрерывным временем t > 0 и значениями в некотором интервале Q на вещественной оси. Он характеризуется плотностью начального распределения ps(x) и плотностью вероятности перехода ns^t(x ^ у) траектории процесса из точки x в момент времени s в малую окрестность точки z в момент времени t, t > s (эта плотность может быть и обобщенной функцией). Плотность вероятности перехода удовлетворяет уравнению Колмогорова—Чепмена [5]:
ns^i(x ^ z) = ns^T(x ^ y)nT^t(y ^ z) dy , s 0. Решение уравнения (6) ищем в виде
где Б(з,Ь) > 0, а неотрицательная функция д(п) —однородная функция степени V, т. е. при к > 0
Подставив (10)—(11) в (6), находим, что Б(з,Ь) удовлетворяет функциональному уравнению
[Л(т, Ь)]1’Б(з, т) + Б(т, Ь) — Б(з, Ь) =0, з 0 — произвольная непрерывная вещественная функция, ц — вещественное
число, ^(Ь) та же, что и в (9). В силу Б(з,Ь) > 0 функция
должна быть функцией неубывающей.
некоторые частные решения уравнения Колмогорова-Чепмена (1) имеют вид
Пв^г(х ^ у) = ^2ехрип(у^А(3^)п(х), з 0. Используя (12) в (1), находим, что (1) удовлетворяется, если
аег(п) = а8т(п) ■ атг(п), з 0, / ns^t(x ^ y)dy „(ж), и„(ж) = р(ж)у>„(ж)). При этих предположениях Сарманов нашел решение уравнения (1) в виде билинейного ряда [2]
где А„ > 0 таковы, что А1 0.
«Разредив» ряд (14) путем выбрасывания из него членов с нечетными номерами п, Сарманов показал, что стационарной плотностью вероятности перехода будет и функция
ж2 + у2 — 2Джу ж2 + у2 + 2Джу
2(1 — Д2) + ехр 2(1 — Д2)
где Д = ехр(—А£), Ак = 2Ак, А > 0. Это пример (13) с /(п) = 2п. Заметим, что если в последней формуле между экспонентами поставить знак «минус» вместо знака «плюс», сузить область значений процесса до интервала П = [0, то) и зачеркнуть первую двойку в знаменателе, мы получим плотность вероятности перехода некоторого стационарного марковского процесса, но при £ > 0
и„(ж) = р(ж)Ь^(ж), «„(ж) = Ь^(ж), ^г(п) = ехр(—Ап£), где Ьа(ж) —нормированные обобщенные полиномы Лагерра [7], переходной плотностью распределения стационарного марковского процесса оказывается сумма ряда типа (13) (см. [2])
(жуе Лг)а/2р(ж) V 1 — е
в которой /а(ж) при ж > 0 — функция Бесселя.
Пример 3. Когда П = [-1,1], согласно Сарманову [2], неотрицательная функция
представима в виде ряда (13)—(14) с и„(ж) = (2п + 1)Р„(ж), «„(ж) = Р„(ж), Л„ = Ап, А > 0, р(ж) = 1/2, где Р„(ж) —ортогональные и нормированные (с весом р(ж) = 1/2) на отрезке [-1,1] полиномы Лежандра [7].
Наконец, приведем примеры не стационарных переходных плотностей, разлагаемых в ряд (13).
Пример 4. Рассмотрим гауссовский нормированный марковский процесс с нулевым средним, характеризуемый начальной плотностью распределения р(ж) = ехр(—ж2/2)/а/27г и корреляционной функцией (см. [6])
где в 0 не убывает. В этом случае пя^(ж ^ у) совпадает с правой частью (15), в которой Д определяется формулой (19). Соответственно, разложив правую часть (15) в билинейный ряд типа (13), находим, что этот ряд имеет вид (13) с /(п) = п,
П = (—оо, оо), м„(ж) = (1/а/27г) ехр(-ж2/2)Я„(ж), -у„(ж) = Я„(ж), ^(«0 = [^(¿)] ”/2-
Выбрасывая из этого ряда члены с четными номерами п, получаем плотность вероятности перехода вида (16), в которой Д определяется формулой (19), т. е. получаем пример ряда (13) с /(п) = 2п.
Аналогичным образом, выбрасывая из указанного ряда члены с нечетными номерами п, получаем плотность вероятности перехода вида (16), в которой фигурные скобки заменены знаком модуля, перед вторым слагаемым вместо знака «плюс» стоит знак «минус», а Д определяется формулой (19). Это пример ряда (13) с f (п) = 2п + 1.
Подобным же путем обобщаются и формулы (17)—(18), если в них заменить ехр(—А£) на Д(в,£) = ^(в)/^(£), в Надоели баннеры? Вы всегда можете отключить рекламу.
🎬 Видео
Цепи МарковаСкачать

Случайные процессы 9. Марковские процессы.Скачать

04 Эргодические цепи МарковаСкачать

Цепи МарковаСкачать

Лекция 13. Непрерывные марковские процессы. 30.04.2021Скачать

Соколов Д. Д. - Теория случайный процессов - Марковские цепи с непрерывным набором состоянийСкачать

Обобщенная модель марковского процессаСкачать

Решение системы уравнений Колмогорова в МатлабеСкачать

Марковские процессы 2Скачать

Шкляев А. В. - Теория случайных процессов. Семинары - Лекция 7Скачать

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Соколов Д. Д. - Теория случайный процессов - Марковские процессы с непрерывным временемСкачать

Случайные процессы 11 Непрерывные цепи МарковаСкачать

Случайные процессы 8 Марковские цепиСкачать