Уравнение бренстеда и его использование в кинетике каталитических реакций

Видео:Скорость химических реакций. 9 класс.Скачать

Уравнение Бренстеда.

Корреляционное уравнение Бренстеда связывает константы скоростей гомогенно-каталитических реакций, протекающих по механизму общего кислотного или основного катализа, с константами кислотного (К_а) или основного (К_b) равновесия тех же кислот или оснований в растворе.

Соответственно для кислот: k_НА = G (К_a) a ; (7)

Величины G_A, G_B и a, b характеризуют каталитическую реакцию и остаются постоянными только в случае кислот и оснований не отличающихся принципиально по своим свойствам (функциональные группы, ответственные за кислотные или основные свойства имеют сходное строение), а также при протекании реакции по одному и тому же механизму.

Часто уравнения (7) и (8) используют в логарифмической форме: например (7) переходит в: ln_HAk = ln G_A + a ln К_a. (9)

Отсюда легко показать, что уравнение Бренстеда соответствует принципу ЛССЭ. Действительно: ln K_а = -DF_HA/RT, где DF_HA — свободная энергия диссоциации кислоты НА. С другой стороны, логарифмируя выражение для k по теории активированного комплекса, получим: ln k_HA = -DF # _HA/RT + ln (kT/h), где DF # _HA — свободная энергия активации. Подставляя полученные выражения в (9), имеем: DF # _HA = a DF_HA + const, т.е. уравнение ЛССЭ связи свободной энергии активации реакции и свободной энергии диссоциации.

Уравнение Гаммета.

Корреляционное уравнение Гаммета связывает изменение скорости реакций при изменении природы заместителя. Один из наиболее известных примеров: зависимость константы скорости превращения мета- или пара- замещенных бензолов в реакции с одним и тем же реагентом от константы диссоциации соответствующих бензойных кислот.

Уравнение имеет вид: ln k = ln k_o + r ln 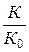, (10)

где k и k_o — константы скорости превращения замещенного и незамещенного производных бензола, K и K_о — константы диссоциации соответствующих бензойных кислот при 25 0 C в воде. Обозначив

ln 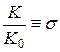, получим: lg k = lg k₀ + rs, (11)

известное в такой форме как уравнение Гаммета.

Уравнение Тафта.

Корреляционное уравнение Тафта устанавливает зависимость константы скорости превращения органических соединений от индукционного эффекта заместителя. По своей форме уравнение Тафта аналогично уравнению (11)

lg k = lg k_o + r*s*, (12)

но смысл констант здесь другой. Уравнение Тафта применимо для всех реакций, в которых на реакционную способность оказывает влияние только индукционный эффект заместителя, например, влияние заместителя на карбонильную группу при щелочном или кислотном гидролизе. Большая универсальность данного уравнения состоит и в том, что его можно расширить и учитывать влияние стерических препятствий, сопряжения и т.п. Например, для учета стерических затруднений используют уравнение:

где d — мера чувствительности реакции к cтерическим затруднениям, E_s — стерическая постоянная заместителя.

Принцип ЛССЭ широко используют для получения различных корреляционных зависимостей реакционной способности и стуктурных либо термодинамических данных. Рассмотрим несколько примеров.

1. Возьмем в качестве переменной температуру среды — Т. Тогда уравнение (4) будет иметь вид: 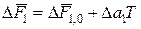(14)

Если предположить, что температура связана только с одним параметром типа х’_i, то уравнение (14) будет справедливо не только для свободных энергий, но и для любой другой характеристики

системы, зависящей от Т. Так, для объема системы при постоянном давлении V = RT/P (15)

Если в качестве стандартной температуры выбрать T = 0 K и взять V₀ = 0, то уравнения (15) и (16) эквивалентны при a_i = R/P.

2. Переменной является функциональная группа (заместитель) в одном из реагирующих соединений, характеризуемая структурным параметром x’_j, имеющим смысл количественной характеристики влияния заместителя на реакционную способность молекулы. Выражая Dа₀ = -2,303RT и учитывая, что DF_0,0 = -2,303RT lgk_0,0, где k_0,0 константа скорости или равновесия для соединений со стандартным заместителем, получим:

Под величиной c следует понимать обобщенную постоянную, характеризующую заместитель. Подставляя (17) в (6) и обозначив B ≡ j, получаем для любой реакционной серии:

где lg k_i,0 = A¢ — B lg k_0,0 и j_i — обобщенная постоянная, характеризующая реакционную серию (тип реакции). Уравнения (11) и (12) являются частным случаем уравнения (18).

3. Переменным фактором является одно из реагирующих веществ. Если при изменении этого реагента меняется лишь одно свойство системы, то по аналогии с предыдущим напишем:

где k_i — константа скорости при взаимодействии с данным реагентом, k_i,0 — тo же для стандартного реагента для данного типа реакции, q — постоянная, характеризующая данное реагирующее соединение и p_i — постоянная, характеризующая данный тип реакции (реакционную серию). Частным случаем (19) является уравнение Бренстеда (7). Покажем это следующим образом. Представим (7) в виде:

(20)

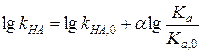
Отсюда следует, что a = p_i и q = 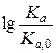. НА при этом соответствует стандартной кислоте.

Аналогично можно рассмотреть как переменные факторы природу растворителя, давление и т.п.

Видео:Химическая кинетика. Формальная кинетика простых гомогенных реакций в закрытых системахСкачать

Уравнение Бренстеда

Вы будете перенаправлены на Автор24

Видео:Химическая кинетика. Скорость химической реакции | ХимияСкачать

Катализатор и его каталитическая активность

Одним из важнейших вопросов катализа является проблема взаимосвязи электронного строения катализатора с его каталитической активностью.

В кислотно — основном катализе параметром, отражающим электронное строение, выступает величина $pK_a$ катализатора.

Бренстед и Педерсен вывели соотношение, показывающее связь между катализатором и катализируемыми им реакциями на примере разложения нитрамида:

Для данной реакции характерна линейная корреляция между логарифмом константы скорости и величиной $pK_a$ основания. И нитрамид и все рассмотренные Бренстедом основания были «жесткими». Поэтому вероятность нахождения протона в переходном состоянии ближе к основанию, чем к кислоте, маловероятна.

Бренстед установил, что чем сильнее основание (или кислота), тем оно эффективнее как общий основной (кислотный) катализатор.

Каталитический закон Бренстеда можно представить через:

константу скорости реакции кислоты

где индексы $A$ и $alpha $ характеризуют кислоту, а $G$ — константа.

константу скорости реакции основания

где индексы В и $beta $ характеризуют основание, а $K_a$— константа диссоциации кислоты $A$ или кислоты, сопряженной с основанием $B$.

Полученные уравнения можно представить в линейной логарифмической форме:

где $k_A$ и $k_B$ —константы скорости реакций, катализируемых кислотами и основаниями;

$K_a(AH)$ и $K_a(BH^+)$ — константы диссоциации катализаторов;

$alpha $ и $beta $ — коэффициенты Бренстеда.

Зависимость $logk_A$ от $pK_a$ — линейная с наклоном — $alpha $; зависимость $logk_B$ от $pK_a$ — линейная с наклоном + $beta $.

Катализ реакции разложения нитрамида (Рис. 1). На графике можно наблюдать хорошую линейную корреляцию на протяжении трех единиц $pK$, а также около двух десятичных порядков по константе скорости. Наклон прямой линии $beta $ равен $0,66.$

Рисунок 1. Катализ реакции разложения нитрамида

Если общие кислоты или основания содержат более одной ионизируемой группы, то константы ионизации испытывают взаимное влечение. Для анализа таких реакций вводят статистические поправки.

Готовые работы на аналогичную тему

Видео:Теории кислот, оснований и растворов. Теория Брёнстеда-Лоури. 11 класс.Скачать

Линейные соотношения Бренстеда

Линейные соотношения Бренстеда справедливы для каталитических реакций, которые протекают если:

• в качестве реагентов или катализаторов выступают кислород- или азотсодержащие кислоты или основания;
• значения констант скоростей меньше, чем диффузионный предел.

Случаи нарушения линейности и другие отклонения от соотношения Бренстеда:

• в качестве реагентов или катализаторов выступают карбокислоты или карбоснования;
• константы скорости близки к диффузионному пределу;
• если структурные изменения в молекуле или сольватной оболочке влияют на кинетику протонного переноса;
• если реакции катализируются первичными, вторичными, третичными аминами (причины: пространственная деформация, различия в сольватации, специфические сольватационные эффекты, стерические затруднения в молекуле субстрата или катализатора, изменение механизма реакции).

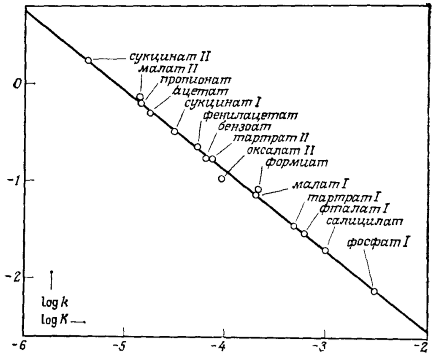
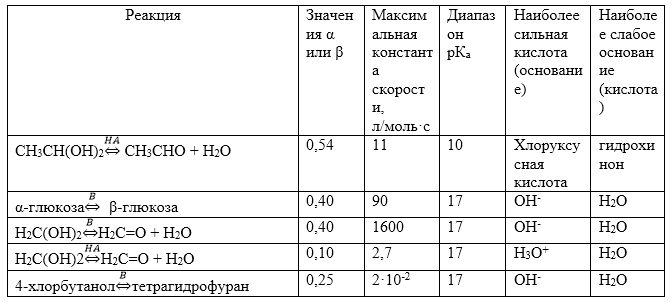
Примеры реакций, подчиняющихся закону Бренстеда, приведены в табл.1.

Рисунок 2. Некоторые линейные соотношения Бренстеда

Видео:СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ. КАТАЛИЗАТОР.Скачать

Смысл каталитического уравнения Бренстеда

Бренстед предположил существование взаимосвязи между константой скорости реакции и константой равновесия лимитирующей стадии переноса протона.

Для общего основного катализа уравнение Бренстеда имеет вид:

Если прологарифмировать уравнение

Так как последние три члена постоянны, уравнение можно представить в виде

Между логарифмами константы скоростей и константы равновесия существует линейная зависимость для простых систем.

Для объяснения уравнения Бренстеда используют диаграммы молекулярной потенциальной энергии.

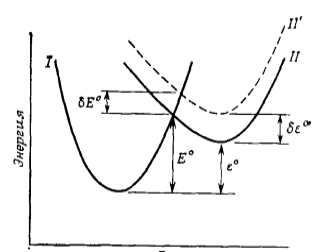
Если допустить, что перенос протона — это трехцентровая реакция, вклад в энергию отталкивания вносит только взаимное влияние двух тяжелых атомов, которые неподвижны и отстоят друг от друга на фиксированном расстоянии, при этом протон перемещается между ними, то такую реакцию можно описать профилем потенциальной энергии (Рис. 3).

На диаграмме не отображены энергия отталкивания и резонансное взаимодействие, снижающее энергию переходного состояния.

Рисунок 3. Профиль потенциальной энергии вдоль координаты реакции, иллюстрирующий молекулярную основу уравнения Бренстеда

Кривая $І$ описывает систему исходных веществ $SH + B$, где $SH$ — субстрат, $B$ — катализатор (основание).

Кривая $ІІ$ описывает систему $S^- + BH^+$. При этом энергия активации равна $Е^º$, а изменение свободной энергии в ходе реакции $varepsilon^º$. Если в молекулу катализатора ввести заместитель, вызывающий уменьшение основных свойств, то кривая $ІІ$ переместится в положение $ІІ`$. Кривая $ІІ`$ будет смещена по оси энергии вверх.

Приращение $delta $Е и $delta varepsilon^º$ связаны соотношением

где $S1$ и $S2$- наклоны двух прямых в точке пересечения.

Данное уравнение отображает каталитический закон Бренстеда.

Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

УРАВНЕНИЕ БРЁНСТЕДА—БЬЕРРУМА

Пусть речь идет о реакции в растворе между ионами В и С с зарядами Zb и Zq. Предположим, что реакция медленная. Тогда концентрацию пар столкновения В-С можно принять приблизительно равновесной, соответствующей термодинамической константе равновесия на основе концентрации:

где с е — стандартная концентрация, делающая активности безразмерными (обычно с е = 1 моль • дм -3 ); у, — коэффициенты активности на основе концентрации.

Из этого следует:

Подставив это выражение в (15.2), получим: где величина

представляет собой наблюдаемый коэффициент скорости реакции при химическом контроле. Ранее он обозначался k_R, однако результат, который выводится ниже, верен для реакций как с химическим контролем, так и с диффузионным (хотя вывод для общего случая очень сложен). Поэтому индекс R будет опущен.

В бесконечно разбавленном растворе коэффициенты активности растворенных веществ равны 1. Поэтому (15.12) можно записать также в виде:

где к°° — коэффициент скорости в бесконечно разбавленном растворе, к°° = k₂Kf /с е .

Применим теперь предельное уравнение Дебая—Хюккеля для индивидуальных ионов, следующее из (8.20) при ионной силе, стремящейся к нулю:

Применение к логарифму отношения к_к/ /с^ из (15.13) дает:

Здесь принято во внимание, что зарядовое число пары столкновения г_в. _с равно сумме зарядовых чисел ионов В и С.

Таким образом, получилось уравнение зависимости коэффициента скорости от ионной силы:

Его называют уравнением Брёнстеда—Бьеррума.

Следует заметить, что параметр А из теории Дебая—Хюккеля имеет здесь величину и размерность, соответствующие ионной силе на основе концентрации. Для воды при 25°С он равен 1,176 (дм 3 — моль -1 ) 1/2 . Но уравнение Брёнстеда—Бьеррума часто записывают через десятичный логарифм с тем же обозначением коэффициента А. В такой записи он меньше в 1п( 10) раз, т.е. составляет 0,511 (дм 3 • моль _1 ) 1/2 . Таким образом, для воды при 25°С и обычном давлении:

Уравнение Брёнстеда—Бьеррума показывает, что логарифм коэффициента скорости к является линейной функцией корня квадратного из ионной силы в сильно разбавленных растворах, причем наклон этой зависимости зависит от произведения зарядовых чисел реагирующих ионов. Если реагируют ионы с одинаковыми знаками зарядов, то > 0 и к увеличивается с увеличением /_с. Если реагируют противоположно заряженные ионы, то — и для гидролиза сахарозы под действием ионов Н + . Объяснение этой слабой зависимости заключается в том, что ионная сила влияет не только на энергию взаимодействия между заряженными частицами, но и на энергию электростатического взаимодействия иона с полярной (или поляризованной) молекулой. Уравнение Брёнстеда—Бьеррума не учитывает этого вида взаимодействия.

В истории химической кинетики некоторое время предполагалось, что скорость реакции в неидеальном растворе должна быть пропорциональна активностям участников реакции, а не концентрациям. В связи с уравнением Брёнстеда—Бьеррума можно убедиться, что это предположение неверно. Для этого сравним уравнения скорости одной и той же реакции ионов В и С:

где к°°’ — константа скорости в идеальном разбавленном растворе (константа скорости нулевого порядка, так как активности безразмерны); к°° — аналогичная константа скорости с обычной размерностью: Г = к°°’/(с е ) 2 .

Приравняем правые части этих уравнений и получим: к = к°°у_су_в. Возьмем логарифм и применим уравнение Дебая—Хюккеля:

Как видно, это уравнение отличается от уравнения Брёнстеда— Бьеррума. По нему влияние ионной силы на константу скорости не зависит от знаков зарядов ионов В и С, а зависит только от их абсолютных величин. Это противоречит экспериментальным данным.

Уравнение Брёнстеда—Бьеррума часто применяют для определения зарядового числа одного из участников реакции, когда зарядовые числа других участников известны. Для этого просто находят произведение зарядовых чисел из коэффициента наклона экспериментальной зависимости логарифма коэффициента скорости от корня квадратного из ионной силы. Важно заметить, однако, что этим методом невозможно определить, каков именно механизм реакции.

Выше подразумевалось, что речь идет о бимолекулярной реакции ионов В и С в клетке. Но если реакция В и С сложная, то из солевого эффекта нельзя определить, через какие стадии она проходит. Классический пример этого — реакция получения мочевины из цианата аммония. Коэффициенты скорости в двух уравнениях скорости:

обе константы скорости зависят от ионной силы в согласии с уравнением Брёнстеда—Бьеррума для соответствующих реакций:

и

Это объясняется тем, что коэффициенты к_< и к₂ связаны между собой через константы равновесий диссоциации циановой кислоты и аммоний-иона. Из-за этого солевой эффект не позволяет определить, какая из этих двух реакций происходит на самом деле.

Таким образом, солевой эффект является свойством коэффициента к в эмпирическом уравнении скорости реакции, а не свойством молекулярного механизма. Уравнение Брёнстеда—Бьеррума (15.15) — уравнение для коэффициента скорости реакции второго порядка, справедливое независимо от того, какой она является — элементарной или нет.

🎬 Видео

Кинетический анализ сложных реакцийСкачать

Катализ. 10 класс.Скачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Лекция 8. «Формальная кинетика сложных реакций»Скачать

Определение порядка реакции методом подбора кинетического уравненияСкачать

Химия для чайников. Лекция 11. Кинетика химических реакций. Захватывает дух от скоростиСкачать

ФЕРМЕНТЫ 5.Основы ферментативного катализа. Кинетика ферментативных реакций.Скачать

Этапы ферментативного катализа. Взаимодействие ферментов с несколькими субстратамиСкачать

Лекция 12. «Кинетика реакций с участием твердых веществ. Гетерогенный катализ»Скачать

Теория Бренстеда-Лоури (видео 2) | Кислоты и Основания | ХимияСкачать

Лекция 28.10.20 | Параллельные реакции, катализ, схема Михаэлиса-Ментен | Химическая кинетикаСкачать

Лекция 18.11.20 | Гетерогенный катализ (завершение), уравнение Аррениуса | Химическая кинетикаСкачать

Введение в кинетикуСкачать

5 6 КатализСкачать