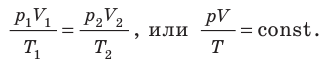Закон Бойля-Мариотта — один из основных газовых законов, он описывает изотермические процессы в газе.
Процесс изменения состояния термодинамической системы при постоянной температуре называется изотермическим. Закон Бойля-Мариотта гласит:
Для данной массы произведение давления газа на его объем постоянно, если температура газа не меняется.
Этот закон был экспериментально открыт английским ученым Р. Бойлем в 1662 г., в 1676 г. его сформулировал также французский ученый Э. Мариотт.
Закон строго выполняется только для идеальных газов. Для реальных газов он выполняется достаточно хорошо при небольших давлениях и высоких температурах. Так, при давлении 100 атм и температуре 0 °С отклонение измеренного значения pV от расчетного составляет 7%. Закон Бойля-Мариотта, как и другие газовые законы, является следствием уравнения состояния идеального газа.
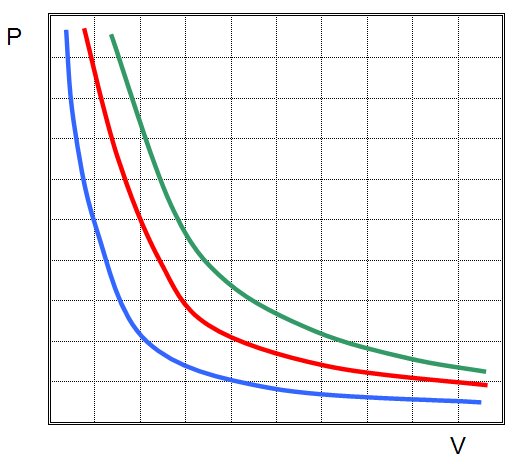
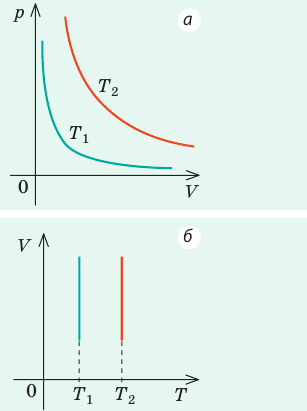
Графики зависимости p(V) при Т = const (р = const/V) называются изотермами и представляют собой равносторонние гиперболы (площади S1 = S2). Чем выше температура, тем выше лежит соответствующая ей изотерма
- Идеальный газ и уравнение Бойля-Мариотта. Пример задачи
- Что понимают под идеальным газом?
- Уравнение Бойля-Мариотта
- Уравнение состояния газа идеального
- Другие законы газовые
- Пример задачи на применение Бойля-Мариотта закона
- Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- 💡 Видео
Видео:Решение задач по теме: закон Бойля-МариоттаСкачать
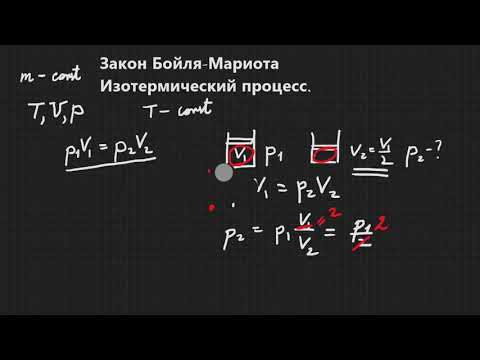
Идеальный газ и уравнение Бойля-Мариотта. Пример задачи
Изучение свойств идеального газа является важной темой в физике. Знакомство с характеристиками газовых систем начинают с рассмотрения уравнения Бойля-Мариотта, поскольку оно является первым экспериментально обнаруженным законом идеального газа. Рассмотрим его подробнее в статье.
Видео:Основы молекулярной физики | закон Бойля МариоттаСкачать
Что понимают под идеальным газом?
Прежде чем говорить о законе Бойля-Мариотта и уравнении, которое его описывает, дадим определение идеальному газу. Под ним принято понимать текучую субстанцию, в которой составляющие ее частицы друг с другом не взаимодействуют, и их размеры пренебрежимо малы в сравнении со средними межчастичными расстояниями.
В действительности любой газ является реальным, то есть составляющие его атомы и молекулы имеют определенный размер и между собой с помощью Ван-дер-ваальсовых сил не взаимодействуют. Однако, при высоких абсолютных температурах (больше 300 К) и низких давлениях (меньше одной атмосферы) энергия кинетическая атомов и молекул намного превышает энергию Ван-дер-ваальсовых взаимодействий, поэтому реальный газ при указанных условиях с высокой точностью может считаться идеальным.
Видео:Газовые законыСкачать

Уравнение Бойля-Мариотта
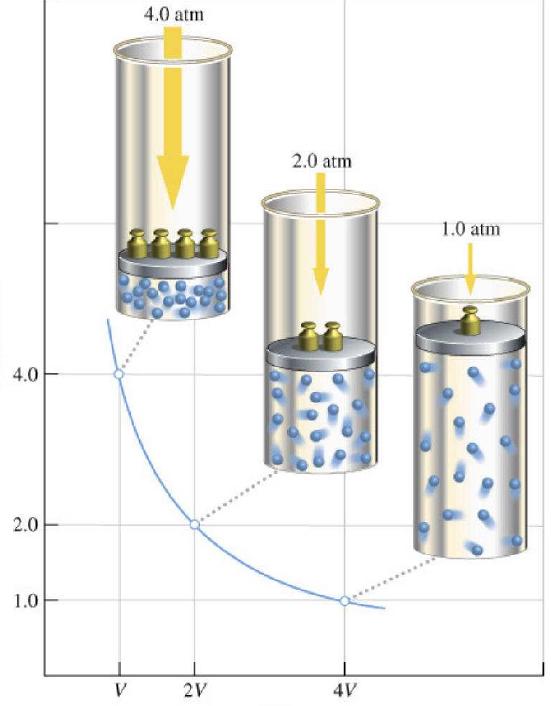
Свойства газов европейские ученые активно исследовали в течение XVII-XIX веков. Самым первым газовым законом, который был открыт экспериментально, стал закон, описывающий изотермические процессы расширения и сжатия газовой системы. Соответствующие опыты были проведены Робертом Бойлем в 1662 году и Эдмом Мариоттом в 1676 году. Каждый из этих ученых независимо показал, что во время изотермического процесса в закрытой газовой системе изменяется давление объему обратно пропорционально. Полученное экспериментально математическое выражение процесса записывается в следующем виде:
Где P и V — давление в системе и ее объем, k — некоторая постоянная, значение которой от количества вещества газа и от его температуры зависит. Если построить зависимость функции P(V) на графике, то она будет представлять собой гиперболу. Пример этих кривых показан ниже.
Записанное равенство называется уравнением (законом) Бойля-Мариотта. Этот закон кратко можно сформулировать так: расширение идеального газа при постоянной температуре приводит к пропорциональному уменьшению давления в нем, наоборот, изотермическое сжатие газовой системы сопровождается пропорциональным повышением давления в ней.
Видео:ЛР-10-2-01 Проверка закона Бойля-МариоттаСкачать

Уравнение состояния газа идеального
Бойля-Мариотта закон частным случаем является более общего закона, который носит фамилии Менделеева и Клапейрона. Эмиль Клапейрон, обобщая экспериментальную информацию поведения газов при различных внешних условиях, в 1834 году получил следующее уравнение:
Иными словами, произведение объема V газовой системы на давление P в ней прямо пропорционально произведению абсолютной температуры T на количество вещества n. Коэффициент этой пропорциональности обозначен буквой R и называется газовой универсальной постоянной. В записанном уравнении величина R появилась благодаря замене ряда констант, которую сделал Дмитрий Иванович Менделеев в 1874 году.
Из универсального уравнения состояния легко увидеть, что постоянство температуры и количества вещества гарантирует неизменность правой части равенства, а значит, левая часть равенства также будет оставаться постоянной. В таком случае мы получаем уравнение Бойля-Мариотта.
Видео:Физика для чайников. Урок 26. Закон Бойля-МариоттаСкачать

Другие законы газовые
Записанное в пункте выше Клапейрона-Менделеева уравнение содержит три термодинамических параметра: P, V и T. Если каждый из них фиксировать, а двум остальным позволять меняться, то мы получим уравнения Бойля-Мариотта, Шарля и Гей-Люссака. Шарля закон говорит о прямой пропорциональности между объемом и температурой для изобарного процесса, а Гей-Люссака закон утверждает, что в случае изохорного перехода давление газа растет или уменьшается абсолютной температуре прямо пропорционально. Соответствующие уравнения выглядят так:
P/T = const при V = const.
Таким образом, Бойля-Мариотта закон является одним из трех основных газовых законов. Тем не менее он отличается от остальных в плане графической зависимости: функции V(T) и P(T) являются прямыми линиями, функция P(V) — это гипербола.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Пример задачи на применение Бойля-Мариотта закона
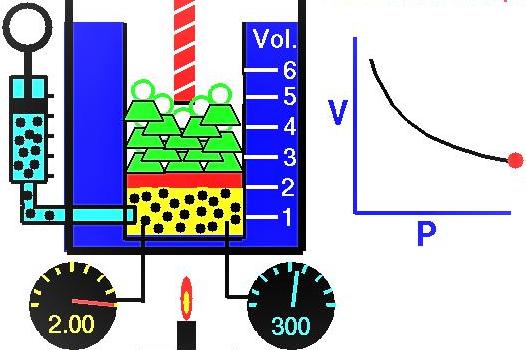
Объем газа в цилиндре под поршнем в начальном положении составлял 2 литра, и его давление было равно 1 атмосфера. Чему стало равно давление газа, после того как поршень поднялся, и объем газовой системы увеличился на 0,5 литра. Процесс считать изотермическим.
Поскольку нам даны давление и объем идеального газа, а также известно, что температура в процессе его расширения остается неизменной, то мы вправе воспользоваться уравнением Бойля-Мариотта в следующей форме:
Это равенство говорит о том, что произведение на объем давления является постоянным для каждого состояния газа при данной температуре. Выражая из равенства величину P2, получаем конечную формулу:
При выполнении вычислений давления можно использовать внесистемные единицы в данном случае, поскольку литры сократятся, и мы получим давление P2 в атмосферах. Подставив данные из условия, приходим к ответу на вопрос задачи: P2 = 0,8 атмосферы.
Видео:закон бойля мариоттаСкачать

Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Видео:Рассмотрение темы: "Изотермический процесс. Закон Бойля-Мариотта" (полное видео)Скачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 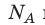
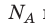
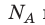
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
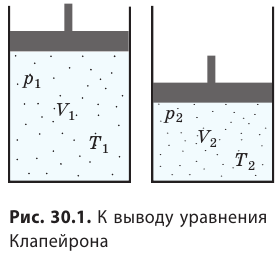
Уравнение Клапейрона
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (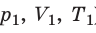
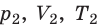
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 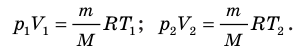
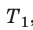
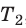
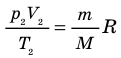
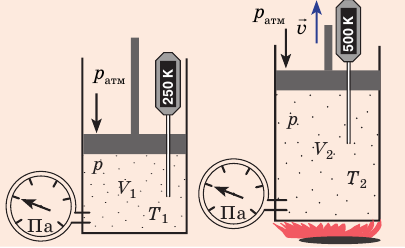
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (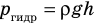
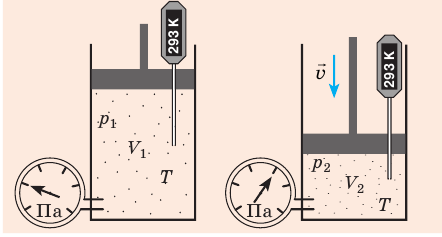
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (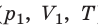
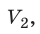
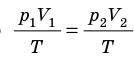
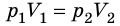
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 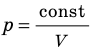
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (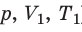
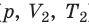
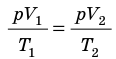
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
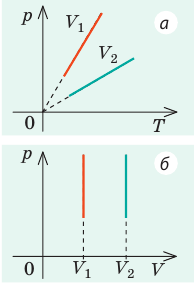
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (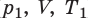
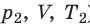
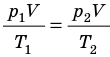
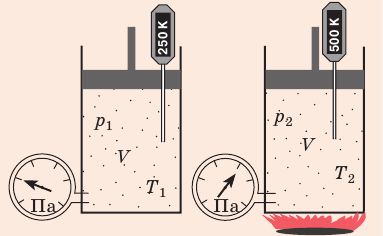
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 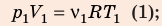
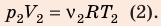

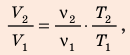
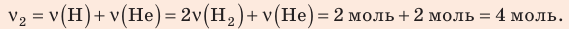
Ответ: примерно в 2,7 раза.
Пример №2
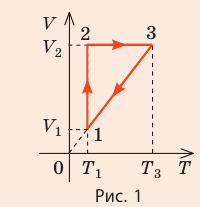
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
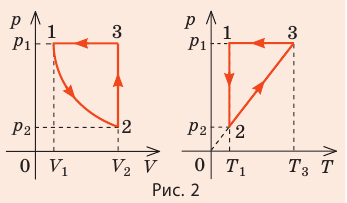
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💡 Видео
Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

Уравнения и графики Изотермического Процесса.Закон Бойля-Мариотта.Каргту.Ис19-3Скачать

мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

Опыт. Проверка закон Бойля-МариоттаСкачать

Физика - Газовые законы. Уравнение идеального газа.Скачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

§ 22 Закон Бойля-Мариотта. Изотермический процессСкачать

Законы идеального газа. Видеоурок 29. Физика 10 классСкачать

Физика для чайников. Лекция 26. Закон Бойля - МариоттаСкачать

Объединенный газовый закон. Видеоурок 30. Физика 10 классСкачать

Физика # 26. Закон Бойля-МариоттаСкачать


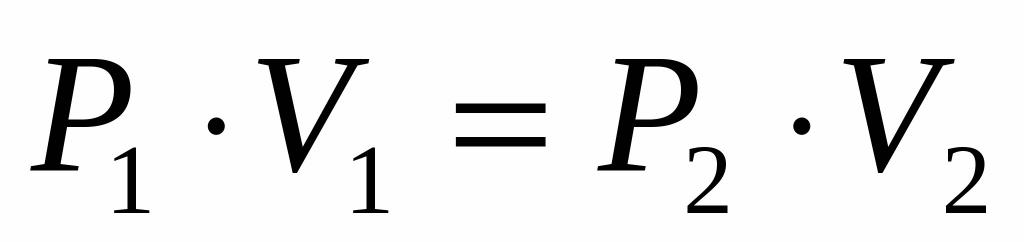
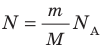
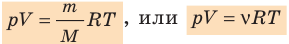
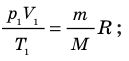
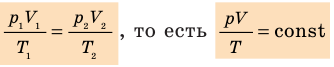
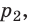
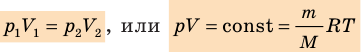

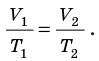
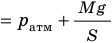
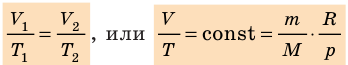
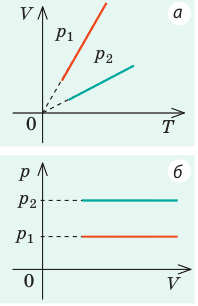

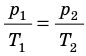
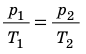
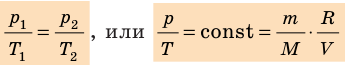

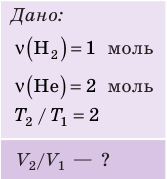
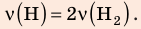

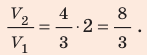
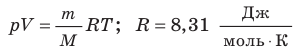 — универсальная газовая постоянная.
— универсальная газовая постоянная.