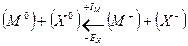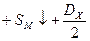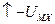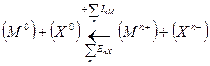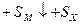Уравнение борна ланде и константа маделунга

Видео:Урок 57. Уравнение Борна-Ланде. Типы решеток вида ХУ.Скачать

Уравнение борна ланде и константа маделунга

В ионных кристаллах электроны переходят от атомов одного типа к атомам другого, так что кристалл состоит из положительных и отрицательных ионов. Для того чтобы с помощью сил электростатического притяжения между валентными электронами и ионными остовами образовать из атомов твердые тела, необходимо выполнить следующие четыре условия [63]:

1. Положительно заряженные ионные остовы должны находиться на таком расстоянии друг от друга, чтобы при этом было сведено до минимума кулоновское отталкивание между ними.

2. Валентные электроны должны находиться на определенных расстояниях друг от друга, отвечающих тому же требованию.

3. Одновременно со вторым условием валентные электроны должны быть настолько близко расположены от положительных ионов, чтобы кулоновское притяжение между разноименными зарядами было максимально.

4. При выполнении всех этих условий потенциальная энергия системы может уменьшиться, однако это должно происходить таким образом, чтобы кинетическая энергия системы лишь немного возросла.

В ионных кристаллах ионы располагаются так, что кулоновское притяжение между разноименно заряженными ионами сильнее, чем кулоновское отталкивание между ионами одного знака заряда. Таким образом, ионная связь – это связь, обусловленная в основном электростатическим взаимодействием противоположно заряженных ионов [74].

Наиболее характерные ионные кристаллы – NaCl , CsCl (галогениды щелочных металлов).

Как было указано выше, тип связи между атомами во многом определяется степенью ионизации в соединении. Степень ионизации атомов, составляющих ионный кристалл, часто такова, что электронные оболочки всех ионов соответствуют электронным оболочкам, характерным для атомов инертных газов. Например, нейтральные атомы лития и фтора имеют следующую структуру электронной оболочки Li − 1 s 2 2 s , F − 1 s 2 2 s 2 2 p 5 . В кристалле фтористого лития электронная конфигурация у однократно заряженных ионов становится: Li + − 1 s 2 , F — − 1 s 2 2 s 2 2 p 6 . Такая конфигурация характерна для атомов гелия и неона. Атомы инертных газов имеют замкнутые электронные оболочки, и распределение заряда в них имеет сферическую симметрию. Поэтому можно ожидать, что распределение заряда каждого иона в ионном кристалле приближенно обладает сферической симметрией, которая несколько нарушается в области соприкосновения соседних атомов.

На больших расстояниях взаимодействие между ионами с зарядами + q и — q представляет собой кулоновское притяжение зарядов противоположного знака и кулоновское отталкивание ионов одного знака с потенциалом . При образовании устойчивой кристаллической структуры основной вклад в энергию связи дает электростатическая энергия, которую называют энергией Маделунга . Энергию взаимодействия i-й частицы со всеми остальными частицами, составляющими кристалл, можно рассчитать по формуле (2.13). Предположим, что в формуле (2.13) может быть представлено в виде суммы двух потенциалов: потенциала сил отталкивания некоторого центрального поля, изменяющегося по закону Борна−Майера (2.9), и кулоновского потенциала . Тогда

.

В формуле (2.15) знак (+) используется в случае одинаковых по знаку зарядов, а знак (–) соответствует разноименным зарядам.

Введем величину , определяемую соотношением , где R – расстояние между соседними ионами в кристалле. Если мы будем учитывать отталкивание только ближайших соседей, то получим

для ближайших соседей

для прочих пар атомов.

Таким образом, согласно равенству (2.14), полная энергия:

,

где Z – число ближайших соседей какого-либо иона, N – число ионных пар, а через a обозначена постоянная Маделунга

.

Формулу (2.18) можно переписать в виде:

,

где – расстояние иона с номером j от исходного.

Полную энергию кристаллической решетки, состоящей из 2 N ионов и находящейся в состоянии равновесия, учитывая, что , можно записать в виде:

,

где – равновесное расстояние между ионами. Выражение (2.20) называется формулой Борна−Майера .

Величина − энергия Маделунга . Постоянная r имеет размерность длины и приблизительно равна .

Покажем пример расчета постоянной Маделунга на бесконечной цепочке ионов противоположных знаков. Выберем отрицательный заряд как начальный. Обозначим R – расстояние между ионами, тогда

или иначе .

Множитель 2 перед скобками появляется из-за соседства ионов одного знака слева и справа от исходного. Применим разложение в ряд , тогда x =1 и указанный ряд для a сходится к значению .

Наряду с формулой Борна−Майера (2.20), для расчета энергии сцепления ионного кристалла часто используется формула Борна−Ланде :

.

Здесь и − заряды взаимодействующих ионов, n − постоянная, представляющая собой показатель степени в формуле (2.8), − равновесное расстояние между ионами.

Если известны заряды ионов и структура кристалла (из них можно рассчитать постоянную Маделунга ), то для вычисления энергии сцепления нужно знать еще показатель степени в потенциале сил отталкивания n . Его обычно определяют из сжимаемости кристалла æ. По определению,

,

где V − объем кристалла, p − давление. При температуре 0K , т. е.

.

Объем кристалла можно определить из соотношения , где N − число пар ионов, g − множитель, значение которого зависит от типа структуры. Так, для структуры NaCl объем, занимаемый N молекулами, равен , где − расстояние между ближайшими ионами ( − радиус аниона, − радиус катиона), . Для CsCl множитель ; для ZnS со структурой вюрцита и т. д. Используя приближение Борна — Ланде, получим

.

Множитель появился при записи кулоновского потенциала притяжения в виде в системе СИ: .

Подставляя в (2.24) , , , м, Кл, для NaCl , получим и полную потенциальную энергию, приходящуюся на пару ионов, . Это значение хорошо согласуется с полученным экспериментально при комнатной температуре, которое составило [63].

Формула Борна−Ланде не является чисто теоретической, т. к. величины n , необходимые для расчета, определяются из экспериментально найденной величины сжимаемости. При этом расхождение теоретических и расчетных данных может доходить до 3 %.

Оценим, пользуясь формулой Борна−Майера (2.20), величину r , имеющую физический смысл размера области, где проявляется взаимодействие отталкивания.

.

Если в формулу (2.25) подставить данные для кристалла NaCl , то получим . Отсюда следует, что взаимодействие отталкивания проявляется в области размером м .

Видео:Ионная связь (химическая связь, часть 4)Скачать

Константы Маделунга некоторых структурных типов

Величина А получается в результате суммирования бесконечного ряда, заключенного в скобки, зависит от геометрического типа структуры, но не зависит от межатомных расстояний. Она называется постоянной Маделунга, в честь ученого, который впервые рассчитал эти суммы. Для кристаллов со структурой хлорида натрия она равна 1,7476.

Чтобы найти энергию всей решетки нужно величину кулоновского взаимодействия j умножить на число ионов в молекуле (формульной единице, для NaCl — 2) и число Авогадро и разделить на 2, поскольку каждое парное взаимодействие относится к двум ионам, получим:

В этом выражении для краткости обычно опускают постоянный множитель Ne 2 . Значение энергии, вычисленное по приведенной формуле, правильно только при допущении, что ионы – твердые недеформируемые шары, кратчайшее расстоянии между которыми не может быть меньше R. Однако твердые тела сжимаемы, и ионы деформируются. По мере увеличения сжатия сопротивление кристалла растет. Ионы отталкиваются друг от друга, силы отталкивания возрастают по мере сближения ионов друг с другом. В 1918 году М. Борн и его сотрудники предложили две формулы для потенциала отталкивания: степенную , и экспоненциальную . Параметры b и n, В и r определяются на основании экспериментальных данных по сжимаемости кристалла.

В состоянии равновесия энергия решетки равна:

и

Энергия решетки должна быть минимальна, то есть при равновесном межатомном расстоянии R₀ должно выполняться условие:

Это означает равенство сил притяжения и отталкивания:

и

Отсюда выразим b и В, подставим их в уравнение для энергии решетки и получим:

— уравнение Борна – Ланде.

— уравнение Борна – Майера.

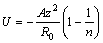
Параметры n и r определяются из данных о сжимаемости кристалла, среднее значение n близко к 9 (от 5 до 12) и зависит от типа оболочки ионов. Для кристаллов, состоящих из разных ионов, берут среднее значение n. среднее значение r оказалось более постоянным и составляет 0,35 ± 0,05 A.

Экспериментально определить величину энергии кристаллической решетки позволяет процесс известный как цикл Борна — Габера. В общем виде для кристалла ионного кристалла М_xA_y энергия кристаллической решетки определяется как: ,

где DН_ат – энергия образования атомов из элементов в стандартных состояниях; m = x + y – число атомов в соединении; — сумма потенциалов ионизации всех катионов; — сумма значений сродства к электрону всех анионов.

Расчет энергии кристаллической решетки хлорида натрия
Согласно круговому процессу ионный кристалл NaCl, можно получить двумя различными способами:

● прямым взаимодействием металлического натрия и газообразного хлора, при котором выделяется энергия (-Q), соответствующая энтальпии образования DНf ;

● переход от тех же состояний элементов к кристаллу через газовую фазу. В начале металл натрий переходит в одноатомный пар, для чего затрачивается энергия сублимации S; одновременно молекулы Cl2 диссоциируют на атомы, на этот процесс затрачивается энергия 1/2D. Далее атом натрия отдает один электрон и переходит в ион Na+ (энергия процесса равна потенциалу ионизации I). Атом хлора присоединяет этот электрон и образует ион Cl- (энергия процесса равна сродству к электрону Е). Ионы в газовой фазе взаимодействуют, образуя кристалл с выигрышем энергии решетки U.

Оба способа приводят к одному результату, по закону Гесса энергетические эффекты должны быть одинаковы: DНf = S + 1/2D + I – E + U

отсюда получим: U = DНf — S — 1/2D — I + E

Ковалентные кристаллы

Ковалентная химическая связь – и это связь, которая возникает между атомами за счет образования общих электронных пар.

Ковалентная связь существует между атомами, как в молекулах, так и в кристаллах. Она возникает как между одинаковыми атомами (например, H₂, Cl₂), так и между разными атомами (например, H₂O, NH₃, HCl). Почти все связи в органических соединениях – ковалентные.

Насыщаемость – одно и важнейших свойств ковалентной химической связи. Вследствие насыщаемости связи молекулы имеют определенный состав и существуют в виде дискретных частиц с определенной структурой. Каждая пара атомов в молекуле удерживается вместе при помощи одной или нескольких общих электронных пар, таким образом, связь локализована между двумя атомами, то есть она двухцентровая и двухэлектронная. Количество связей ограничено числом валентных электронов и числом валентных орбиталей, поэтому связь насыщенна.

Направленность ковалентной связи связана с направленностью электронных облаков. Электронные облака имеют различную форму, и их взаимное перекрывание может осуществляться различными способами. В зависимости от способа перекрывания и симметрии образующегося облака различают -, -, -связи.

В гомоядерных двухатомных молекулах одна или несколько электронных пар в равной мере принадлежит обоим атомам. При образовании молекул H₂, Cl₂, F₂ и др. каждое ядро атома с одинаковой силой притягивает пару связывающих электронов. Такая связь называется неполярной ковалентной связью:

Если взаимодействующие атомы характеризуются различными значениями электроотрицательности, то обобществленная пара электронов смещается к более электроотрицательному атому. Такая связь называется ковалентной полярной связью:

Вследствие смещения пары электронов от одного атома к другому, средняя плотность отрицательного заряда у одного из атомов будет выше, чем у другого. Поэтому один из атомов приобретает избыточный положительный, а другой избыточный отрицательный заряд. Эти заряды называются эффективными зарядами атомов:

+0,17 H Cl -0,17

Кристаллические вещества с ковалентным типом химической связи характеризуют диэлектрические или полупроводниковые свойства, средние значения твердости и плотности, низкая тепло- и электропроводность.

Энергия сцепления атомов, связанных ковалентно, измеряется в процессе диссоциации молекулы или сублимации кристалла с образованием одноатомного газа. Поэтому энергию сцепления ковалентного кристалла можно назвать энергией атомизации, чтобы отличить её от энергии ионной решетки, которая выделяется при образовании кристалла из газа ионов.

Расчет энергии ковалентного кристалла очень сложен, так как необходимо решение многих квантовомеханических задач. Поэтому до сих пор главными способами оценки ковалентной связи являются эмпирические методы. Опыт показывает, что равновесная энергия одинарной гомополярной связи находится в довольно простой линейной зависимости от её длины. Зависимость выражается приближенным уравнением:

Е (ккал) = — 38 R ( 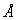) + 136

Изменение энергии отдельной связи при изменении межатомного расстояния DR обычно передается с помощью функции Морзе:

,

где D – энергия диссоциации (D₀ = —E₀), , где k – силовая константа связи, которая в свою очередь обратно пропорциональна квадрату длины связи: .

Молекулярные кристаллы

В молекулярных кристаллах существуют силы дополнительного взаимодействия между атомами, которые называют Ван-дер-ваальсовыми силами или остаточной связью. Кристаллами с такой связью являются водород, кислород, азот и молекулярные кристаллы большинства органических соединений. Именно остаточная связь, действующая между молекулами, обеспечивает существование таких кристаллов. Остаточная связь ненасыщаема и ненаправлена.

Для кристаллов с Ван-дер-Ваальсовыми связями характерны летучесть, легкоплавкость, отсутствие тепло- и электропроводности.

В теории реальных газов Ван-дер-Ваальса выражение для энергии взаимодействия включает два члена: один соответствует притяжению между молекулами, а второй – отталкиванию.

Для кристаллов с остаточной связью вклад от энергии отталкивания в энергию решетки можно представить также как для ионных кристаллов: , где R – расстояние между центрами молекул.

Выражение для энергии притяжения складывается из трех слагаемых:

Все три слагаемых связаны с дипольными взаимодействиями, но происхождение диполей различно.

U₁ – энергия ориентационных взаимодействий (обе молекулы полярны) — 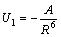. Величина А положительна и зависит от величины дипольного момента молекул и температуры, она тем больше, чем больше дипольный момент и чем меньше температура.

U₂ – энергия индукционных взаимодействий (одна молекула полярна) — . Величина В зависит от дипольного момента молекул и их поляризуемости. Очевидно, что В меньше, чем А.

U₃ – энергия дисперсионных взаимодействий (две молекулы неполярны) — . Величина С зависит от поляризуемости молекул и от собственной частоты колебаний молекул.

В полярных молекулах наиболее сильна ориентационная составляющая, в неполярных – дисперсионная. При подсчете энергии решетки молекулярных кристаллов по формуле:

выяснилось, что U₂ — U_отт, поэтому выражение приобретает вид:

Рассчитанные значения энергии очень малы и лежат в пределах нескольких килокалорий на моль, например для кристалла кислорода она равна 1,46 ккал/моль.

Металлические кристаллы

Металлическая химическая связь образуется между атомами металлов. При образовании кристаллической решетки атомы сближаются до касания, валентные орбитали соседних атомов перекрываются, в силу чего электроны свободно перемещаются с орбитали одного атома на свободную и близкую по энергии соседних атомов. В результате этого в кристаллической решетке металла возникают обобществленные свободные электроны, которые непрерывно перемещаются между положительно заряженными ионами узлов решетки, электростатически связывая их в единое целое.

Металлическая связь – нелокализованная химическая связь. Металл – плотноупакованная структура из катионов, погруженных в «электронный газ».

Металлическая связь характеризуется: ненаправленностью, ненасыщаемостью, небольшим числом валентных электронов и большим числом свободных орбиталей

Для металлических кристаллов характерны высокие координационные числа, плотные и плотнейшие упаковки частиц, высокие тепло- и электропроводность, ковкость, невысокие температуры плавления и кипения.

Теория химической связи в кристаллах металлов – зонная теория. Согласно зонной теории энергетические уровни, на которых находятся валентныеэлектроны, образуют валентную зону, над ней находится зона проводимости, которая образуется из совокупности несвязывающих орбиталей и может быть потенциально занята электронами. Если между ними существует энергетическая щель, не занятая электронами, то она называется запрещенной зоной.

Энергию взаимодействия атомов в типичном металле можно рассмотреть условно с позиций ионной модели, если считать, что электростатическое притяжение остовов и электронов приводит к возникновению сил притяжения. В рассматриваемой «ионной» модели металла притяжение можно оценить по уравнению:

,

где z – заряд остова, R – межъядерное расстояние, R/2 (радиус атома) — наиболее «вероятное» расстояние остов – электрон. Силы притяжения должны при некотором R = R₀ уравновешиваться силами отталкивания иного происхождения. Отталкивание между атомами можно считать обусловленным кинетическим движение электронного газа. Тогда силы отталкивания в металле сводятся к давлению электронного газа, зависящему от его плотности, но не от температуры. При предположении о чисто кинетической природе сил отталкивания в металлах энергия решетки металла представляется в виде:

,

и поскольку в состоянии равновесия кинетическая энергия составляет половину потенциальной, то получим:

.

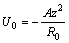
Для щелочных металлов энергия изменяется от 183 ккал/моль для лития до 105 ккал/моль для цезия.

Видео:Леменовский Д. А. - Неорганическая химия I - Кристаллические решетки и их энергииСкачать

Расчет энергетической прочности ионной решетки

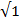
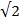
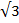
В ионном кристалле ион одного знака окружает слой противоположно заряженных ионов, затем следует слой ионов того же знака и т.д. Рассмотрим ионный кристалл типа NaCl (рис. 1.4 а), в первой координационной сфере которого находятся 6 ионов противоположного знака на расстоянии R = а/2, где R — расстояние между центрами ионов, a – период кубической решетки; во второй координационной сфере находятся 12 ионов того же знака на расстоянии R , в третьей сфере – 8 ионов противоположного типа на расстоянии R и т.д.

Энергия кулоновского взаимодействия центрального иона со всем его окружением будет выражаться суммой

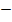
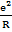
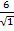
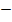
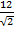
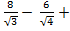
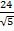
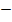
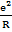
U = ( + …) = A . (1.1)

В сумме слагаемых, записанных в скобках, числителем являются координационные числа, знаменателем — относительные радиусы первой, второй и далее координационных сфер.

Величина А, получаемая в результате суммирования бесконечного ряда, заключенного в скобки, зависит от структуры, но не зависит от периода решетки. Она называется постоянной Маделунга в честь ученого, впервые (в 1918 г.) рассчитавшего такие суммы для наиболее важных решеток.

Постоянные Маделунга для различных структур приведены в табл. 1.2.

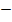
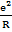
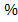
Энергия кулоновского взаимодействия ионов в изолированной молекуле равна , ( т.е. А = 1). В кристалле энергия взаимодействия возрастает примерно на 75 .

Если заряды ионов отличны от 1, например, для кристалла 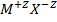, энергия кулоновского взаимодействия равна

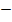
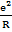
U = A Z 2 (1.2)

При сближении ионов помимо энергии притяжения следует учитывать энергию сил отталкивания.

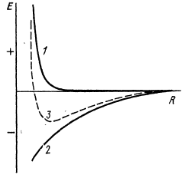
Для любого типа взаимодействия атомов потенциальная энергия складывается из энергий притяжения и отталкивания – рис.1.10.

Константы Маделунга для различных структур

U = + (p , (1.3)

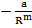
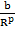
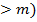
где первое слагаемое соответствует энергии притяжения, второе – отталкивания.

При m = 1 и р = 5 – 12 формула (1.3) соответствует сильному взаимодействию и выражает энергию в ионном кристалле; при m = 6 и р = 12 соответствует наиболее слабому взаимодействию и выражает энергию молекулярных кристаллов, в которых силами взаимодействия являются дисперсионные силы (силы Ван-дер-Ваальса).

Рис.1.10. Потенциальная энергия взаимодействия для любого типа химической связи в зависимости от межатомного расстояния: 1 – отталкивания, 2 – притяжения, 3 — суммарная энергия

Энергия отталкивания может быть выражена и через экспоненциальную функцию, тогда

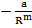
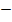
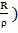
U = + В exp ( , (1.4)

где 𝜌 является некоторой константой.

Для ионного кристалла с учетом формулы (1.1) выражения для энергии (1.3) и (1.4) имеют вид

U = 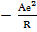+ b/R n , (1.5)

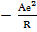
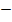
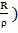
U = + В exp ( . (1.6)

В состоянии равновесия энергия решетки минимальна, для равновесного межатомного расстояния R₀ выполняется условие экстремума

( )_{R = Ro} = , (1.7)

( )_{R = Ro} = . (1.8)

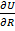
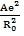
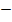
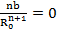
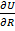
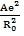
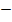
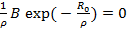
Это позволяет исключить константы b и В и перейти к уравнениям

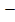
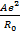
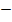
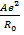
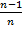
U= (1 — ) = , (1.9)

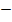
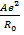
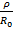
U = (1 — ). (1.10)

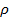
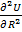
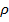
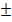
Уравнение (1.9) называется уравнением Борна-Ланде, а (1.10) – Борна-Майера. Неизвестные параметры отталкивания n и могут быть определены из данных по сжимаемости кристаллов, которая связана со второй производной . Величина n изменяется от 6 для галогенидов Li до 13 для галогенидов Ag. Для не очень малых ионов щелочных металлов (NaCl, KCl) n = 9. Среднее значение оказалось более постоянным и равным (0, 035 0,005) нм, при средних значениях межатомных расстояний R₀ = 0,3 нм, энергия отталкивания составляет около 1/10 энергии решетки.

Энергетическая прочность решетки рассчитывается для 1моля и берется с обратным знаком:

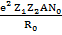
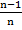
U = , (1.11)

где Z₁, Z₂ – заряды ионов, N₀ – число Авогадро. Формула (1.11) называется уравнением Борна.

Энергетическая прочность решетки – это та энергия, которая выделяется при образовании ионного кристалла из бесконечно удаленных ионов. Еще один способ определения энергетической прочности ионного кристалла – использование для расчета кругового процесса Борна – Габера.

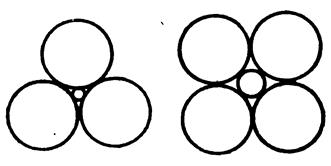
Запишем цикл Борна – Габера для ионного кристалла МХ, где М – атом металла, Х – атом галогена. В квадратных скобках обозначены вещества в кристаллическом состоянии, в круглых скобках – вещества в газообразном состоянии. Рядом со стрелками, показывающими переход из одного состояния в другое, записаны энергетические изменения: энергия, выделяемая системой, считается со знаком (+), а затрачиваемая – со знаком ( — ):

.

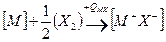
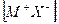
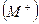
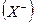
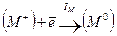
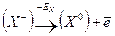
Для того, чтобы кристалл разложить на ионы и , требуется затратить энергию решетки U_MX ; при превращении ионов в нейтральные атомы выделяется энергия ионизации катиона I_M, а энергия E_X, равная сродству галогена к электрону, затрачивается:

,

;

при конденсации атомов металла освобождается энергия сублимации S_M, а при образовании молекулы (Х₂) из двух атомов галогена – выделяется энергия диссоциации молекулы на атомы D_X. (Круговой процесс записывается для одного атома галогена в соответствии с химической формулой кристалла). Наконец, из кристалла металла [M] и газообразного галогена (Х₂) снова возникает исходный кристалл 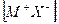с освобождением теплоты образования кристалла из простых веществ Q_MX.

Так как в круговом процессе нет потерь энергии, составим баланс энергии:

,

. (1.12)

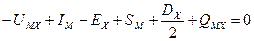
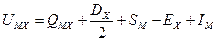
Все величины, стоящие в правой части равенства, могут быть определены экспериментально (из таблиц физико-хими- ческих величин). Поэтому такой метод определения энергии решетки называется «экспериментальным».

Энергия образования кристалла из простых веществ Q_MX с точностью до знака совпадает с энтальпией их образования из простых веществ .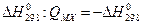

Для всех энергетических величин расчет ведется на 1 моль вещества, поэтому энергию сродства к электрону и энергию ионизации из электроновольт переводят в джоули на моль. 1 эВ = 1,6∙10 –19 Дж. Умножив на число Авогадро N_A = 6,02∙10 23 моль –1 , получим 96,48 кДж/моль.

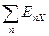
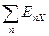
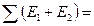
Если заряд аниона отличен от единицы, то вместо Е_Х надо записать энергию присоединения п электронов , при этом знак перед изменится на противоположный, так как энергия выделяется лишь при присоединении одного электрона к нейтральному атому, а при присоединении двух и более электронов энергия затрачивается. Например, для кислорода Е₁ = 1,46 эВ (сродство к электрону); а при присоединении двух электронов – 6,7 эВ.

Если заряд катиона отличен от единицы, то вместо I_M нужно взять сумму энергий ионизации .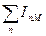

Круговой процесс записывается для всех ионов, которые входят в химическую формулу кристалла, например, для кристалла 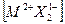в круговом процессе будут участвовать один атом металла и два атома галогена.

Если второй компонент не образует молекулы, а находится в твердом состоянии, например, сера, то вместо D_X следует брать S_X:

.

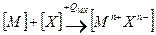
Формула для расчета прочности решетки примет вид

. (1.13)

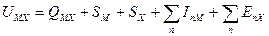
Ионные радиусы

По кратчайшему расстоянию в кристаллической решетке атомы или ионы касаются друг друга. Межионное (кратчайшее) расстояние R₀ в ионном кристалле представляют как сумму радиусов катиона r_k и аниона r_a : R₀ = r_k + r_a .

Существуют различные таблицы ионных радиусов, например, Гольдшмидта (эмпирические), Полинга (теоретические), Захариасена («эмпирико-теоретические») и др.

Значение ионного радиуса для одного и того же атома зависит от заряда иона: у катионов с увеличением заряда ионный радиус уменьшается, а у анионов – наоборот, возрастает.

Для большинства ионных решеток структура зависит от соотношения ионных радиусов. Кулоновское взаимодействие между ионами является ненаправленным и ненасыщенным.

Ненасыщенность проявляется в том, что каждый ион стремится приблизить к себе как можно больше противоположно заряженных ионов, т.е. образовать структуру с возможно более высоким координационным числом, т.е. создать плотную упаковку. Поэтому координационное число растет с увеличением размера катиона – рис.1.11.

Пределы изменения отношения радиуса катиона к радиусу аниона k = r_к/r_а , рассчитанные Магнусом и Гольдшмидтом для структур с различными координационными числами, приведены в таблице 1.3.

Рис. 1.11. Связь между конфигурацией атомов в координационной сфере и отношением ионных радиусов k = r_к/r_а

Связь отношения ионных радиусов с координационными

числами ионных решеток

Ионные радиусы зависят от координационного числа.

Координационное число записывается в виде нижнего индекса у ионного радиуса, например, r₄, r₆, r₈, r₁₂.

Обычно в таблицах указываются радиусы для к.ч. = 6, что соответствует решетке типа NaCl.

Уменьшение к.ч. приводит к уменьшению ионных радиусов: при переходе от к.ч. = 12 к к.ч. = 6 – на 12 %, от к.ч. = 8 к к.ч. = 6 – на 4 %, от к.ч. = 4 к к.ч. = 6 увеличивается на 6 % .

Далеко не все структуры подчиняются правилу отношения ионных радиусов . Особенно это касается ионов с большими зарядами (Si +4 , P +5 , S +6 , I +7 ), т.к. такие большие заряды энергетически невыгодны. Факт образования одними и теми же веществами модификаций с разными к.ч. свидетельствует о том, что проблема образования структур не может быть сведена к упаковке шаров данного диаметра.

💥 Видео

Еремин Н. Н. - Кристаллохимия. Часть 1 - Лекция 6Скачать

Уравнение БернуллиСкачать

Born-Lande equationСкачать

Определение расстояния по угловой величинеСкачать

Леменовский Д. А. - Неорганическая химия I - Энергия химической связи в ионных соединенияхСкачать

Мнимые числа реальны: #13 Поверхности Римана [Welch Labs]Скачать

Коробов М. В. - Физическая химия. Часть 1 - Основные понятия, свойства системыСкачать

Born Lande Equation : Lattice Energy Of Ionic Crystal- Very Important Derivation.Скачать

Предельные вероятности состоянийСкачать

Эффект Магнуса и уравнение БернуллиСкачать

4.1 Однородные волновые уравнения ГельмгольцаСкачать

✓ Теорема Больцано — Вейерштрасса. Подпоследовательности | матан #012 | Борис Трушин |Скачать

Консультация по курсу "Основы современной физики". Билет №3Скачать

Электронные формулы d-элементов. Явление проскока электрона.Скачать

Сопротивление материалов. Лекция: потеницальная энергия и теорема КастеллианоСкачать

Про константу Ридберга и про ридберговский атомСкачать

Тема 8. Колебательный контур. Свободные электромагнитные колебания в контуре. Формула ТомсонаСкачать