Уравнение больцмана постоянная больцмана если бы

Постоянная Больцмана, представляющая собой коэффициент, равный k = 1 , 38 · 10 — 23 Д ж К , является частью значительного числа формул в физике. Она получила свое название по имени австрийского физика – одного из основоположников молекулярно-кинетической теории. Сформулируем определение постоянной Больцмана:

Постоянной Больцмана называется физическая постоянная, с помощью которой определяется связь между энергией и температурой.

Не следует путать ее с постоянной Стефана-Больцмана, связанной с излучением энергии абсолютно твердого тела.

Существуют различные методы вычисления данного коэффициента. В рамках этой статьи мы рассмотрим два их них.

Видео:Распределение Максвелла — Больцмана (часть 6) | Термодинамика | ФизикаСкачать

Нахождение постоянной Больцмана через уравнение идеального газа

Данная постоянная может быть найдена с помощью уравнения, описывающего состояние идеального газа. Опытным путем можно определить, что нагревание любого газа от T 0 = 273 К до T 1 = 373 К приводит к изменению его давления от p 0 = 1 , 013 · 10 5 П а до p 0 = 1 , 38 · 10 5 П а . Это достаточно простой эксперимент, который может быть проведен даже просто с воздухом. Для измерения температуры при этом нужно использовать термометр, а давления – манометр. При этом важно помнить, что количество молекул в моле любого газа примерно равно 6 · 10 23 , а объем при давлении в 1 а т м равен V = 22 , 4 л . С учетом всех названных параметров можно перейти к вычислению постоянной Больцмана k :

Для этого запишем уравнение дважды, подставив в него параметры состояний.

Зная результат, можем найти значение параметра k :

Видео:Модель распределения Больцмана.Скачать

Нахождение постоянной Больцмана через формулу броуновского движения

Для второго способа вычисления нам также потребуется провести эксперимент. Для него нужно взять небольшое зеркало и подвесить в воздухе с помощью упругой нитки. Допустим, что система зеркало-воздух находится в стабильном состоянии (статическом равновесии). Молекулы воздуха ударяют в зеркало, которое, по сути, ведет себя как броуновская частица. Однако с учетом его подвешенного состояния мы можем наблюдать вращательные колебания вокруг определенной оси, совпадающей с подвесом (вертикально направленной нитью). Теперь направим на поверхность зеркала луч света. Даже при незначительных движениях и поворотах зеркала отражающийся в нем луч будет заметно смещаться. Это дает нам возможность измерить вращательные колебания объекта.

Обозначив модуль кручения как L , момент инерции зеркала по отношению к оси вращения как J , а угол поворота зеркала как φ , можем записать уравнение колебаний следующего вида:

Минус в уравнении связан с направлением момента сил упругости, который стремится вернуть зеркало в равновесное положение. Теперь произведем умножение обеих частей на φ , проинтегрируем результат и получим:

Следующее уравнение является законом сохранения энергии, который будет выполняться для данных колебаний (то есть потенциальная энергия будет переходить в кинетическую и обратно). Мы можем считать эти колебания гармоническими, следовательно:

При выведении одной из формул ранее мы использовали закон равномерного распределения энергии по степеням свободы. Значит, можем записать так:

Как мы уже говорили, угол поворота можно измерить. Так, если температура будет равна приблизительно 290 К , а модуль кручения L ≈ 10 — 15 Н · м ; » open=» φ ≈ 4 · 10 — 6 , то рассчитать значение нужного нам коэффициента можно так:

Следовательно, зная основы броуновского движения, мы можем найти постоянную Больцмана с помощью измерения макропараметров.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Значение постоянной Больцмана

Значение изучаемого коэффициента состоит в том, что с его помощью можно связать параметры микромира с теми параметрами, что описывают макромир, например, термодинамическую температуру с энергией поступательного движения молекул:

» open=» E = 3 2 k T .

Этот коэффициент входит в уравнения средней энергии молекулы, состояния идеального газа, кинетической теории газа, распределение Больцмана-Максвелла и многие другие. Также постоянная Больцмана необходима для того, чтобы определить энтропию. Она играет важную роль при изучении полупроводников, например, в уравнении, описывающем зависимость электропроводности от температуры.

Условие: вычислите среднюю энергию молекулы газа, состоящего из N -атомных молекул при температуре T , зная, что у молекул возбуждены все степени свободы – вращательные, поступательные, колебательные. Все молекулы считать объемными.

Энергия равномерно распределяется по степеням свободы на каждую ее степень, значит, на эти степени будет приходиться одинаковая кинетическая энергия. Она будет равна » open=» ε i = 1 2 k T . Тогда для вычисления средней энергии мы можем использовать формулу:

» open=» ε = i 2 k T , где i = m p o s t + m υ r + 2 m k o l представляет собой сумму поступательных вращательных степеней свободы. Буквой k обозначена постоянная Больцмана.

Переходим к определению количества степеней свободы молекулы:

m p o s t = 3 , m υ r = 3 , значит, m k o l = 3 N — 6 .

i = 6 + 6 N — 12 = 6 N — 6 ; » open=» ε = 6 N — 6 2 k T = 3 N — 3 k T .

Ответ: при данных условиях средняя энергия молекулы будет равна » open=» ε = 3 N — 3 k T .

Условие: есть смесь двух идеальных газов, плотность которых в нормальных условиях равна p. Определите, какова будет концентрация одного газа в смеси при условии, что мы знаем молярные массы обоих газов μ 1 , μ 2 .

Сначала вычислим общую массу смеси.

m = ρ V = N 1 m 01 + N 2 m 02 = n 1 V m 01 + n 2 V m 02 → ρ = n 1 m 01 + n 2 m 02 .

Параметр m 01 обозначает массу молекулы одного газа, m 02 – массу молекулы другого, n 2 – концентрацию молекул одного газа, n 2 – концентрацию второго. Плотность смеси равна ρ .

Теперь из данного уравнения выразим концентрацию первого газа:

n 1 = ρ — n 2 m 02 m 01 ; n 2 = n — n 1 → n 1 = ρ — ( n — n 1 ) m 02 m 01 → n 1 = ρ — n m 02 + n 1 m 02 m 01 → n 1 m 01 — n 1 m 02 = ρ — n m 02 → n 1 ( m 01 — m 02 ) = ρ — n m 02 .

Далее нам потребуется уравнение, описывающее состояние идеального газа:

p = n k T → n = p k T .

Подставим полученное равнее значение:

n 1 ( m 01 — m 02 ) = ρ — p k T m 02 → n 1 = ρ — p k T m 02 ( m 01 — m 02 ) .

Поскольку молярные массы газов нам известны, мы можем найти массы молекул первого и второго газа:

m 01 = μ 1 N A , m 02 = μ 2 N A .

Также мы знаем, что смесь газов находится в нормальных условиях, т.е. давление равно 1 а т м , а температура 290 К . Значит, мы можем считать задачу решенной.

Ответ: в данных условиях рассчитать концентрацию одного из газов можно как n 1 = ρ — p k T m 02 ( m 01 — m 02 ) , где m 01 = μ 1 N A , m 02 = μ 2 N A .

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Постоянная Больцмана: значение и физический смысл

Как точная количественная наука, физика не обходится без набора очень важных постоянных, входящих в качестве универсальных коэффициентов в уравнения, устанавливающие связь между теми или иными величинами. Это фундаментальные константы, благодаря которым подобные соотношения приобретают инвариантность и способны объяснять поведение физических систем на различном масштабе.

К числу таких параметров, характеризующих присущие материи нашей Вселенной свойства, относится и постоянная Больцмана – величина, входящая в ряд важнейших уравнений. Однако прежде чем обращаться к рассмотрению ее особенностей и значения, нельзя не сказать нескольких слов об ученом, чье имя она носит.

Видео:Тепловое излучение и закон смещения ВинаСкачать

Людвиг Больцман: научные заслуги

Один из крупнейших ученых XIX столетия, австриец Людвиг Больцман (1844–1906) внес существенный вклад в развитие молекулярно-кинетической теории, став одним из создателей статистической механики. Был автором эргодической гипотезы, статистического метода в описании идеального газа, основного уравнения физической кинетики. Много работал над вопросами термодинамики (H-теорема Больцмана, статистический принцип для второго начала термодинамики), теории излучения (закон Стефана – Больцмана). Также затрагивал в своих работах некоторые вопросы электродинамики, оптики и других разделов физики. Имя его увековечено в двух физических константах, речь о которых пойдет ниже.

Людвиг Больцман был убежденным и последовательным сторонником теории атомно-молекулярного строения вещества. На протяжении многих лет он вынужден был бороться с непониманием и неприятием этих идей в научном сообществе того времени, когда многие физики полагали атомы и молекулы излишней абстракцией, в лучшем случае условным приемом, служащим для удобства расчетов. Мучительное заболевание и нападки консервативно настроенных коллег спровоцировали у Больцмана тяжелую депрессию, не вынеся которой, выдающийся ученый покончил с собой. На могильном памятнике, над бюстом Больцмана, как знак признания его заслуг, выбито уравнение S = k∙logW – один из результатов его плодотворной научной деятельности. Константа k в этом уравнении – постоянная Больцмана.

Видео:Атмосфера #4 | Кинетическое уравнение БольцманаСкачать

Энергия молекул и температура вещества

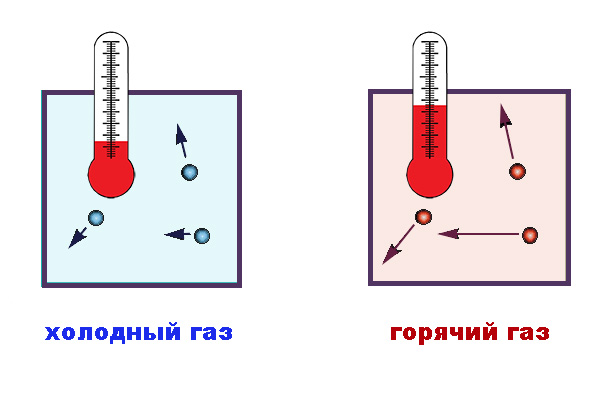
Понятие температуры служит для характеристики степени нагретости того или иного тела. В физике применяется абсолютная шкала температур, в основу которой положен вывод молекулярно-кинетической теории о температуре как о мере, отражающей величину энергии теплового движения частиц вещества (имеется в виду, конечно, средняя кинетическая энергия множества частиц).

Как принятый в системе СИ джоуль, так и эрг, используемый в системе СГС, – слишком большие единицы для выражения энергии молекул, да и практически было весьма затруднительно измерять температуру подобным образом. Удобной единицей температуры является градус, а измерение проводится опосредованно, через регистрацию изменяющихся макроскопических характеристик вещества – например, объема.

Видео:Урок 148. Тепловое равновесие. Температура.Скачать

Как соотносятся энергия и температура

Для расчета состояний реального вещества при температурах и давлениях, близких к нормальным, с успехом используется модель идеального газа, то есть такого, размер молекулы которого много меньше объема, занимаемого некоторым количеством газа, а расстояние между частицами значительно превышает радиус их взаимодействия. Исходя из уравнений кинетической теории, средняя энергия таких частиц определяется как E_ср = 3/2∙kT, где E – кинетическая энергия, T – температура, а 3/2∙k – коэффициент пропорциональности, введенный Больцманом. Число 3 здесь характеризует количество степеней свободы поступательного движения молекул в трех пространственных измерениях.

Величина k, которую впоследствии в честь австрийского физика назвали константой Больцмана, показывает, какую часть джоуля или эрга содержит в себе один градус. Иными словами, ее значение определяет, насколько увеличивается статистически, в среднем, энергия теплового хаотического движения одной частицы одноатомного идеального газа при повышении температуры на 1 градус.

Видео:Связь между температурой и кинетической энергией молекул газа Постоянная БольцманаСкачать

Во сколько раз градус меньше джоуля

Численное значение этой константы можно получить различными способами, например, через измерение абсолютной температуры и давления, используя уравнение идеального газа, или с применением модели броуновского движения. Теоретическое выведение данной величины на современном уровне знаний не представляется возможным.

Постоянная Больцмана равна 1,38 × 10 -23 Дж/К (здесь К – кельвин, градус абсолютной температурной шкалы). Для коллектива частиц в 1 моле идеального газа (22,4 литра) коэффициент, связывающий энергию с температурой (универсальная газовая постоянная), получается умножением константы Больцмана на число Авогадро (количество молекул в моле): R = kN_A, и составляет 8,31 Дж/(моль∙кельвин). Однако, в отличие от последней, константа Больцмана носит более универсальный характер, поскольку входит и в другие важные соотношения, а также сама служит для определения еще одной физической постоянной.

Видео:Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Статистическое распределение энергий молекул

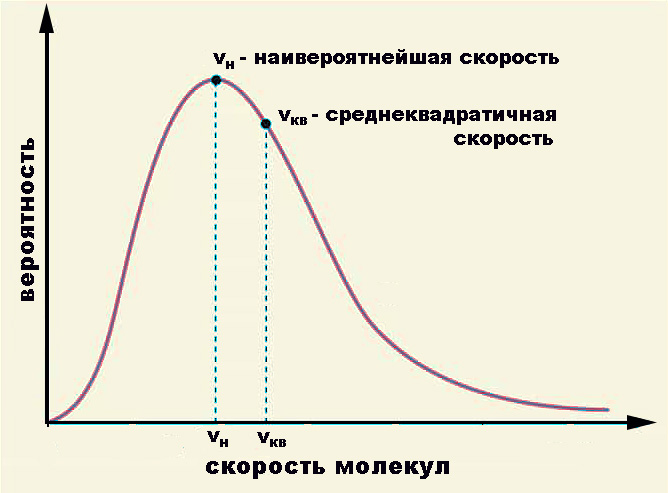
Поскольку состояния вещества макроскопического порядка представляют собой результат поведения большой совокупности частиц, они описываются с помощью статистических методов. К последним относится и выяснение того, как распределяются энергетические параметры молекул газа:

• Максвелловское распределение кинетических энергий (и скоростей). Оно показывает, что в газе, пребывающем в состоянии равновесия, большинство молекул обладает скоростями, близкими к некоторой наиболее вероятной скорости v = √(2kT/m₀), где m₀ – масса молекулы.
• Больцмановское распределение потенциальных энергий для газов, находящихся в поле каких-либо сил, например гравитации Земли. Оно зависит от соотношения двух факторов: притяжения к Земле и хаотического теплового движения частиц газа. В итоге чем ниже потенциальная энергия молекул (ближе к поверхности планеты), тем выше их концентрация.

Оба статистических метода объединяются в распределение Максвелла – Больцмана, содержащее экспоненциальный множитель e – E/ kT , где E – сумма кинетической и потенциальной энергий, а kT – уже известная нам средняя энергия теплового движения, управляемая постоянной Больцмана.

Видео:Физика 10 класс (Урок№19 - Температура. Энергия теплового движения молекул.)Скачать

Константа k и энтропия

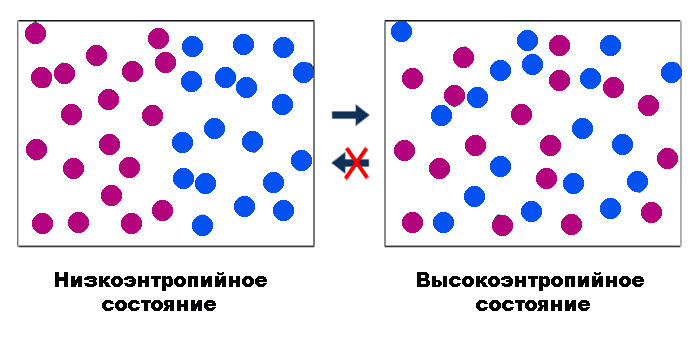
В общем смысле энтропию можно охарактеризовать как меру необратимости термодинамического процесса. Эта необратимость связана с рассеянием – диссипацией – энергии. При статистическом подходе, предложенном Больцманом, энтропия является функцией количества способов, которыми может быть реализована физическая система без изменения ее состояния: S = k∙lnW.

Здесь постоянная k задает масштаб роста энтропии с увеличением этого количества (W) вариантов реализации системы, или микросостояний. Макс Планк, который привел данную формулу к современному виду, и предложил дать константе k имя Больцмана.

Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Закон излучения Стефана – Больцмана

Физический закон, устанавливающий, как энергетическая светимость (мощность излучения на единицу поверхности) абсолютно черного тела зависит от его температуры, имеет вид j = σT 4 , то есть тело излучает пропорционально четвертой степени своей температуры. Этот закон используется, например, в астрофизике, так как излучение звезд близко по характеристикам к чернотельному.

В указанном соотношении присутствует еще одна константа, также управляющая масштабом явления. Это постоянная Стефана – Больцмана σ, которая равна приблизительно 5,67 × 10 -8 Вт/(м 2 ∙К 4 ). Размерность ее включает кельвины – значит, ясно, что и здесь участвует константа Больцмана k. Действительно, величина σ определяется как (2π 2 ∙k 4 )/(15c 2 h 3 ), где c – скорость света и h – постоянная Планка. Так что больцмановская константа, сочетаясь с другими мировыми постоянными, образует величину, опять-таки связывающую между собой энергию (мощность) и температуру – в данном случае применительно к излучению.

Видео:25. Распределение БольцманаСкачать

Физическая сущность константы Больцмана

Выше уже отмечалось, что постоянная Больцмана относится к числу так называемых фундаментальных констант. Дело не только в том, что она позволяет установить связь характеристик микроскопических явлений молекулярного уровня с параметрами процессов, наблюдаемых в макромире. И не только в том, что эта константа входит в ряд важных уравнений.

В настоящее время неизвестно, существует ли какой-либо физический принцип, на основе которого она могла бы быть выведена теоретически. Иными словами, ни из чего не следует, что значение данной константы должно быть именно таким. Мы могли бы в качестве меры соответствия кинетической энергии частиц использовать иные величины и иные единицы вместо градусов, тогда численное значение константы было бы другим, но она осталась бы постоянной величиной. Наряду с прочими фундаментальными величинами такого рода – предельной скоростью c, постоянной Планка h, элементарным зарядом e, гравитационной постоянной G, – наука принимает константу Больцмана как данность нашего мира и использует для теоретического описания протекающих в нем физических процессов.

Видео:Урок 153. Распределение молекул по скоростямСкачать

Постоянная Больцмана

Людвиг Больцман — один из создателей молекулярно-кинетической теории газов, на которой зиждется современная картина взаимосвязи между движением атомов и молекул с одной стороны и макроскопическими свойствами материи, такими как температура и давление, с другой. В рамках такой картины давление газа обусловлено упругими ударами молекул газа о стенки сосуда, а температура — скоростью движения молекул (а точнее, их кинетической энергией).Чем быстрее движутся молекулы, тем выше температура.

Постоянная Больцмана дает возможность напрямую связать характеристики микромира с характеристиками макромира — в частности, с показаниями термометра. Вот ключевая формула, устанавливающая это соотношение:

где m и v — соответственно масса и средняя скорость движения молекул газа, Т — температура газа (по абсолютной шкале Кельвина), а k — постоянная Больцмана. Это уравнение прокладывает мостик между двумя мирами, связывая характеристики атомного уровня (в левой части) с объемными свойствами (в правой части), которые можно измерить при помощи человеческих приборов, в данном случае термометров. Эту связь обеспечивает постоянная Больцмана k, равная .

Раздел физики, изучающий связи между явлениями микромира и макромира, называется статистическая механика. В этом разделе едва ли найдется уравнение или формула, в которых не фигурировала бы постоянная Больцмана. Одно из таких соотношений было выведено самим австрийцем, и называется оно просто уравнение Больцмана:

где S — энтропия системы (см. Второе начало термодинамики), p — так называемый статистический вес (очень важный элемент статистического подхода), а b — еще одна константа.

Всю жизнь Людвиг Больцман в буквальном смысле опережал свое время, разрабатывая основы современной атомной теории строения материи, вступая в яростные споры с подавляющим консервативным большинством современного ему научного сообщества, считавшего атомы лишь условностью, удобной для расчетов, но не объектами реального мира. Когда его статистический подход не встретил ни малейшего понимания даже после появления специальной теории относительности, Больцман в минуту глубокой депрессии покончил с собой. Уравнение Больцмана высечено на его надгробном памятнике.

Австрийский физик. Родился в Вене в семье госслужащего. Учился в Венском университете на одном курсе с Йозефом Стефаном (см. Закон Стефана—Больцмана). Защитившись в 1866 году, продолжил научную карьеру, занимая в разное время профессорские должности на кафедрах физики и математики университетов Граца, Вены, Мюнхена и Лейпцига. Будучи одним из главных сторонников реальности существования атомов, сделал ряд выдающихся теоретических открытий, проливающих свет на то, каким образом явления на атомном уровне сказываются на физических свойствах и поведении материи.

🎥 Видео

2 Лекция 16 Формула БольцманаСкачать

Урок 149. Абсолютная температурная шкалаСкачать

Грибов В. А. - Термодинамика и статистическая физика - Н-теорема БольцманаСкачать

Термодинамика Л8.4. Распределение БольцманаСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Распределение БольцманаСкачать

Савченко А. М. - Термодинамика и статистическая физика II - Уравнение Власова. Уравнение БольцманаСкачать