Уравнение больцмана его физический смысл

Видео:Распределение Максвелла — Больцмана (часть 6) | Термодинамика | ФизикаСкачать

Постоянная Больцмана: значение и физический смысл

Как точная количественная наука, физика не обходится без набора очень важных постоянных, входящих в качестве универсальных коэффициентов в уравнения, устанавливающие связь между теми или иными величинами. Это фундаментальные константы, благодаря которым подобные соотношения приобретают инвариантность и способны объяснять поведение физических систем на различном масштабе.

К числу таких параметров, характеризующих присущие материи нашей Вселенной свойства, относится и постоянная Больцмана – величина, входящая в ряд важнейших уравнений. Однако прежде чем обращаться к рассмотрению ее особенностей и значения, нельзя не сказать нескольких слов об ученом, чье имя она носит.

Видео:Атмосфера #4 | Кинетическое уравнение БольцманаСкачать

Людвиг Больцман: научные заслуги

Один из крупнейших ученых XIX столетия, австриец Людвиг Больцман (1844–1906) внес существенный вклад в развитие молекулярно-кинетической теории, став одним из создателей статистической механики. Был автором эргодической гипотезы, статистического метода в описании идеального газа, основного уравнения физической кинетики. Много работал над вопросами термодинамики (H-теорема Больцмана, статистический принцип для второго начала термодинамики), теории излучения (закон Стефана – Больцмана). Также затрагивал в своих работах некоторые вопросы электродинамики, оптики и других разделов физики. Имя его увековечено в двух физических константах, речь о которых пойдет ниже.

Людвиг Больцман был убежденным и последовательным сторонником теории атомно-молекулярного строения вещества. На протяжении многих лет он вынужден был бороться с непониманием и неприятием этих идей в научном сообществе того времени, когда многие физики полагали атомы и молекулы излишней абстракцией, в лучшем случае условным приемом, служащим для удобства расчетов. Мучительное заболевание и нападки консервативно настроенных коллег спровоцировали у Больцмана тяжелую депрессию, не вынеся которой, выдающийся ученый покончил с собой. На могильном памятнике, над бюстом Больцмана, как знак признания его заслуг, выбито уравнение S = k∙logW – один из результатов его плодотворной научной деятельности. Константа k в этом уравнении – постоянная Больцмана.

Видео:Рассмотрение темы: "Распределение Максвелла"Скачать

Энергия молекул и температура вещества

Понятие температуры служит для характеристики степени нагретости того или иного тела. В физике применяется абсолютная шкала температур, в основу которой положен вывод молекулярно-кинетической теории о температуре как о мере, отражающей величину энергии теплового движения частиц вещества (имеется в виду, конечно, средняя кинетическая энергия множества частиц).

Как принятый в системе СИ джоуль, так и эрг, используемый в системе СГС, – слишком большие единицы для выражения энергии молекул, да и практически было весьма затруднительно измерять температуру подобным образом. Удобной единицей температуры является градус, а измерение проводится опосредованно, через регистрацию изменяющихся макроскопических характеристик вещества – например, объема.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Как соотносятся энергия и температура

Для расчета состояний реального вещества при температурах и давлениях, близких к нормальным, с успехом используется модель идеального газа, то есть такого, размер молекулы которого много меньше объема, занимаемого некоторым количеством газа, а расстояние между частицами значительно превышает радиус их взаимодействия. Исходя из уравнений кинетической теории, средняя энергия таких частиц определяется как E_ср = 3/2∙kT, где E – кинетическая энергия, T – температура, а 3/2∙k – коэффициент пропорциональности, введенный Больцманом. Число 3 здесь характеризует количество степеней свободы поступательного движения молекул в трех пространственных измерениях.

Величина k, которую впоследствии в честь австрийского физика назвали константой Больцмана, показывает, какую часть джоуля или эрга содержит в себе один градус. Иными словами, ее значение определяет, насколько увеличивается статистически, в среднем, энергия теплового хаотического движения одной частицы одноатомного идеального газа при повышении температуры на 1 градус.

Видео:Модель распределения Больцмана.Скачать

Во сколько раз градус меньше джоуля

Численное значение этой константы можно получить различными способами, например, через измерение абсолютной температуры и давления, используя уравнение идеального газа, или с применением модели броуновского движения. Теоретическое выведение данной величины на современном уровне знаний не представляется возможным.

Постоянная Больцмана равна 1,38 × 10 -23 Дж/К (здесь К – кельвин, градус абсолютной температурной шкалы). Для коллектива частиц в 1 моле идеального газа (22,4 литра) коэффициент, связывающий энергию с температурой (универсальная газовая постоянная), получается умножением константы Больцмана на число Авогадро (количество молекул в моле): R = kN_A, и составляет 8,31 Дж/(моль∙кельвин). Однако, в отличие от последней, константа Больцмана носит более универсальный характер, поскольку входит и в другие важные соотношения, а также сама служит для определения еще одной физической постоянной.

Видео:ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Статистическое распределение энергий молекул

Поскольку состояния вещества макроскопического порядка представляют собой результат поведения большой совокупности частиц, они описываются с помощью статистических методов. К последним относится и выяснение того, как распределяются энергетические параметры молекул газа:

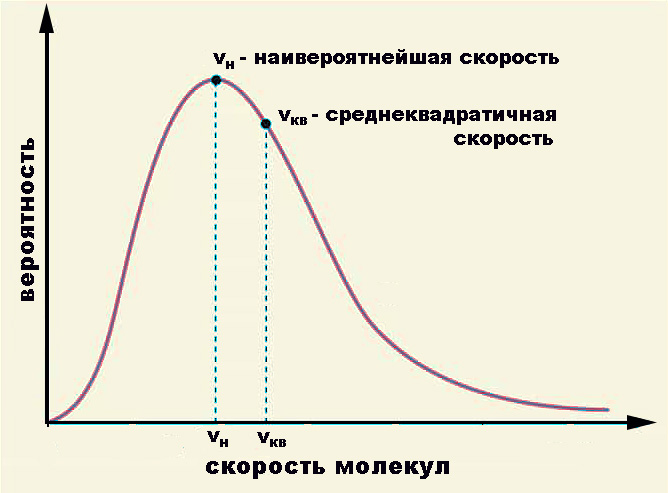
• Максвелловское распределение кинетических энергий (и скоростей). Оно показывает, что в газе, пребывающем в состоянии равновесия, большинство молекул обладает скоростями, близкими к некоторой наиболее вероятной скорости v = √(2kT/m₀), где m₀ – масса молекулы.
• Больцмановское распределение потенциальных энергий для газов, находящихся в поле каких-либо сил, например гравитации Земли. Оно зависит от соотношения двух факторов: притяжения к Земле и хаотического теплового движения частиц газа. В итоге чем ниже потенциальная энергия молекул (ближе к поверхности планеты), тем выше их концентрация.

Оба статистических метода объединяются в распределение Максвелла – Больцмана, содержащее экспоненциальный множитель e – E/ kT , где E – сумма кинетической и потенциальной энергий, а kT – уже известная нам средняя энергия теплового движения, управляемая постоянной Больцмана.

Видео:Кинетическое уравнение Больцмана: функциональный, асимптотический и численный анализСкачать

Константа k и энтропия

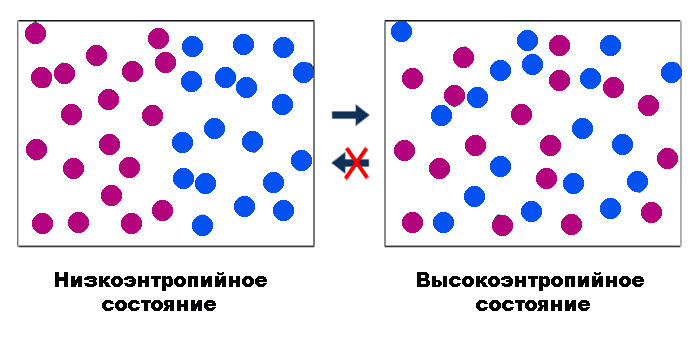
В общем смысле энтропию можно охарактеризовать как меру необратимости термодинамического процесса. Эта необратимость связана с рассеянием – диссипацией – энергии. При статистическом подходе, предложенном Больцманом, энтропия является функцией количества способов, которыми может быть реализована физическая система без изменения ее состояния: S = k∙lnW.

Здесь постоянная k задает масштаб роста энтропии с увеличением этого количества (W) вариантов реализации системы, или микросостояний. Макс Планк, который привел данную формулу к современному виду, и предложил дать константе k имя Больцмана.

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Закон излучения Стефана – Больцмана

Физический закон, устанавливающий, как энергетическая светимость (мощность излучения на единицу поверхности) абсолютно черного тела зависит от его температуры, имеет вид j = σT 4 , то есть тело излучает пропорционально четвертой степени своей температуры. Этот закон используется, например, в астрофизике, так как излучение звезд близко по характеристикам к чернотельному.

В указанном соотношении присутствует еще одна константа, также управляющая масштабом явления. Это постоянная Стефана – Больцмана σ, которая равна приблизительно 5,67 × 10 -8 Вт/(м 2 ∙К 4 ). Размерность ее включает кельвины – значит, ясно, что и здесь участвует константа Больцмана k. Действительно, величина σ определяется как (2π 2 ∙k 4 )/(15c 2 h 3 ), где c – скорость света и h – постоянная Планка. Так что больцмановская константа, сочетаясь с другими мировыми постоянными, образует величину, опять-таки связывающую между собой энергию (мощность) и температуру – в данном случае применительно к излучению.

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Физическая сущность константы Больцмана

Выше уже отмечалось, что постоянная Больцмана относится к числу так называемых фундаментальных констант. Дело не только в том, что она позволяет установить связь характеристик микроскопических явлений молекулярного уровня с параметрами процессов, наблюдаемых в макромире. И не только в том, что эта константа входит в ряд важных уравнений.

В настоящее время неизвестно, существует ли какой-либо физический принцип, на основе которого она могла бы быть выведена теоретически. Иными словами, ни из чего не следует, что значение данной константы должно быть именно таким. Мы могли бы в качестве меры соответствия кинетической энергии частиц использовать иные величины и иные единицы вместо градусов, тогда численное значение константы было бы другим, но она осталась бы постоянной величиной. Наряду с прочими фундаментальными величинами такого рода – предельной скоростью c, постоянной Планка h, элементарным зарядом e, гравитационной постоянной G, – наука принимает константу Больцмана как данность нашего мира и использует для теоретического описания протекающих в нем физических процессов.

Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Молекулярно-кинетическое толкование температуры. Постоянная Больцмана

Основное уравнение молекулярно-кинетической теории идеального газа несет в себе более глубокий смысл, чем обычная формула для определения давления иде­ального газа. Для его выяснения запишем это уравнение p = (1 / 3) • nm₀v̅ 2 в несколько другом виде:

По определению m₀v̅ 2 / 2 является средней кинетической энергией поступательного движения молекулы.

Давление газа пропорционально сред­ней кинетической энергии поступательного движения молекул.

С другой стороны, из уравнения состо­яния идеального газа

Сравнив оба этих уравнения, получим:

Из этого соотношения вытекает важный вывод:

средняя кинетическая энергия моле­кул газа прямо пропорциональна его абсо­лютной температуре.

Отношение универсальной газовой по­стоянной R к постоянной Авогадро N_A так­же есть величина постоянная, которая на­зывается постоянной Больцмана k.

R / N_A = k — постоянная Больц­мана.

Физический смысл постоянной Больцмана состоит в том, что она устанавливает соотноше­ние температуры, выраженной в энергетических (Дж) и тер­модинамических (K) единицах.

Постоянная Больцмана является фундамен­тальной константой, значение которой опре­делено довольно точно:

Если это выражение подставить в фор­мулу p = (2 / 3) • nE̅, получим зависимость давления идеального газа от температуры и концентра­ции его молекул:

Это соотношение подтверждает установ­ленный экспериментально закон Шарля, согласно которому давление данной массы газа прямо пропорционально абсо­лютной температуре: p

T. Из него следует также, что

при одинаковых давлении и тем­пературе концентрация молекул во всех газах одинакова.

Таким образом, температура как макро­параметр системы характеризует состояние ее термодинамического равновесия. Материал с сайта http://worldofschool.ru

Приближение температуры те­ла к абсолютному нулю ведет к уменьшению средней кинети­ческой энергии молекул. При абсолютном нуле их поступа­тельное движение прекращает­ся. Современная наука отри­цает возможность достижения абсолютного нуля температур.

В зависимости от избранной шкалы тем­пература измеряется в градусах Цельсия или Фаренгейта либо в кельвинах. Как микро­параметр системы температура определяет среднюю кинетическую энергию значитель­ного количества молекул; как ее мера она измеряется в джоулях. Коэффициентом свя­зи между этими ее определениями является постоянная Больцмана.

Несмотря на то, что вывод о связи температуры со средней кинетической энергией моле­кул установлен для газов, он справедлив также для жидкос­тей и твердых тел.

Видео:2 Лекция 16 Формула БольцманаСкачать

Физический смысл постоянной Больцмана

Перевод статьи на английский язык без разрешения автора запрещается!
Упоминание о статье и любое использование опубликованного в статье материала в англоязычных публикациях без разрешения автора запрещается!

Логофизика. Объём как суть постоянной Больцмана

Современная теоретическая физика не знает, что энергия есть мера способности материального объекта, а температура есть мера состояния материального объекта, потому что физики не представляют, что такое способность, и не совсем понимают, что такое состояние.
Способность и состояние – это объекты (понятия) Вселенной, выражающие связь материи и движения. Способность – это «действенность» материи (материального объекта, среды, частицы), то есть реализуемая материей возможность действия (в русском языке есть слово «дееспособность», но оно в общении между людьми означает «возможность разумного поведения» или «возможность реализации возможностей» и относится только к человеку). А состояние – это уже реализованная возможность материи (материальной среды, объекта, физического тела), «тяжесть» движения.

В рассматриваемой системе отсчёта каждое физическое тело, то есть материальный объект, имеющий форму и (или) ограниченный поверхностью, имеет в каждый момент своего бытия одно из двух состояний – либо тело находится в движении, либо тело находится в покое. Движение во Вселенной складывается из комбинаций двух действий – перемещение и поворот (изменение направления перемещения). Если тело в рассматриваемой системе отсчёта перемещается, то есть изменяет своё местоположение в определённом направлении, следовательно, оно находится в движении в данной системе отсчёта и имеет скорость движения. Если тело в рассматриваемой системе отсчёта не перемещается, то есть не изменяет своё местоположение, следовательно, оно находится в покое или вращается вокруг своей оси или своего центра тяжести, имея угловую скорость вращения.

Материя имеет возможность двигаться, если она находится в покое, и также имеет возможность покоиться, если она находится в движении, – это показано в статье «Возможность как суть постоянной Планка». Соответственно, реализуемая объектом возможность движения – это способность объекта к перемещению в рассматриваемой системе отсчёта, а реализуемая объектом возможность покоя – это способность объекта вращаться, не перемещаясь относительно центра системы или начала координат. И то, и другое – это способность к действию, поскольку способность находиться в покое также подразумевает определённое движение, выражаемое словами «находиться» или «быть», ведь они отражают принадлежность объекта к системе – то, что он движется вместе с системой отсчёта. Это наглядно показывает прямую связь между способностью и состоянием – способность к действию означает способность объекта к нахождению в каком-либо состоянии (движения или покоя), то есть способность иметь состояние или способность к сохранению состояния.

Каждая способность характеризуется собственной величиной – энергией «Е», – и от этой величины зависит, соответственно, величина состояния. Так как движение сводится лишь к двум видам – перемещению и вращению, – то способностей материи быть в состоянии движения может быть всего две – способность к перемещению и способность к вращению. В статье «Способность к вращению» было показано, что способность материального объекта к вращению в рассматриваемой системе отсчёта и способность к перемещению в ней есть одна и та же способность объекта к движению, рассматриваемая с разных точек зрения на систему отсчёта – как на инерциальную или неинерциальную. Если материальный объект способен перемещаться в инерциальной системе, то величина его способности к движению – это кинетическая энергия
Ек=(1/2)*mv^2,
где m – масса объекта, v – скорость его перемещения.
Если материальный объект способен вращаться вокруг центра неинерциальной системы, то величина его способности к вращению – энергия потенциальная
Еп=(1/2)*mw^2*R^2,
где m – масса объекта, R – расстояние от центра тяжести объекта до центра системы, в которой он движется, w – угловая скорость вращения объекта вокруг центра системы отсчёта.

Если расстояние R от центра тяжести объекта до центра системы равно нулю, то есть объект вращается вокруг собственного центра тяжести и сам представляет систему отсчёта, то величина его способности к вращению – это его внутренняя энергия, являющаяся суммарной потенциальной или кинетической энергией составляющих его частей
U= ЕN,
где
N=m/m(0) – количество самостоятельных частей (молекул, атомов и пр.) в составе объекта, m – масса объекта, m(0) – масса части объекта (атома или молекулы или др.),
Е =TV(0) – энергия одной самостоятельной части объекта (молекулы, атома или др.), равная средней кинетической или потенциальной энергии частей объекта (молекул, атомов или др.), V(0) – объём части объекта (молекулы или др.), Т – температура системы, средняя величина состояния частей объекта, который в данном случае является системой частей.

Как уже было выше сказано, способность объекта к обращению вокруг центра системы и способность к перемещению в рассматриваемой системе есть одна и та же способность объекта к движению, рассматриваемая с разных точек зрения на систему отсчёта – как на инерциальную или на неинерциальную. Поэтому величина состояния объекта в системе, в которой он передвигается относительно других объектов, – температура объекта – определяется отношением любой его энергии (кинетической или потенциальной) в данной системе к его объёму
Т=Ек/V=(1/2)*mv^2/V,
или
Т=Еп/V=(1/2)*mw^2*R^2/V.

Внутреннюю энергию объекта «U=mTV(0) / m(0)» можно также рассматривать как величину способности объекта к покою, теплоту.

Теперь вспомним термодинамику и представим себе уравнение состояния идеального газа в термодинамической системе, устанавливающее зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа
p*V(M) = R*T,
где p – давление, T – абсолютная температура, V(M) – молярный объём (объём, который занимает 1 моль газа), R – универсальная газовая постоянная, причём
R = N(A)*k,
где N(A) – число Авогадро, k – постоянная Больцмана, а
V(M) = V*M/m,
где V – объём системы, (m/M) – количество молей газа в системе, m – масса системы, M – молярная масса (масса одного моля газа).
То есть, уравнение состояния идеального газа можно записать в виде
p*V= N(A)*k*T*m/M.
С учётом того, что масса 1 моля газа равна сумме масс «m(0)» молекул газа, количество которых есть число Авогадро N(A),
M= m(0)*N(A),
уравнение состояния идеального газа записывается в виде
p*V= k*T*m/m(0),
где p – давление в системе, T – абсолютная температура системы, k – постоянная Больцмана, V – объём системы, m – масса системы, m0 – масса молекулы газа.

Отсюда выводится следующее соотношение давления и температуры в системе, заполненной идеальным газом,
p*V/k = T*m/m(0).
Это уравнение покажет физический смысл постоянной Больцмана «k», если его записать в виде
pV/V(0) = Tm/m(0), (1)
где коэффициент «k=V(0)» – это объём, который занимает в пространстве молекула газа.
Так как уравнение Клапейрона-Менделеева составлялось для идеального газа, то постоянная Больцмана «k=1,38*10^(-23)» показывает объём молекулы одноатомного газа, то есть объём одного атома.
Но вполне вероятно, что вышеприведённое равенство (1) относится не только к системе с идеальным газом, а к любой системе, заполненной реальным однородным веществом, тогда оно будет читаться следующим образом:
«Произведение давления в системе и объёма этой системы, заполненной однородной жидкостью или газом, относится к объёму молекулы этого газа или жидкости так же, как произведение температуры системы и массы системы относится к массе молекулы этого газа или жидкости».

Молекулярно-кинетическая теория построена на предположении, что молекулы газа постоянно и хаотически перемещаются. Но чтобы молекулы в системе постоянно перемещались, на них постоянно должно оказываться воздействие, ведь молекула – не вечный двигатель. Если же система открыта для тепла, то молекулы могут всего лишь колебаться около своего центра тяжести под воздействием теплового излучения. Любое колебание предполагает вращение или прямое-обратное перемещение подобно колебанию маятника, и, следовательно, каждая молекула имеет среднюю скорость перемещения и кинетическую энергию, или же потенциальную энергию вращения около центра тяжести. А значит, давление в системе может возникать не как следствие постоянных ударов молекул о стенки системы, а вследствие распределения энергии (теплоты) в системе и соответственного изменения состояния системы. Мерой состояния является температура.
Представим себе закрытый ящик с надутыми резиновыми воздушными шариками. Шарики в ящике спокойно себе висят, не двигаются и не сталкиваются, потому что никакого воздействия на них не производится. Стенки ящика прочные и несгибаемые, и объём ящика не изменяется ни при каких воздействиях. То есть ящик представляет собой ограниченную в пространстве систему – закрытую, если стенки не пропускают тепло, и также ограниченную, но открытую, если стенки пропускают внешнее тепло. В этой системе объём ящика – величина постоянная, количество шаров – величина постоянная, масса каждого шара – величина постоянная, и, следовательно, масса ящика (без массы стенок ящика и массы резиновых оболочек шаров) – величина постоянная. А объём каждого шарика – величина изменяемая, и она может изменяться от минимального значения до максимального при изменении температуры в ящике. Минимальным значением объёма шара можно считать его объём при минимально возможной температуре, а максимальным – объём, при котором между шариками в ящике исчезает свободное место, и сумма объёмов шариков становится равна объёму ящика (толщиной резиновых оболочек шариков пренебрегаем).

Если система характеризуется постоянным объёмом (V), постоянной массой составляющего её вещества (m) и постоянной массой молекулы вещества «m(0)», то для такой системы величина отношения плотности (Р – греческая буква «ро») её вещества к массе молекулы вещества является константой, а изменяемыми и друг от друга зависимыми величинами являются давление в системе (р), температура системы (Т) и объём молекулы «V(0)»
m/Vm(0) = Р/m(0) = const = p/TV(0).
Из этого предположения следует, что отношение давления в системе к её температуре равно произведению плотности вещества системы и отношения объёма молекулы вещества системы к массе молекулы
p/Т = Р*V(0)/m(0),
где Р=m/V – плотность системы, m0 – масса молекулы вещества, составляющего систему, V(0) – объём молекулы вещества. Конечно, при одноатомном веществе слово «молекула» заменяется на «атом».

Внутренняя энергия «U» системы равна сумме энергий молекул вещества системы
U= ЕN,
где N=m/m(0) – количество молекул (m(0) – масса молекулы) в системе массой «m», а энергия молекулы вычисляется как средняя кинетическая или потенциальная энергия молекул, либо как произведение объёма «V(0)» молекулы и меры её состояния «T»
Е = Ек= Еп= m(0)*v(0)^2/2= TV(0)
– кинетическая (потенциальная) энергия молекулы, v(0) – средняя скорость перемещения молекулы при её колебании в системе, V(0) – объём молекулы, Т – установившаяся температура системы, равная средней температуре молекул,
откуда с учётом равенства (1)
U= mv(0)^2/2= TV(0)*m/m(0) = TV(0)*(pV/V(0)T) = рV,
где p – давление в системе, V – объём системы, m – масса системы, v(0) – средняя скорость перемещения молекул, V(0) – объём молекулы, m(0) – масса молекулы,
то есть внутренняя энергия системы равна произведению давления в системе и объёма системы.

📹 Видео

Грибов В. А. - Термодинамика и статистическая физика - Кинетическое уравнение БольцманаСкачать

Кинетическое уравнение Больцмана (3). Макроскопические транспортные процессы. Самодиффузия (1).Скачать

Основы молекулярной физики | барометрическая формула | для взрослыхСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Урок 153. Распределение молекул по скоростямСкачать

О чем говорят уравнения Максвелла? Видео 1/2Скачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Вся суть мат. анализа за 3 мин 14 сек!Скачать

Джеймс Клерк Максвелл. Научные труды и вклад в наукуСкачать