- Закон излучения Стефана-Больцмана
- Постоянная Стефана-Больцмана
- Постоянная Больцмана
- Статистика Больцмана
- Газ Больцмана
- H-функция Больцмана
- H-теорема Больцмана
- Принцип Больцмана
- Кинетическое уравнение Больцмана
- Распределение Максвелла-Больцмана
- Формула Больцмана барометрическая
- Уравнение больцмана для идеального газа
- Постоянная Больцмана
- Нахождение постоянной Больцмана через уравнение идеального газа
- Нахождение постоянной Больцмана через формулу броуновского движения
- Значение постоянной Больцмана
- 🔍 Видео
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Закон излучения Стефана-Больцмана
Согласно закону Стефана – Больцмана плотность интегрального полусферического излучения E0 зависит только от температуры и изменяется пропорционально четвертой степени абсолютной температуры T:
Видео:Распределение Максвелла — Больцмана (часть 6) | Термодинамика | ФизикаСкачать

Постоянная Стефана-Больцмана
Стефана – Больцмана постоянная σ0 – физическая постоянная, входящая в закон, определяющий объемную плотность равновесного теплового излучения абсолютно черного тела:
Исторически закон Стефана-Больцмана был сформулирован раньше закона излучения Планка, из которого он вытекает как следствие. Закон Планка устанавливает зависимость спектральной плотности потока излучения E0 от длины волны λ и температуры T:
где λ – длина волны, м; с=2,998 10 8 м/с – скорость света в вакууме; Т – температура тела, К;
h = 6,625 ×10 -34 Дж×с– постоянная Планка.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Постоянная Больцмана
Физическая постоянная k, равная отношению универсальной газовой постоянной R=8314Дж/(кг × K) к числу Авогадро NA=6,022 × 10 26 1/(кг × моль):
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Статистика Больцмана
Число различных конфигураций системы из N частиц для данного набора чисел ni (число частиц, находящихся в i -том состоянии, которому соответствует энергия e i ) пропорционально величине:
Величина W есть число способов распределения N частиц по энергетическим уровням. Если справедливо соотношение (6) то считается, что исходная система подчиняется статистике Больцмана. Набор чисел ni , при котором число W максимально, встречается наиболее часто и соответствует наиболее вероятному распределению.
Физическая кинетика – микроскопическая теория процессов в статистически неравновесных системах.
Описание большого числа частиц может успешно осуществляться вероятностными методами. Для одноатомного газа состояние совокупности молекул определяется их координатами и значениями проекций скоростей на соответствующие координатные оси. Математически это описывается функцией распределения, характеризующей вероятность пребывания частицы в данном состоянии:
есть ожидаемое число молекул в объеме d 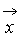
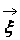
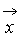
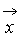
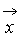
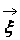
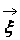
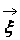
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Газ Больцмана
Если осредненной по времени потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией, то газ называется идеальным. Идеальный газ называется газом Больцмана, если отношение длины пробега молекул в этом газе к характерному размеру течения L конечно, т.е.
т.к. длина пробега обратно пропорциональна nd 2 (n – числовая плотность 1/м 3 , d – диаметр молекулы, м).
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

H-функция Больцмана
называют H-функцией Больцмана для единицы объема, которая связана с вероятностью обнаружения системы из молекул газа в данном состоянии. Каждому состоянию соответствуют определенные числа заполнения шестимерных пространственно-скоростных ячеек, на которые может быть разбито фазовое пространство рассматриваемых молекул. Обозначим W вероятность того, что в первой ячейке рассматриваемого пространства окажется N1 молекул, во второй N2 и т.д.
С точностью до постоянной, определяющей начало отсчета вероятности, правомерно соотношение:
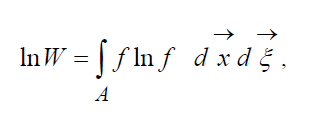
где 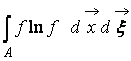
Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

H-теорема Больцмана
Видео:Атмосфера #4 | Кинетическое уравнение БольцманаСкачать

Принцип Больцмана
Больцмана принцип устанавливает связь между энтропией S физической системы и термодинамической вероятностью W её состояния:
Видео:Принцип наименьшего действия #2 - Уравнение Эйлера-ЛагранжаСкачать

Кинетическое уравнение Больцмана
(печатается по изданию: Коган М.Н. Динамика разреженного газа. – М.: Наука, 1967.)
где 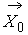
Уравнение (12) с интегралом (13) получено для столкновения молекул, при которых не возникает тангенциальных сил, т.е. сталкивающиеся частицы считаются идеально гладкими.
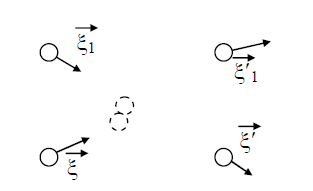
В процессе взаимодействия внутренняя энергия молекул не меняется, т.е. предполагается, что эти молекулы являются идеально упругими. Рассматриваются две группы молекул, имеющих до соударения друг с другом (столкновения) скорости 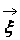
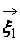
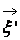
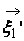
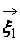
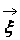
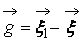
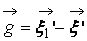
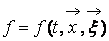
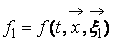
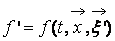
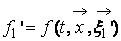
Рис. 1. Столкновение двух молекул.
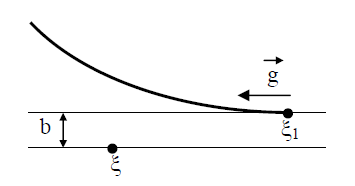
В (13) входят два параметра, характеризующие расположение сталкивающихся молекул друг относительно друга: b и ε; b – прицельное расстояние, т.е. наименьшее расстояние, на которое сблизились бы молекулы при отсутствии взаимодействия (рис. 2); ε называют угловым параметром столкновений (рис. 3). Интегрирование по b от 0 до ¥ и по от 0 до 2 p (два внешних интеграла в (12)) охватывает всю плоскость силового взаимодействия перпендикулярно вектору
Рис. 2. Траектория движения молекул.
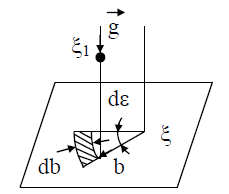
Рис. 3. Рассмотрение взаимодействия молекул в цилиндрической системе координат: z, b, ε
Кинетическое уравнение Больцмана выведено при следующих допущениях и предположениях.
1. Считается, что происходит в основном столкновения двух молекул, т.е. роль столкновений одновременно трех и большего числа молекул незначительна. Это допущение позволяет использовать для анализа одночастичную функцию распределения, которая выше названа просто функцией распределения. Учет столкновения трех молекул приводит к необходимости использования в исследовании двухчастичной функции распределения. Соответственно анализ существенно усложняется.
2. Предположение о молекулярном хаосе. Оно выражается в том, что вероятности обнаружения частицы 1 в фазовой точке 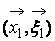
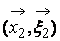
3. Равновероятны столкновения молекул с любым прицельным расстоянием, т.е. функция распределения не меняется на диаметре взаимодействия. Необходимо отметить, что анализируемый элемент 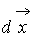
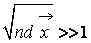

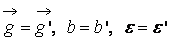
Видео:Рассмотрение темы: "Распределение Максвелла"Скачать

Распределение Максвелла-Больцмана
Равновесное состояние газа описывается абсолютным Максвелловским распределением, которое является точным решением кинетического уравнения Больцмана:
где m – масса молекулы, кг.
Общее локально-максвелловское распределение иначе называемое распределение Максвелла-Больцмана:
в том случае, когда газ движется как целое со скоростью 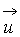
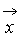
и времени t .
Видео:Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Формула Больцмана барометрическая
В поле тяготения Земли точное решение уравнения Больцмана показывает:
где n 0= плотность у поверхности Земли, 1/м 3 ; g – ускорение силы тяжести, м/с 2 ; h – высота, м. Формула (16) является точным решением кинетического уравнения Больцман либо в безграничном пространстве, либо при наличии границ, не нарушающих этого распределения, при этом температура также должна оставаться постоянной.
Эта страница оформлена Пузиной Ю.Ю. при поддержке Российского Фонда Фундаментальных Исследований – проект №08-08-00638.
Видео:Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

Уравнение больцмана для идеального газа
| Распределение Больцмана |   |
Распределение Больцмана определяет распределение частиц в силовом поле в условиях теплового равновесия.
Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает. Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов. Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P0 в барометрической формуле (2.4.1) на n и n0 и получим распределение Больцмана для молярной массы газа:
Так как
На рисунке 2.11 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.
Больцман доказал, что соотношение (2.5.3) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном поле, для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. Видео:🧬 Молекулярная физика: идеальный газ и изопроцессы с нуля | Физика ЕГЭ 2024 | УмскулСкачать  Постоянная БольцманаПостоянная Больцмана, представляющая собой коэффициент, равный k = 1 , 38 · 10 — 23 Д ж К , является частью значительного числа формул в физике. Она получила свое название по имени австрийского физика – одного из основоположников молекулярно-кинетической теории. Сформулируем определение постоянной Больцмана: Постоянной Больцмана называется физическая постоянная, с помощью которой определяется связь между энергией и температурой. Не следует путать ее с постоянной Стефана-Больцмана, связанной с излучением энергии абсолютно твердого тела. Существуют различные методы вычисления данного коэффициента. В рамках этой статьи мы рассмотрим два их них. Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать  Нахождение постоянной Больцмана через уравнение идеального газаДанная постоянная может быть найдена с помощью уравнения, описывающего состояние идеального газа. Опытным путем можно определить, что нагревание любого газа от T 0 = 273 К до T 1 = 373 К приводит к изменению его давления от p 0 = 1 , 013 · 10 5 П а до p 0 = 1 , 38 · 10 5 П а . Это достаточно простой эксперимент, который может быть проведен даже просто с воздухом. Для измерения температуры при этом нужно использовать термометр, а давления – манометр. При этом важно помнить, что количество молекул в моле любого газа примерно равно 6 · 10 23 , а объем при давлении в 1 а т м равен V = 22 , 4 л . С учетом всех названных параметров можно перейти к вычислению постоянной Больцмана k : Для этого запишем уравнение дважды, подставив в него параметры состояний. Зная результат, можем найти значение параметра k : Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать  Нахождение постоянной Больцмана через формулу броуновского движенияДля второго способа вычисления нам также потребуется провести эксперимент. Для него нужно взять небольшое зеркало и подвесить в воздухе с помощью упругой нитки. Допустим, что система зеркало-воздух находится в стабильном состоянии (статическом равновесии). Молекулы воздуха ударяют в зеркало, которое, по сути, ведет себя как броуновская частица. Однако с учетом его подвешенного состояния мы можем наблюдать вращательные колебания вокруг определенной оси, совпадающей с подвесом (вертикально направленной нитью). Теперь направим на поверхность зеркала луч света. Даже при незначительных движениях и поворотах зеркала отражающийся в нем луч будет заметно смещаться. Это дает нам возможность измерить вращательные колебания объекта. Обозначив модуль кручения как L , момент инерции зеркала по отношению к оси вращения как J , а угол поворота зеркала как φ , можем записать уравнение колебаний следующего вида: Минус в уравнении связан с направлением момента сил упругости, который стремится вернуть зеркало в равновесное положение. Теперь произведем умножение обеих частей на φ , проинтегрируем результат и получим: Следующее уравнение является законом сохранения энергии, который будет выполняться для данных колебаний (то есть потенциальная энергия будет переходить в кинетическую и обратно). Мы можем считать эти колебания гармоническими, следовательно: При выведении одной из формул ранее мы использовали закон равномерного распределения энергии по степеням свободы. Значит, можем записать так: Как мы уже говорили, угол поворота можно измерить. Так, если температура будет равна приблизительно 290 К , а модуль кручения L ≈ 10 — 15 Н · м ; » open=» φ ≈ 4 · 10 — 6 , то рассчитать значение нужного нам коэффициента можно так: Следовательно, зная основы броуновского движения, мы можем найти постоянную Больцмана с помощью измерения макропараметров. Видео:Урок 153. Распределение молекул по скоростямСкачать  Значение постоянной БольцманаЗначение изучаемого коэффициента состоит в том, что с его помощью можно связать параметры микромира с теми параметрами, что описывают макромир, например, термодинамическую температуру с энергией поступательного движения молекул: » open=» E = 3 2 k T . Этот коэффициент входит в уравнения средней энергии молекулы, состояния идеального газа, кинетической теории газа, распределение Больцмана-Максвелла и многие другие. Также постоянная Больцмана необходима для того, чтобы определить энтропию. Она играет важную роль при изучении полупроводников, например, в уравнении, описывающем зависимость электропроводности от температуры. Условие: вычислите среднюю энергию молекулы газа, состоящего из N -атомных молекул при температуре T , зная, что у молекул возбуждены все степени свободы – вращательные, поступательные, колебательные. Все молекулы считать объемными. Энергия равномерно распределяется по степеням свободы на каждую ее степень, значит, на эти степени будет приходиться одинаковая кинетическая энергия. Она будет равна » open=» ε i = 1 2 k T . Тогда для вычисления средней энергии мы можем использовать формулу: » open=» ε = i 2 k T , где i = m p o s t + m υ r + 2 m k o l представляет собой сумму поступательных вращательных степеней свободы. Буквой k обозначена постоянная Больцмана. Переходим к определению количества степеней свободы молекулы: m p o s t = 3 , m υ r = 3 , значит, m k o l = 3 N — 6 . i = 6 + 6 N — 12 = 6 N — 6 ; » open=» ε = 6 N — 6 2 k T = 3 N — 3 k T . Ответ: при данных условиях средняя энергия молекулы будет равна » open=» ε = 3 N — 3 k T . Условие: есть смесь двух идеальных газов, плотность которых в нормальных условиях равна p. Определите, какова будет концентрация одного газа в смеси при условии, что мы знаем молярные массы обоих газов μ 1 , μ 2 . Сначала вычислим общую массу смеси. m = ρ V = N 1 m 01 + N 2 m 02 = n 1 V m 01 + n 2 V m 02 → ρ = n 1 m 01 + n 2 m 02 . Параметр m 01 обозначает массу молекулы одного газа, m 02 – массу молекулы другого, n 2 – концентрацию молекул одного газа, n 2 – концентрацию второго. Плотность смеси равна ρ . Теперь из данного уравнения выразим концентрацию первого газа: n 1 = ρ — n 2 m 02 m 01 ; n 2 = n — n 1 → n 1 = ρ — ( n — n 1 ) m 02 m 01 → n 1 = ρ — n m 02 + n 1 m 02 m 01 → n 1 m 01 — n 1 m 02 = ρ — n m 02 → n 1 ( m 01 — m 02 ) = ρ — n m 02 . Далее нам потребуется уравнение, описывающее состояние идеального газа: p = n k T → n = p k T . Подставим полученное равнее значение: n 1 ( m 01 — m 02 ) = ρ — p k T m 02 → n 1 = ρ — p k T m 02 ( m 01 — m 02 ) . Поскольку молярные массы газов нам известны, мы можем найти массы молекул первого и второго газа: m 01 = μ 1 N A , m 02 = μ 2 N A . Также мы знаем, что смесь газов находится в нормальных условиях, т.е. давление равно 1 а т м , а температура 290 К . Значит, мы можем считать задачу решенной. Ответ: в данных условиях рассчитать концентрацию одного из газов можно как n 1 = ρ — p k T m 02 ( m 01 — m 02 ) , где m 01 = μ 1 N A , m 02 = μ 2 N A . 🔍 ВидеоРешение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать  Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать  |
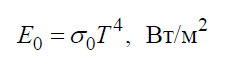
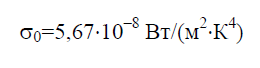
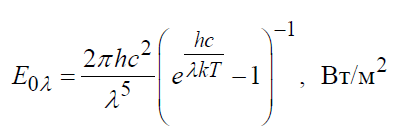
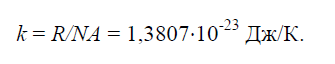
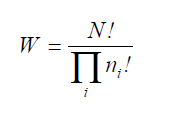
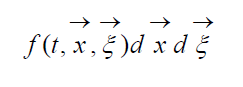
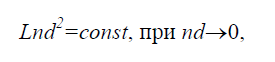
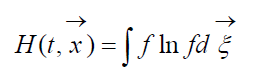
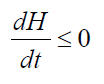
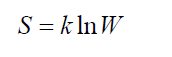
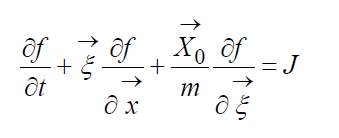
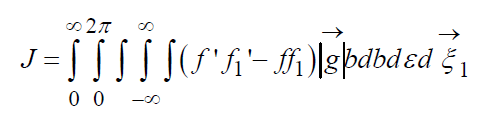
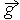
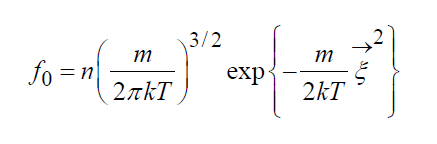
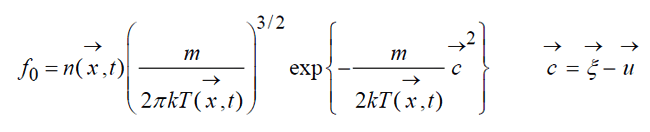
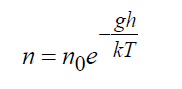



 а
а  , то (2.5.1) можно представить в виде
, то (2.5.1) можно представить в виде
 ,
, .
.