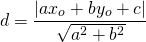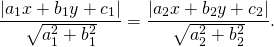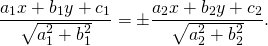Уравнение биссектрисы угла между прямыми на плоскости (3 видео)

Уравнение биссектрисы угла

Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.

Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0.

Расстояние от точки (x_o;y_o) до прямой ax+by+c=0 определяется по формуле

По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

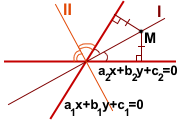
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0, находится от этих прямых на одинаковом расстоянии, то есть

Это равенство можно записать в виде

Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.

Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.

В формулу уравнения биссектрис подставляем данные прямых:

Содержание

Составить уравнение биссектрис углов образованных двумя прямыми
Что ты хочешь узнать?
Ответ
Проверено экспертом
Задача 34288 Составить уравнение биссектрисы угла.
Условие
Решение
🎬 Видео

Видео:найти уравнения биссектрис углов между прямымиСкачать

Составить уравнение биссектрис углов образованных двумя прямыми

Составить уравнение биссектрисы острого угла между прямыми

Решение

Найдем точку пересечения двух прямых

Направляющий вектор первой прямой есть , второй , так как их скалярное произведение положительно , поэтому найдем уравнение биссектрисы между векторами , проходящую через точку

Направляющий вектор биссектрисы угла равен сумме нормированных направляющих векторов сторон

Так как точка лежит на этой биссектрисе, то

Задание 8

Составить уравнение плоскости, которая проходит через точку параллельно плоскости

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9987 – | 7776 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.

Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0.

Расстояние от точки (x_o;y_o) до прямой ax+by+c=0 определяется по формуле

По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

Это равенство можно записать в виде

Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.

Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.

В формулу уравнения биссектрис подставляем данные прямых:

Что ты хочешь узнать?

Видео:Видеоурок "Угол между прямыми"Скачать

Ответ

Проверено экспертом

Даны прямые: 11x-2y+5=0 и 4x+8y-7=0

Уравнения биссектрис углов между прямыми Ax + By + C = 0 и A₁x + B₁y + C₁ = 0:

Знак + или – выбирается в зависимости от того, нужно уравнение биссектрисы острого или тупого углов.

Подставив коэффициенты заданных прямых в приведенную формулу, получим уравнения биссектрис:

В приближённом варианте у ≈ 1,3541х + 1,3772.

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Задача 34288 Составить уравнение биссектрисы угла.

Условие

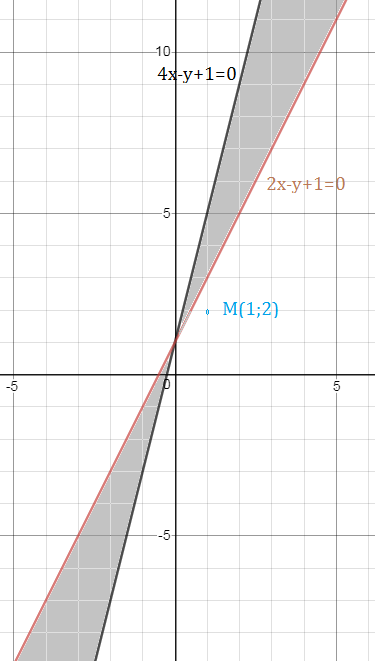
Составить уравнение биссектрисы угла между прямыми l1(4x–y+1=0) и l2(2x–y+1=0) смежного с углом, содержащим точку M(1;2)

Решение

Пусть точка Р(х;у) лежит на биссектрисе угла между прямыми.
Это значит, что расстояние d_(1) это точки до прямой l_(1) равно
расстоянию d_(2) это точки до прямой l_(2)

Прямая 4x–y+1=0 разбивает плоскость хОу на две области:
4x–y+1>0 или 4x–y+1 0 — верно;
Прямая 2x–y+1=0 разбивает плоскость хОу на две области:
2x–y+1>0 или 2x–y+1 0 — верно;

Значит точка M принадлежит области
4x–y+1>0
2x–y+1>0
а смежные области задаются неравенствами противоположных знаков.

Поэтому в (#) знак модуля раскрывается так:
(4x-y+1)/sqrt(4^2+1^2) =- (2x-y+1)/sqrt(2^2+1^2)

Делим на (sqrt(5)+sqrt(17))

((2sqrt(17)+4sqrt(5))/(sqrt(17)+sqrt(5))) * x — y + 1=0

Избавляемся от иррациональности в знаменателе

[b]((7 — sqrt(85))/6)*x — y + 1 = 0[/b]