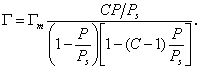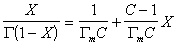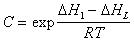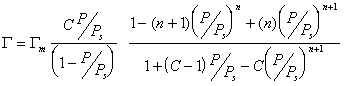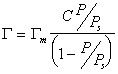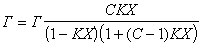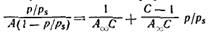Уравнение бэт и его применение (5 видео)

Уравнение бэт и его применение

В большинстве случаев реальная поверхность твердого тела не вполне однородна энергетически; адсорбция, как правило, не является строго локализованной; адсорбированные молекулы практически всегда взаимодействуют между собой; наконец, стехиометрия может нарушаться, вследствие чего адсорбция не будет ограничена образованием одного слоя. Поэтому реальные изотермы адсорбции всегда отклоняются от изотермы Ленгмюра. Еще самим Ленгмюром было показано, что если адсорбционные центры считать энергетически неоднородными, то суммарная адсорбция на всех центрах будет выражена следующим уравнением:

где i — количество групп одинаковых центров.

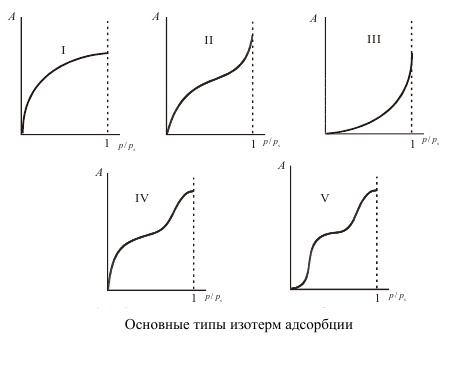
Брунауэр, Эммет и Теллер отказались от второго допущения Ленгмюра, приводящего к мономолекулярной адсорбции. Для случая, когда температура адсорбтива ниже критической (то есть, это еще пар) они разработали теорию полимолекулярной адсорбции. После анализа многочисленных реальных изотерм адсорбции ими была предложена их классификация на основе выделения пяти основных типов изотерм.

Изотермы типа I отражают мономолекулярную адсорбцию. Изотермы типа II и III обычно связывают с образованием при адсорбции многих слоев, то есть, с полимолекулярной адсорбцией. Приче м, в случае II взаимодействие адсорбент — адсорбат сильнее взаимодействия адсорбат — адсорбат, а в случае III — наобор от. Изотермы типа IV и V отличаются тем, что для них характерна конечная адсорбция при приближении давления пара к давлению насыщения p_s. Изотермы типа II и III характерны для адсорбции на не пористом адсорбенте, а типа IV и V — на пористом твердом теле. Все пять типов изотерм адсорбции описываются теорией полимолекулярной адсорбции “БЭТ”, названной так по начальным буквам фамилий ее авторов.

Теория БЭТ сохраняет ленгмюровские представления о динамическом характере адсорбции. Адсорбция считается полислойной. Молекулы первого слоя адсорбируются на поверхности адсорбента в результате межмолекулярного взаимодействия адсорбент — адсорбат. Каждая адсорбированная молекула первого адсорбционного слоя может, в свою очередь, являться центром адсорбции молекул второго слоя и т.д. Так формируются второй и последующие сорбционные слои. Теплота адсорбции в первом слое q₁ определяется взаимодействием адсорбат — адсорбент, во всех последующих слоях — взаимодействием адсорбат — адсорбат. Поэтому теплота адсорбции во всех слоях, начиная со второго, равна теплоте конденсации λ. Второй и последующие адсорбционные слои могут начинать образовываться и при незавершенном первом слое, как это показано на рисунке:

Составив уравнение адсорбционного равновесия для каждого слоя и просуммировав их, авторы теории БЭТ получили уравнение для полислойной адсорбции:

В приведенном уравнении А_М — емкость монослоя, С — константа, равная е (q1− λ) / RT . При малых относительных давлениях, когда р как частный случай уравнения БЭТ. В случаях, когда q₁ > λ , т.е. энергия взаимодействия адсорбент — адсорбат больше энергии взаимодействия адсорбат — адсорбат, изотерма адсорбции выпукла и относится к типу II или IV. Если же энергия взаимодействия адсорбат — адсорбат больше теплоты адсорбции ( λ > q₁ ), то изотерма адсорбции вогнута и относится к типу III или V.

Уравнение изотермы адсорбции БЭТ широко используется для определения величины удельной поверхности адсорбентов. Изотерма адсорбции выражается прямой линией, отсекающей на оси ординат отрезок, равный 1 / А_М С , а тангенс угла ее наклона к оси абсцисс равен (С − 1) / А_М С.

Из этих значений можно найти величину А_М, а зная ее, рассчитать по уравнению удельную поверхность адсорбента. Стандартной методикой для определения удельной поверхности адсорбентов принято считать измерение изотермы адсорбции азота при 77 К. В этом случае w_о = 0.162 нм 2 .

Источник: Пальтиель Л.Р., Зенин Г.С., Волынец Н.Ф. КОЛЛОИДНАЯ ХИМИЯ: Учеб. пособие. – СПб: СЗТУ, 2004. – 68 с.
Источник: Кукушкина И.И., Митрофанов А.Ю. Коллоидная химия, Кемерово:2009 — 185 с.

Видео:5.1. Адсорбция. Классификация адсорбцииСкачать

Метод БЭТ

Метод БЭТ сокр., БЭТ (англ. BET) — метод математического описания физической адсорбции основанный на теории полимолекулярной (многослойной) адсорбции.

Теория полимолекулярной адсорбции была развита в работах Брунауэра, Эммета и Теллера (БЭТ). В основе этой теории лежит распространение обобщенных представлений локализованного монослоя на полислойную адсорбцию. В теории БЭТ используется предпосылка, что молекулы каждого предыдущего адсорбционного слоя служат активными центрами при образовании последующих слоев. Это предполагает, что емкость каждого слоя одинакова. Считается, что силами взаимодействия между молекулами в каждом адсорбционном слое можно пренебречь (отсутствие латеральных взаимодействий), а молекулы каждого адсорбционного слоя локализованы. Полагается, что адсорбционный потенциал в первом адсорбционном слое значительно выше, чем в других слоях, а начиная со второго адсорбционного слоя он сопоставим с энергией конденсации (изотермы типа II, IV) или для всех слоев одинаков (изотермы III, IV).

Существует несколько методик вывода уравнений изотермы полимолекулярной адсорбции. В работах Брунауэра с сотрудниками использовался кинетический вывод уравнения изотермы полимолекулярной адсорбции. Позднее вывод этого уравнения был осуществлен методом статистической термодинамики.

В оригинальном кинетическом выводе уравнения изотермы адсорбции БЭТ рассматривается равновесие между адсорбционными комплексами различного заполнения. Считается, что на поверхности адсорбента одновременно могут находиться незаполненные активные центры и адсорбционные комплексы, содержащие 1, 2, 3…i, молекул адсорбата, которым соответствует площадь поверхности адсорбентаA0, A1, A2, A3, …Ai.

В 1937 году Брунауэр С., Эммет П. и Теллер Е. вывели уравнение полимолекулярной физической адсорбции, которое описывает зависимость физической адсорбции от величины поверхности:

Уравнение известно как простая форма изотермы адсорбции БЭТ. Это уравнение может быть представлено в линейной форме. Обозначим для упрощения Р/Р S =Х и разделим на X обе части уравнения:

В такой форме график зависимости должен давать прямую с наклоном С-1/Г_mС и отрезком, отсекающим на оси ординат 1/ Г_mС .Решение двух численных уравнений позволяет определить постоянную уравнения С, предел адсорбции Г_m в монослое и рассчитать удельную активную поверхность А_уд = n_mA_o = Г_mA_oN_A, где Г_m должна быть выражена в моль/г; А₀– называют площадью молекулярного сечения адсорбата или чаще – адсорбционной «посадочной площадкой» (этот параметр представляет собой площадь, которую занимает молекула адсорбата в насыщенном мономолекулярном слое).

Температурная зависимость постоянных равновесия K₁ и С позволяет определить чистую теплоту адсорбции, так как

где DH1 , DHL – теплота адсорбции в первом адсорбционном слое и теплота конденсации адсорбата.

Если адсорбент пористый и адсорбция идет в результате заполнения мезопор, то уравнение БЭТ принимает вид:

Интересно отметить, что уравнение при n=1 переходит в уравнение Ленгмюра:

В то время как уравнение БЭТ в простейшей форме может перейти в уравнение Ленгмюра только при дополнительных условиях, что С>>1 и Р/Р_s 2, то уравнение БЭТ дает изотермы типа II, при С

Строго говоря, достаточно надежные данные по емкости монослоя получаются лишь при обработке результатов эксперимента по адсорбции в области малых давлений, где модель полислойной адсорбции БЭТ оказывается справедливой. Часто на линейной изотерме адсорбции наблюдаются два участка – один в области низких относительных давлений, другой — при более высоких давлениях. Для расчетов Г_m следует использовать линейный участок при низких давлениях, но только в том случае, если он включает в себя точку В. Чаще всего для определения емкости монослоя используют данные по адсорбции при 0,05 0,3 проявляется латеральное взаимодействие в адсорбционных споях.

Статистико-механическая трактовка полимолекулярной адсорбции и соответствующий вывод уравнения изотермы не позволяют снять указанные выше ограничения.

Кроме того, предпринимались неоднократные попытки модифицировать уравнение БЭТ. Так Андерсон предположил, что от второго до примерно девятого слоев теплота адсорбции отличается от теплоты конденсации на некоторую постоянную величину. Это позволило ввести в простейшее уравнение некоторую постоянную K

Интересно отметить, что в более поздних работах Брунауэра была получена аналогичная форма уравнения, но вывод его был основан на другой модели, а именно, на предпосылке, что число адсорбционных слоев даже на открытой поверхности при давлении насыщения Р/Рs®1 ограничено (5-6). Такое допущение также noзволяет ввести коэффициент K 2 /г, включив в нее изотерму адсорбции на природном кварце и различных образцах непористого и аморфного кремнезема. Такие стандартные изотермы получены и для других систем.

Многочисленные эксперименты на непористых сорбентах показали, что для определения удельной поверхности твердых адсорбентов наиболее удобно простейшее уравнение БЭТ. Для таких целей используют азот, аргон и криптон. Последний, предпочтительнее для адсорбентов с малой величиной удельной активной поверхности.

Видео:Практическое занятие 5. Уравнение БЭТ. Удельная поверхностьСкачать

Экзаменационный билет № 10

Уравнение Ленгмюра можно использовагь только при условии, что адсорбция вещества сопровождается образованием мономолекулярного слоя.

В большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и влияние поверхностных сил может распространяться на второй, третий и последующие адсорбционные слои, в результате проходит полимолекулярная адсорбция.

Современная форма уравнения полимолекулярной адсорбции — основного уравнения обобщенной теории Ленгмюра — была предложена Брунауэром, Эмметом и Теллером.

В этой теории дополнительным допущением к тем, которые были положены в основу вывода уравнения изотермы Ленгмюра, является представление об образовании на поверхности адсорбента «последовательных комплексов» адсорбционных центров с одной, двумя, тремя и т. д. молекулами адсорбата. Тогда процесс адсорбции можно представить в виде последовательных квазихимических реакций:

Константы равновесия этих реакций соответственно равны

Обозначим:

Общее число активных центров на адсорбенте, или емкость монослоя, будет равна

После ряда вычислений с применением теории рядов, окончательно получим:

Данное соотношение является основным уравнением обобщенной теории Ленгмюра и называется уравнением полимолекулярной адсорбции БЭТ.

При обработке экспериментальных результатов уравнение БЭТ обычно используют в линейной форме:

Оно позволяет графически определить оба постоянных параметра A_∞ и С:

Экспериментальное определение A_∞ позволяет рассчитать удельную поверхность адсорбента (поверхность единицы массы адсорбента): .

Лиофильные дисперсные системы. Истинно растворимые и коллоидные ПАВ, их классификация. Мицеллообразование, строение мицелл, методы определения ККМ. Факторы, влияющие на ККМ.

Все дисперсные системы в зависимости от механизма процесса их образования по классификации П. А. Ребиндера подразделяют на лиофильные, которые получаются при самопроизвольном диспергировании одной из фаз (самопроизвольное образование гетерогенной свободнодисперсной системы), и лиофобные, получающиеся в результате диспергирования и конденсации с пересыщением (принудительное образование гетерогенной свободноднсперсной системы).

Наличие гидрофильной и олеофильной частей у молекул ПАВ является характерной отличительной особенностью их строения. По способности к диссоциации в водных растворах поверхностно-активные вещества делят на ионогенные и неионогенные. В свою очередь ионогенные ПАВ подразделяют на анионные, катионные и амфолитпые (амфотерные).

1) Анионные ПАВ диссоциируют в воде с образованием поверхностно-активного аниона.

2) Катионные ПАВ диссоциируют в воде с образованием поверхностно-активного катиона.

3) Амфолитные ПАВ содержат две функциональные группы, одна из которых имеет кислый, а другая основный характер, например карбоксильную и аминную группы. В зависимости от рН среды амфолитные ПАВ проявляют анионоактивные или катионоактивные свойства.

Все ПАВ относительно поведения их в воде делят на истинно растворимые и коллоидные.

Истинно растворимые ПАВ в растворе находятся в молекулярно-дисперсном состоянии вплоть до концентраций, соответствующих их насыщенным растворам и разделению системы на две сплошные фазы.

Главной отличительной особенностью коллоидных ПАВ является способность образовывать термодинамически устойчивые (лиофильные) гетерогенные дисперсные системы (ассоциативные, или мицеллярные, коллоиды). К основным свойствам коллоидных ПАВ, обусловливающим их ценные качества и широкое применение, относятся высокая поверхностная активность; способность к самопроизвольному мицеллообразованию — образованию лиофильных коллоидных растворов при концентрации ПАВ выше некоторого определенного значения, называемого критической концентрацией мицеллообразования (KKM); способность к солюбилизации — резкому увеличению растворимости веществ в растворах коллоидных ПАВ вследствне их «внедрения» внутрь мицеллы; высокая способность стабилизировать различные дисперсные системы.

При концентрациях выше KKM молекулы ПАВ собираются в мицеллы (ассоциируют) и раствор перехолит в мицеллярную (ассоциативную) коллоидную систему.

Под мицеллой ПАВ понимают ассоциат дифильных молекул, лиофильные группы которых обращены к соответствующему растворителю, а лиофобные группы соединяются друг с другом, образуя ядро мицеллы. Число молекул, составляющих мицеллу, называют числом ассоциации, а общую сумму молекулярных масс молекул в мицелле, или произведение массы мицеллы на число Авогадро, — мицеллярной массой. Определенное ориентирование дифильных молекул ПАВ в мицелле обеспечивает минимальное межфазное натяжение на границе мицелла — среда.

При концентрациях ПАВ в водном растворе, несколько превышающих KKM, согласно представлениям Гартли образуются сферические мицеллы (мицеллы Гартли). Внутренняя часть мицелл Гартли состоит из переплетающихся углеводородных радикалов, полярные группы молекул ПАВ обращены в водную фазу. Диаметр таких мицелл равен удвоенной длине молекул ПАВ. Число молекул в мицелле быстро растет в пределах узкого интервала концентраций, а при дальнейшем увеличении концентрации практически не изменяется, а увеличивается число мицелл. Сферические мицеллы могут содержать от 20 до 100 молекул и более.

При увеличении концентрации ПАВ мицеллярная система проходит ряд равновесных состояний, различающихся по числам ассоциации, размерам и форме мицелл. При достижении определенной концентрации сферические мицеллы начинают взаимодействовать между собой, что способствует их деформации. Мицеллы стремятся принять цилиндрическую, дискообразную, палочкообразную, пластинчатую форму.

Мицеллообразование в неводных средах, как правило, является результатом действия сил притяжения между полярными группами ПАВ и взаимодействия углеводородных радикалов с молекулами растворителя. Образующиеся мицеллы обращенного вида содержат внутри негидратированные или гидратированные полярные группы, окруженные слоем из углеводородных радикалов. Число ассоциации (от 3 до 40) значительно меньше, чем для водных растворов ПАВ. Как правило, оно растет с увеличением углеводородного радикала до определенного предела.

Критическая концентрация мицеллообразования — важнейшая характеристика растворов ПАВ. Она зависит прежде всего от строения углеводородного радикала в молекуле ПАВ и характера полярной группы, наличия в растворе электролитов и неэлектролитов, температуры и других факторов.

Факторы, влияющие на ККМ:

1) При увеличении длины углеводородного радикала повышается растворимость ПАВ и возрастает KKM. Разветвленность, непредельность и циклизация углеводородного радикала уменьшают склонность к мицеллообразованию и увеличивают KKM. Характер полярной группы играет существенную роль при мицеллообразовании в водных и неводных средах.

2) Введение электролитов в водные растворы неионогенных ПАВ слабо влияет на KKM и размер мицеллы. Для ионогенных ПАВ это влияние существенно.

3) Введение неэлектролитов (органических растворителей) в водные растворы ПАВ также приводит к изменению KKM.

Методы определения KKM основаны на регистрации резкого изменения физико-химических свойств растворов ПАВ в зависимости от концентрации (например, поверхностного натяжения σ, мутности τ, эквивалентной электропроводности λ, осмотического давления π, показателя преломления n). На кривой зависимости свойство — состав в области KKM обычно появляется излом.

1) Кондуктометрический метод применяется для определения KKM ионогенных ПАВ.

2) Другой метод’ определения KKM основан на измерении поверхностного натяжения водных растворов ПАВ, которое резко уменьшается с ростом концентрации вплоть до KKM, а затем остается постоянным.

3) Солюбилизация красителей и углеводородов в мицеллах позволяет определять KKM ионогенных и неионогенных ПАВ как в водных, так и неводных растворах. При достижении в растворе ПАВ концентрации, соответствующей KKM, растворимость углеводородов и красителей резко увеличивается.

4) Измерение интенсивности светорассеяния при мицеллообразовании позволяет не только находить KKM по резкому увеличению наклона концентрационной кривой, но и опоеделять мицеллярную массу и числа ассоциации.