Уравнение бернулли и подъемная сила самолета (6 видео)

Содержание

Школьная Энциклопедия
Nav view search
Навигация
Искать
Закон Бернулли в аэродинамике
Уравнение неразрывности струи
Уравнение Бернулли
Парадокс шмеля, или Трактат О подъёмной силе
Почему и как возникает подъемная сила
Возникновение подъемной силы
🔥 Видео

Видео:Подъёмная сила крыла ● 1Скачать

Школьная Энциклопедия

Видео:Как летает самолет? Закон Бернулли - Основы авиации #2Скачать

Nav view search

Искать

Видео:Подъемная сила крылаСкачать

Закон Бернулли в аэродинамике

Подробности Категория: Человек и небо Опубликовано 23.07.2014 16:59 Просмотров: 25060

Какое отношение к авиации имеет закон Бернулли? Оказывается, самое прямое. С его помощью можно объяснить возникновение подъёмной силы крыла самолёта и других аэродинамических сил.

Автор этого закона — швейцарский физик-универсал, механик и математик. Даниил Бернулли — сын известного швейцарского математика Иоганна Бернулли. В 1838 г. он опубликовал фундаментальный научный труд «Гидродинамика», в котором и вывел свой знаменитый закон.

Следует сказать, что в те времена аэродинамика как наука ещё не существовала. А закон Бернулли описывал зависимость скорости потока идеальной жидкости от давления. Но в начале ХХ века начала зарождаться авиация. И вот тут закон Бернулли оказался очень кстати. Ведь если рассматривать воздушный поток как несжимаемую жидкость, то этот закон справедлив и для воздушных потоков. С его помощью смогли понять, как поднять в воздух летательный аппарат тяжелее воздуха. Это важнейший законом аэродинамики, так как он устанавливает связь между скоростью движения воздуха и действующим в нём давлением, что помогает делать расчёты сил, действующих на летательный аппарат.

Закон Бернулли — это следствие закона сохранения энергии для стационарного потока идеальной и несжимаемой жидкости.

В аэродинамике воздух рассматривается как несжимаемая жидкость, то есть, такая среда, плотность которой не меняется с изменением давления. А стационарным считается поток, в котором частицы перемещаются по неизменным во времени траекториям, которые называют линиями тока. В таких потоках не образуются вихри.

Чтобы понять сущность закона Бернулли, познакомимся с уравнением неразрывности струи.

Уравнение неразрывности струи

Если жидкость течёт по трубе, имеющей разное поперечное сечение, то давление в разных местах трубы будет неодинаковое.

Мысленно выделим в трубе несколько сечений, обозначив их площади S₁ и S₂. Соответственно, v₁ и v₂ – скорости течений несжимаемой жидкости через эти сечения.

За время ∆t через сечения протекут жидкости, объёмы которых будут равны:

Так как мы рассматриваем стационарное течение несжимаемой жидкости, то по закону сохранения массы через любое поперечное сечение трубы за одинаковый промежуток времени проходит одинаковый объём жидкости. Следовательно, ∆V₁ = ∆V₂.

Произведение площади поперечного сечения потока на его скорость есть величина постоянная. Это уравнение называют уравнением неразрывности струи.

Уравнение Бернулли

Объединив условие неразрывности жидкости и закон сохранения энергии, Бернулли вывел уравнение, согласно которому с увеличение скорости потока уменьшается давление, и наоборот.

То есть, скорости жидкостей обратно пропорциональны площадям сечений. И чем больше площадь сечения, тем меньше скорость жидкости, протекающей через него, и наоборот.

Подобное явление мы видим, когда стоим на берегу реки и наблюдаем за её течением. В узком месте русла скорость течения воды всегда больше, чем в широком.

Жидкость, поступающая из широкой в более узкую часть трубы, ускоряется. Это означает, что на неё действует сила со стороны жидкости, находящейся в более широкой части трубы. Откуда же берётся эта сила? Для горизонтальной трубы причина возникновения этой силы — разность давлений в широком и узком участках трубы. В широкой части давление выше, чем в узкой, а скорость ниже. Отсюда следует вывод: «При стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и наоборот».

Уравнение Бернулли имеет вид:

где ρ – плотность жидкости,

ν – скорость потока,

h – высота, на которой располагается элемент жидкости,

ɡ — ускорение свободного падения,

p – давление в точке пространства, в которой расположен центр массы элемента жидкости.

Первое слагаемое уравнения Бернулли – кинетическая энергия потока, или динамическое давление. Его создаёт движение жидкости или газа. В авиации его также называют скоростным напором.

Второе слагаемое — потенциальная энергия, или гидростатическое давление. Оно создаётся весом столба жидкости или газа высотой h.

И, наконец, третье слагаемое, Р – это статистическое давление, которое оказывают друг на друга соседние слои жидкости или газа.

Сумма всех слагаемых уравнения называется полным давлением.

Для трубы, расположенной горизонтально, или горизонтального воздушного потока уравнение Бернулли выглядит так:

Из него видно, что чем выше скорость течения жидкости (а в аэродинамике – скорость воздушного потока), тем меньше давление, и наоборот.

Эффект Бернулли можно наблюдать, сидя у камина. Во время сильных порывов ветра скорость воздушного потока возрастает, а давление падает. В комнате давление воздуха выше. И языки пламени устремляются вверх в дымоход.

Закон Бернулли и авиация

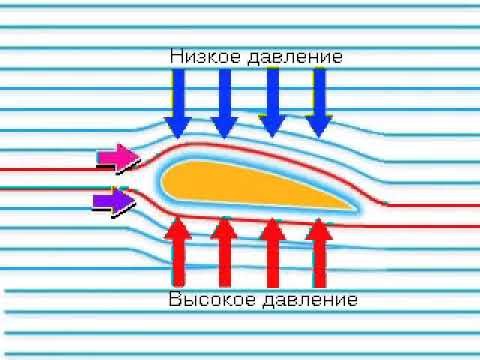
С помощью этого закона очень просто объяснить, как возникает подъёмная сила для летательного аппарата тяжелее воздуха.

Во время полёта крыло самолёта как бы разрезает воздушный поток на две части. Одна часть обтекает верхнюю поверхность крыла, а другая нижнюю. Форма крыла такова, что верхний поток должен преодолеть больший путь для того, чтобы соединиться с нижним в одной точке. Значит, он двигается с большей скоростью. А раз скорость больше, то и давление над верхней поверхностью крыла меньше, чем под нижней. За счёт разности этих давлений и возникает подъёмная сила крыла.

Во время набора самолётом высоты возрастает разница давлений, а значит, увеличивается и подъёмная сила, что позволяет самолёту подниматься вверх.

Сразу сделаем уточнение, что вышеописанные законы действуют, если скорость движения воздушного потока не превышает скорость звука (до 340 м/с). Ведь мы рассматривали воздух как несжимаемую жидкость. Но оказывается, что при скоростях выше скорости звука воздушный поток ведёт себя по-другому. Сжимаемостью воздуха пренебрегать уже нельзя. И воздух в этих условиях, как любой газ, старается расшириться и занять больший объём. Появляются значительные перепады давления или ударные волны. А сам воздушный поток не сужается, а, наоборот, расширяется. Решением задач о движении воздушных потоков со скоростями, близкими или превышающими скорость звука, занимается газовая динамика, возникшая как продолжение аэродинамики.

Используя аэродинамические законы, теоретическая аэродинамика позволяет сделать расчёты аэродинамических сил, действующих на летательный аппарат. А правильность этих расчётов проверяют, испытывая построенную модель на специальных экспериментальных установках, которые называются аэродинамическими трубами. Эти установки позволяют измерить величину сил специальными приборами.

Кроме исследования сил, действующих на аэродинамические модели, с помощью аэродинамических измерений изучают распределение значений скорости, плотности и температуры воздуха, обтекающего модель.

Видео:Аэродинамика для всех - Часть 2 Закон Бернулли, Угол атакиСкачать

Парадокс шмеля, или Трактат О подъёмной силе

Теоретическую аэродинамику не понимает даже тот, кто её преподаёт. К такому выводу пришли математики из NASA, когда попытались по примеру британских учёных рассчитать подъёмную силу конкретного крыла, используя для этого хорошее знание законов математической физики. И оказалось: всё, что летает, делает это против всех законов ньютоновской физики, так как вычисленная ими подъёмная сила всегда была очень мала по отношению к весу летательного аппарата или божьей твари. Так появился известный «парадокс шмеля». Но если математик утверждает, что шмель не должен летать, то он просто не то считает; если физик утверждает то же самое, то он — математик. Не волнуйтесь, мы этот парадокс решим, только сначала вспомним основоположников.

Леонардо да Винчи (1452-1519) открыл будущим авиаконструкторам принцип пропорциональности: подъёмная сила пропорциональна площади несущих поверхностей. При этом сам он думал так: дескать, если пропорции, скажем, комара увеличить до масштаба тела человека, то получится человек-комар, и он, скорее всего, полетит. Сам принцип пропорциональности до сих пор используется при создании совершенно новых самолётов. И работает он так: сначала конструкторы делают небольшую модель и испытывают её в аэродинамической трубе; потом – небольшой самолёт-аналог; и только потом – самолёт-прототип. Принцип пропорциональности Леонардо да Винчи следовало бы знать всем тем чудакам, что прыгали с Эйфелевой башни с крохотными крылышками за спиной.

Александр Можайский (1825-1890) установил, что подъёмная сила крыла пропорциональна его площади, его углу наклона к вектору движения, его скорости и плотности воздуха. Все эти четыре фактора он объединил и назвал одним термином – «лобовое сопротивление». Причём ни у его воздушного змея, на котором он «дважды поднимался в небо и летал с комфортом», ни у его модели самолёта, действовавшей от часовой пружины и перевозившей по воздуху офицерский кортик, ни у «самолёта Можайского» ещё не было настоящих крыльев.

У настоящего крыла, как известно, всегда две аэродинамические поверхности – нижняя и верхняя. Можайский был теоретиком только нижней и плоской поверхности атакующего крыла, а Альберт Эйнштейн — только верхней горбатой поверхности неатакующего крыла. Для объяснения возникновения подъёмной силы крыла Эйнштейн применил своё понимание закона Бернулли: мол, чем больше скорость обтекающего горб потока, тем меньше его атмосферное давление на поверхность крыла.

Николай Жуковский полагал, что большой продольный горб способствует образованию «присоединённых вихрей», которые толкают крыло снизу вверх. Самолёт Жуковского был кем-то назван «шестикрылым монстром доаэродинамического периода», а самолёт Эйнштейна его испытатель Пауль Георг Эрхард (1889-1961) сравнил с беременной уткой. Самолёт Жуковского («КОМТА») и самолёт Эйнштейна не полетели по банальной причине — очень большого паразитного лобового сопротивления горбатых крыльев. Трудов Можайского эти математики, очевидно, не читали, а совершенно плоского воздушного змея с хвостом из мочала не видели и в глаза. Однако именно они и являются основоположниками теоретической или математической аэродинамики горбатых крыльев, которую уже никто не понимает.

Специалисты NASA сразу признали теорию «присоединённых вихрей» Жуковского «нефизической», так как никакие вихри не «присоединяются» под крылом самолёта и не создают подъёмную силу. Объяснение Эйнштейном подъёмной силы через различную скорость обтекания несимметричного профиля и известный закон Бернулли они вообще признали «нелогичным», так как сам Эйнштейн и под дулом пистолета не смог бы объяснить увеличение подъёмной силы при разгоне самолёта, ведь оба потока – верхний и нижний – ускоряются при этом совершенно одинаково, а закон Бернулли действует и сверху, и снизу крыла. Таким образом, ими было принято только объяснение Александра Фёдоровича Можайского – «подъёмная сила плоского крыла равна его лобовому сопротивлению при положительных углах атаки». Говорят, к этом же выводу пришёл когда-то ещё сам Ньютон.

«Плотность среды» в формуле Можайского спецы из NASA заменили на «массовая плотность среды», что и позволило им вычислять подъёмную силу через массу воздуха, отбрасываемого атакующим крылом, и законы Ньютона. Если один куб. метр воздуха весит 1225 г, действие всегда равно противодействию, а сила – это масса, умноженная на ускорение в квадрате, то масса воздуха, вытесненного атакующим крылом из объёмной дыры, пробиваемой им в массиве воздуха за одну секунду, помноженная на ускорение, — это и есть искомая подъёмная сила. Такой была логистика их решения, а вычисленная ими подъёмная сила оказалась меньше веса самолёта примерно в 6 раз. И это, знаете ли, просто детский сад, ведь вектор действия силы лобового сопротивления всегда направлен чуть ли не строго против вектора движения самолета и вектора тяги. Однако любой математик всегда начинает считать, не успев подумать, а знание математики делает его ещё глупее, чем он есть на самом деле. («Занимаясь расчётами, ты попадаешь впросак прежде, чем успеваешь это осознать» (Эйнштейн). но чаще этого не замечаешь.

Мы «плотность среды» и «массовая плотность среды» в формуле Можайского заменим на «упругая плотность среды» и решим «парадокс шмеля» проще простого. «Упругость газов равна давлению в них» (М.В. Ломоносов). Вот через разницу атмосферного давления на нижнюю и верхнюю поверхности крыла мы и найдём искомую подъёмную силу.

Атмосферное давление на уровне моря даже несколько больше 1 кг/см2. К примеру, для орла весом в 4 кг, имеющего «площадь несущих поверхностей» 1 м2 и почти неподвижно парящего в воздухе, минимальная положительная разница атмосферного давления на обе поверхности крыла равна всего 0,4 г/см2, то есть всего 0,04 процента от теоретически возможной разницы атмосферного давления на верхнюю и нижнюю поверхность крыла в 1000 г/см2. Что тут сложного и что тут невозможного. Шмель может летать при положительной разнице атмосферного давления, скажем, 0,5 г на каждый квадратный сантиметр его крыльев. А современные лайнеры летают горизонтально при подъёмной силе в 50 г/см2, то есть используя только 5% от возможной подъёмной силы упругой среды в 1000 г/см2… Так что, подъёмная сила — это очень небольшая асимметрия большой силы, называемой атмосферным давлением. Причём вектор положительной разницы этой силы всегда перпендикулярен плоскости крыла.

Физики из NASA хотели вычислить подъёмную силу, но сели в лужу. Почему так получилось. А потому, что математика к природе вещей и движения не имеет никакого отношения, но они об этом словно не знали. Иначе говоря, в природе реально существует только то, что математик сосчитать не может. А что он может сосчитать — он придумал. И вообще, тот, кто пустил в физику математиков, сделал фатальную для неё, физики, ошибку. Сейчас мы вам кое-что объясним, не написав при этом ни одной формулы.

Трактат «О подъёмной силе»

Аксиома полётов: «Всё, что летает, делает это по причине асимметричного атмосферного давления на него».

Аксиома крыла: «Подъёмная сила любого крыла равна положительной разнице двух встречных атмосферных давлений на него – нижнего и верхнего».

Аксиома самолёта: «С хорошим движком даже дверь полетит – был бы положительный угол атаки».

Теорема 1. Идеальный аэродинамический профиль – это «беспрофиль», то есть плоское, как лезвие безопасной бритвы, крыло.

Теорема 2. Асимметричное атмосферное давление на плоское крыло возникает и при его нулевом угле наклона к вектору движения воздушного потока, если верхняя поверхность крыла испещрена микроскопическими неровностями, а нижняя – максимально гладкая.

Теорема 3. Подъёмная сила атакующего плоского крыла пропорциональна его площади, его углу атаки, его скорости и упругой плотности среды. А возникает она за счёт уплотнения упругого и инертного воздуха под быстрым крылом и пропорционального разрежения инертного воздуха в прилегающем слое над ним. Как диагональ делит прямоугольник на два равных треугольника, так и атакующий «беспрофиль» делит встречный атмосферный поток на две равнозначные и самостоятельные причины возникновения подъёмной силы.

Терема 4. Подъёмная сила беспрофильного крыла при машущем и вибрирующем движениях крыла насекомых и птиц возникает как на опускании, так и на подъёме крыла, так как при этом тоже образуются обтекающие крыло параллельные атмосферные потоки – верхний и нижний.

Терема 5. Пропеллирующее движение плоского крыла делает возможным возникновение подъёмной силы без поступательного движения насекомого, птицы или вертолёта, то есть при их зависании на месте. («Пропеллирующее» — значит, передней режущей кромкой крыла всегда вперёд, всегда опережая – что на взмахе, что на опускании крыла.)

Теорема 6. Идеальный аэродинамический профиль крыла сверхзвукового самолёта – это «перевёрнутый острый прямоугольный треугольник», когда верхняя поверхность тонкого крыла параллельна продольной оси фюзеляжа, а нижняя наклонена на крейсерский угол атаки примерно в 1 градус.

Теорема 7. Максимально лёгкое и максимально плоское крыло с изменяемой стреловидностью крыла и с изменяемым профилем крыла, имеющее «законцовки» крыла, а также различное качество аэродинамических покрытий верхней и нижней поверхностей — это идеальное крыло самолёта на все обозримые времена.

Примечания. Справедливости ради нужно отметить, что Природа всё вышесказанное знала задолго до нас. Плоские крылья птеродактилей и красивейшая дисперсия света на микроскопических неровностях верхних поверхностей плоских крыльев стрекоз, бабочек и птиц (особенно чёрных) и есть тому доказательство. Кстати, расправленное крыло любой птицы примерно наполовину его длины и примерно на 90% его площади – там, где нет костно-мышечной «арматуры», — это тоже максимально возможный беспрофиль. Причём нижняя поверхность крыла любой птицы всегда плотная и блестящая, а верхняя — всегда бархатистая; верхние поверхности самых современных Боингов словно матовые, а нижние гладкие с зеркальным блеском. Только различие в качестве аэродинамических покрытий противоположных несущих поверхностей якобы даёт Боингу до 7-ми процентов экономии топлива, так как позволяет летать самолёту горизонтально на меньших углах атаки, то есть с меньшим лобовым сопротивлением.

Шестой вывод уже довольно давно реализован в конструкции очень тонкого крыла «новой аэродинамики» сверхзвукового «МиГ-21» и лопасти несущего винта «перевёрнутой аэродинамики» самого тяжёлого вертолёта в мире — «Ми-26». Это техническое решение принесло нашей авиации несколько мировых рекордов.

Вывод: наша авиация развивалась не благодаря, а вопреки научной аэродинамике горбатых крыльев, то есть способом проб и ошибок или «методом тыка». Так что, слава интуиции наших конструкторов и их изобретательской жилке!

И ещё. Каждый, кто попытается вникнуть в научную аэродинамику, поглупеет буквально на глазах. И «Не осознать бедняге в заблужденье,/Как много лжи за ширмой исчисленья (Поздняков).

На рисунке вверху не хватает отрезка прямой линии или черты. Вот, собственно говоря, и всё.

Видео:Подъёмная сила крыла ● 4Скачать

Почему и как возникает подъемная сила

Почему могут летать птицы, несмотря на то что они тяжелее воздуха? Какие силы поднимают огромный пассажирский самолет, который может летать быстрее, выше и дальше любой птицы, ведь крылья его неподвижны? Почему планер, не имеющий мотора, может парить в воздухе? На все эти и многие другие вопросы дает ответ аэродинамика — наука, изучающая законы взаимодействия воздуха с движущимися в нем телами.

В развитии аэродинамики у нас в стране выдающуюся роль сыграл профессор Николай Егорович Жуковский (1847—1921) —«отец русской авиации», как назвал его В. И. Ленин.

Заслуга Жуковского состоит в том, что он первый объяснил образование подъемной силы крыла и сформулировал теорему для вычисления этой силы. Им была решена и другая проблема теории полета — объяснена сила тяги воздушного винта. Жуковский не только открыл законы, лежащие в основе теории полета, но и подготовил почву для бурного развития авиации в нашей стране. Он связал теоретическую аэродинамику с практикой авиации, дал возможность инженерам использовать достижения ученых-теоретиков.

В основанных Жуковским лабораториях и в созданных при них кружках выросла целая плеяда ученых, исследователей и конструкторов, обогативших своими трудами и открытиями не только русскую, но и мировую науку. Под научным руководством Жуковского был организован под Москвой Аэрогидродинамический институт. В этом институте удалось провести много весьма ценных исследований.

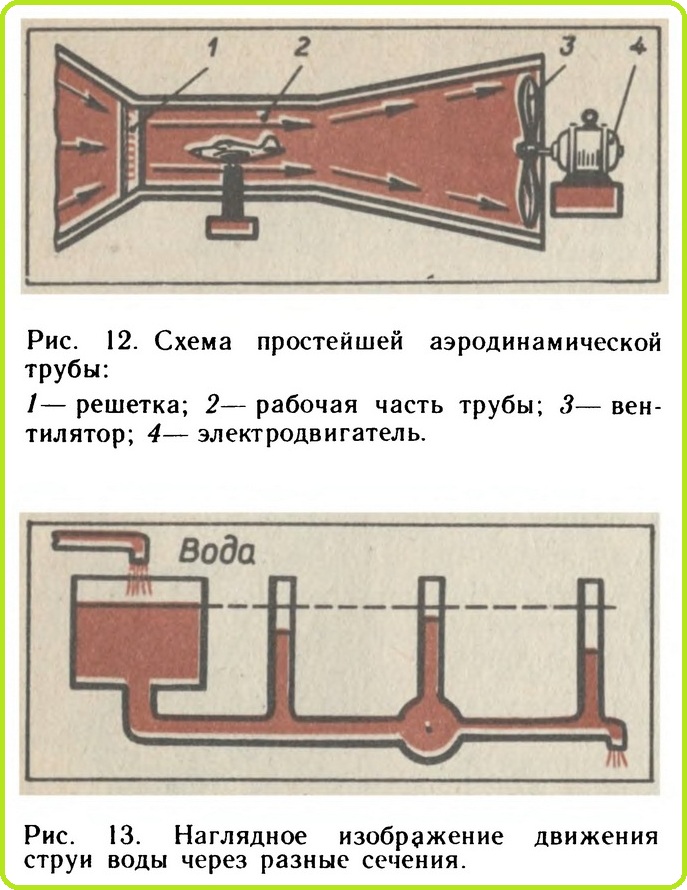
Основным приспособлением, служащим для изучения законов движения тел в воздухе, является аэродинамическая труба. Простейшая аэродинамическая труба представляет собой профилированный канал (рис. 12). В одном конце трубы установлен мощный вентилятор, приводимый во вращение электродвигателем. Когда вентилятор начинает работать, в канале трубы образуется воздушный поток. В зависимости от диаметров канала трубы и воздушного винта и мощности двигателя вентилятора можно получить различные скорости воздушного потока вплоть до сверхзвуковых. Современные аэродинамические трубы достигают гигантских размеров. В их каналах можно помещать для исследования не только модели, но и реальные самолеты.

Важнейшими законами аэродинамики являются закон сохранения массы (уравнение неразрывности) и закон сохранения энергии (уравнение Бернулли). Оба эти закона справедливы и для движущегося газа (воздуха), и для жидкости, поэтому проще будет ознакомиться с ними на примере движения воды. На рис. 13 изображена схема прибора, состоящего из открытого резервуара с водой, соединенного с трубкой, имеющий разные сечения. Согласно закону постоянства массы через каждое из этих сечений будет протекать в одну секунду одинаковый объем воды. Но если через неравные сечения в единицу времени протекает одинаковый объем воды, то, значит, через эти сечения вода движется с разными скоростями: чем меньше сечение, тем больше скорость воды (воздуха). В этом можно также убедиться, наблюдая за течением реки. Там, где русло узкое, течение воды быстрее.

Если к потокам жидкости в разных сечениях трубки подключить манометры, то они покажут, что при сужении струи, то есть при увеличении скорости воды (воздуха), давление в струе уменьшается, и наоборот. Это явление, описанное математиком Бернулли, позволяет установить связь между скоростью потока в данном сечении струи жидкости (газа) и давлением в этом же сечении.

Видео:Урок 135. Применения ур-ния Бернулли (ч.2). Подъемная сила крыла самолета (ч.1)Скачать

Возникновение подъемной силы

Описанное уравнением Бернулли явление позволяет объяснить возникновение аэродинамических сил, а главное подъемной силы крыла. В литературе это уравнение иногда называют законом Бернулли

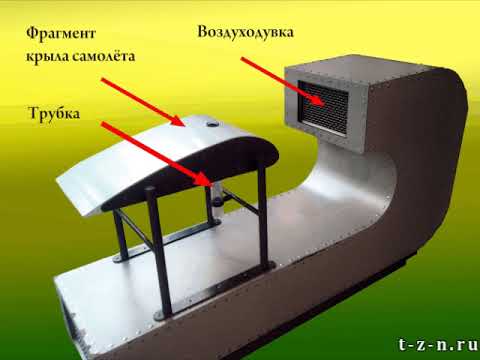
Рассмотрим природу возникновения подъемной силы. Опыты, проведенные в аэродинамических лабораториях, позволили установить, что при набегании на тело воздушного потока частицы воздуха обтекают тело. Картину обтекания тела воздухом легко наблюдать, если поместить тело в аэродинамической трубе, в подкрашенном потоке воздуха, кроме того, ее можно сфотографировать. Полученный снимок называют спектром обтекания.

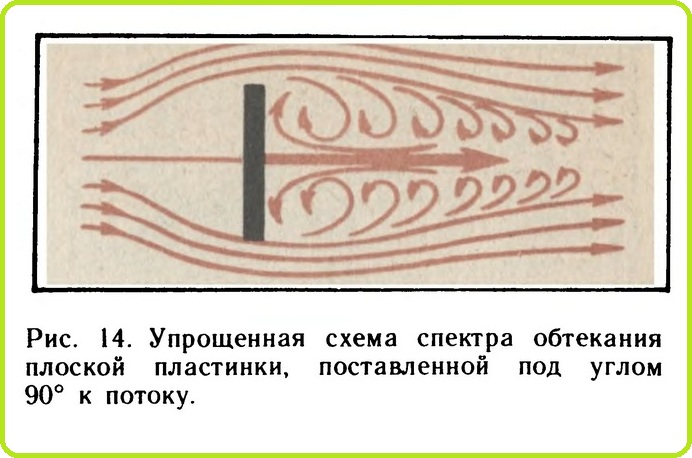
Упрощенная схема спектра обтекания плоской пластинки, поставленной под углом 90° к направлению потока, изображена на рис. 14.

Из рисунка видно, что в этом случае никакой подъемной силы не возникает. Воздух впереди пластинки создает подпор, плотность его струек повышается, а сзади пластинки воздух оказывается разреженным. Повышенной давление воздуха впереди пластинки и разрежение позади нее приводят к тому, что струйки воздуха с силой устремляются в разреженное пространство, закручиваются и образуют сзади пластинки те завихрения, которые мы и видим на спектре.

На рис. 15 дано схематическое изображение спектра обтекания пластинки, поставленной под острым углом к потоку. Под пластинкой давление повышается, а над ней вследствие срыва струй получается разрежение воздуха, т. е. давление понижается. Благодаря образующейся разности давлений и возникает аэродинамическая сила. Она направлена в сторону меньшего давления, т. е. назад и вверх. Отклонения аэродинамической силы от вертикали зависит от угла, под которым пластинка поставлена к потоку. Этот угол получил название угла атаки (его принято обозначать греческой буквой α — альфа).

Свойство плоской пластинки создавать подъемную силу, если на нее набегает под острым углом воздух (или вода), известно уже с давних времен. Примером тому служит воздушный змей и руль корабля, время изобретения которых теряется в веках.

Подъемная сила крыла (обозначим ее Y) возникает не только за счет угла атаки а, но также и благодаря, тому, что поперечное сечение крыла представляет собой чаще всего не симметричный профиль с более выпуклой верхней частью.

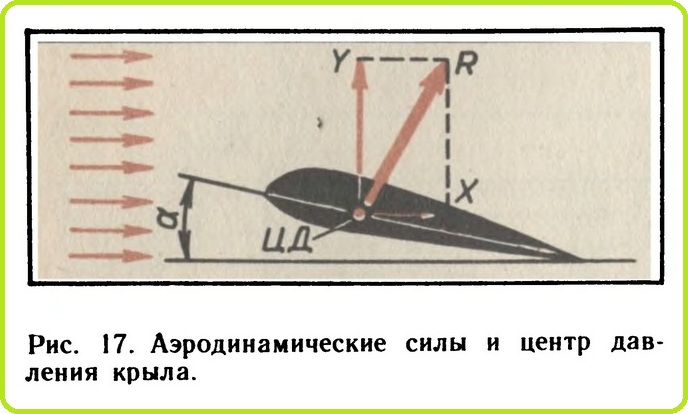
Крыло самолета или планера, перемещаясь, рассекает воздух. Одна часть струек встречного потока воздуха пойдет под крылом, другая— над ним (рис. 16). У крыла верхняя часть более выпуклая, чем нижняя, следовательно, верхним струйкам придется пройти больший путь, чем нижним. Однако количество воздуха, набегающего на крыло и стекающего с него, одинаково. значит, верхние струйки, чтобы не отстать от нижних, должны двигаться быстрее. В соответствии с уравнением Бернулли, если скорость воздушного потока под крылом меньше, чем над крылом, то давление под крылом, наоборот, будет больше, чем над ним. Эта разность давлений и создает аэродинамическую силу R (рис. 17), одной из составляющих которой является подъемная сила. Y. Подъемная сила крыла тем больше, чем больше угол атаки, кривизна профиля (его несущие свойства), площадь крыла, плотность воздуха и скорость полета υ, причем от скорости подъемная сила зависит в квадрате. Но следует помнить, что угол атаки должен быть меньше некоторого критического значения а_кр, при превышении которого подъемная сила падает.

Развивая подъемную силу, крыло всегда испытывает и лобовое сопротивления. Сила лобового сопротивления X направлена по потоку прямо против движения и, значит, тормозит его. Подъемная сила всегда перпендикулярна набегающему потоку. Из рисунка видно, что сила лобового сопротивления X и подъемная сила Y являются составляющими силы R по направлению скорости v и перпендикулярно ей. Сила R называется полной аэродинамической силой крыла. Точку приложения полной аэродинамической силы называют центром давления крыла (ЦД).

Подъемная сила летательного аппарата, уравновешивая его вес, дает возможность осуществлять полет, лобовое же сопротивление тормозит его движение. Отсюда ясно, что крылу надо придать такую форму, чтобы оно развивало как можно большее значение подъемной силы и в то же время давало малое лобовое сопротивление. Число, показывающее, во сколько раз подъемная сила больше лобового сопротивления, называется аэродинамическим качеством и обозначается буквой K.

А теперь подробнее рассмотрим природу возникновения сил сопротивления. Во время купания вы все, конечно, замечали, что в воде двигаться труднее. Это объясняется силой сопротивления воды. Как уже было сказано, воздух — газообразная среда, которая имеет определенную плотность и массу. И, перемещаясь в воздухе, мы также встречаем его сопротивление. Сила, которая мешает нам передвигаться в воздухе, называется силой сопротивления воздуха.

Движется ли тело с некоторой скоростью в неподвижном воздухе или, наоборот, тело неподвижно, а на него набегает поток воздуха с той же скоростью, сила сопротивления воздуха в обоих случаях будет одинаковой. Все дело в том, что воздух и тело движутся один относительно другого.

От каких же причин зависит сопротивление воздуха? Этих причин несколько. На рис. 18 изображена картина обтекания круглой пластинки. Если к этой пластинке спереди сделать конусообразную приставку, которая заполнила бы всю ту область перед пластинкой, где давление было повышено, то спереди давление значительно снизится. И хотя срыв струй и понижение давления позади составного тела будут такими же, как и за пластинкой, все же разность давлений и лобовое сопротивление значительно уменьшатся.

Чтобы избежать срыва струй, следует сделать еще и кормовую конусообразную приставку, заполнив ею всю область пониженного давления за пластиной.

Одновременное использование носовой и кормовой приставок определенной формы позволяет резко снизить лобовое сопротивление по сравнению с лобовым сопротивлением пластинки (примерно в 20—25 раз). Таким образом можно получить тело наиболее выгодной аэродинамической формы. В этом случае поток плавно разделяется передней частью тела, обтекает его и плавно стекает с кормовой части. Тела подобной формы называет удобообтекаемыми. Они и получили наибольшее распространение в авиации.

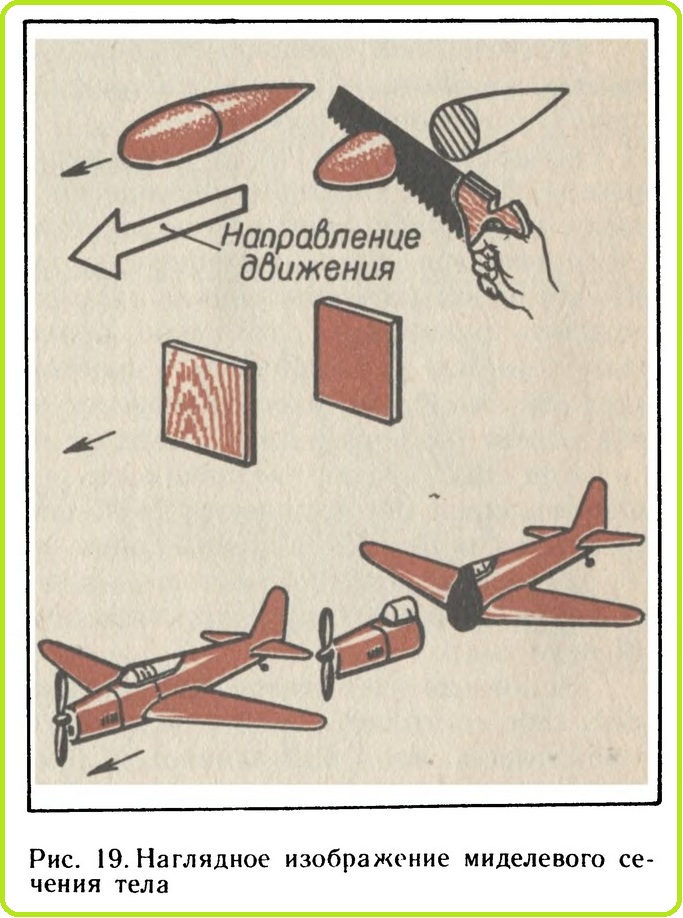
Что касается влияния размеров тела на сопротивление воздуха, то кажется ясным: чем больше тело, тем сильнее сопротивление. Однако здесь надо уточнить следующее: основной величиной, связанной с размерами тела и определяющей силу сопротивления при его движении, является наибольшая площадь сечения тела, перпендикулярного к направлению движения. какое сечение называется миделевым (рис. 19).

Но еще большее влияние на сопротивление оказывает скорость движения тела в воздухе. При движении тела с небольшой скоростью это сопротивление мало, а с ее увеличением быстро возрастает. При полете самолета на дозвуковых скоростях сопротивление растет прямо пропорционально квадрату скорости. Это значит, что если, например, скорость движения увеличить в два раза, то сопротивление возрастет в четыре раза, если скорость увеличить в три раза, то сопротивление возрастет в девять раз, и т. д. Аналогично, как об этом говорилось выше, скорость влияет и на значение подъемной силы.

Однако для скоростей, близких к скорости звука (340 м/с или 1224 км/ч), из-за влияния сжимаемости воздуха характер обтекания тел изменяется, сопротивление резко возрастает и этот закон уже не действует.

Таким образом, как и подъемная сила, сила лобового сопротивления зависит от угла атаки, формы профиля, плотности воздуха, площади сечения и квадрата скорости, хотя эти зависимости и имеют свои особенности.

Более методичная информация об подъемной силе можно прочитать в материале «Аэродинамические характеристики крыла», а так же, что такое САХ и как найти центр тяжести.