Уравнение бернулли и его экспериментальное подтверждение

Министерство высшего образования и науки РФ

«Казанский национальный исследовательский технологический университет»

Кафедра «Процессы и аппараты химической технологии» («ПАХТ»)

Лабораторная работа №4

«Экспериментальная демонстрация уравнения Бернулли»

студент группы 4191-44

доцент кафедры ПАХТ

Казань 2021
Название: Экспериментальная демонстрация уравнения Бернулли

1) уяснение физического смысла уравнения Бернулли;

2) определение потерь напора в трубопроводе переменного сечения;

3) ознакомление со способами измерения средней и локальной

скоростей движения жидкости.

Описание и схема установки:

Рис.1. Схема установки

1 – напорный бак, 2 – трубопровод переменного сечения, 3 – мерный

бак, 4 – сливной отсек мерного бака, 5, 7, 9 – вентиль, 6 – кран, 8 –

патрубок, 10 – пьезометрическая трубка, 11 – трубка Пито

­­ 1.Что называется напором?

В гидравлике энергия, отнесенная к единице веса жидкости, называется напором и измеряется высотой столба жидкости.

2.В чем заключается смысл уравнения Бернулли?

где w – скорость в рассматриваемом сечении элементарной струйки, м/с;

р – давление в том же сечении, Па ;

z – геометрическая высота 49 расположения этого сечения относительно произвольно выбранной горизонтальной плоскости сравнения О – О, м;

ρ – плотность жидкости, кг/м 3 ;

g – ускорение силы тяжести, м/с 2

В уравнении Бернулли =h_ск – скоростной напор; p/ρg = h_пз – пьезометрический напор; z – геометрический напор. Сумма геометрического и пьезометрического напоров называется статическим напором. Следовательно, уравнение Бернулли можно сформулировать следующим образом: сумма геометрического, пьезометрического и скоростного напоров (полный гидродинамический напор) в любом сечении потока невязкой жидкости есть величина постоянная. Из уравнения Бернулли следует, что увеличение какой-либо составляющей полного гидродинамического напора (например, скоростного напора) приводит к уменьшению другой составляющей (например, пьезометрического напора), и наоборот. Таким образом, уравнение Бернулли является математическим выражением закона сохранения и превращения механической энергии применительно к движущейся идеальной жидкости.

3.Как определяют полный и статический напоры?

Сумма геометрического и пьезометрического напоров называется статическим напором

Полный гидродинамический напор – это сумма геометрического, пьезометрического и скоростного напоров

4.Что представляет собой потерянный напор?

Потерянный напор∆h_i—j – это та удельная (отнесенная к единице веса) механическая энергия, которая перешла в теплоту при движении жидкости между сечениями i и j

трубы? В каком случае потерянный напор можно было бы

определить по показаниям пьезометрических трубок?

6.Как измеряется скоростной напор? Какой скорости соответствует полученный таким способом скоростной напор?

Трубка Пито и пьезометрическая трубка должны быть установлены так, чтобы центры сечений на входе в эти трубки лежали в исследуемом сечении трубопровода. По разности уровней в них определяют скоростной напор и соответственно местную скорость в точке потока, совпадающей с центром сечения входа в трубку Пито:

По величине скоростного напора для каждого сечения вычисляется местная скорость движения жидкости

7.Как определяются средняя и местная скорости течения жидкости?

Величина средней скорости в сечениях определяется из уравнения расхода:

Где расход ; , V- объем воды, равный емкости мерного бака, t- – время заполнения мерного бака

По величине скоростного напора для каждого сечения вычисляется местная скорость движения жидкости

8.Что представляет собой диаграмма Бернулли?

Диаграмма уравнения Бернулли является графическим представлением изменения различных слагаемых уравнения Бернулли по длине трубопровода. Диаграмма характеризует удельную механическую энергию потока и включает в себя три линии: линию полного напора, пьезометрическую линию и линию геометрического напора.

Линия полного напора характеризует полную удельную механическую энергию, то есть сумму кинетической и потенциальной энергий

Пьезометрическая линия характеризует удельную потенциальную энергию потока и представляет сумму двух слагаемых

Геометрическая линия, или линия геометрического напора характеризует уклон трубопровода, т. е. изменение координаты z оси трубопровода.

9.Как строится линия полного напора?

Линия полного напора идеальной жидкости проводится параллельно оси абсцисс на расстоянии (hпз1+z1) от плоскости сравнения. За счет потерь на трение линия полного напора вязкой жидкости на каждом прямом участке трубы должна иметь некоторый уклон в сторону течения жидкости. Однако на данной экспериментальной установке эти потери очень малы. Поэтому на каждом участке через точки полных напоров в данных сечениях проводятся условно с небольшим наклоном линии полного напора до границ сужений а, b, c. Затем точки пересечения линий полных напоров с границами сужений соединяют отрезками прямых. В сужениях между отдельными участками проис- 55 ходит деформация потока, что приводит к вихреобразованию и к более резкому падению полного напора, чем на прямых участках трубопровода.

10.Как строится линия статического напора?

Линия статического напора на прямых участках проводится параллельно соответствующим линиям полного напора, поскольку на прямых участках скорость потока (и скоростные напоры) не изменяется. Как это следует из уравнения Бернулли, в сужениях происходит сначала резкое уменьшение, а затем возрастание статического напора. Так как в местах сужений не осуществляются измерения напоров, линия статического напора в сечениях а, b, c проводится произвольно

11.Как по диаграмме Бернулли определить потерянный напор?

Вычесть из значения полного напора в начальном сечении значение полного напора в конечном сечении рассматриваемых участков

12.Приведите примеры и дайте объяснение использованию

уравнения Бернулли в технике

Уравнение Бернулли широко применяется в технике, как для выполнения гидравлических расчетов, так и для решения ряда практических задач. Одной из таких задач является измерение скорости и расхода жидкости.

Трубка полного напора (или трубка Пито) служит для измерения скорости, например, в трубе. Если установить в этом потоке трубку, изогнутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость υ частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.

На этом же принципе основано измерение скорости полета самолета.

Запишем уравнение Бернулли для струйки, которая набегает на трубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0-0 (невозмущенный поток) и 1-1 (где υ = 0), получаем

Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р2 ≈ р0, следовательно из предыдущего имеем

.

Карбюратор поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешения его с потоком воздуха . Поток воздуха; засасываемого в двигатель, сужается в том месте, где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха.

Найдем соотношение между массовыми расходами бензина Qб и воздуха Qв при заданных размерах D и d и коэффициентах сопротивления воздушного канала (до сечения 2-2) ζв и жиклера ζж (сопротивлением бензотрубки пренебрегаем).

З аписав уравнение Бернулли для потока воздуха (сечение 0-0 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z1 = z2 и α = 1):

Учитывая, что массовые расходы и , получим

Обработка экспериментальных данных

t = 124 сек V=28

№ сечения	Z, см	hпз, см	hпт, см	Ṽ ,	ʌh1₋j, м	hск, м	Wimax,	Ŵi,
1	8	55	56	225	0	0.01	4,43	0,39
2	1	46	52		0.11	0.06	10,85	0,65
3	0	27	48		0.16	0.21	20,3	1,46
4	0	14	16		0.48	0.02	6,3	0,59

D₁=27мм

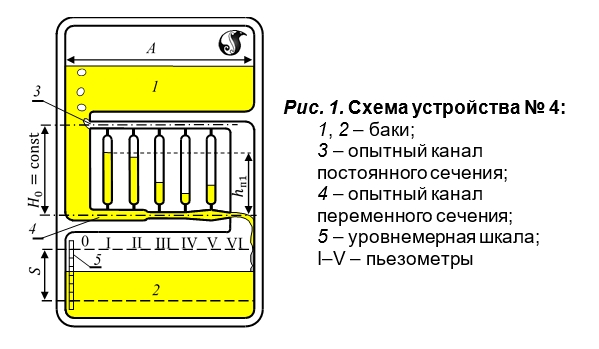
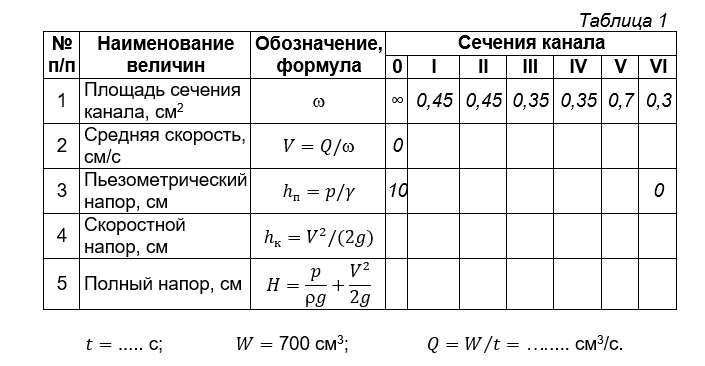
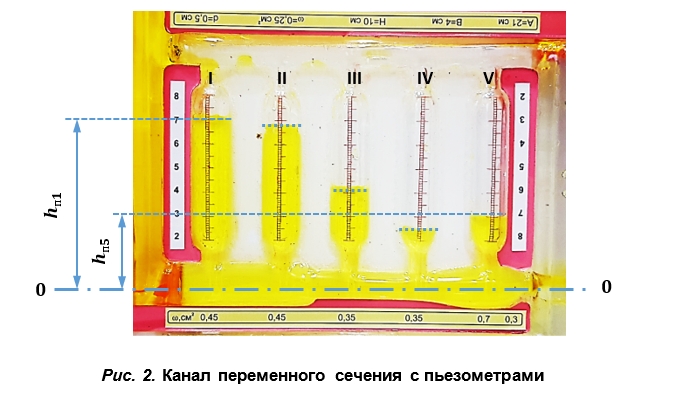
м

м

Видео:Закон БернуллиСкачать

Дистанционная лабораторная работа 5 по иллюстрации уравнения Бернулли

Цель работы. Опытное подтверждение уравнения Д. Бернулли, т. е. понижения механической энергии по течению и перехода потенциальной энергии в кинетическую и обратно (связи давления со скоростью).

Задание. На основе замеров при просмотре фильма и анализе фотографии течения жидкости в канале переменного сечения в устройстве № 4 построить линии энергий для потока и проверить их соответствие уравнению Бернулли.

Описание устройства № 4. Устройство № 4 содержит баки 1 и 2, сообщаемые через опытные каналы постоянного 3 и переменного 4 сечений (рис. 1). Каналы соединены между собой равномерно расположенными пьезометрами I–V, служащими для измерения пьезометрических напоров в характерных сечениях. Устройство заполнено подкрашенной водой.

В одном из баков предусмотрена шкала 5 для измерения уровня воды. При перевертывании устройства, благодаря постоянству напора истечения Н о во времени, обеспечивается установившееся движение воды в нижнем канале. Другой канал в это время пропускает воздух, вытесняемый жидкостью из нижнего бака в верхний.

Порядок выполнения работы.

1. Зарисовать схему устройства № 4 и составить таблицу следующего вида.

2. Посмотреть фильм с демонстрацией течения воды через канал переменного сечения в устройстве № 4 и секундомером замерить время t полного опорожнения верхнего бака.

3. Под таблицей записать значение времени t t опорожнения бака, объем бака принять равным W=700 см 3 и определить расход Q=W/t Q = W t .

4. В строке (стр.) 2 рассчитать среднюю скорость течения жидкости в каждом сечении канала: V=Q / w ω Скорость в нулевом сечении (перед входом в канал) принять равной нулю.

5. На фотографии канала с пьезометрами (рис. 2) снять показания пьезометров h_П1 . . . . h_П5 и записать их в стр. 3. В сечении VI пьезометрический напор равен 0.

6. В стр. 4 определить скоростной напор h_к в сечениях канала. Принять g = 981 см/с 2 .

7. В стр. 5 определить полный напор H H (полную удельную энергию) в каждом сечении. Так как опытный канал горизонтальный и плоскость сравнения 0–0 проведена через его ось, то геометрический напор z₁= z₂= 0 .

8. Вычертить в масштабе канал с осями пьезометров (рис. 3). Отложить от оси канала пьезометрические напоры h_П h _п на осях пьезометров, наметить уровни жидкости и соединить их между собой и центром выходного сечения VI , как показано на рис. 3. Получится пьезометрическая линия, показывающая изменение потенциальной энергии (давления) вдоль потока. Для получения напорной линии (линии полной механической энергии) нужно отложить от оси канала полные напоры Н и соединить полученные точки, как показано на рис. 3.

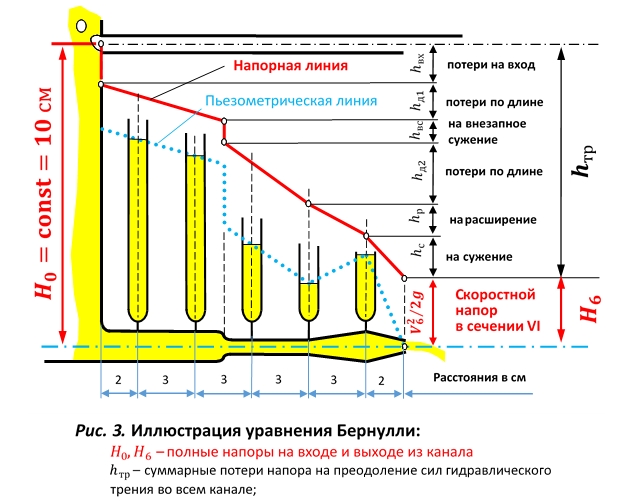
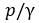9. Проанализировать изменения полной механической H , потенциальной и кинетической V 2 /(2g) V 2 /(2 g ) энергий жидкости вдоль потока и проверить их соответствие нижеприведенным правилам построения линий энергий, вытекающим из уравнения Бернулли.

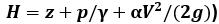А. Напорная линия (полный напор постоянно понижается по течению (если на рассматриваемом участке нет насоса) ввиду необратимого преобразования механической энергии в тепловую при преодолении потоком сил гидравлического трения. Причем уклон линии (потери напора h тр ) тем больше, чем меньше сечение участка потока (см. рис. 3).

Б. Пьезометрическая линия отражает изменение потенциальной энергии (z + ) , и, в отличие от напорной, может не только понижаться, но и повышаться по течению. Это происходит при расширении потока (см. рис. 2, 3) за счет повышения давления p ввиду уменьшения скорости V . Пьезометрическая линия проходит через центр тяжести выходного сечения канала (трубопровода) при истечении жидкости в атмосферу и ниже оси канала, если давление в нем меньше атмосферного.

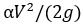В. Расстояние между пьезометрической и напорной линиями численно равно кинетической энергии α V 2 /( 2 g ) и поэтому обратно пропорционально диаметру трубы. Для участков потоков постоянного сечения средние скорости одинаковы по пути, поэтому такие линии, как правило, параллельны между собой (рис. 3). Эти линии для потоков в конфузорах (конических сходящихся патрубках) расходятся, а в диффузорах (конических расходящихся патрубках) – сходятся. В баках и водоёмах, где жидкость не движется (V=0) ( V =0) , напорная и пьезометрическая линии энергий совпадают со свободной поверхностью, если она находится под атмосферным давлением.

10. Записать выводы , где указать какие знания и навыки получены при выполнении данной работы и в каких сферах инженерной деятельности они могут быть применены.

📹 Видео

Экспериментальное исследование уравнения БернуллиСкачать

10. Уравнения БернуллиСкачать

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Уравнение Бернулли гидравликаСкачать

Уравнение БернуллиСкачать

Закон БернуллиСкачать

Работа 4. Экспериментальная демонстрация уравнения БернуллиСкачать

ЛР3 Уравнение БернуллиСкачать

Галилео. Эксперимент. Закон БернуллиСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Уравнение БернуллиСкачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать

Дистанционная работа 5 - иллюстрация уравнения БернуллиСкачать

Уравнение Бернулли Метод БернуллиСкачать

Уравнение Бернулли для потока жидкостиСкачать