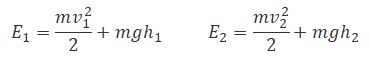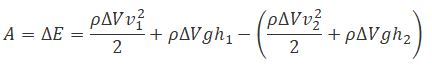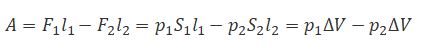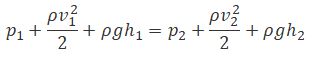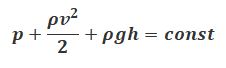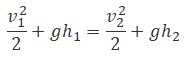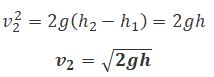Уравнение бернулли для стационарного течения идеальной несжимаемой жидкости формула торричелли (4 видео)

Уравнение Бернулли для жидкости (газа). Теорема Торричелли.

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

p— плотность жидкости,

v— скорость потока,

h— высота, на которой находится рассматриваемый элемент жидкости,

p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

g— ускорение свободного падения

Теорема Торричелли – связывает скорость истечения жидкости из малого отверстия в открытом сосуде с высотой жидкости над отверстием [1] .

Формула Торричелли утверждает, что скорость истечения жидкости через отверстие в тонкой стенке, находящееся в ёмкости на глубине от поверхности, такая же, как и у тела, свободно падающего с высоты [2] , то есть

где – ускорение свободного падения.

Сформулируйте закон всемирного тяготения. Получите формулу для первой космической скорости.

Закон всемирного тяготения: все тела притягиваются друг к другу с некоторой силой, которая для точечных и шарообразных тел определяется следущей формулой:

Уравнение бернулли для стационарного течения идеальной несжимаемой жидкости формула торричелли

где G = 6,67∙10 –11 м 3 /кг∙с 2 – гравитационная постоянная

Первая космическая скорость — это минимальная скорость, которую необходимо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, то есть превратиться в искусственный спутник Земли. На спутник, движущийся по круговой орбите радиусом r, действует сила тяготения Земли, сообщающая ему нормальное ускорение. Первой космической скорости недостаточно для того чтобы тело могло выйти из сферы земного притяжения.

Эскалатор метро движется вверх со скоростью 0,75 м/с. С какой скоростью и в каком направлении надо идти по эскалатору, чтобы быть все время на уровне одного из фонарей освещения туннеля?

Может ли человек, стоящий на идеально гладкой горизонтальной (ледяной) площадке, сдвинуться с места, не опираясь острым предметом о лед?

Может, отбрасывая от себя какие-то предметы

Билет 27.

Неинерциальные системы отсчета. Силы инерции.

Неинерциальная система отсчета – всякая система отсчета, движущаяся с ускорение относительно инерциальной, другими словами это та в которой не выполняется 1 закон Ньютона.

Сила инерции – векторная физическая величина численно равная произведению массы материальной точки на ее ускорение и направленная противоположно ускорению.

Почему возникает ускорение при равномерном движении материальной точки по окружности? Получите формулу для этого ускорения.

Направление скорости меняется значит присутствует ускорение. При равномерном движении по окружности возникает центростремительное ускорение, направленное в центр окружности.

Вывод формулы:

Связь между модулем линейной скорости υ и угловой скоростью ω:

υ = ωR.

3. Тело массой m равномерно поднимают на высоту h. В каком из указанных на рисунке случаев (1, 2, или 3) совершается большая работа? Чему равна величина совершаемой работы в каждом случае? Какая энергия изменялась в процессе подъема?

Содержание

Формула уравнения Бернулли
Определение и формула уравнения Бернулли
Частные случаи уравнения Бернулли
Следствие уравнения Бернулли
Примеры решения задач
Уравнение бернулли для стационарного течения идеальной несжимаемой жидкости формула торричелли
📸 Видео

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Формула уравнения Бернулли

Видео:Закон БернуллиСкачать

Определение и формула уравнения Бернулли

При рассмотрении движения жидкости очень часто считают, что перемещение одних частей жидкости относительно других не порождает сил трения. При этом жидкость, у которой вязкость (внутреннее трение) равна нулю, носит название идеальной.

Сжимаемой называют жидкость, плотность которой изменяется и может зависеть от температуры и давления.

Баротропной называют жидкость (или газ), плотность которой валяется функцией давления (не является функцией температуры).

Течение жидкости или газа называют стационарным, если скорость и давление жидкости остаются постоянными в каждой точке жидкости (газа).

Установившееся течение идеальной баротропной жидкости в потенциальном поле сил подчиняется уравнению Бернулли:

где $varphi_$ – потенциал поля массовых сил; C – величина постоянная для всех точек, которые принадлежат одной линии тока и переменная при переходе к другой линии тока; $rho$ – плотность идеальной жидкости; p – давление, v – скорость жидкости.

Видео:14. Движение идеальной жидкостиСкачать

Частные случаи уравнения Бернулли

При воздействии на жидкость только силы тяжести (нет других массовых сил), то потенциал поля можно представить:

где g – ускорение свободного падения, ось OZ имеет направление вверх (z – координата (или высота) по данной оси), тогда уравнение Бернулли можно записать как:

В том случае, если идеальную жидкость можно считать несжимаемой, уравнение Бернулли применяют в виде:

где $frac<rho v^>$ – называют скоростным напором или динамическим давлением; p – статическое давление в той точке пространства, где расположен центр массы исследуемого элемента жидкости; $frac<p^>$ – носит название пьезометрической высоты; $frac<v^>$ – скоростная высота, z – высота на которой находится элемент жидкости, который рассматривается.

Расчеты, которые проводят для реальных жидкостей с применением уравнения Бернулли, дают неплохие результаты.

Видео:Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Следствие уравнения Бернулли

1. Пусть все точки текущей жидкости имеют одинаковые величины скоростей. В таком случае для любых произвольных точек, относящихся к одной линии тока, выполняется равенство:

где p₁ и p₂ – давления в точках жидкости, находящихся на высоте z₁ и z₂, соответственно по вертикальной оси OZ.

Выражение (5) означает, что распределение давления является таким же, как в жидкости, находящейся в покое.

2. Для линии тока, если она горизонтальна уравнение Бернулли (3) примет вид:

что означает: давление оказывается меньше там, где скорость больше.

Видео:Уравнение Бернулли гидравликаСкачать

Примеры решения задач

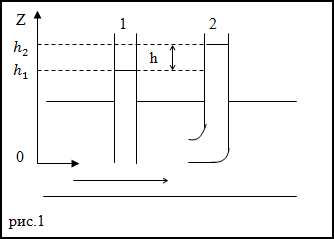
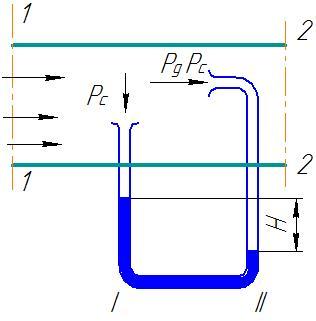
Задание. Какова скорость течения воды в горизонтальной трубе рис.1? Если в манометрических трубках, указанных на том же рис.1 разность уровней жидкости равна h. Считайте, что диаметры трубок одинаковы.

Решение. В качестве основы для решения задачи используем уравнение Бернулли в виде:

Запишем уравнение Бернулли для трубки тока в месте нахождения манометрических трубок (1) и (2) (используем (1.1)):

Для линии тока при постоянной скорости течения жидкости выполняется:

$$frac<rho v^>=rho gleft(h_-h_right)=rho g h rightarrow v=sqrt$$

Ответ. $v=sqrt$

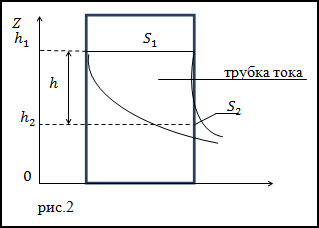
Задание. Используя уравнение Бернулли для идеальной несжимаемой жидкости, рассматривая истечение ее из маленького отверстия в широком открытом сосуде, получите формулу Торричелли: $v=sqrt$, где h=h₂-h₁ — высота открытой поверхности жидкости над отверстием, v – скорость истечения жидкости из отверстия.

Решение. Сделаем рисунок.

Рассмотрим рис.2. Выделим в жидкости трубку тока с сечениями S₁ – площадь открытой поверхности жидкости, S₂ – площадь сечения струи из отверстия. Будем считать, что для всех точек каждого из данных сечений скорость жидкости (v) и высота (h) над избранным начальным уровнем одинаковы. Значит к рассматриваемым сечениям применимо уравнение Бернулли:

где для двух рассматриваемых сечений давления p₁=p₂=p (p — атмосферное давление), скоростью перемещения открытой поверхности можно пренебречь, так как она мала. Уравнение (2.1) двух сечений трубки тока в таком случае упрощается до равенства:

$$rho g h_=frac<rho v^>+rho g h_ rightarrow frac<v^>=g h_-g h_ rightarrow v=sqrt(2.2)$$

здесь v – скорость, с которой вытекает жидкость из отверстия.

Видео:Уравнение Бернулли для потока жидкостиСкачать

Уравнение бернулли для стационарного течения идеальной несжимаемой жидкости формула торричелли

Гидродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа.

Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.

Идеальная среда

Гидродинамика изучает поведение идеальной жидкости — воображаемой среды без вязкости, сил трения и теплопроводности. Касательные напряжения равны нулю. Её можно представить, как систему небольших упругих шаров с пренебрежимо малым объёмом, не прилипающих друг к другу. Они часто сталкиваются друг с другом. Поэтому каждый шар переносит при движении массу, импульс, момент импульса, энергию.

Ламинарное и турбулентное движения жидкости

Экспериментально установлено, что в природе существуют два различных вида движения потока — ламинарное (слоистое, упорядоченное), при котором отдельные слои жидкости скользят друг относительно друга, и турбулентное (неупорядоченное), когда частицы жидкости движутся по сложным, все время изменяющимся траекториям.

Вследствие этого затрата энергии на турбулентное движение потока больше, чем на ламинарное.

Турбулентность — название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средний значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов. Происходит их нелинейное вихревое взаимодействие и распространение в пространстве и времени.

Турбулентность может возникать и при нарушении сплошности среды, например, при кавитации (кипении). При опрокидывании и разрушении волны прибоя возникает многофазная смесь воды, воздуха, пены. Мгновенные параметры среды становятся хаотичными.

Ламинарное течение

Отличие ламинарного течения от турбулентного состоит в характере и направлении водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости.

Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.

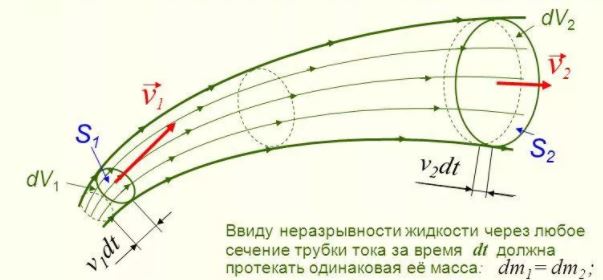
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока. Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

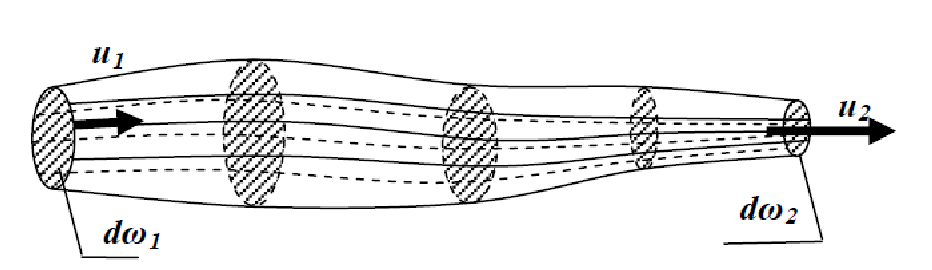
Трубка тока — трубчатая поверхность, ограниченная линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.

Для случая установившегося движения элементарной струйке придаются следующие свойства:

форма элементарной струйки остается неизменной с течением времени;
через стенки элементарной струйки движение жидкости не происходит (обмена энергией жидкости между элементарными струйками нет);
вследствие малости поперечного сечения элементарной струйки скорость и гидродинамическое давление во всех точках ее поперечного сечения одинаковы.

Уравнение неразрывности жидкости

В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то за время Δ t через сечение S проходит объем жидкости SvΔ t; следовательно, за 1 с через S 1 пройдет объем жидкости S 1 v 1 , где v 1 — скорость течения жидкости в месте сечения S 1 . Через сечение S 2 за 1 с пройдет объем жидкости S 2 v 2 , где v 2 — скорость течения жидкости в месте сечения S 2 . Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ = const), то через сечение S 2 пройдет такой же объем жидкости, как и через сечение S 1 , т. е.

Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.

Уравнение Бернулли

При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии.

Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.

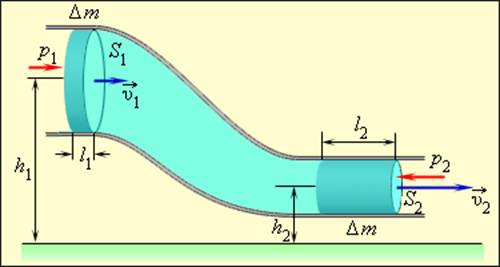
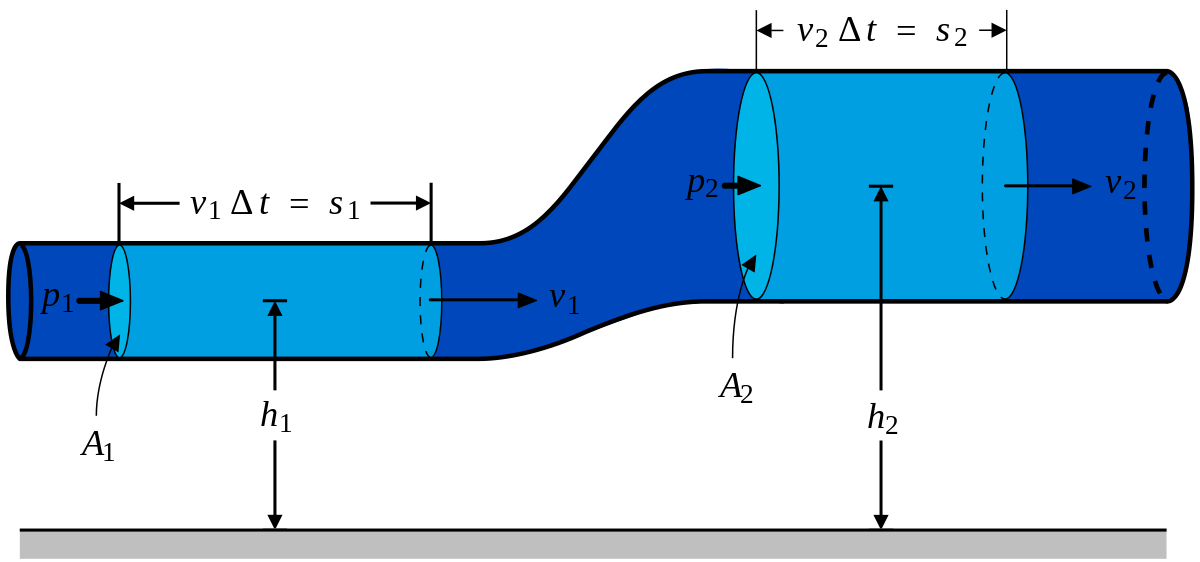
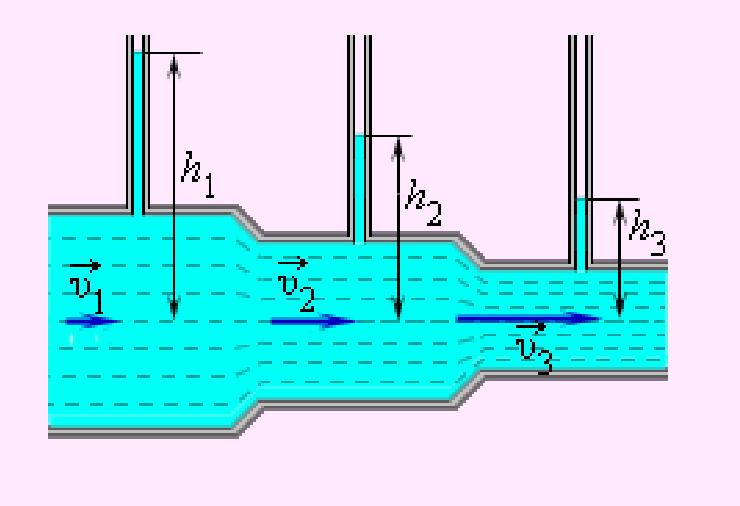
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах. У идеальной жидкости трение полностью отсутствует.

Выделим в стационарно текущей несжимаемой идеальной жидкости трубку тока, ограниченную сечениями S₁ и S₂, по которой жидкость течет слева направо. Пусть в месте сечения S₁ скорость течения v₁ давление р₁ и высота, на которой это сечение расположено, h₁. Аналогично, в месте сечения S₂ скорость течения v₂, давление р₂, высота сечения h₂. За малый промежуток времени Δt жидкость перемещается от сечения S₁ к сечениюS‘₁, от S₂ к S’₂.

Согласно закону сохранения энергии, изменение полной энергии Е₂ — Е₁ идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы т жидкости, где

— полные энергии жидкости массой т в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S₁ и S₂, за рассматриваемый малый промежуток времени Δt:

где р — статическое давление (давление жидкости на поверхность обтекаемого ею тела),

ρv 2 /2 — динамическое давление.

1. Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности следует, что при те чении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше.

Это можно продемонстрировать, установив вдоль трубы ряд манометров. В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

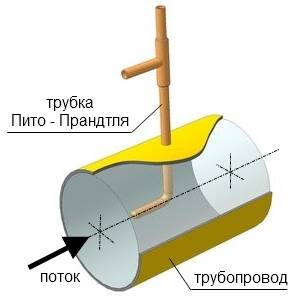
2. Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля. Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р₀), с помощью другой — статическое (р).Манометром измеряется разность давлений:

где ρ — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:

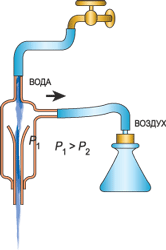
3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса. Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. = 133,32 Па).

4. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₂ выхода ее из отверстия). Напишем для них уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p₁ = p₂ , то уравнение будет иметь вид

Из уравнения неразрывности следует, что v₂/v₁ = S₁/S₂, где S₁ и S₂ — площади поперечных сечений сосуда и отверстия. Если S₁>>S₂, то членом v 2 ₁/2 можно пренебречь и