Уравнение бернулли для невязкой и вязкой жидкости (6 видео)

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Содержание

Смысл уравнения Бернулли
Уравнение Бернулли для элементарной струйки реальной жидкости
Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для потоков вязкой и невязкой жидкостей
Гидравлика
💥 Видео

Видео:Закон БернуллиСкачать

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— h_лп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— h_мп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнение Бернулли для потоков вязкой и невязкой жидкостей

Для элементарной струйки в потоке жидкости уравнение Бернулли имеет вид: , так как для потока: e_к = av 2 /2g, где a » 1.1 — опытный коэффициент кинетической энергии, то: — основное уравнение гидродинамики. Уравнение Бернулли устанавливает связь между скоростью движения, давлением и геометрическим расположением точек живого сечения потока.

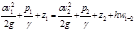
28 вопрос Энергетический и геометрический смысл уравнения Бернулли для потока жидкости

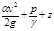
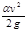
Энергетический смысл: — полная удельная энергия потока в живом сечении, так как — потенциальная удельная энергия давления, а z — потенциальная удельная энергия положения, то — удельная кинетическая энергия, где v — средняя скорость в сечении; hw_1-2 — затраты энергии на преодоление сил сопротивления.

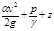
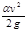
Геометрический смысл: — полный напор, так как — пьезометрический напор, а z — напор положения, то — скоростной напор; hw_1-2 — потерянный напор.

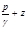
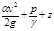
Пьезометрическая линия — ГМТ концов отрезков суммы . Пьезометрический уклон — изменение пьезометрической линии на единицу длинны. Напорная линия — ГМТ концов отрезков суммы . Гидравлический уклон — изменение напорной линии на единицу длинны

Равномерным движением называют такое движение, параметры которого не изменяются ни во времени, ни в пространстве. Таким образом, равномерное движение всегда является установившимся.

При неравномерном движении параметры изменяются в пространстве. Неравномерное движение может быть как неустановившимся, так и установившимся. Неустановившееся движение всегда является неравномерным.

При напорном движении поток соприкасается со всеми точками периметра живого сечения и не имеет свободной поверхности.

При безнапорном движении поток движется со свободной поверхностью.

. Совместное использование ур-ия Бернулли и гидравлического уравнения неразрывности

Уравнения могут быть использованы совместно при условии постоянного расхода

Q = ωύ = const. При установившемся движении несжимаемой жидкости произведение площади живого сечения на среднюю скорость потока является постоянной величиной.

ω1ύ1= ω2ύ2= ωύ = const, ύ1 ύ2= ω2ω1. Средние скорости потока обратно пропорциональны площадям соответствующих живых сечений.

Общая запись ур-ния Бернулли z1+p1ρg+α1 ύ212g= z2+p2ρg+α2 ύ222g+hw

гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (системгидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения [1] [2] . Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах учаска течения может быть и отрицательной (например, при эжекционном эффекте).

Гидравлические потери принято разделять на два вида:

потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;

местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.

Гидравлические потери выражают либо в потерях напора в линейных единицах столба среды, либо в единицах давления : , где — плотность среды, g —ускорение свободного падения.

режимы движения жидкости

Число Рейнольдса: Re=V*R/ν, где V – скорость, м/с; R — гидравлический радиус, м; v — кинематический коэффициент вязкости, м2/с. Re крит=2320.

Режим движения жидкости, при котором наблюдалось плавное, слоистое движение жидкости был назван ламинарным режимом движения жидкости (Re 2320).

Опыты показали, что переход от турбулентного режима к ламинарному происходит при определенной скорости (эта скорость называется критической), которая различна для разных жидкостей и диаметров труб; при этом критическая скорость растет с увеличением вязкости жидкости и с уменьшением диаметра труб.

Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока – число Рейнольдса Re=V*R/ν, где V – скорость, м/с; R — гидравлический радиус, м; v — кинематический коэффициент вязкости, м2/с.

потери напора по длине при турбулентном движении

Потери напора на трение по длине потока, возникающие при равномерном напорном движении жидкости в трубах, определяют по уравнению hдл=(λ*L*V^2)/(d*2g), где l – длина участка трубы, м; d – внутренний диаметр трубопровода, м; v – средняя скорость потока, м/с; g – ускорение свободного падения, м/с2; λ– безразмерный коэффициент гидравлического трения. Эта формула носит название формулы Дарси-Вейсбаха и является одной из основных формул гидродинамики.

Было установлено, что при больших числах Рейнольдса и высокой шероховатости коэффициент гидравлического трения λ в трубах совсем не зависит от вязкости жидкости (числа Рейнольдса), а зависит только от относительной шероховатости (в этих условиях трубы и русла называют вполне шероховатыми). Трубы же, в которых коэффициент λ зависит только от числа Рейнольдса и не зависит от относительной шероховатости, что бывает при сравнительно малых Re и k/d, называют гидравлически гладкими. При этом один и тот же трубопровод в одних условиях может быть гидравлически гладким, а в других – вполне шероховатым. Условия, в которых λ зависит и от числа Рейнольдса и от относительной шероховатости, называются переходной областью. Это объясняется тем, что при малых числах Рейнольдса вблизи стенок сохраняется сравнительно толстый ламинарный слой, и выступы шероховатости обтекаются жидкостью без образования и отрыва вихрей. Свойства поверхности стенок трубопровода в этом случае не влияют на сопротивление.

Коэффициент потерь напора по длине будет равен: ξ=λ*l/d

Коэффициент трения Дарси: λ=8*(U/V)^2

местные гидравлические сопротивления

Местные потери напора вызываются сопротивлениями в арматуре, фасонных частях и оборудовании, вследствие сужения и расширения потока, изменения направления движения жидкости, слияния и разделения потока и т. п.

Местные потери напора определяют как произведение скоростного напора непосредственно вблизи местного сопротивления ξ, по формуле hм=(ξ*V^2)/(2*g)

Коэффициенты местных сопротивлений, как правило, находят опытным путем.

Внезапное расширение потока. Этот случай поддается теоретическому обоснованию. Из опытов установлено, что поток жидкости, вытекающий из узкой трубы, не сразу заполняет все сечение широкой трубы; он отрывается от стенок и дальше двигается в виде расширяющейся струи. В кольцевом пространстве между струей и стенками трубы жидкость образует завихрения. На некотором расстоянии l от расширения трубопровода струя вновь заполняет все сечение. В результате вихревых движений жидкости между сечениями 1-1 и 2-2 идет постоянный обмен между струей и жидкостью в кольцевом пространстве. В результате этих явлений происходит переход механической энергии в тепловую, что и является причиной потерь напора. Диффузор.

формула Борда h вн.р.=(V1-V2)^2/2g

При внезапном сужении канала поток жидкости отрывается от стенок входного участка и лишь затем (в сечении 2 — 2) касается стенок канала меньшего размера. В этой области потока образуются две зоны интенсивного вихреобразования (как в широком участке трубы, так и в узком), в результате чего, как и в предыдущем случае, потери напора складываются из двух составляющих (потерь на трение и при сужении). Коэффициент потерь напора при гидравлическом сопротивлении внезапного сужения потока можно определить по эмпирической зависимости, предложенной Идельчиком: ξ=0,5*(1-ω2/ω1). Конфузор.

1) по параметрам, определяющим изменение площади живого сечения по длине потока:

(на непризматические и призматические (и цилиндрические).У непризматических русел форма и (или) геометрические размеры поперечного профиля меняются по длине русла. Поэтому площадь живого сечения потока является функцией длины русла и функцией глубины потока вдоль русла. В таком русле движение неравномерное. В призматических руслах форма и размеры элементов поперечного профиля по длине сохраняются неизменными. Площадь живого сечения потока может изменяться только в связи с изменением глубины потока.

2)По форме профиля поперечного сечения: правильной и неправильной формы. Призматические русла имеют правильную форму. Они могут быть прямоугольные, треугольные, трапецеидальные. Если поперечный профиль русла правильной формы очерчен кривой линией, окружностью или параболой определяемой по всей длине русла одним уравнением, то такое русло называется цилиндрическим . Правильную форму чаще всего имеют искусственные русла. К руслам неправильной формы относятся полигональные (составные) русла (рис. и русла естественных потоков

3)Открытые русла в зависимости от продольного уклона дна делятся на русла с положительным (прямым)геометрическим уклоном i >0, когда дно русла понижается в направлении движения потока; горизонтальные русла при i = 0 и русла с отрицательным (обратным) уклоном дна i Q и Q₀

Видео:Уравнение Бернулли гидравликаСкачать

Гидравлика

30. Уравнение Бернулли.

Уравнение Д. Бернулли для элементарной струйки невязкой и вязкой жидкости. Уравнение Бернулли, основное уравнение гидродинамики, связывающее (для установившегося течения) скорость текущей жидкости v, давление в ней р и высоту h расположения малого объёма жидкости над плоскостью отсчёта. Уравнение выведено Д. Бернулли в 1738г для струйки идеальной несжимаемой жидкости постоянной плотности , находящейся под действием только сил тяжести. интеграл Бернулли:

где Н – гидродинамический напор, м.

Уравнение можно записать для двух сечений элементарной струйки в виде равенства гидродинамических напоров в этих сечениях Н₁=Н₂

Выражение называется уравнением Бернулли для элементарной струйки невязкой жидкости.

Для реальной (вязкой) жидкости напор в любом вышележащем сечении всегда будет больше напора в нижележащем по течению сечении, т.к. часть энергии затрачивается на преодоление сил сопротивления, т.е. можно записать уравнение Бернулли для элементарной струйки вязкой жидкости в следующем виде:

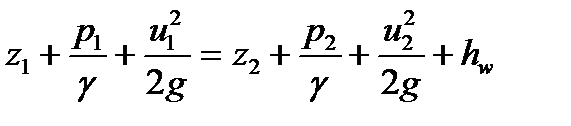
где h_w=Н₁ –Н₂ – удельные потери напора на преодоление всех сопротивлений (преодоление сил вязкости и сил трения между жидкостью и стенкой).

Уравнение Д. Бернулли для потока вязкой жидкости. При переходе от элементарной струйки к потоку вязкой жидкости, имеющему конечные размеры, необходимо учесть неравномерность распределения скоростей в живых сечениях и иметь представление о случаях возможного и невозможного применения уравнения Бернулли.

При движении вязкой жидкости вдоль твердой стенки ее скорость достигает максимального значения в центральной части потока и уменьшается до нуля возле стенки. Неравномерное распределение скоростей означает что движение вязкой жидкости сопровождается вращением частиц, вихреобразованием и перемешиванием. Поэтому, приходится вводить среднюю по сечению скорость v. Для приведения результатов расчетов по средней скорости вводится коэффициент Кориолиса , характеризующий неравномерное распределение скоростей в живом сечении потока, представляющий собой отношение кинетической энергии, подсчитанной по истинным скоростям сечения, к той же энергии, вычисленной по средней скорости в этом же сечении потока

Обычно в трубопроводах и каналах =1,05. 1,1, иногда приближенно принимают = 1.

Поэтому для потока вязкой жидкости с учетом неравномерности распределения скоростей по живому сечению уравнение Бернулли запишется следующим образом:

т.е. уравнение Бернулли устанавливает связь между высотными положениями частиц жидкости, давлением и скоростями в разных сечениях потока жидкости. Причем каждая из входящих в уравнение величин может изменяться, но сумма остается постоянной.

31. Режимы движения жидкостей

Существует два режима движения жидкости: ламинарный и турбулентный.

Ламинарное движение (от лат. lamina – пластинка), упорядоченное течение жидкости или газа, при котором жидкость (газ) перемещается как бы слоями, параллельными направлению течения. Наблюдаются или у очень вязких жидкостей: нефти, мазута, смазочных масел и в порах грунта при движении подземных вод, или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров. С увеличением скорости движения жидкости ламинарное движение может в некоторый момент перейти в неупорядоченное турбулентное, при этом резко изменяется сила сопротивления движению.

Турбулентное движение (от лат. turbulentus – бурный, беспорядочный), форма течения жидкости или газа, при которой их элементы совершают неупорядоченные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущихся жидкости или газа. Турбулентный режим движения жидкостей встречается при движении маловязких жидкостей (вода, бензин, спирт) в трубах, каналах, реках.

Характер режима движения жидкости зависит от соотношения действующих в них сил. Если при движении жидкости преобладают силы вязкости, то режим ламинарный, если преобладают силы инерции, то наблюдается турбулентный режим движения потока.

ЧИСЛО РЕЙНОЛЬДСА, нефиксированная величина, характеризующая режимы ПОТОКА ЖИДКОСТИ.

Рейнольдса Re = rvl/n, где r-плотность, l- линейные размеры, v- скорость потока, n- коэффициентом вязкости.

Низкие значения числа Рейнольдса указывают на ламинарное движение потока жидкости; при более высоких значениях поток становится турбулентным. Переход от ламинарного к турбулентному движению происходит при значении числа Рейнольдса, которое называют критическим(1200-20000).

32. Гидростатическое давление.

Жидкость, находящаяся в сосуде в состоянии покоя, давит на дно и стенки сосуда и на любое тело, погруженное в эту жидкость. Давление, оказываемое покоящейся жидкостью на любую соприкасающуюся с ней поверхность, называют гидростатическим.

Гидростатическое давление — давление, вызываемое весом жидкости. Гидростатическое давление:

— измеряется высотой столба воды в единицах длины или в атмосферах;

— зависит от координат точки, в которой оно измеряется.

Можно выделить 3 свойства гидростатического давления:

Первое свойство. Гидростатическое давление направлено всегда по внутренней нормали к поверхности, на которую оно действует.

Второе свойство. Гидростатическое давление в любой точке жидкости действует одинаково по всем направлениям.

Третье свойство. Гидростатическое давление в точке зависит только от ее координат в пространстве, т.е. р=f(х,у,z). ( т.е по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться.)

Давление, производимое покоящейся жидкостью, называется гидростатическим давлением.

рассчитать это давление?

Выделяем столб жидкости высотой h и площадью основания S;

сила давления воды на основание:

F = P – весу жидкости,

F = P = mg, m = p • V,

Приравниваем формулы (1) и (2):

33. Физические свойства жидкости.

Жидкость — физическое тело, которое обладает свойством текучести, т. е. не имеющее способности самостоятельно сохранять свою форму. Текучесть жидкости обусловлена подвижностью молекул, составляющих жидкость.

Жидкостью называется агрегатное состояние вещества, промежуточное между твердым и газообразным. Жидкость характеризуется следующими свойствами: 1) сохраняет объем; 2) образует поверхность; 3) обладает прочностью на разрыв; 4) принимает форму сосуда; 5) обладает текучестью. Свойства жидкости с 1) по 3) подобны свойствам твёрдых тел, а свойство 4) — свойству газа.

Текучесть: Под действием внешних сил жидкость не сохраняет форму. В отличие от пластичных твёрдых тел, жидкость не имеет предела текучести: достаточно приложить малую внешнюю силу, чтобы жидкость потекла.

Плотность: Отношение массы тела m к его объему W (Наибольшая плотность пресных вод будет при температуре 4°С: = 1000 кг/м 3 )

Сохранение объёма: Жидкость чрезвычайно трудно сжать механически, поскольку, в отличие от газа, между молекулами очень мало свободного пространства. Давление, производимое на жидкость, заключенную в сосуд, передаётся без изменения в каждую точку объёма этой жидкости (закон Паскаля, справедлив также и для газов). Эта особенность, наряду с очень малой сжимаемостью, используется в гидравлических машинах.

Жидкости обычно расширяются при нагревании и уменьшают объём (сжимаются) при охлаждении. Впрочем, встречаются и исключения, например, вода сжимается при нагревании, при нормальном давлении и температуре от 0°С до приблизительно 4°С.

Вязкость: Определяется как способность оказывать сопротивление перемещению одной части жидкости относительно другой — то есть как внутреннее трение.

Образование свободной поверхности и поверхностное натяжение: Из-за сохранения объёма жидкость способна образовывать свободную поверхность. Такая поверхность является поверхностью раздела фаз данного вещества: по одну сторону находится жидкая фаза, по другую — газообразная (пар), и, возможно, другие газы, например, воздух.

Если жидкая и газообразная фазы одного и того же вещества соприкасаются, возникают силы, которые стремятся уменьшить площадь поверхности раздела — силы поверхностного натяжения. Поверхность раздела ведёт себя как упругая мембрана, которая стремится стянуться.

Поверхностное натяжение может быть объяснено притяжением между молекулами жидкости.

Испарение и конденсация: Испарение – постепенный переход вещества из жидкости в газообразную фазу (пар).

Конденсация – обратный процесс, переход вещества из газообразного состояния в жидкое. При этом в жидкость переходит из пара больше молекул, чем в пар из жидкости.

Кипение: Процесс парообразования внутри жидкости. При достаточно высокой температуре давление пара становится выше давления внутри жидкости, и там начинают образовываться пузырьки пара, которые (в условиях земного притяжения) всплывают наверх.

Смачивание: поверхностное явление, возникающее при контакте жидкости с твёрдой поверхностью в присутствии пара, то есть на границах раздела трёх фаз.

Смешиваемость: способность жидкостей растворяться друг в друге. Пример смешиваемых жидкостей: вода и этиловый спирт, пример несмешиваемых: вода и жидкое масло.

Диффузия: При нахождении в сосуде двух смешиваемых жидкостей молекулы в результате теплового движения начинают постепенно проходить через поверхность раздела, и таким образом жидкости постепенно смешиваются.

Прозрачность :Степень прозрачности часто используется для измерения определенных видов примесей и эффективности очистки воды. Прозрачность выражается толщиной слоя воды (см). Зависит не только от количества содержащихся в ней взвешенных веществ, но также от крупности, формы и цвета частиц взвеси.

Характер запаха определяется органолептически. Интенсивность его оценивается по пятибалльной шкале. Для оценки интенсивности запаха указывается разбавление воды, при котором он исчезает.

Водослив — преграда (порог), через которую переливается поток воды; в гидротехнике водосливом называется водосброс со свободным переливом воды через его гребень. Закономерности движения жидкости через водосливы имеют большое практическое значение. Гидравлический расчет плотин шлюзов, мостов, водопропускных труб ведется на основании теории водосливов. Водосливы широко применяются в гидротехническом и дорожном строительстве (водосливные плотины, водосбросы); также используются и качестве измерителей расхода жидкости – главным образом в гидравлических лабораториях, а также при гидрогеологических и гидрометрических изысканиях в полевой обстановке.

Часть потока, расположенная выше водослива, называется верхним бьефом, а ниже сооружения – нижним бьефом. Верхняя грань водослива, через которую происходит перелив жидкости из верхнего в нижний бьеф, называется порогом, или гребнем водослива.

Водосливы классифицируются по ряду признаков:

1) по форме поперечного сечения сливного порога, ( водослив с тонкой стенкой,водослив с широким порогом, и водослив практического профиля)

Водослив с тонкой стенкой: поток переливающийся через водослив с тонкой стенкой, имеет на всем своем протяжении неравномерный характер.

Водослив с широким порогом; на таком пороге устанавливается почти параллельно-струйное течение жидкости,

Водослив практического профиля, имеющий криволинейные очертания, соответствующие нижней поверхности струи жидкости в случае перелива через острый порог.

2) по плановому расположению, (прямым, боковым, косым, криволинейным или с боковым сжатием )

3) по условиям подхода жидкости к водосливу, (без бокового сжатия и водосливы с боковым сжатием. У первых перелив воды через порог происходит по всей ширине русла, а у вторых порог занимает только часть ширины подходного потока, который при переливе через водослив претерпевает сжатие с боков. Боковое сжатие отсутствует в том случае, если длина гребня водослива совпадает с шириной потока).

4) по форме водосливного отверстия, (быть прямоугольным, треугольным, трапецеидальным, параболическим).

5) по характеру сопряжения уровней воды верхнего и нижнего бьефов (разделяются на незатопленные, когда уровень потока в нижнем бьефе за водосливом не превышает гребня порога водослива, и затопленные, когда этот уровень выше, чем гребень порога (положение уровня в нижнем бьефе в последнем случае существенным образом влияет на величину расхода, пропускаемого через водослив).

Струя жидкости при переливе через водослив с тонкой стенкой претерпевает вертикальное сжатие. Площадь живого сечения потока над порогом водослива

где e_в – коэффициент вертикального сжатия потока.

Средняя скорость потока в сечении над порогом : v=j ,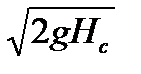

где H_с –возвышение уровня воды верхнего бьефа над центром тяжести водосливного отверстия.

Для прямоугольного отверстия v=j ,так как H_с=Н/2.Расход через водослив можно рассчитать по формуле

Q=w_cv=e_вbНj =e_вj* *b *H 3/2 .

Введем обозначение e_вj* =m_o и получим формулу для расхода через незатопленный прямоугольный водослив с тонкой стенкой без бокового сжатия Q= m_o b *H 3/2

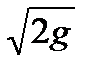
Величина m₀ – коэффициент расхода водослива с тонкой стенкой.

Расход жидкости в трапецеидальном водосливе находится по формуле

Q= m_o (b+0,8tga*H)H 3/2 ,

где a– угол наклона водослива по низу, b – ширина водослива по низу, m – коэффициент расхода, определяемый опытным путём.

При значении tga (уклон боковой стенки)=0,25 трапецеидальный водослив обладает свойством постоянства коэффициента расхода (m=0,42)при изменении напора H и применяется для измерения расхода. В этом случае Q=1,86bH 3/2 .

Для водослива треугольной формы

Q= m_o H 5/2 tga .

Наибольшее применение – имеет треугольный водослив с вырезом в форме прямоугольного треугольника? обычно используемый для измерения сравнительно небольших расходов жидкости. Для такого водослива

Q=1,343H 2,5 или Q=1,4H 2 .