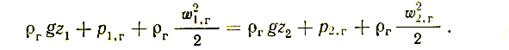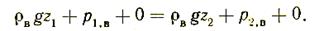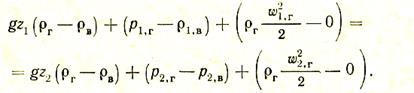Уравнение бернулли для несжимаемого газа и его сущность (2 видео)

Уравнение бернулли для несжимаемого газа и его сущность

С учетом выражений для кинетической энергии и энергии силы давления потока запишем уравнение Бернулли в виде

В соответствии с уравнением неразрывности массовый расход

Для идеального несжимаемого газа
= сonst.

Поэтому для идеального несжимаемого газа уравнение Бернулли запишем в виде

где
– скоростной напор ( динамическое давление, Па);
p – статическое давление, (Па).

Для идеального несжимаемого газа сумма скоростного напора и статического давления в струйке есть величина постоянная, т.е. с увеличением скорости V давление в струйке p падает, и наоборот.

Знание основных законов аэродинамики позволяет построить математическую модель картины обтекания тела свободным потоком (без учета пограничного слоя) и определить значения аэродинамических сил, зависящих от распределения давления по поверхности тела.

Видео:Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Уравнение Бернулли для несжимаемого газа

Это уравнение было опубликовано Даниилом Бернулли в 1738г. Оно представляет собой приложение закона о сохранении энергии к элементарной струйке. Рассмотрим полную энергию секундного массового расхода газа (1.5)

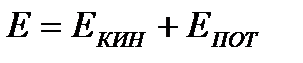
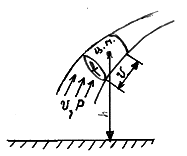
Рис. 1.5. К выводу уравнения Бернулли для несжимаемого газа

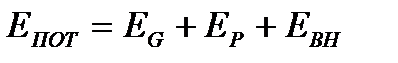
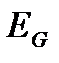
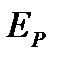
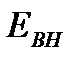
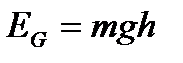
где — энергия положения, зависящая от высоты h;

— энергия давления;

— внутренняя энергия газа.

Для задач аэродинамики 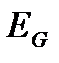=const, т. к. струйки, обтекающие самолёт в полете, находятся на одном энергетическом уровне (h=const).

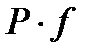
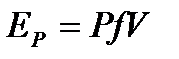
Энергия давления равна произведению работы силы давления , выполненной за 1 сек массой газа m (см. рис.1.5)

Внутренняя энергия меняется при изменении температуры газа: у несжимаемого газа во всех сечениях струйки плотность 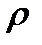=const , следовательно, и температура Т=const , т.е.

Кинетическая энергия секундного массового расход m определится по формуле:

Е_кин = ;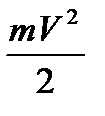

Просуммируем все виды энергии:

const + PfV + const + 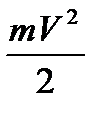= const,

PfV + 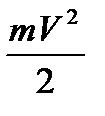= const.

Для несжимаемого газа согласно уравнению неразрывности струйки fV=const. Разделим все части уравнения на эту константу:

;

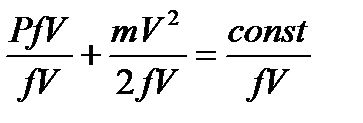
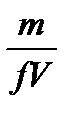
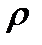
т.к. = , (масса газа, деленная на его объем),

то уравнение принимает вид:

P+ 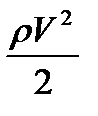= const.

где Р — статическое давление;

— скоростной напор (динамическое давление).

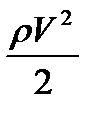
Читается уравнение так:

сумма статического и динамического давления вдоль струйки — величина постоянная.

Уравнение устанавливает обратную зависимость между скоростью потока и давлением в нём.

Следствие: чем больше скорость потока, тем меньше давление в нём.

Физический смысл членов уравнения.

Р — потенциальная энергия давления единицы объёма газа.

— кинетическая энергия единицы объёма газа.

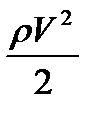
Дата добавления: 2016-12-27 ; просмотров: 5286 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Элементы теории движения реальных газов

При движении газа на каждый его объем будут действовать не только те силы, которые характерны для статики, но и другие, сильно усложняющие как явление в целом, так и его математическое описание. Для движения идеального газа этими дополнительными силами будут силы инерции, а для реального газа — силы инерции и трения (вязкости). В механике сплошных сред большое внимание уделяется выводу и использованию соответствующих математических уравнений, описывающих движение идеальных (уравнения Эйлера) и реальных сред (уравнения Навье — Стокса). Уравнения Навье — Стокса настолько сложны, что к настоящему времени решены лишь для крайне ограниченного числа случаев. Эта сложность вызвана сильным влиянием вязкости среды на различные аспекты процесса движения. В силу этого в допустимых случаях прибегают к решению уравнений Эйлера для движения идеальных сред с введением необходимых поправок и уточнений. Таким образом, получено одно из важнейших уравнений гидро- и аэродинамики — уравнение (закон) Бернулли.

Уравнение Бернулли. В практических условиях крайне распространенным является движение в трубах и каналах, когда газ через боковые стенки не расходуется. В таких случаях для расчетов применяется уравнение Бернулли, полученное для струйки тока (трубка тока), характерной тем, что расход газа в любом ее сечении остается неизменным (обмен газом между всем потоком и струйкой тока через ее боковые границы отсутствует).

Для несжимаемого газа (r = const) уравнение Бернулли при условии, что все его члены отнесены к единице объема, имеет вид

rgz +р +rw 2 /2 = const. (14)

В соответствии сэтим величина р является статическим давлением, величина rgz — геометрическим давлением, величина rw 2 /2 — динамическим давлением.

Уравнение Бернулли представляет собой закон сохранения энергии, поскольку сумма р + rgz характеризует потенциальную, а величина rw 2 /2 — кинетическую энергию.

Как отмечалось выше, в металлургической теплотехнике в подавляющем большинстве случаев пользуются давлением, избыточным над атмосферным. Поэтому полезно уравнение Бернулли привести к такому виду, при котором все члены его были бы выражены в избыточных давлениях. Для этого представим себе канал, окруженный воздухом плотностью r_в, по которому движется газ плотностью r_г. Принимая плотности газа и воздуха неизменными, напишем уравнение Бернулли и для газа и воздуха применительно к сечениям канала z₁и z₂.

Уравнение для газа

Уравнение для воздуха (считаем, что воздух находится в спокойном состоянии)

Вычитая из первого второе, получаем уравнение Бернулли для газа в избыточных давлениях:

Если перейти к ранее принятому обозначению через h, то уравнение можно соответственно переписать в таком виде:

(15¢)

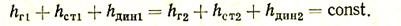
Однако равенство h_S₁ = h_S₂ строго справедливо лишь для идеальной среды, полностью лишенной вязкости. Но если по каналу перемещается реальная (вязкая) жидкость (газ), то часть энергии тратится на преодоление различных сопротивлений и происходит потеря энергии.

В этом случае при движении от сечения I к сечению II

и окончательно закон Бернулли формулируется следующим образом: «При установившемся течении несжимаемой жидкости (газа) для различных сечений канала сумма давлений всех видов является постоянной».

Рассмотрим, что представляет собой потерянное давление, входящее в уравнение Бернулли.

При движении реального газа часть его энергии расходуется на преодоление различных сопротивлений.

Различают потери на трение и потери на преодоление местных сопротивлений. Потери на местные сопротивления возникают при резком изменении величины и направления скорости, при резком изменении сечения канала, при повороте канала или усложнении его сечения (трубчатый пучок). Величину потерь напора выражают в долях динамического давления.

Потери на трение Л_тр можно определить по формуле (Па)

(17)

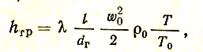
где l — коэффициент трения; l — длина канала, м; d_г— гидравлический диаметр канала, м (для некруглого сечения канала d_г =4F/П, F — площадь сечения канала, м 2 ; П — периметр канала, м); r₀ и w₀ — плотность и скорость жидкости (газа) при нормальных условиях, т. е. при атмосферном давлении и температуре Т₀, равной 273 К; Т — действительная температура жидкости или газа, К.