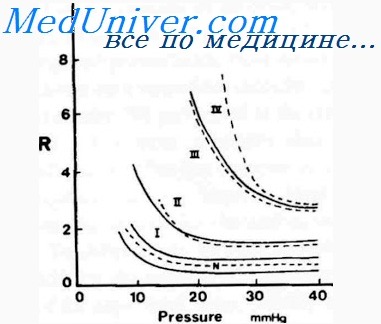
Движение жидкости в замкнутой системе подчиняется закону Бернул-ли, который определяет, что жидкость перемещается из области более высокого давления в область более низкого давления. Исходя из этого, можно заключить, что движущей силой венозного притока является градиент среднего системного давления и давления в правом предсердии.
В физиологии кровообращения под средним системным давлением в сердечно-сосудистой системе понимается давление, которое устанавливается в условиях прекращения кровотока (остановка сердечной деятельности), после того, как перераспределение крови между артериями, капиллярами и венами приведет к выравниванию давления во всех сегментах соответствующего круга кровообращения. Иначе говоря, среднее системное давление отражает усредненный уровень давлений во всех сегментах сердечно-сосудистой системы.
Величина среднего давления в каждом сегменте сердечно-сосудистой системы зависит от его емкости, под которой понимается объем крови, находящейся в этом сегмент при данном уровне давления и описывается следующим отношением:
С = V/P, где
С — емкость сосудистого русла;
V — изменение объема крови;
Р — изменение давления.
Отсюда следует, что при изменении емкости сосудистого русла будет изменяться и среднее системное давление. Чем больше емкость сосудистого русла, тем меньше будет возрастать системное давление при увеличении в нем объема крови. Специальными исследованиями было установлено, что емкость венозного русла в 18 раз больше артериального.
Поэтому венозное русло может депонировать значительные количества крови без существенного повышения в нем давления, а даже незначительный прирост объема крови в артериальной системе неизбежно приведет к возрастанию системного давления. Следовательно, среднее системное давление в сердечно-сосудистой системе представляет собой усредненную величину емкости артериального и венозного русла.
К сожалению, определить среднее системное давление можно только в эксперименте, т.к. для этого необходима остановка сердца. Однако известно, что основные гемодинамические функции у животного (собаки) и человека существенно не различаются и закономерности, установленные в эксперименте, подтверждаются при исследованиях, проведенных у человека при операциях на сердце в условиях искусственного кровообращения.
В связи с этим данные, полученные в эксперименте, в частности относительно закономерностей венозного притока, могут быть с достаточной степенью вероятности экстраполированы на человека.
Так было установлено, что нормальные величины среднего системного давления в большом и малом круге кровообращения различаются незначительно и составляют соответственно 7 мм Нд для большого и 5 мм Нд для малого круга кровообращения. Следовательно, в нормальных условиях (при отсутствии патологии гемодинамики) градиент давлений, обеспечивающий венозный приток, составляет 7-10 мм Нд. И именно в этом диапазоне давлений реализуются нормальный венозный приток и сердечный выброс.
Видео:Закон БернуллиСкачать

«Применим ли закон Бернулли для движения крови по кровеносным сосудам?»
Работа Антроповой Д.А. помогает найти ответ на проблемный вопрос, возникший при попытке применить законы физики к физиологии человека.
Идея работы: объяснить с помощью законов физики движение крови по кровеносным сосудам. Экспериментально доказать, что давление и скорость движения крови в сосудах зависят от площади сечения. Создать модель, которая поможет продемонстрировать эту зависимость. Проверить и объяснить на эксперименте, применим ли закон Бернулли для движения крови по кровеносным сосудам.
Видео:Закон БернуллиСкачать

Скачать:
| Вложение | Размер |
|---|---|
| «Применим ли закон Бернулли для движения крови по кровеносным сосудам?» | 904.34 КБ |
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Предварительный просмотр:
Частное общеобразовательное учреждение «Школа-интернат №22 ОАО «РЖД»
«Применим ли закон Бернулли для движения крови по кровеносным сосудам?»
Автор: Антропова Дарья Андреевна,
10 класс, Школа интернат № 22 ОАО «РЖД»
Научные руководители: Хамаганова Татьяна Фёдоровна,
учитель химии и биологии высшей квалификационной категории,
Школа-интернат №22 ОАО «РЖД»
Максимова Александра Андреевна,
учитель физики 1 квалификационной категории,
Школа-интернат №22 ОАО «РЖД»
Виды кровеносных сосудов, их основные характеристики……….………………..
Физико-биологическое моделирование движения крови по сосудам и возможность применения к ней закона Бернулли.………….………………………..
Анализ полученных данных в результате исследовательской работы ……….……
Список использованных источников………………………………………………………
С точки зрения биологии, движение крови по кровеносным сосудом, это процесс довольно сложный и характеризуется множеством параметров, такими как скорость течения, диаметр сосуда, вязкость крови и т.д. Но возможно ли применить физические законы к этому процессу. Возникнут ли противоречия при попытке применить законы физики к физиологии человека.
Так, в гемодинамике [1] , движение крови по сосудам объясняется такими физическими величинами как давление и скорость движения крови. В гидродинамике данные величины связаны законом Бернулли. Но применим данный закон к движению крови.
Цель эксперимента : выявить зависимость внутреннего давления и скорости движения жидкости от площади поперечного сечения кровеносных сосудов.
Гипотеза: закон Бернулли применим для движения крови по кровеносным сосудам.
Идея проекта: объяснить с помощью законов физики движение крови по кровеносным сосудам. Экспериментально доказать, что давление и скорость движения крови в сосудах зависят от площади сечения. Создать модель, которая поможет продемонстрировать эту зависимость. Проверить и объяснить на эксперименте, применим ли закон Бернулли для движения крови по кровеносным сосудам.
Объект исследования: движение крови по кровеносным сосудам.
Предмет исследования: давление и скорость течения крови.
- изучить литературу по данной теме;
- рассмотреть закономерности в уравнение Бернулли и гемодинамике;
- создать физико-биологическую модель кровеносных сосудов;
- сравнить и проанализировать полученные данные.
Метода исследования : практический эксперимент, посредством моделирования, мыслительно-логические методы, такие как постановка проблемы, сравнение и анализ.
1. Виды кровеносных сосудов, их основные характеристики
Кровообращение — циркуляция крови по организму. Начиная с представителей класса рыб, кровь приводится в движение сокращениями сердца и циркулирует по сосудам. Кровь снабжает ткани организма кислородом, питательными веществами, гормонами и доставляет продукты обмена веществ к органам их выделения. Обогащение крови кислородом происходит в лёгких, а насыщение питательными веществами — в органах пищеварения. Кровообращение регулируется гормонами и вегетативной нервной системой. Различают малый (через лёгкие) и большой (через органы и ткани) круги кровообращения.
Кровообращение — важный фактор в жизнедеятельности организма человека и ряда животных. Кровь может выполнять свои разнообразные функции только находясь в постоянном движении.
Кровеносная система человека и многих животных состоит из сердца и сосудов, по которым кровь движется к тканям и органам, а затем возвращается в сердце. Крупные сосуды, по которым кровь движется к органам и тканям, называются артериями. Артерии разветвляются на более мелкие артерии, артериолы, и, наконец, на капилляры. По сосудам, называемым венами, кровь возвращается в сердце. Сердце четырёхкамерное и имеет два круга кровообращения.
Рис.1 Круги кровообращения
Самые первые количественные измерения механических явлений в кровообращении были сделаны Стивеном Хейлзом (1677—1761 г.), который измерил артериальное и венозное кровяное давление, объём отдельных камер сердца и скорость вытекания крови из нескольких вен и артерий, продемонстрировав таким образом, что большая часть сопротивления течению крови приходится на область микроциркуляции.[1] Он полагал, что вследствие упругости артерий течение крови в венах более или менее установившееся, а не пульсирующее, как в артериях.
Кровообращение человека происходит по трём группам сосудов: артерии, капилляры и вены. Рассмотрим их основные отличительные характеристики.
Основные характеристики сосудов человека:
Артерии, которые почти не содержат гладких мышц, но имеют мощную эластическую оболочку, выполняют главным образом «буферную» роль, сглаживая перепады давлений между систолой и диастолой. Именно растяжение стенки сосуда воспринимается как удар пульса. Артериолы обладают развитой гладкой мускулатурой, благодаря которой способны активно менять свой просвет и, таким образом, регулировать сопротивление кровотоку.
Марчелло Мальпиги, который в 1661 г. открыл капилляры — звено кровеносных сосудов, которое соединяет артерии и вены, — и таким образом завершил описание замкнутой сосудистой системы.[2]
Капилляры характеризуются тем, что их сосудистая стенка представлена одним слоем клеток, так что они высоко проницаемы для всех растворенных в плазме крови низкомолекулярных веществ. Здесь происходит обмен веществ между тканевой жидкостью и плазмой крови.
От органов кровь возвращается через посткапилляры в венулы и вены в правое предсердие по верхней и нижней полым венам, а также по коронарным венам. Гладкие мышцы вен обеспечивают изменение их объёма в весьма широких пределах, приспосабливая их ёмкость к меняющемуся объёму циркулирующей крови. поэтому физиологическая роль вен определяется как «ёмкостные сосуды».
Движение крови по сосудам осуществляется, главным образом, благодаря разности давлений между артериальной системой и венозной. Это утверждение полностью справедливо для артерий и артериол, в капиллярах и венах появляются вспомогательные механизмы. Разность давлений создаётся ритмической работой сердца, перекачивающего кровь из вен в артерии. [3]
2. Закон Бернулли
Закон Бернулли [4] (также уравнение Бернулли, теорема Бернуллиили интеграл Бернулли) устанавливает зависимость между скоростью стационарного потока жидкости и её давлением.
При переходе жидкости с участка трубки с большим сечением на участок с меньшим сечением, скорость течение возрастает. Т.е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке.
Математический вид закона Бернулли выглядит следующим образом:
ρ— плотность жидкости;
υ— скорость потока;
g — ускорение свободного падения [5].
Согласно этому закону, если вдоль линии тока давление жидкости возрастает, то скорость течения убывает, и наоборот.
3. Физико-биологическое моделирование движения крови по сосудам и возможность применения к ней закона Бернулли
Для того, чтобы наглядно продемонстрировать движение крови, я создала модель, состоящую из трубок разного диаметра, где трубка с наименьшим поперечным сечением будет демонстрировать движение крови в капиллярах. А трубка с наибольшим поперечным сечением – движение в аорте. Трубка среднего диаметра – движение в артериях. И к каждой трубке подсоединён жидкостный манометр. Подключаем нашу установку к водопроводной сети под давлением, и проверяем жидкостным манометром давление, создаваемое в трубках разного диаметра.
Для создания модели нам понадобились:
- 3 трубки различного сечения, для демонстрации движения крови в сосудах разного диаметра (аорта, артерии, капилляры);
- 3 манометра, для определения внутреннего давления жидкости в трубке;
- подводящие и отводящие жидкость шланги и переходники;
- стробоскоп, для наблюдения быстрого движения струящейся жидкости из трубки;
- пищевой краситель красного цвета, для демонстрации скорости движения жидкости в трубке.
Рис. 2 Экспериментальная модель кровеносных сосудов
В трубке с наибольшим поперечным сечением манометр показывает 240 мм рт.ст. В трубке с наименьшим поперечным сечением 217 мм рт. ст.. В трубке среднего диаметра — 210 мм. рт. ст. Убираем манометры. Снова подключаем нашу установку к водопроводной сети. И сравниваем высоту фонтанов.
Рис. 3 Разность высот «фонтанов»
Фонтан, образующийся на трубке большего диаметра самый высокий, а самый низкий на трубке меньшего диаметра. Оказалось, что вода быстрее окрашивается в трубке меньшего диаметра.
4. Анализ полученных данных в результате исследовательской работы
Т.к. вода быстрее окрашивается в трубке меньшего диаметра, следовательно, скорость движения воды в ней самая высокая, что противоречит движению крови по кровеносным сосудам. Ведь в капиллярах скорость движения крови меньше, чем артериях, хотя артерии шире. А это имеет огромный биологический смысл, ведь благодаря медленному движению крови по капиллярам в тканях осуществляется газообмен.
Разрешить проблему и разобраться в данном вопросе мне помогла формула Торричелли, не входящая в школьный курс.
— скорость кровотока в сосуде,
S — поперечное сечение кровеносного сосуда.
Данная формула показывает, что линейная скорость кровотока уменьшается по мере увеличения суммарного сечения параллельно соединённых сосудов, т.е. учитывается свойство пропускной способности сосудов . Есть закономерность: циркуляция жидкости выше в том участке, где имеется наименьшее сечение сосуда. Такой участок — аорта. Самый широкий суммарный просвет в капиллярах. Исходя из этого, максимальная скорость в аорте (500 мм/сек), минимальная – в капиллярах (0.5 мм/сек) [6].
Наша гипотеза подтвердилась: уравнение Бернулли применимо к движению крови по кровеносным сосудам. Возникшее противоречие объясняется тем, что в капиллярах скорость движения крови низкая, потому что в капиллярах нашего тела самый широкий суммарный просвет, т.е. суммарная площадь сечения, которая в 1000 раз больше сечения аорты, и приводит к минимальной скорости движения крови в капиллярах.
Проведенные исследования важны с практической точки зрения. Данная модель может быть использована на уроках физики при углублённом изучении гидродинамики, а также на уроках биологии при рассмотрении кровеносной системы человека
Список использованных источников
- Кровообращение. URL: https://ru.wikipedia.org/wiki/
- Котляров С. Н., Александрова Л. Н. История создания шприца // Научная статья в № 2 журнала «Наука молодых — Eruditio juvenium» от 2016 г. — Рязань: Рязанский государственный медицинский университет имени академика И. П. Павлова. С. 41-48. УДК: 615.473.3. ISSN 2311-3820
- Сонин Н.И. Биология: Человек. 8 кл.: учебник /Н.И. Сонин, М.Р. Сапин. – 2-е изд., стереотип. – М.: Дрофа, 2015. – 302, [2] с.
- Ландсберг Г. С. Элементарный учебник физики. Механика. Теплота. Молекулярная физика.// Закон Бернулли / под ред. Г. С. Ландсберга., — М.:Просвещение, 1985. стр. 350 URL: http://mat.net.ua/mat/biblioteka-fizika/Landzberg-fizika-t1-mehanika-teplota.pdf
- Степанова Г.Н. Физика. 10 класс: учебник для 10 класса общеобразовательных учреждений: в 2-х частях. Ч.1. Механика./Г.Н.Степанова. – М.: ООО «ТИД» Русское слово — РС», 2010.-192с.: ил., стр. 158.
- С какой скоростью движется кровь. URL: https://mirinteresen.net/1749-s-kakoy-skorostyu-dvizhetsya-krov.html
[1] Гемодинамика — раздел физиологии кровообращения, рассматривающий закономерности, причины, механизмы и проявления движения крови в сердечно-сосудистой системе.
Видео:Уравнение Бернулли гидравликаСкачать

ЛЕКЦИЯ 4. Уравнения Бернулли и его следствия. Вязкость жидкости. Физические основы гемодинамики
Уравнения Бернулли и его следствия.Линии тока и трубка тока. Условие неразрывности струи.
Течение жидкости изображается линиями тока.
Линия тока— линия, касательные к которым в каждой точке совпадают с направлением вектора скорости частиц. Течение жидкости называется установившимся, стационарным,если скорости частиц в каждой точке потока со временем не изменяются (при этом условии линии тока совпадают с траекториями частиц жидкости).
При стационарном течении линии тока остаются неизменными. Часть потока жидкости, ограниченная линиями тока, образует трубку тока.
Поскольку частицы жидкости не выходят за пределы трубки тока, то через любое ее сечение проходит одно и то же количество жидкости.
Объем Q жидкости, протекающей за единицу времени через любое сечение S, перпендикулярное оси трубки тока, определяется формулой:
Q = S∙υ = const(5.1)
где υ— скорость движения частиц жидкости в данном сечении.
Поскольку, жидкость идеальная и на нее не действию силы трения, то скорости движения частиц во всех точках одного и того же поперечного сечения трубы одинаковы, эта скоростьвходит в уравнение (5.1).
На частицы реальной жидкости действуют силы трения со стороны стенок трубы и со стороны соседних частиц. Поэтому скорость частиц жидкости в поперечном сечении трубы различна: она максимальна в центре трубы и уменьшается до нуля у ее стенок. Входящая в формулу (5.1) будет υ– равная средней скорости течения жидкости в данном сечении.
Уравнение (5.1) выражает условие неразрывности струи. Оно устанавливает соотношение между скоростями течения жидкости в различных сечениях трубки тока:
Условие неразрывности струи:при стационарном течении несжимаемой жидкости через любые сечения трубки тока каждую секунду протекают одинаковые объемы жидкости, равные произведению площади сечения на среднюю скорость движения ее частиц.
Если жидкость движется по трубе переменного сечения, то скорость ее движения обратно пропорциональна площади сечения трубок (рис. 7.1).
Рис. 5.1.Движение жидкости в трубе с разными сечениями. Длина стрелок изображает среднюю скорость течения жидкости.
Площадь сечения пропорциональна квадратудиаметра трубки (S = πd 2 /4), поэтому если диаметр трубки в сечении С вдвоеменьше, чем в сечении А, то площадь поперечного сечения С в четыре раза меньше, чем площадь сечения А. Следовательно, и скорость потока в сечении С будет в четырераза больше, чем в сечении А.
Уравнение неразрывности струи при протекании крови в сосудах
Кровеносная система человека — это сложная замкнутая система эластичных трубок разного диаметра. В нее входят: аорта, артерии, артериолы, капилляры, венулы, вены. Из сердца кровь поступает в аорту, а оттуда распределяется по главным артериям, затем по более мелким и в конце концов расходится по миллионам мелких капилляров. По венам кровь возвращается в сердце. (Один цикл движения крови длится в среднем 20 с. За сутки сердце перегоняет по всем сосудам до 10 000 л крови!) Скорость кровотока в разных сосудах различна. Ориентировочные значения этой скорости представлены в табл. 5.1.
Таблица 5.1.Скорость и давление крови в различных сосудах
На первый взгляд, кажется, что приведенные значения противоречат уравнению неразрывности — в тонких капиллярах скорость кровотока примерно в 1000 меньше, чем в артериях. Однако это несоответствие кажущееся. Дело в том, что в табл. 5.1 приведен диаметр одного сосуда. Эта величина действительно уменьшается по мере разветвления. Однако суммарная площадь разветвления возрастает. Так, суммарная площадь всех капилляров (около 2000 см 2 ) в сотни раз превышает площадь аорты — этим и объясняется такая малая скорость крови в капиллярах. Малая скорость кровотока в капиллярах необходима для обеспечения эффективного обмена между кровью и тканями.
Уравнение Бернулли
Рассмотрим течение идеальной жидкости через тонкую трубку тока разного сечения расположенную под углом.
Выделим в ней два участка разного сечения S1 и S2. Вследствие неразрывности жидкости течение идеальной жидкости в этих сечениях будет с разными скоростями ʋ1 и ʋ2 .
Объем жидкости, протекающей за единицу времени через любое сечение, перпендикулярное оси трубки тока: Q = S1ʋ1 = S2ʋ2 = Sʋ = const,
где S— площадь сечения; ʋ— скорость течения.
Обозначим давления жидкости в этих сечениях Р1 и Р2.
Используя закон сохранения энергии можно доказать, что в этих сечениях выполняется следующее соотношение:
Р1 + ρʋ1 2 /2+ ρgh1 = Р2 + ρʋ2 2 / 
При стационарномтечении идеальной жидкости полное давление, равна сумме статического , динамического и гидростатического давлений, одинаково во всех поперечных сеченияхтрубки тока.
Равенство Р + ρ 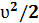
гдеР — статическое давление, которое оказывают друг на друга соседние слои жидкости (его можно измерить манометром, который движется вместе с жидкостью), ρgh — давление, создаваемое весом вертикального столба жидкости высотой h, ρ 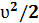
🎬 Видео
Уравнение Бернулли для потока жидкостиСкачать

Применим ли закон Бернулли для движения крови в кровеносных сосудах?Скачать

Уравнение БернуллиСкачать

Галилео. Эксперимент. Закон БернуллиСкачать

Галилео. Эксперимент. Закон БернуллиСкачать

Закон Бернулли и движение по инерцииСкачать

Закон Бернулли в реальной жизниСкачать

Закон БернуллиСкачать

Уравнение БернуллиСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Эффект Магнуса и уравнение БернуллиСкачать

Лайфхак закон БернуллиСкачать

Пульверизатор и закон БернуллиСкачать

10. Уравнения БернуллиСкачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Основы гидродинамики и аэродинамики | условие неразрывностиСкачать