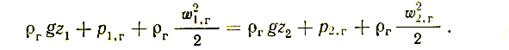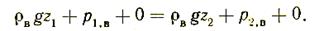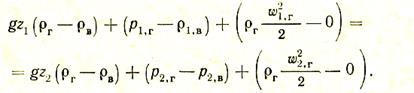Уравнение бернулли для идеального и реального газа (7 видео)

Элементы теории движения реальных газов

При движении газа на каждый его объем будут действовать не только те силы, которые характерны для статики, но и другие, сильно усложняющие как явление в целом, так и его математическое описание. Для движения идеального газа этими дополнительными силами будут силы инерции, а для реального газа — силы инерции и трения (вязкости). В механике сплошных сред большое внимание уделяется выводу и использованию соответствующих математических уравнений, описывающих движение идеальных (уравнения Эйлера) и реальных сред (уравнения Навье — Стокса). Уравнения Навье — Стокса настолько сложны, что к настоящему времени решены лишь для крайне ограниченного числа случаев. Эта сложность вызвана сильным влиянием вязкости среды на различные аспекты процесса движения. В силу этого в допустимых случаях прибегают к решению уравнений Эйлера для движения идеальных сред с введением необходимых поправок и уточнений. Таким образом, получено одно из важнейших уравнений гидро- и аэродинамики — уравнение (закон) Бернулли.

Уравнение Бернулли. В практических условиях крайне распространенным является движение в трубах и каналах, когда газ через боковые стенки не расходуется. В таких случаях для расчетов применяется уравнение Бернулли, полученное для струйки тока (трубка тока), характерной тем, что расход газа в любом ее сечении остается неизменным (обмен газом между всем потоком и струйкой тока через ее боковые границы отсутствует).

Для несжимаемого газа (r = const) уравнение Бернулли при условии, что все его члены отнесены к единице объема, имеет вид

rgz +р +rw 2 /2 = const. (14)

В соответствии сэтим величина р является статическим давлением, величина rgz — геометрическим давлением, величина rw 2 /2 — динамическим давлением.

Уравнение Бернулли представляет собой закон сохранения энергии, поскольку сумма р + rgz характеризует потенциальную, а величина rw 2 /2 — кинетическую энергию.

Как отмечалось выше, в металлургической теплотехнике в подавляющем большинстве случаев пользуются давлением, избыточным над атмосферным. Поэтому полезно уравнение Бернулли привести к такому виду, при котором все члены его были бы выражены в избыточных давлениях. Для этого представим себе канал, окруженный воздухом плотностью r_в, по которому движется газ плотностью r_г. Принимая плотности газа и воздуха неизменными, напишем уравнение Бернулли и для газа и воздуха применительно к сечениям канала z₁и z₂.

Уравнение для газа

Уравнение для воздуха (считаем, что воздух находится в спокойном состоянии)

Вычитая из первого второе, получаем уравнение Бернулли для газа в избыточных давлениях:

Если перейти к ранее принятому обозначению через h, то уравнение можно соответственно переписать в таком виде:

(15¢)

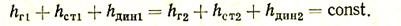
Однако равенство h_S₁ = h_S₂ строго справедливо лишь для идеальной среды, полностью лишенной вязкости. Но если по каналу перемещается реальная (вязкая) жидкость (газ), то часть энергии тратится на преодоление различных сопротивлений и происходит потеря энергии.

В этом случае при движении от сечения I к сечению II

и окончательно закон Бернулли формулируется следующим образом: «При установившемся течении несжимаемой жидкости (газа) для различных сечений канала сумма давлений всех видов является постоянной».

Рассмотрим, что представляет собой потерянное давление, входящее в уравнение Бернулли.

При движении реального газа часть его энергии расходуется на преодоление различных сопротивлений.

Различают потери на трение и потери на преодоление местных сопротивлений. Потери на местные сопротивления возникают при резком изменении величины и направления скорости, при резком изменении сечения канала, при повороте канала или усложнении его сечения (трубчатый пучок). Величину потерь напора выражают в долях динамического давления.

Потери на трение Л_тр можно определить по формуле (Па)

(17)

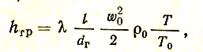
где l — коэффициент трения; l — длина канала, м; d_г— гидравлический диаметр канала, м (для некруглого сечения канала d_г =4F/П, F — площадь сечения канала, м 2 ; П — периметр канала, м); r₀ и w₀ — плотность и скорость жидкости (газа) при нормальных условиях, т. е. при атмосферном давлении и температуре Т₀, равной 273 К; Т — действительная температура жидкости или газа, К.

При ламинарном движении (Rе

Дата добавления: 2015-11-10 ; просмотров: 1211 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Основы гидравлики
Уравнение Бернулли — фундамент гидродинамики
Геометрическая интерпретация уравнения Бернулли
Пример решения задачи на определение расхода жидкости
1 Динамика жидкости и газа Лекционный материал
Главная > Документ
🎦 Видео

Видео:Закон БернуллиСкачать

Основы гидравлики

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнение Бернулли — фундамент гидродинамики

Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S₁ и S₂ , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S₁ скорость течения ν₁ , давление p₁ и высота, на которой это сечение расположено, h₁ . Аналогично, в месте сечения S₂ скорость течения ν₂ , давление p₂ и высота сечения h₂ .

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S₁ к сечению S₁‘ , от S₂ к S₂‘ .

По закону сохранения энергии, изменение полной энергии E₂ — E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

где E₁ и E₂ — полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S₁ и S₂ , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S₁ до S₁‘ жидкость должна переместиться на расстояние L₁ = ν₁Δt и от S₂ до S₂‘ — на расстояние L₂ = ν₂Δt . Отметим, что L₁ и L₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,

где F₁ = p₁S₁ и F₂ = — p₂S₂ (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

Разделив выражение (5) на ΔV , получим

где ρ — плотность жидкости.

После некоторых преобразований эту формулу можно представить в другом виде:

Поскольку сечения выбирались произвольно, то в общем случае можно записать:

ρv 2 /2 +ρgh +p = const (6) .

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 — динамическим давлением, величина ρgh — гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:

ρv 2 /2 + p = const (7) .

Выражение p + ρν 2 /2 называется полным давлением.

Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину h_п = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’_e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить h_f потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:

Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α₁ , α₂ — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α₁ = α₂ = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S₁v₁Δt = S₂v₂Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .

Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая — прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:

Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₁ выхода ее из отверстия) и применим уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁ = р₂ , то уравнение будет иметь вид

Из уравнения неразрывности мы знаем, что ν₁/ν₂ = S₂/S₁ , где S₁ и S₂ — площади поперечных сечений сосуда и отверстия.
Если S₁ значительно превышает S₂ , то слагаемым ν₁ 2 /2 можно пренебречь и тогда:

Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .

Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие — µ_s = 0,62.

По формуле Торричелли определим скорость истечения воды из отверстия:

v = √2gh = √2×10×1 ≈ 4,5 м/с.

Определим расход воды Q за время t = 10 секунд:

Q = µ_svSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .

Видео:Закон БернуллиСкачать

1 Динамика жидкости и газа Лекционный материал

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Уравнение Бернулли для газа

Рассмотрим поток газа, проходящий по трубопроводу переменного сечения (рис. 27). В первом сечении приведённое полное давление равно p пр.п1 . При прохождении по трубе часть p пр.п1 необратимо потеряется из-за проявления сил внутреннего трения газа и во втором сечении энергетическая характеристика уменьшится до p пр.п2 на величину потерь давления D p пот .

Уравнение Бeрнулли для газа в простейшем виде записывается так:

p пр.п1 = p пр.п2 + D p пот ,

то есть это уравнение для двух сечений потока в направлении его движения, выраженное через приведённые полные давления и отражающее закон сохранения энергии (часть энергии переходит в потери) при движении газа.

Уравнение Бeрнулли в традиционной записи получим, если в последнем равенстве раскроем значения приведённых полных давлений p пр.п1 и p пр.п2 :

Энергетический смысл уравнения Бeрнулли для газа заключается в том, что оно отражает закон сохранения энергии, а геометрический не рассматривается, так как величины в нём выражаются в единицах давления ( Па ), а не напора ( м ).

Разность давлений и потери давления

Особенности терминов «разность давлений» и «потери давления » поясним на примерах.

Движение газа происходит только при наличии разности приведённых полных давлений

p пр = p пр.п1 — p пр.п2

от точки с большим давлением p пр.п1 к точке с меньшим p пр.п2 . Например, это является условием работы систем естественной вентиляции зданий: для удаления воздуха из помещения давление p пр.п внутри должно быть больше, чем снаружи.

Потери давления p пот отражают потерю полной энергии потока при движении газа. Например, чем длиннее воздуховод, меньше его проходное сечение, шероховатее его стенки, тем больше будут потери давления в системе вентиляции, что может ухудшить удаление несвежего воздуха из помещений. В покоящемся газе никаких потерь давления нет.

При установившемся движении газа разность давлений равна потерям давления:

p пр = p пот ,

что является уравнением Бернулли в простейшей записи.

Таким образом, «разность давлений » является причиной движения газа, а «потери давления »- следствием. При движении газа они численно равны. Измеряются они в одних и тех же единицах СИ: паскалях ( Па ).

Два режима движения жидкости (газа) .

Исследование вопроса о механизме движения жидкости (газа) показывает, что в природе существуют два вида (режима) движения жидкости: во-первых, слоистое, упорядоченное или ламинарное движение, при котором отдельные слои жидкости скользят друг относительно друга, не смешиваясь между собой, и, во-вторых, неупорядоченное или турбулентное движение, при котором частицы жидкости движутся по сложным, постоянно меняющимся траекториям и в потоке происходит интенсивное перемешивание микро- и макромасс жидкости. Основной особенностью турбулентного режима течения является наличие поперечных к основному направлению движения составляющих скоростей, накладывающихся на основную скорость в продольном направлении.

Выяснению условий существования ламинарного или турбулентного режима течения жидкости, влияния физических характеристик жидкости на переход из одного режима в другой были посвящены опыты Рейнольдса.

Рейнольдс установил, что основными факторами, определяющими характер режима, являются: средняя скорость движения жидкости , диаметр трубопровода , плотность жидкости , абсолютная вязкость , а переход от ламинарного режима к турбулентному происходит при определенной скорости – критической скорости, различной для труб разных диаметров и возрастающей с увеличением вязкости жидкости и уменьшающейся с уменьшением диаметра трубы.

Для характеристики режима движения жидкости Рейнольдсом был выведен безразмерный параметр , учитывающий влияние перечисленных выше факторов и называемый числом (критерием) Рейнольдса

(1.53)

Так как отношение где — коэффициент кинематической вязкости жидкости (газа), то выражение (1.52) можно записать в виде

(1.54)

Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса: нижним критическим числом и верхним критическим числом . При значениях чисел Рейнольдса возможен только ламинарный режим, а при — только турбулентный режим; при наблюдается неустойчивое состояние потока. Таким образом, для определения режима течения необходимо в каждом случае вычислять по выражению (1.53 или 1.54) число Рейнольдса и сопоставлять его с критическим значением.

В опытах самого Рейнольдса значение были следующие: . Последующие эксперименты показали, что критические числа Рейнольдса не являются вполне постоянной величиной и что при определенных условиях неустойчивая зона может быть значительно шире. В настоящее время при практических расчетах принято исходить из одного значения критического числа Рейнольдса, равного , считая, что при всегда имеет место ламинарный режим, а при – всегда турбулентный. При этом движение в неустойчивой зоне исключается из рассмотрения, что приводит к некоторому запасу и большей надежности при гидравлических расчетах в том случае, если в этой зоне в действительности имеет место ламинарный режим течения.

Проведенные исследования особенностей различных режимов движения жидкости показывают, что одновременно с переходом от ламинарного режима к турбулентному изменяется характер распределения скоростей по поперечному сечению потока, а также зависимость потерь энергии (напора). Установлено, что для ламинарного режима характерен параболический закон распределения скоростей по поперечному сечению: скорость жидкости равна нулю непосредственно у стенок трубопровода, а при удалении от них плавно и непрерывно возрастает, достигая максимума на оси трубопровода (рис.3а).

Рисунок 3. Характер распределения скоростей по перечному сечению потока при ламинарном (а) и турбулентном (б) режиме движения.

Турбулентному режиму движения присущ более сложный закон распределения скоростей по поперечному сечению: в пределах большей части поперечного сечения скорость весьма незначительно отличается от максимального значения на оси трубопровода, но при этом начинает резко падать вблизи стенок трубопровода (рис.3б).

Причиной такого более равномерного закона распределения скоростей при турбулентном режиме является наличие поперечных составляющих скоростей частиц жидкости. В результате этого частицы жидкости с большими скоростями на оси потока и с меньшими скоростями на удалении от оси непрерывно сталкиваются, что приводит к выравниванию их скоростей. В тоже время вблизи стенок трубопровода такое взаимное перемещение частиц друг относительно другу нейтрализуется наличием твердой границы (стенки трубопровода), что и обуславливает более интенсивное падение скорости жидкости.

Если обеспечить протекание жидкости по трубопроводу с различной скоростью и замерить при этом величину потерь напора, то графическая зависимость будет иметь следующий вид (рис.4).