Уравнение беллмана формула и смысл на примере задачи о поиске кратчайшего пути на ациклическом графе

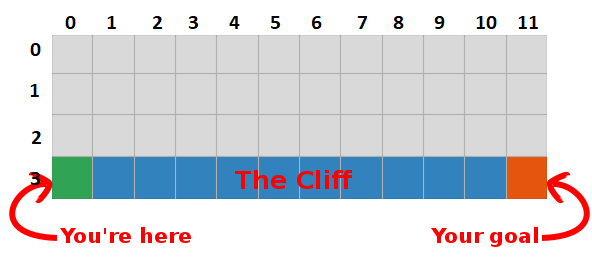
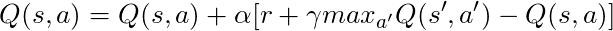В последнем посте мы представили проблему «Прогулка по скале» и остановились на страшном алгоритме, который не имел смысла. На этот раз мы раскроем секреты этого серого ящика и увидим, что это совсем не так страшно.

Резюме

Мы пришли к выводу, что, максимизируя сумму будущих наград, мы также находим самый быстрый путь к цели, поэтому наша цель сейчас — найти способ сделать это!

Введение в Q-Learning

Оптимальная «Q-table» имеет значения, которые позволяют нам предпринимать лучшие действия в каждом состоянии, давая нам в итоге лучший путь к победе. Проблема решена, ура, Повелители Роботов :).

Q-значения первых пяти состояний.

Q-Learning

Например, предположим, что мы на расстоянии одного шага от цели (квадрат [2, 11]), и если мы решим пойти вниз, мы получим вознаграждение 0 вместо -1.
Мы можем использовать эту информацию, чтобы обновить значение пары состояние-действие в нашей таблице, и в следующий раз, когда мы посетим ее, мы уже будем знать, что движение вниз дает нам награду 0.

Теперь мы можем распространить эту информацию еще дальше! Поскольку теперь мы знаем путь к цели из квадрата [2, 11], любое действие, которое приводит нас к квадрату [2, 11], также будет хорошим, поэтому мы обновляем Q-значение квадрата, которое приводит нас к [2, 11], чтобы быть ближе к 0.

И это, леди и джентльмены, и есть суть Q-learning!

Обратите внимание, что каждый раз, когда мы достигаем цели, мы увеличиваем нашу «карту» того, как достичь цели на один квадрат, поэтому после достаточного количества итераций у нас будет полная карта, которая покажет нам, как добраться до цели из каждого состояния.

Путь генерируется путем принятия лучших действий в каждом состоянии. Зеленая тональность представляет значение лучшего действия, более насыщенные тональности представляют более высокие значения. Текст представляет значение для каждого действия (вверх, вниз, вправо, влево).

Уравнение Беллмана

Прежде чем говорить о коде, давайте поговорим о математике: основная концепция Q-learning, уравнение Беллмана.

• Сначала давайте забудем γ в этом уравнении
• Уравнение утверждает, что значение Q для определенной пары состояние-действие должно быть наградой, полученной при переходе в новое состояние (путем выполнения этого действия), добавленной к значению наилучшего действия в следующем состоянии.

Другими словами, мы распространяем информацию о значениях действий по одному шагу за раз!

Но мы можем решить, что получение награды прямо сейчас более ценно, чем получение награды в будущем, и поэтому у нас есть γ, число от 0 до 1 (обычно от 0,9 до 0,99), которое умножается на награду в будущем, обесценивая будущие награды.

Итак, учитывая γ = 0,9 и применяя это к некоторым состояниям нашего мира (сетки), мы имеем:

Мы можем сравнить эти значения с приведенными выше в GIF и увидеть, что они одинаковы.

Реализация

Теперь, когда у нас есть интуивное представление о том, как работает Q-learning, мы можем начать думать о реализации всего этого, и мы будем использовать псевдокод Q-learning из книги Саттона в качестве руководства.

Псевдокод из книги Саттона.

• Во-первых, мы говорим: «Для всех состояний и действий инициализируем Q (s, a) произвольно», это означает, что мы можем создать нашу таблицу Q-значений с любыми значениями, которые нам нравятся, они могут быть случайными, они могут быть какими-то постоянными, не имеет значения. Мы видим, что в строке 2 мы создаем таблицу, полную нулей.

Мы также говорим: «Значение Q для конечных состояний равно нулю», мы не можем предпринимать никаких действий в конечных состояниях, поэтому мы считаем значение для всех действий в этом состоянии равным нулю.

• Для каждого эпизода мы должны «инициализировать S», это просто причудливый способ сказать «перезагрузить игру», в нашем случае это означает поставить игрока в исходное положение; в нашем мире есть метод, который делает именно это, и мы вызывая его в строке 6.
• Для каждого временного шага (каждый раз, когда нам нужно действовать) мы должны выбрать действие, полученное из Q.

Помните, я говорил «мы предпринимаем действия, которые имеют наибольшую ценность в каждом состоянии?

Когда мы делаем это, мы используем наши Q-values для создания политики; в этом случае это будет жадная политика, потому что мы всегда предпринимаем действия, которые, по нашему мнению, лучше всего в каждом состоянии, поэтому говорится, что мы действуем жадно.

Барахление

Но с этим подходом есть проблема: представьте, что мы находимся в лабиринте, у которого есть две награды, одна из которых +1, а другая +100 (и каждый раз, когда мы находим одну из них, игра заканчивается). Так как мы всегда предпринимаем действия, которые считаем лучшими, то мы застрянем с первой найденной наградой, всегда возвращаясь к ней, поэтому, если мы сначала узнаем награду +1, то мы упустим большую награду +100.

Решение

Нам нужно убедиться, что мы достаточно изучили наш мир (это удивительно трудная задача). Вот где вступает в игру ε. ε в жадном алгоритме означает, что мы должны действовать жадно, НО делать случайные действия в процентном соотношении ε по времени, таким образом, при бесконечном количестве попыток мы должны исследовать все состояния.

Действие выбирается в соответствии с этой стратегией в строке 12, с epsilon = 0.1, что означает, что мы занимаемся исследованиями мира 10% времени. Реализация политики осуществляется следующим образом:

В строке 14 в первом листинге мы вызываем метод step для выполнения действия, мир возвращает нам следующее состояние, награду и информацию об окончании игры.

Вернемся к математике:

У нас есть длинное уравнение, давайте подумаем о нем:

Если мы примем α = 1:

Что в точности совпадает с уравнением Беллмана, которое мы видели несколько абзацев назад! Так что мы уже сейчас знаем, что это строка, ответственная за распространение информации о значениях состояний.

Но обычно α (в основном известная как скорость обучения) намного меньше 1, его основная цель — избежать больших изменений в одном обновлении, поэтому вместо того, чтобы лететь в цель, мы медленно приближаемся к ней. В нашем табличном подходе установка α = 1 не вызывает никаких проблем, но при работе с нейронными сетями (подробнее об этом в следующих статьях) все может легко выйти из-под контроля.

Глядя на код, мы видим, что в строке 16 в первом листинге мы определили td_target, это значение, к которому мы должны приблизиться, но вместо прямого перехода к этому значению в строке 17 мы вычисляем td_error, мы будем использовать это значение в сочетании со скоростью обучения, чтобы медленно двигаться к цели.

Помните, что это уравнение является сущностью Q-Learning.

Теперь нам просто нужно обновить наше состояние, и все готово, это строка 20. Мы повторяем этот процесс, пока не достигнем конца эпизода, умирая в скалах или достигая цели.

Заключение

Теперь мы интуитивно понимаем и знаем, как кодировать Q-Learning (по крайней мере, табличный вариант), обязательно проверьте весь код, использованный для этого поста, доступный на GitHub.

Визуализация испытания процесса обучения:

Обратите внимание, что все действия начинаются со значения, превышающего его окончательное значение, это хитрость для стимулирования исследований мира.

Видео:Алгоритм ДейкстрыСкачать

Принцип оптимальности и уравнение Р. Беллмана

Принцип оптимальности Р. Беллмана сформулирован для решения широкого круга задач управления, планирования производственной деятельности, распределения различного рода ресурсов, конструирования, проектирования и др. и вообще для задач принятия решений в многошаговых (многоэтапных) процессах.

Если заданы начальное (точка А) и конечное (точка В) состояния некоторой системы, и переход из начального в конечное состояние осуществляется в несколько промежуточных этапов, на каждом из которых система может находиться в одном из нескольких состояний, и каждому переходу на каждом этапе можно сопоставить некоторые затраты (или прибыль), то задача состоит в том, чтобы выбрать такой путь (то есть все промежуточные состояния), для которого суммарные затраты достигают минимума (или прибыль -максимума). Предположим, что количественная оценка пути это суммарные затраты (сумма затрат по этапам, т.е. сумма шаговых затрат). Пусть на первом этапе из начального состояния (точка А) можно перейти в некоторое конечное число состояний (условно это четыре точки на вертикали 1 рис. 3.5) с соответствующими затратами. Далее, аналогично, из состояний первого этапа (результатов первого шага) можно перейти в конечное число состояний (три точки на вертикали 2) и т.д., вплоть до конечного этапа, на котором из всех возможных состояний возможен переход только в одно конечное состояние (точка В).

В конкретной задаче может быть так, что для каждого или некоторых промежуточных состояний (например, точка С) дальнейшие переходы зависят от того каким образом система была переведена в это состояние (например, переход CD возможен, если пришли в точку С из точки М, и невозможен, если пришли в точку С из точки N). Но может быть и так, что для всех промежуточных состояний дальнейшие переходы и соответствующие затраты никак не зависят от того как система попала в это состояние.

В первом случае говорят о задачах с предысторией, а во втором случае об отсутствии предыстории, точнее о том, что предыстория не имеет значения для дальнейшего поведения системы.

Рис. 3.3. Схема поэтапного поиска оптимального пути

Принцип Р.Веллмана гласит: если в каждом из состояний дальнейшее поведение системы не зависит от того, как она попала в это состояние, то дальнейшая траектория должна быть оптимальной.

Под траекторией понимается последовательность состояний (или переходов), в которых находится система, начиная с первого и до последнего. Если состояние системы определяется координатами некоторой точки (например, центра тяжести движущегося объекта) на плоскости или в обычном трёхмерном пространстве, то это понятие совпадает с привычным понятием траектории. В других задачах состояние системы характеризуется набором чисел, которые можно считать координатами вектора в некотором многомерном пространстве и, следовательно, говорить о траектории в этом пространстве.

Приведенная формулировка принципа оптимальности означает, что речь идёт только о системах «без предыстории». В этом случае из каждого промежуточного состояния можно отдельно, независимо от пройденных этапов, решать задачу поиска оптимального пути в конечное состояние. Или, что фактически то же самое, сравнивать и отбраковывать варианты достижения любого промежуточного состояния из начальной точки и оставлять только один вариант. Это означает возможность применения принципа оптимальности в несколько ином виде: если в каждом из состояний дальнейшее поведение системы не зависит от того, как она попала в это состояние, то это состояние должно достигаться по оптимальной траектории.

В отличие от рассмотренной нами простой задачи поиска оптимального пути на двумерной сетке в сложных задачах каждое промежуточное состояние может определяться не двумя, а многими координатами, то есть каждому состоянию может соответствовать вектор многомерного пространства. От того как формально определено понятие «состояние», зависит не только формализация понятия «переход в другое состояние», но и, как мы увидим в дальнейшем, сама возможность применения метода Р. Веллмана.

Итак, пусть в каждом из состояний, в котором может находиться система в начале очередного этапа, известны все возможные воздействия на неё. И для каждого такого воздействия известны его последствия, то есть и состояние, в которое перейдёт система, и затраты на этот переход. Воздействие на i-ом шаге обозначим через Xi. Эти воздействия называются шаговыми управлениями. Если число этапов обозначить через п, то задача состоит в поиске последовательности шаговых управлений, то есть вектора x(xi,X2. x_n). Поскольку начальное состояние системы задано, то последовательность шаговых управлений однозначно определяет последовательность переходов системы из одного состояния в другое, то есть траекторию движения (в широком смысле слова). В сложных задачах xi,X2. x_n не обязательно числа. Это могут быть векторы или функции.

Обозначим затраты на i-ом этапе через z. Требуется найти такую последовательность шаговых управлений Xi, при которой суммарные затраты Z минимальны.

Ту последовательность шаговых управлений, при которой достигается минимум затрат Z, будем называть оптимальным управлением и обозначать через

[6]. Соответствующие ей минимальные по всем возможным последовательностям х затраты

Затраты на i-ом шаге (этапе) зависят не только от Xi, но и от состояния S, в котором была система до воздействия Xi, то есть фактически от всех предшествующих шаговых управлений. Состояние S’, в которое перейдёт система, зависит только от S и Xi, если нет влияния предыстории. Формально это можно записать в виде S’ =f(S, Xi), где f заданная функция, так как известны последствия воздействия Xi на систему, находящуюся в состоянии S. В соответствии с принципом оптимальности Xi надо выбирать так, чтобы суммарные затраты на все последующие этапы были минимальны. Эти суммарные затраты зависят от состояния S и складываются из затрат на i-ом шаге Zi(S, Xi) и на всех последующих шагах. Суммарные затраты на все шаги (этапы), начиная с i-ro и до конца, обозначим Zi. Тогда Zi=Zi + Zi+i и оптимальные управления надо на каждом шаге выбирать так, чтобы

Это и есть основное рекуррентное уравнение динамического программирования, выражающее затраты на все оставшиеся шаги из любого состояния S через затраты на данном шаге Zi и на всех последующих шагах Zi+i(S’). Только на последнем шаге из любого состояния S можно легко найти оптимальный переход в конечное состояние. Если конечное состояние единственное, то и для каждого из состояний S на последнем шаге этот переход (то есть шаговое управление х_п) единственное. В общем случае для последнего шага уравнение (3.1) приобретает вид

так как п+1 шага просто нет. Это означает, что для каждого из возможных состояний на последнем шаге мы определяем и запоминаем затраты на этот последний шаг. Если конечных состояний несколько (рис. 3.6), то на последнем шаге придётся сравнивать варианты переходов из каждого состояния 1,2. к в конечные состояния Bi,B2. B_m, то есть шаговые управления х_п, обеспечивающие переходы 1 Bi, 1В2,___, 1 B_m, и запоминать наилучшее управление и соответствующие ему минимальные затраты на последний шаг для состояния 1, затем все переходы из состояния 2 и т.д. В результате для каждого состояния S на последнем шаге станут известны затраты Z_n(S) и управление х_п, обеспечивающее оптимальный переход в конечное состояние.

Рис. 3.6 Последний шаг при нескольких конечных состояниях

Запишем теперь уравнение для предпоследнего шага i = n -1.

Здесь затраты уже известны, а найти надо x_n-i для каждого

состояния S на п-1 шаге. Это задача полностью аналогична той, что мы решали для последнего шага. Последовательно, рассматривая шаги от п-1 до 2, определим для каждого из состояний наименьшие затраты на все последующие этапы и управления (переходы на следующий этап). На первом шаге теперь известны последствия любого из возможных переходов (управлений), что и даёт возможность сделать окончательный выбор управления xi, то есть перехода из точки А.

Если начальных состояний (точек А) несколько, то из каждого из них выбирается наилучший переход (управление) и определяются соответствующие минимальные затраты. Затем сравниваются начальные состояния, и выбирается то из них, для которого суммарные затраты минимальны. Таким образом, при любом числе начальных состояний становятся известными и суммарные минимальные затраты на все этапы. Затем обратным разворотом можем найти оптимальную последовательность шаговых управлений (переходов в следующее состояние), если мы запоминали для каждого промежуточного состояния оптимальный переход из него.

Отметим, что поиск оптимального перехода из заданного состояния на i-ом шаге (в том числе и на последнем) может быть сложнее, чем выборка чисел из заданного массива, суммирование и сравнение. В сложных задачах использование принципа оптимальности Р. Веллмана может приводить к разностным, дифференциальным и др. уравнениям.

Часто принцип оптимальности Р.Веллмана формулируют следующим образом: «Оптимальная траектория состоит из оптимальных частей.» Эта формулировка относится не только к траекторным задачам, но ко всем задачам, решаемым с помощью метода динамического программирования, если под траекторией понимать последовательность переходов из одного состояния в другое в результате решений (управлений), принимаемых на последовательных этапах. Если под частью траектории понимать любую последовательность состояний, в которой начальное и конечное состояния фиксированы (аналог кривой, соединяющей две фиксированные точки), то для оптимальной траектории в задачах «без предыстории» это безусловно так. Но это не означает, что для двух состояний ( на этапах р и q рис. 3.7 состояния С и D), которые не содержатся в оптимальной последовательности, то есть не принадлежат оптимальной траектории, не может быть последовательности переходов с меньшими затратами, чем для оптимальной последовательности на тех же промежуточных этапах с р-го по q -ый. На рис. 3.7 для части С* D* оптимальной траектории (показана стрелками) на этапах с р-го по q-ый затраты (4+1+2) больше, чем для части неоптимальной траектории CD на тех же этапах (3+1+1), но в целом суммарные затраты на все этапы для оптимальной траектории меньше (10 против 15).

Смысл метода в том, что из начального состояния в любое промежуточное состояние (точку) нужно идти по оптимальному пути (остальные отбраковываются) и до конечной точки тоже нужно идти по оптимальному пути.

Управления Xi в оптимальной последовательности управлений являются условно оптимальными, так как они выбирались для конкретных состояний с учётом последствий (затрат на все последующие этапы).

Рис. 3.7. Сравнение траекторий

Еще раз подчеркнём, что метод оптимизации Р. Веллмана и соответственно уравнение 3.1 не универсальны и рассмотрим более подробно условия их применимости.

Видео:Алгоритм Дейкстры или как навигатор определяет оптимальный маршрутСкачать

Усиление обучения: Марков-процесс принятия решений (часть 2)

Дата публикации Aug 30, 2019

Эта история в продолжение предыдущего,Усиление обучения: Марков-процесс принятия решений (часть 1)история, в которой мы говорили о том, как определять MDP для данной среды. Мы также говорили о уравнении Беллмана, а также о том, как найти функцию Value и функцию Policy для состояния.В этой историимы собираемся сделать шагГлубжеи узнать оУравнение ожиданий Беллманакак мы находимоптимальное значениеа такжеОптимальная функция политикидля данного состояния, а затем мы определимУравнение оптимальности Беллмана,

Давайте кратко рассмотрим эту историю:

• Уравнение ожиданий Беллмана
• Оптимальная политика
• Уравнение Беллмана для функции состояния
• Уравнение оптимальности Беллмана для функции значения состояния-действия

Так что, как всегда, берите свой кофе и не останавливайтесь, пока вы не гордитесь ».

Давайте начнем с,Что такое уравнение ожидания Беллмана?

Видео:Алгоритм Дейкстры. САМОЕ ПОНЯТНОЕ ОБЪЯСНЕНИЕСкачать

Уравнение ожиданий Беллмана

Быстрый обзорУравнение Беллманамы говорили в предыдущей истории:

Из вышесказанногоуравнениемы можем видеть, что значение состояния может бытьразложившийсяв немедленное вознаграждение (R [T + 1])плюсзначение государства-преемника (v [S (t + 1)]) с учетом скидки (γ). Это все еще означает уравнение ожиданий Беллмана. Но теперь то, что мы делаем, мы находим ценность определенного государстваподвергаетсяк какой-то политике (π). В этом разница между уравнением Беллмана и уравнением ожиданий Беллмана.

Математически мы можем определить уравнение ожиданий Беллмана как:

Давайте назовем это уравнение 1. Вышеупомянутое уравнение говорит нам, что ценность определенного состояния определяется немедленным вознаграждением плюс значение состояний-преемников, когда мы следуем определенной политике (π),

Точно так же мы можем выразить нашу функцию Value-action-состояния (Q-Function) следующим образом:

Давайте назовем это уравнение 2. Из приведенного выше уравнения мы можем видеть, что значение состояния-действия состояния может быть разложено нанемедленная наградамы выполняем определенное действие в состоянии (s) и переезд в другое состояние (s’) плюс дисконтированная стоимость состояния-действия государства (s’)в отношениинекоторые действия ( ) наш агент возьмет из этого штата подопечных.

Идем глубже в уравнение ожиданий Беллмана:

Во-первых, давайте разберемся с уравнением ожидания Беллмана для функции состояния-состояния с помощью резервной диаграммы:

Эта резервная диаграмма описывает значение нахождения в определенном состоянии. Из состояния s есть некоторая вероятность того, что мы предпримем оба действия. Для каждого действия существует Q-значение (функция значения действия состояния). Мы усредняем Q-значения, которые говорят нам, насколько хорошо быть в определенном состоянии. В основном, это определяет Vπ (s). [Смотрите уравнение 1]

Математически мы можем определить это следующим образом:

Это уравнение также говорит нам о связи между функцией State-Value и функцией Value-Action Value.

Теперь давайте посмотрим на схему резервного копирования для функции значения состояния-действия:

Эта резервная диаграмма говорит, что предположим, что мы начнем с некоторых действий (а). Таким образом, из-за действия (а) агент может попасть в любое из этих состояний окружающей средой. Поэтому мы задаем вопрос,Насколько хорошо действовать (а)?

Мы снова усредняем значения состояний обоих состояний, добавленные с немедленной наградой, которая говорит нам, насколько хорошо выполнить определенное действие (а). Это определяет наш qπ (S, A).

Математически мы можем определить это следующим образом:

где P — вероятность перехода.

Теперь давайте соединим эти резервные диаграммы вместе, чтобы определить функцию состояния-значения, VП (с):

Из приведенной выше диаграммы, если наш агент в какой-тосостояния)и из этого состояния предположим, что наш агент может предпринять два действия, в зависимости от того, какая среда может перевести нашего агента в любую изсостояния (s’), Обратите внимание, что вероятность действий, которые наш агент может предпринять из штатаsвзвешивается нашей политикой и после принятия этого действия вероятность того, что мы приземлимся в любом из государств (s’) взвешивается окружающей средой

Теперь мы задаемся вопросом: насколько хорошо быть в состоянии (ях) после того, как вы предприняли какие-то действия и приземлились в другом (ых) государстве (ах) и следовали нашей политике (π) после того?

Это похоже на то, что мы делали раньше, мы собираемся усреднить значение преемников (s’) с некоторой вероятностью перехода (P), взвешенной с нашей политикой.

Математически мы можем определить это следующим образом:

Теперь, давайте сделаем то же самое для функции значения состояния действия, qπ (S, а):

Это очень похоже на то, что мы сделали вФункция значения состоянияи только она обратная, так что эта диаграмма в основном говорит о том, что наш агент предпринял какие-то действия ( ) из-за которого окружающая среда может посадить нас в любом из государств (s), то из этого состояния мы можем выбрать любые действия (а») взвешены с вероятностью нашей политики (π). Опять же, мы усредняем их вместе, и это дает нам понять, насколько хорошо предпринимать определенные действия в соответствии с определенной политикой (π) все это время.

Математически это можно выразить как:

Итак, вот как мы можем сформулировать уравнение ожиданий Беллмана для данного MDP, чтобы найти его функцию значения состояния и функцию значения состояния.Но это не говорит нам лучший способ вести себя в MDP, Для этого давайте поговорим о том, что подразумевается подОптимальное значениеа такжеОптимальная функция политики,

Видео:BP2-3-3-08 Алгоритм Форда-БеллманаСкачать

Функция оптимального значения

Определение оптимальной функции состояния-значения

В среде MDP существует много различных функций-значений в соответствии с различными политиками.Функция оптимального значения — это та, которая дает максимальное значение по сравнению со всеми другими функциями значения., Когда мы говорим, что решаем MDP, это фактически означает, что мы находим функцию оптимального значения.

Итак, математически оптимальная функция состояния-значения может быть выражена как:

В приведенной выше формуле v ∗ (s) говорит нам, какое максимальное вознаграждение мы можем получить от системы.

Определение функции оптимального значения состояния-действия (Q-функция)

По аналогии,Функция оптимального значения состояния-действияговорит нам максимальное вознаграждение, которое мы собираемся получить, если мы находимся в состоянии s и предпринимаем соответствующие действия.

Математически, это может быть определено как:

Оптимальная функция состояния-значения: Это функция максимального значения для всех политик.

Функция оптимального значения состояния-действия: Это функция максимального значения действия для всех политик.

Теперь давайте посмотрим, что подразумевается под Оптимальной политикой?

Видео:Принцип оптимальности БеллманаСкачать

Оптимальная политика

Прежде чем мы определим оптимальную политику, давайте знать,что подразумевается под одной политикой лучше, чем с другой политикой?

Мы знаем, что для любого MDP существует политика (π)лучше любой другой политики (π»). Но как?

Мы говорим, что одна политика (π)лучше другой политики (π») если значение функции с политикойπдля всех состояний больше значения функции с политикойπ»для всех государств. Интуитивно это можно выразить как:

Теперь давайте определимсяОптимальная политика:

Оптимальная политикаэто тот, который приводит к функции оптимального значения.

Обратите внимание, что в MDP может быть более одной оптимальной политики. Но,все оптимальные политики достигают одной и той же функции оптимального значения и функции значения оптимального состояния-действия (Q-функция),

Теперь возникает вопрос, как мы находим оптимальную политику.

Нахождение оптимальной политики:

Мы находим оптимальную политику путем максимизацииQ*(s, a), т.е. наша оптимальная функция значения состояния-действия. Мы решаем q * (s, a) и затем выбираем действие, которое дает нам наиболее оптимальную функцию значения состояния-действия (q * (s, a)).

Вышеприведенное утверждение может быть выражено как:

Это говорит о том, что для состояния s мы выбираем действие a с вероятностью 1, если оно дает нам максимум q * (s, a). Таким образом, если мы знаем q * (s, a), мы можем получить из него оптимальную политику.

Давайте разберемся с этим на примере:

В этом примере красные дуги являютсяоптимальная политикаэто означает, что если наш агент пойдет по этому пути, он будетприносить максимальное вознаграждениеиз этого МДП. Кроме того, увидевд *значения для каждого состояния мы можем сказать действия нашего агента, которые принесут максимальное вознаграждение. Таким образом, оптимальная политика всегда действует с более высоким значением q * (функция значения состояния-действия). Например, в состоянии со значением 8 есть q * со значениями 0 и 8. Наш агент выбирает тот, у которого большед *значение то есть 8.

Теперь возникает вопрос,Как мы находим эти значения q * (s, a)?

Именно здесь в игру вступает уравнение оптимальности Беллмана.

Видео:Кратчайшие пути в ациклических ориентированных графахСкачать

Уравнение оптимальности Беллмана

Функция оптимального значения рекурсивно связана с уравнением оптимальности Беллмана

Уравнение оптимальности Беллмана такое же, как и уравнение ожиданий Беллмана, но единственное отличие состоит в том, что вместо того, чтобы брать среднее значение действий, которые может выполнить наш агент, мы выполняем действие с максимальным значением.

Давайте разберемся с помощью диаграммы резервного копирования:

Предположим, наш агент находится в состоянии S, и из этого состояния он может выполнить два действия (a). Итак, мы смотрим на значения действий для каждого из действий иВ отличие от, Уравнение ожиданий Беллмана,вместоприниматьсреднийнаш агент принимает меры сбольшее значение q *, Это дает нам ценность быть в состоянии S.

Математически это можно выразить как:

Аналогично, давайте определим уравнение оптимальности Беллмана дляФункция значения состояния состояния (Q-функция),

Давайте посмотрим на схему резервного копирования для функции значения состояния-действия (Q-функция):

Предположим, наш агент совершил действие a в каком-то состоянии s. Теперь, на окружающей среде, что это может взорвать нас в любое из этих государств (s’). Мы по-прежнему берем среднее значение обоих государств, но единственноеразницанаходится в уравнении оптимальности Беллмана мы знаемоптимальные значениякаждого из состояний. В отличие от уравнения ожиданий Беллмана, мы просто знали значение состояний.

Математически это можно выразить как:

Давайте снова сшиваем эти резервные диаграммы для функции состояния-значения:

Предположим, наш агент находится в состоянии s, и из этого состояния он предпринял какое-то действие (a), когда вероятность совершения этого действиявзвешенныйполитикой. И из-за действия (а), агент может быть взорван в любом из состояний (s’) где вероятность взвешена окружающей средой.Чтобы найти значение состояния S, мы просто усредняем оптимальные значения состояний (s ’)., Это дает нам ценность пребывания в состоянии S.

Математически это можно выразить как:

Максимум в уравнении потому, что мы максимизируем действия, которые агент может предпринять в верхних дугах. Это уравнение также показывает, как мы можем связать функцию V * с самим собой.

Теперь давайте посмотрим на уравнение оптимальности Беллмана для функции значения состояния-действия, q * (s, a):

Предположим, наш агент был в состоянииsи потребовалось какое-то действие ( ). Из-за этого действия окружающая среда может высадить нашего агента в любой из штатов (s’) и из этих состояний мы получаемразворачиваниядействие, которое предпримет наш агент, то есть выбор действия смаксимальное значение q *, Мы поддерживаем это до самого верха, и это говорит нам о значении действия a.

Математически это можно выразить как:

Давайте посмотрим на пример, чтобы понять его лучше:

Посмотрите на красные стрелки, предположим, что мы хотим найтиценностьсостояния со значением 6 (в красном), как мы видим, мы получаем вознаграждение -1, если наш агент выбирает Facebook, и вознаграждение -2, если наш агент хочет учиться. Чтобы найти значение состояния в красном, мы будем использоватьУравнение Беллмана для функции состояниято естьучитывая, что два других состояния имеют оптимальное значение, мы возьмем среднее значение и максимизируем оба действия (выберите то, которое дает максимальное значение), Таким образом, из диаграммы мы можем видеть, что переход на Facebook дает значение 5 для нашего красного состояния, а при обучении — значение 6, а затем мы максимизируем два, что дает нам 6 в качестве ответа.

Теперь, как мы решаем уравнение оптимальности Беллмана для больших MDP. Для этого мы используемАлгоритмы динамического программированиянравитсяИтерация политикиЗначение итерации, которую мы рассмотрим в следующем рассказе и другие методы, такие какQ-Learningа такжеSarsaкоторые используются для изучения временных различий, о которых мы расскажем в будущем.

Поздравляю с таким большим успехом! 👍

Надеюсь, что эта история повышает ценность вашего понимания MDP. Хотелось бы связаться с вами на #Instagram,

Спасибо, что поделились со мной своим временем!

Если вам нравится этот, пожалуйста, дайте мне знать, нажав на 👏. Это помогает мне писать больше!

💥 Видео

Алгоритм Форда-Беллмана и SPFAСкачать

Теория графов: Волновой алгоритм поиска кратчайшего пути. Центр онлайн-обучения «Фоксфорд»Скачать

Алгоритм поиска кратчайшего пути Форда-БеллманаСкачать

Графы: Алгоритм Форда БеллманаСкачать

АЛГОРИТМ БЕЛЛМАНА-ФОРДА — ИДЕЯ И РЕАЛИЗАЦИЯ (ЧАСТЬ 1)Скачать

ГрафыСкачать

Алгоритмы (базовый поток) 10. Алгоритм Дейкстры, Форда-БеллманаСкачать

Алгоритмы и структуры данных 9. Продолжение кратчайших путей. А*, Флойд, Форд-БеллманСкачать

Поиск пути в играх. Алгоритм поиска пути A*Скачать

Динамическое программированиеСкачать

Задача о кратчайших путях. Алгоритмы Беллмана-Форда, Флойда, Дийкстры и ДжонсонаСкачать

Графы, вершины, ребра, инцидентность, смежностьСкачать

ДС Алгоритм Беллмана-ФордаСкачать

Насыщение сетиСкачать