Уравнение беллмана для дискретных систем (3 видео)

Содержание

Фронтендер пишет нейронки. Уровень сложности «мартышка и уравнение Беллмана»
Метод динамического программирования Р. Беллмана. Принцип оптимальности
Усиление обучения: Марков-процесс принятия решений (часть 2)
Уравнение ожиданий Беллмана
Функция оптимального значения
Оптимальная политика
Уравнение оптимальности Беллмана
🔥 Видео

Видео:МатЭк 8О-406б Динамическое программирование, метод Беллмана СеминарСкачать

Фронтендер пишет нейронки. Уровень сложности «мартышка и уравнение Беллмана»

Количество плюсов под последней статьей говорит о том, что моя подача материала про нейронные сети не вызвала сильного отторжения, поэтому решение — “прочитать, посмотреть что-то новое и сделать новую статью” не заставило себя ждать. Хочется сделать оговорку, что нисколько не претендую на звание того, кто будет учить чему-то и говорить о чем-то серьезном в своей статье. Наоборот, нахожу данный формат — написание статьи или выступление на конференции, способом, когда самому можно чему-нибудь научиться. Ты делаешь что-то, собираешь обратную связь, делаешь что-то лучше. Также это происходит и в нейронных сетях. Кстати о них.

В комментариях к прошлой статье поднялся вопрос про reinforcement learning. Почему бы и нет. Давайте подробнее рассмотрим что это такое.

Как и в прошлый раз, я постараюсь не использовать сложные математические формулы и объяснения, так как сам понимаю на своем примере, что нежные ушки и глазки фронтендера к этому не приспособлены. И как завещал Хокинг, любая формула в популярной работе сокращает аудиторию вдвое, поэтому в этой статье она будет всего одна — уравнение Беллмана, но это уже понятно из названия.

Итак, reinforcement learning, или обучение с подкреплением — это такая группа методов машинного обучения, подходы которой сначала выглядят как методы обучения без учителя, но со временем (время обучения) становятся методами обучения с учителем, где учителем становится сама нейронная сеть. Скорее всего, ничего непонятно. Это не страшно, мы все рассмотрим на примере.

Представим, у нас есть крысиный лабиринт и маленькая лабораторная крыса. Наша цель — научить крысу проходить лабиринт от начала до конца. Но этот лабиринт необычный. Как только крыса, бегая по лабиринту, сворачивает не туда, ее начинает бить током пока она не вернется на правильную дорожку (довольно жестоко, но такова наука). Если же крыса находит конечную точку, то ей дают некоторое кол-во сыра, вознаграждая ее труды.

Наш условный лабиринт

Представляя эту картину, мы можем увидеть все основные составляющие любого проекта с использованием обучения с подкреплением. Во-первых, у нас есть крыса — Агент (agent), наша нейронная сеть, которая мыслит и принимает решения. Во-вторых, у нас есть Окружение или среда (environment) агента — лабиринт, который имеет свое Состояние (state), расположение проходов, мест с котами, финальный островок и так далее. Крыса может принимать решения и совершать определенные Действия (actions), которые могут приводить к разным последствиям. Крыса либо получает Вознаграждение (reward), либо Санкции (penalty or -reward) за свои действия.

Наверное, очевидно, что основной целью является максимизировать свое вознаграждение минимизируя санкции. Для этого нужно принимать правильные решения, а для этого нужно правильно интерпретировать свое окружение. Собственно, для этих задач и пригодилось машинное обучение.

Но, говоря, “мы решили эту проблему при помощи обучения с подкреплением”, мы не сообщаем никакой информации. Данная группа весьма обширна и в данной статье мы познакомимся с самым популярным методом — Q-learning. Идея та же самая, жестоко бить током нашу нейронную сеть, когда та косячит и одаривать всеми благами мира, когда делает то, что нам нужно. Давайте рассмотрим детали.

Семейство методов обучения с подкреплением

Вообще, пусть меня поправят эксперты, Q-learning может не иметь ничего общего с нейронными сетями. Вся цель этого алгоритма — максимизировать значение Q (вознаграждение, полученное за проход от начального состояния до конечного), используя конечные автоматы.

Мы имеем некоторое кол-во состояний (s1, s2 . ), наш агент может находится в одном из этих состояний в каждый момент времени. Цель агента достичь финального состояния.

Пример конечного автомата

Что остается — это заполнить таблицу переходами на следующие состояния. И найти хитрый способ (алгоритм) как мы можем оптимизировать перемещения по таблице, чтобы заканчивать игру в финальном состоянии всегда с максимальным вознаграждением.

Видео:Принцип оптимальности БеллманаСкачать

Метод динамического программирования Р. Беллмана. Принцип оптимальности

Рассмотрим управляемую систему описываемую следующей системой скалярных дифференциальных уравнений:

(7.4)

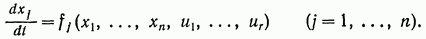
Здесь — фазовые координаты системы, — управляющие силы.

(7.5)

можно заменить систему скалярных дифференциальных уравнений (4) следующим векторным дифференциальным уравнением:

(7.6)

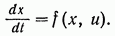
Полагая, что на управляющие силы наложены некоторые ограничения, потребуем при выборе этих сил выполнения условия

(7.7)

где — некоторая область в пространстве , определяемая видом наложенных ограничений.

Пусть целью управления является минимизация функционала

(7.8)

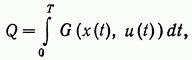
где G — некоторая ограниченная скалярная функция переменных 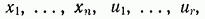, а Т — заданная фиксированная величина.

Метод динамического программирования основывается на сформулированном Р. Беллманом [8] принципе оптимальности. Этот принцип имеет место для систем, последующее движение которых полностью определяется состоянием этих систем в любой текущий момент времени. К таким системам относятся, например, системы, описываемые дифференциальными уравнениями (4), где под состоянием подразумевается положение системы в фазовом пространстве, системы, описываемые уравнениями в конечных разностях с дискретным аргументом и др. Принцип оптимальности сформулирован Беллманом так:

Оптимальное поведение обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения.

Указанная формулировка принципа оптимальности (названного Беллманом интуитивным) относится к системам весьма общего вида. Для управляемых систем, описываемых дифференциальными уравнениями (4), под «поведением» системы следует понимать движение этих систем, а термин «решение» относится к выбору закона изменения во времени управляющих сил.

Для систем, описываемых дифференциальными уравнениями (4), принцип оптимальности совпадает с хорошо известным фактом, что часть экстремали является снова экстремалью.

В качестве примера [85] на рис. 12 показана проходящая через заданную точку оптимальная траектория системы (4), то есть траектория, минимизирующая при условии (7) функционал (8), в котором значение Т предполагается фиксированным. Значение предполагается здесь заранее неизвестным. Точка разбивает рассматриваемую траекторию на два участка 1 и 2. Участку 2 соответствует функционал

(7.9)

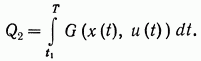
Участок 2 может рассматриваться и как самостоятельная траектория. Эта траектория будет оптимальной, если она доставляет минимум функционалу (9).

Принцип оптимальности утверждает, что участок 2 оптимальной траектории 1—2 сам по себе является оптимальной траекторией системы (4), состояние которой при 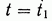есть .

Если допустить противное, то существует (рис. 12) другая траектория доставляющая функционалу (9) значение меньшее, чем доставляет траектория 2. Но тогда на интервале времени оптимальной будет не траектория 1—2, а траектория 1— . Мы пришли к противоречию с исходными данными о том, что траектория 1—2 является оптимальной. Полученное противоречие и доказывает, что участок 2 оптимальной траектории 1—2 является в свою очередь оптимальной траекторией системы (4) на интервале времени .

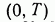
Заметим теперь, что утверждения принципа оптимальности относятся к последующему за данным состоянием движению системы. Для предшествующего данному состоянию движения системы они, вообще говоря, могут не иметь места.

Так, например, если задано лишь начальное состояние системы , то участок 1 оптимальной траектории 1—2 может сам по себе и не быть оптимальной траекторией, то есть может и не доставлять минимума функционалу

(7.10)

Только в том случае, когда задана конечная точка участка 1, этот участок сам по себе также будет оптимальной траекторией.

Таким образом, для управляемых систем принцип оптимальности утверждает, что выбор оптимального управления определяется лишь состоянием системы в текущий момент времени.

Это утверждение дает возможность получения приведенных ниже функциональных уравнений, определяющих закон изменения управляющих сил в задаче об оптимальном управлении.

Видео:Олегу Тинькову запрещён вход на Мехмат МГУСкачать

Усиление обучения: Марков-процесс принятия решений (часть 2)

Дата публикации Aug 30, 2019

Эта история в продолжение предыдущего,Усиление обучения: Марков-процесс принятия решений (часть 1)история, в которой мы говорили о том, как определять MDP для данной среды. Мы также говорили о уравнении Беллмана, а также о том, как найти функцию Value и функцию Policy для состояния.В этой историимы собираемся сделать шагГлубжеи узнать оУравнение ожиданий Беллманакак мы находимоптимальное значениеа такжеОптимальная функция политикидля данного состояния, а затем мы определимУравнение оптимальности Беллмана,

Давайте кратко рассмотрим эту историю:

Уравнение ожиданий Беллмана
Оптимальная политика
Уравнение Беллмана для функции состояния
Уравнение оптимальности Беллмана для функции значения состояния-действия

Так что, как всегда, берите свой кофе и не останавливайтесь, пока вы не гордитесь ».

Давайте начнем с,Что такое уравнение ожидания Беллмана?

Видео:Алгоритм Форда-Беллмана и SPFAСкачать

Уравнение ожиданий Беллмана

Быстрый обзорУравнение Беллманамы говорили в предыдущей истории:

Из вышесказанногоуравнениемы можем видеть, что значение состояния может бытьразложившийсяв немедленное вознаграждение (R [T + 1])плюсзначение государства-преемника (v [S (t + 1)]) с учетом скидки (γ). Это все еще означает уравнение ожиданий Беллмана. Но теперь то, что мы делаем, мы находим ценность определенного государстваподвергаетсяк какой-то политике (π). В этом разница между уравнением Беллмана и уравнением ожиданий Беллмана.

Математически мы можем определить уравнение ожиданий Беллмана как:

Давайте назовем это уравнение 1. Вышеупомянутое уравнение говорит нам, что ценность определенного состояния определяется немедленным вознаграждением плюс значение состояний-преемников, когда мы следуем определенной политике (π),

Точно так же мы можем выразить нашу функцию Value-action-состояния (Q-Function) следующим образом:

Давайте назовем это уравнение 2. Из приведенного выше уравнения мы можем видеть, что значение состояния-действия состояния может быть разложено нанемедленная наградамы выполняем определенное действие в состоянии (s) и переезд в другое состояние (s’) плюс дисконтированная стоимость состояния-действия государства (s’)в отношениинекоторые действия ( ) наш агент возьмет из этого штата подопечных.

Идем глубже в уравнение ожиданий Беллмана:

Во-первых, давайте разберемся с уравнением ожидания Беллмана для функции состояния-состояния с помощью резервной диаграммы:

Эта резервная диаграмма описывает значение нахождения в определенном состоянии. Из состояния s есть некоторая вероятность того, что мы предпримем оба действия. Для каждого действия существует Q-значение (функция значения действия состояния). Мы усредняем Q-значения, которые говорят нам, насколько хорошо быть в определенном состоянии. В основном, это определяет Vπ (s). [Смотрите уравнение 1]

Математически мы можем определить это следующим образом:

Это уравнение также говорит нам о связи между функцией State-Value и функцией Value-Action Value.

Теперь давайте посмотрим на схему резервного копирования для функции значения состояния-действия:

Эта резервная диаграмма говорит, что предположим, что мы начнем с некоторых действий (а). Таким образом, из-за действия (а) агент может попасть в любое из этих состояний окружающей средой. Поэтому мы задаем вопрос,Насколько хорошо действовать (а)?

Мы снова усредняем значения состояний обоих состояний, добавленные с немедленной наградой, которая говорит нам, насколько хорошо выполнить определенное действие (а). Это определяет наш qπ (S, A).

Математически мы можем определить это следующим образом:

где P — вероятность перехода.

Теперь давайте соединим эти резервные диаграммы вместе, чтобы определить функцию состояния-значения, VП (с):

Из приведенной выше диаграммы, если наш агент в какой-тосостояния)и из этого состояния предположим, что наш агент может предпринять два действия, в зависимости от того, какая среда может перевести нашего агента в любую изсостояния (s’), Обратите внимание, что вероятность действий, которые наш агент может предпринять из штатаsвзвешивается нашей политикой и после принятия этого действия вероятность того, что мы приземлимся в любом из государств (s’) взвешивается окружающей средой

Теперь мы задаемся вопросом: насколько хорошо быть в состоянии (ях) после того, как вы предприняли какие-то действия и приземлились в другом (ых) государстве (ах) и следовали нашей политике (π) после того?

Это похоже на то, что мы делали раньше, мы собираемся усреднить значение преемников (s’) с некоторой вероятностью перехода (P), взвешенной с нашей политикой.

Математически мы можем определить это следующим образом:

Теперь, давайте сделаем то же самое для функции значения состояния действия, qπ (S, а):

Это очень похоже на то, что мы сделали вФункция значения состоянияи только она обратная, так что эта диаграмма в основном говорит о том, что наш агент предпринял какие-то действия ( ) из-за которого окружающая среда может посадить нас в любом из государств (s), то из этого состояния мы можем выбрать любые действия (а») взвешены с вероятностью нашей политики (π). Опять же, мы усредняем их вместе, и это дает нам понять, насколько хорошо предпринимать определенные действия в соответствии с определенной политикой (π) все это время.

Математически это можно выразить как:

Итак, вот как мы можем сформулировать уравнение ожиданий Беллмана для данного MDP, чтобы найти его функцию значения состояния и функцию значения состояния.Но это не говорит нам лучший способ вести себя в MDP, Для этого давайте поговорим о том, что подразумевается подОптимальное значениеа такжеОптимальная функция политики,

Видео:Динамическое программированиеСкачать

Функция оптимального значения

Определение оптимальной функции состояния-значения

В среде MDP существует много различных функций-значений в соответствии с различными политиками.Функция оптимального значения — это та, которая дает максимальное значение по сравнению со всеми другими функциями значения., Когда мы говорим, что решаем MDP, это фактически означает, что мы находим функцию оптимального значения.

Итак, математически оптимальная функция состояния-значения может быть выражена как:

В приведенной выше формуле v ∗ (s) говорит нам, какое максимальное вознаграждение мы можем получить от системы.

Определение функции оптимального значения состояния-действия (Q-функция)

По аналогии,Функция оптимального значения состояния-действияговорит нам максимальное вознаграждение, которое мы собираемся получить, если мы находимся в состоянии s и предпринимаем соответствующие действия.

Математически, это может быть определено как:

Оптимальная функция состояния-значения: Это функция максимального значения для всех политик.

Функция оптимального значения состояния-действия: Это функция максимального значения действия для всех политик.

Теперь давайте посмотрим, что подразумевается под Оптимальной политикой?

Видео:СПбГУ -- 2022.04.15 -- Марковские процессы принятия решений: уравнения БеллманаСкачать

Оптимальная политика

Прежде чем мы определим оптимальную политику, давайте знать,что подразумевается под одной политикой лучше, чем с другой политикой?

Мы знаем, что для любого MDP существует политика (π)лучше любой другой политики (π»). Но как?

Мы говорим, что одна политика (π)лучше другой политики (π») если значение функции с политикойπдля всех состояний больше значения функции с политикойπ»для всех государств. Интуитивно это можно выразить как:

Теперь давайте определимсяОптимальная политика:

Оптимальная политикаэто тот, который приводит к функции оптимального значения.

Обратите внимание, что в MDP может быть более одной оптимальной политики. Но,все оптимальные политики достигают одной и той же функции оптимального значения и функции значения оптимального состояния-действия (Q-функция),

Теперь возникает вопрос, как мы находим оптимальную политику.

Нахождение оптимальной политики:

Мы находим оптимальную политику путем максимизацииQ*(s, a), т.е. наша оптимальная функция значения состояния-действия. Мы решаем q * (s, a) и затем выбираем действие, которое дает нам наиболее оптимальную функцию значения состояния-действия (q * (s, a)).

Вышеприведенное утверждение может быть выражено как:

Это говорит о том, что для состояния s мы выбираем действие a с вероятностью 1, если оно дает нам максимум q * (s, a). Таким образом, если мы знаем q * (s, a), мы можем получить из него оптимальную политику.

Давайте разберемся с этим на примере:

В этом примере красные дуги являютсяоптимальная политикаэто означает, что если наш агент пойдет по этому пути, он будетприносить максимальное вознаграждениеиз этого МДП. Кроме того, увидевд *значения для каждого состояния мы можем сказать действия нашего агента, которые принесут максимальное вознаграждение. Таким образом, оптимальная политика всегда действует с более высоким значением q * (функция значения состояния-действия). Например, в состоянии со значением 8 есть q * со значениями 0 и 8. Наш агент выбирает тот, у которого большед *значение то есть 8.

Теперь возникает вопрос,Как мы находим эти значения q * (s, a)?

Именно здесь в игру вступает уравнение оптимальности Беллмана.

Видео:BP2-3-3-08 Алгоритм Форда-БеллманаСкачать

Уравнение оптимальности Беллмана

Функция оптимального значения рекурсивно связана с уравнением оптимальности Беллмана

Уравнение оптимальности Беллмана такое же, как и уравнение ожиданий Беллмана, но единственное отличие состоит в том, что вместо того, чтобы брать среднее значение действий, которые может выполнить наш агент, мы выполняем действие с максимальным значением.

Давайте разберемся с помощью диаграммы резервного копирования:

Предположим, наш агент находится в состоянии S, и из этого состояния он может выполнить два действия (a). Итак, мы смотрим на значения действий для каждого из действий иВ отличие от, Уравнение ожиданий Беллмана,вместоприниматьсреднийнаш агент принимает меры сбольшее значение q *, Это дает нам ценность быть в состоянии S.

Математически это можно выразить как:

Аналогично, давайте определим уравнение оптимальности Беллмана дляФункция значения состояния состояния (Q-функция),

Давайте посмотрим на схему резервного копирования для функции значения состояния-действия (Q-функция):

Предположим, наш агент совершил действие a в каком-то состоянии s. Теперь, на окружающей среде, что это может взорвать нас в любое из этих государств (s’). Мы по-прежнему берем среднее значение обоих государств, но единственноеразницанаходится в уравнении оптимальности Беллмана мы знаемоптимальные значениякаждого из состояний. В отличие от уравнения ожиданий Беллмана, мы просто знали значение состояний.

Математически это можно выразить как:

Давайте снова сшиваем эти резервные диаграммы для функции состояния-значения:

Предположим, наш агент находится в состоянии s, и из этого состояния он предпринял какое-то действие (a), когда вероятность совершения этого действиявзвешенныйполитикой. И из-за действия (а), агент может быть взорван в любом из состояний (s’) где вероятность взвешена окружающей средой.Чтобы найти значение состояния S, мы просто усредняем оптимальные значения состояний (s ’)., Это дает нам ценность пребывания в состоянии S.

Математически это можно выразить как:

Максимум в уравнении потому, что мы максимизируем действия, которые агент может предпринять в верхних дугах. Это уравнение также показывает, как мы можем связать функцию V * с самим собой.

Теперь давайте посмотрим на уравнение оптимальности Беллмана для функции значения состояния-действия, q * (s, a):

Предположим, наш агент был в состоянииsи потребовалось какое-то действие ( ). Из-за этого действия окружающая среда может высадить нашего агента в любой из штатов (s’) и из этих состояний мы получаемразворачиваниядействие, которое предпримет наш агент, то есть выбор действия смаксимальное значение q *, Мы поддерживаем это до самого верха, и это говорит нам о значении действия a.

Математически это можно выразить как:

Давайте посмотрим на пример, чтобы понять его лучше:

Посмотрите на красные стрелки, предположим, что мы хотим найтиценностьсостояния со значением 6 (в красном), как мы видим, мы получаем вознаграждение -1, если наш агент выбирает Facebook, и вознаграждение -2, если наш агент хочет учиться. Чтобы найти значение состояния в красном, мы будем использоватьУравнение Беллмана для функции состояниято естьучитывая, что два других состояния имеют оптимальное значение, мы возьмем среднее значение и максимизируем оба действия (выберите то, которое дает максимальное значение), Таким образом, из диаграммы мы можем видеть, что переход на Facebook дает значение 5 для нашего красного состояния, а при обучении — значение 6, а затем мы максимизируем два, что дает нам 6 в качестве ответа.

Теперь, как мы решаем уравнение оптимальности Беллмана для больших MDP. Для этого мы используемАлгоритмы динамического программированиянравитсяИтерация политикиЗначение итерации, которую мы рассмотрим в следующем рассказе и другие методы, такие какQ-Learningа такжеSarsaкоторые используются для изучения временных различий, о которых мы расскажем в будущем.

Поздравляю с таким большим успехом! 👍

Надеюсь, что эта история повышает ценность вашего понимания MDP. Хотелось бы связаться с вами на #Instagram,

Спасибо, что поделились со мной своим временем!

Если вам нравится этот, пожалуйста, дайте мне знать, нажав на 👏. Это помогает мне писать больше!