Уравнение бегущей волны с синусом

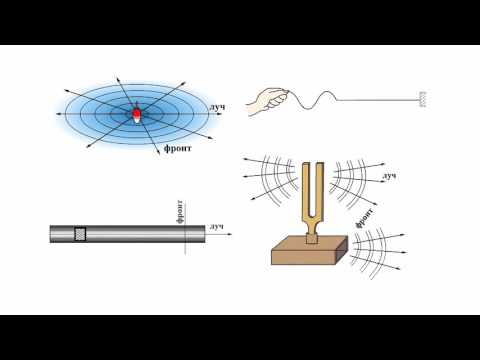
Ось X направим вдоль шнура, а начало отсчета свяжем с левым концом шнура (см. рис. 4.11). Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой S. Для описания волнового процесса необходимо знать значение S в любой точке шнура в любой момент времени, а следовательно, знать вид функции s = s(x, t).

Заставим конец шнура (точка х = 0) соверпгать гармонические колебания с частотой ω. Колебания этой точки будут происходить по закону

если начальную фазу колебаний считать равной нулю. Здесь s_m — амплитуда колебаний (рис. 4.14, а).

Колебания распространяются вдоль шнура (оси X) со скоростью v и в произвольную точку шнура с координатой х придут спустя время

Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. 4.14, б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой s_m, но с другой фазой:

Это и есть уравнение бегущей волны*, распространяющ;ей-ся в положительном направлении оси X. В случае, когда начальная фаза колебаний в точке x = 0 равна не нулю, а произвольной величине φ₀, уравнение бегуньей волны запишется так:

Амплитуда колебаний s_m называется амплитудой волны. Величину, стоящую под знаком синуса, называют фазой волны. В общем случае фаза волны равна:

Разумеется, вместо синуса при записи уравнения бегущей волны мы могли бы использовать и косинус. Замена синуса на косинус эквивалентна изменению начальной фазы на π/2.

Выражение (4,5.5) для фазы волны можно преобразовать, если выразить циклическую частоту колебаний ω через частоту v или период Т, а скорость волны v заменить ее значением согласно формуле (4.3.2). Для случая φ₀ = 0 получим:

Уравнение (4.5.3) бегущей гармонической волны примет при этом форму:

В этой форме записи отчетливо видно, что функция s(x, t) обладает периодичностью двоякого рода. Она периодична по времени при фиксированном х (период равен периоду колебаний Т, см. рис. 4.14) и периодична по пространству при фиксированном моменте времени (период равен длине волны λ, см. рис. 4.11). Это означает, что при замене t ⇒ t + Т или x ⇒ x + λ смещение s от положения равновесия согласно уравнению (4.5.7) остается одним и тем же.

Итак, в бегущей волне все точки среды (участки шнура) совершают вынужденные колебания с одним и тем же периодом, но с различными фазами. Две точки с координатами х₁ и х₂ имеют разность фаз

При x₂ — х₁ = λ, разность фаз равна 2π. Точки колеблются синфазно. Если х₂ — х₁ = λ/2. О колебания происходят в противофазе.

Надо отметить, что строго гармонических волн не существует. Из-за неизбежных потерь механической энергии амплитуда колебаний постепенно уменьшается по мере распространения волны от источника возбуждения колебаний. Можно приближенно говорить о гармонической волне в том случае, когда затухание бегущей волны на одной длине волны очень мало и по всей длине шнура укладывается много длин волн. Уравнение (4.5.3) описывает процессы не только в поперечной волне, но и в продольной, например в длинном упругом стержне. При этом s(x, t) по-прежнему имеет смысл смещения колеблющихся частей стержня от положения равновесия. Эти смещения в продольной волне происходят вдоль направления распространения волны (оси X).

* Волна называется бегущей по той причине, что, как мы увидим в следующем параграфе, существуют и стоячие волны, у которых максимумы и минимумы колебаний не перемещаются с течением времени.

Видео:Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Бегущая волна

Содержание:

Бегущая волна — волновое движение, при котором поверхность равных фаз (фазовые волновые фронты) перемещается с конечной скоростью (постоянной для однородной среды). Примерами могут служить упругие волны в стержне, столбе газа или жидкости, электромагнитная волна вдоль длинной линии или в волноводе.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Видео:Механические модели волн. 1.Скачать

Бегущие волны

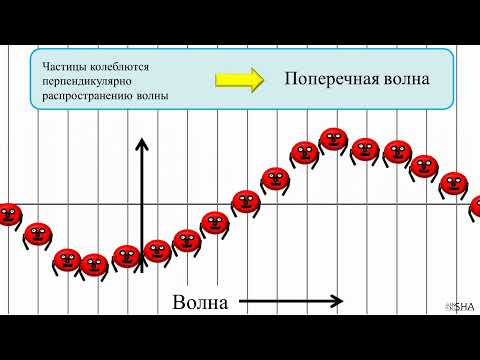
Бегущими называются волны, которые распространяются в пространстве или среде. У механических волн частицы вдоль направления распространения волны перемещаются на максимальное расстояние от точки равновесия при прохождении через нее гребня или впадины волны. Частицы, разделенные целым числом длины волны, колеблются в одной фазе друг с другом.

Распространение деформации

Каждое тело обладает в той или иной степени упругостью, т. е. способностью восстанавливать свою форму, искаженную в результате кратковременного действия силы. Эта способность тела является причиной того, что всякое механическое действие передается телом с конечной скоростью. Если бы существовал абсолютно твердый, неспособный деформироваться стержень, то он мог бы двигаться только как целое, действие силы распространялось бы по такому телу мгновенно. Абсолютно пластическое тело, деформирующееся без малейшего восстановления формы, было бы неспособно к какой бы то ни было передаче механического действия.

В упругом теле деформация передается последовательно от одной точки тела к соседней. Если стержню нанесен сжимающий удар молотком, то на конце стержня образуется уплотнение, которое распространится с определенной скоростью с вдоль тела. Если в твердом теле создан местный кратковременный изгиб, то он также будет передаваться с конечной скоростью по твердому телу. То же самое справедливо для любой деформации. Пробегающие по телу при разных механических действиях деформации обычно демонстрируют при помощи пружин (рис. 56)

Упругостью сжатия и растяжения обладают как твердые тела, так и жидкие и газообразные. Поэтому в любых телах возможна передача этих деформаций. Что же касается деформаций сдвига, кручения, изгиба, то такие деформации могут передаваться только твердыми телами, обладающими соответствующей упругостью. При деформации сжатия и растяжения движения частиц происходят, в том же направлении, в котором передается механическое действие. В подобных случаях мы говорим о продольном распространении деформации. При сдвиге, изгибе, кручении направление движения частиц может образовать, вообще говоря, произвольный угол с направлением, по которому передается энергия.

Всегда возможно выделить направление, в котором передается механическое действие, а затем разложить смещение частицы тела по трем взаимно перпендикулярным осям, одна из которых лежит вдоль линии распространения, а две других — в перпендикулярной плоскости. Поэтому в наиболее сложном случае можно рассматривать распространяющуюся деформацию как совокупность трех движений: двух поперечных и одного продольного.

Скорость распространения упругой деформации зависит от механических свойств тела; ее, как показывает теоретическая физика, можно связать с другими физическими константами тела. Так, для продольных волн скорость распространения выражается простой формулой:

Здесь — плотность тела, а х — сжимаемость. Большая плотность тела приводит к увеличению инертности частиц тела и, следовательно, уменьшает скорость распространения упругих волн. Малые сжимаемости говорят о том, что даже малым деформациям соответствуют большие упругие силы. Это обстоятельство приводит к увеличению скорости распространения деформации.

В таком виде этой формулой пользуются обычно для жидкостей. Так, например, вода при изменении давления на 1 атм сжимается на своего объема. Значит, сжимаемость, равная (см. стр. 138) по определениюПлотность

воды Отсюда для скорости распространения деформации в воде получим

Для газов формулу скорости целесообразно преобразовать. Так как процесс передачи уплотнения в газе весьма быстр, то сжатия и разрежения газа можно считать адиабатическими, т. е. происходящими без теплообмена. Ниже (стр. 150) будет получено уравнение адиабатического процесса, из которого легко вывести связь коэффициента сжимаемости с давлением газа: Тогда Для идеального газа плотность —масса моля газа, a — его объем) будет пропорциональна дроби (так как т. е.» скорость распространения деформации в газе

Здесь — коэффициент, значение которого легко вычисляется при помощи уравнений, рассматриваемых позднее (стр. 149).

Таким образом, скорость распространения деформации в газе, в том числе и скорость распространения звуковых волн, о которых речь пойдет дальше, пропорциональна корню квадратному из температуры и не зависит от давления газа. Интересна зависимость от молекулярного веса: скорость распространения деформации в водороде равна 1263 м/с, в то время как в воздухе мы имеем хорошо знакомое число 331 м/с.

Для продольных волн, распространяющихся в твердом теле, заменяют обычно коэффициент сжимаемости на модуль упругости. Так как по определению модуль упругости

то очевидно, что при отсутствии поперечных движений поскольку линейное относительное сжатие будет равно объемному. Формула скорости запишется в виде

Насколько хорошо она выполняется, можно судить по следующим примерным числам:

Проверку этой формулы надо проводить, изучая скорость распространения звука в тонких стержнях. Дело в том, что более глубокое рассмотрение вопроса показывает, что формула должна быть справедлива только для таких тел. Для тел иной формы, а также для распространения звука в сплошной среде теория приводит к другим выражениям, которые мы приводить не будем.

Следует также заметить, что таблица приведенных величин может служить лишь для ориентировки. Скорости звука в разных сортах стекол, разных сортах дерева, стали и т. д. могут существенно различаться.

Возникновение волнового движения

Многочисленными способами можно подвести к отдельной точке тела или среды непрекращающиеся колебания. Периодически действующая в какой-либо точке тела сила создаст периодически меняющуюся деформацию, которая будет передаваться от точки к точке тела с определенной скоростью. В колебательное движение придут все точки тела. При этом из-за конечности скорости распространения деформации точки тела будут приходить в колебание одна за другой. Если тело безгранично, то такое колебание будет все время продвигаться вперед, образуя бегущую волну.

Хотя безграничных тел и не существует, но длина большого тела не скажется на характере явлений по той причине, что колебания не дойдут до его конца из-за неизбежных потерь энергии.

Рассмотрим волну, бегущую в практически неограниченном теле вдоль какого-нибудь направления.

Пусть точка, находящаяся в начале отсчета, колеблется согласно уравнению Запишем уравнение колебания точки, расположенной вдоль линии распространения деформации на расстояниях от начальной. Мы не можем записать его в том же виде, так как эта точка пришла в колебание с запозданием на время нужное для распространения деформации на расстояние х. Поэтому колебание точки х должно быть сдвинуто по фазе по отношению к начальной точке. Точка х будет находиться в момент времени в той же фазе колебания, в какой находилась начальная точка в момент времени, на более ранний. Следовательно, уравнение колебания точки, сдвинутой на расстояние х от начала координат, имеет вид

где — сдвиг фазы.

Написанное уравнение называют уравнением волны, оно охватывает колебания всех точек, расположенных на любых расстояниях по отношению к начальной.

Положим, что источник волны далек от наблюдателя и фронт волны давно ушел вперед. Мы рассматриваем участок линии вдоль оси х, охваченный волновым движением. На первый взгляд может показаться, что введение нового термина не оправдано. Все точки

участка будут колебаться, это ясно. Но увидим ли мыдвижение волны, сможем ли сказать, двигается она вправо или влево? Внимательное рассмотрение показывает, что специфичность волнового движения легко обнаружить. Если волна движется слева направо, то правая соседняя точка будет запаздывать по фазе по сравнению с левой. В обратном случае она будет опережать ее. Волны, бегущие влево и вправо, показаны на рис. 57. Каждая синусоида — это мгновенный снимок волны. В каждое следующее мгновение эта синусоида, как жесткое целое, перемещается в том направлении, куда передается энергия.

Отсюда понятно, как отражается направление волны на виде уравнения волны. Если волна движется вдоль оси координат, то значение координаты х будет входить со знаком минус. При движении волны против направления отсчета координаты в аргументе косинуса надо изменить знак на обратный:

Запишем уравнение мгновенного снимка волны для какого-либо времени, равного кратному числу периодов:

Знак минус можно отбросить, так как косинус— четная функция. Из вида уравнения сразу же следует, что период этой синусоиды равен

Этот пространственный период, т. е. расстояние, через которое повторяется волнообразное распределение, носит название длины волны. Мы получили известное соотношение, связывающее скорость движения волны с длиной волны и периодом колебания точки.

При волновой передаче деформации через тело по закону синуса меняется ряд физических величин: смещение точки от положения равновесия, скорость колеблющихся частиц, давление и плотность. Поэтому выражение волны, которым мы оперируем, является весьма общим. Под величиной можно понимать любую из перечисленных физических величин, изменяющихся по закону синуса при движении волны вдоль направления х. Правда, следует отметить, что волны давления, скорости, смещения не обязаны быть в одной фазе. Например, ясно, что волна скоростей колеблющихся частиц будет сдвинута по фазе на 90° по отношению к волне смещений. Ведь скорость точки максимальна, когда она проходит положение равновесия.

Волны давления и скорости колебания

Представляет интерес соотношение между амплитудами волн различных физических величин. Остановимся на этом вопросе лишь для случая продольных волн, распространяющихся в газе. Нас могут заинтересовать волны смещения, скоростей частиц, избыточного давления. Так как теория возникла для волн, воспринимаемых слухом, то избыточное давление часто называют звуковым давлением и, отбрасывая значок обозначают через

Если амплитуда волны смещения А, то амплитуда волны скоростей По фазе эти две волны сдвинуты на 90°.

Выясним теперь связь между амплитудой скорости колебания и амплитудой давления. Сопоставив общее определение с его выражением для газов (стр. 97), получим для звукового давления формулу

где Р — давление газа, или, используя соотношение

Вполне естественно, что имеется прямая связь между избыточным давлением и относительным сжатием в том же месте газа.

Но величину относительного сжатия объема можно связать с амплитудой смещения колеблющихся частиц. Отметим вдоль линии распространения две точки: В продольной волне изменение плотности происходит лишь благодаря смещениям в направлении распространения. Выделим мысленно в тазе объем, ограниченный сечениями Когда идет волна, молекулы, находящиеся внутри этого объема,сместятся.Следить нам нужно только за граничными сечениями. Если молекулы слоя сместятся на а молекулы слоя то линейный размер объема изменится от значения в отсутствие волны на величину Относительное изменение длины, а значит, и объема будет Переходя к пределу, чтобы получить величину, характерную для точки пространства, получима для давления

Этим доказано, что давление изменяется в фазе со скоростью колебания частиц в волне. есть амплитуда скорости колебания. Таким образом, амплитуда давления выражается через амплитуду скорости следующим образом:

В акустике и измеряют обычно в см/с, а давление — в Для воздуха при комнатной температуре для этих единиц Величина называется акустическим, или волновым, сопротивлением. Смысл названия, очевидно, такой: чем больше сопротивление, тем меньше скорость колебания частиц при тех же величинах избыточного давления.

Подсчитаем акустические сопротивления некоторых материалов:

Поток энергии

Волновое движение переносит энергию из одного места пространства в другое. Однако следует помнить, что все точки среды, участвующие в передаче энергии, все время колеблются около положения неизменного равновесия.

Все точки тела участвуют в колебании. Поэтому единица объема обладает колебательной энергией, равной

где — плотность, т. е. масса единицы объема, а — амплитудное значение скорости колебания. Используя для последней величины знакомое нам выражениегде А — амплитуда смещения, а — частота, можно записать плотность колебательной энергии тела в виде

Эта энергия распространяется со скоростью Мы вправе поставить перед собой следующий вопрос: чему равна интенсивность волны, т. е. количество энергии, проходящее в единицу времени через единицу площади, перпендикулярную к направлению распространения волны? Вместо того чтобы говорить об интенсивности волны, довольно часто говорят о потоке колебательной энергии, понимая под этим энергию, проходящую в единицу времени (мощность) через данную площадь. Рассуждение ничем не отличается от такового для случая воды, текущей по трубе. Через единицу времени волна проходит путь и приносит энергию в объем цилиндра с длиной с и площадью, равной единице. Так как на единицу объема приходится энергия то на этот объем придется энергия.Это и есть значение интенсивности волны:

Мы видим, что интенсивность волны имеет смысл потока энергии, проходящего через единицу площади. Это было впервые указано Н. А. Умовым, разработавшим теорию движения энергии в телах.

До сих пор предполагалось, что волновое движение распространяется вдоль прямой линии. Подобное рассмотрение имеет цену для изучения деформации, бегущей вдоль стержней, струн, воздушных столбов и пр. Однако нас интересуют и такие случаи, когда волновым движением захвачена область трехмерного пространства.

Для описания трехмерной волны нужно знать, как движется ее фронт. Чтобы отыскать фронт волны, надо суметь для данного мгновения отметить все точки пространства, находящиеся в одинаковых фазах колебания. Отмечая последовательное положение этой поверхности равных фаз, т. е. фронта волны, мы получим ясное представление о характере волнового движения

Поверхность волны, вообще говоря, может иметь любую форму. Какой же смысл тогда получит направление распространения волны? За это направление естественно принять нормаль к фронту волны.

Если среда вполне однородна и волна излучается в какой-либо точке среды, то фронт ее будет сферическим. Такая волна распространяется по радиусам от центра. На больших расстояниях от центра излучения уже значительные участки фронта волны будут с точностью опыта казаться плоскими. Так возникает представление о плоской волне, распространяющейся в направлении нормали к фронту. Если излучатель волны имеет вид линии, то возникнет цилиндрическая волна, распространяющаяся по радиусам цилиндра. Разные типы волн показаны на рис. 58.

Если оставить без внимания всякого рода потери энергии, происходящие при движении плоской волны, то можно утверждать необходимость равенства количества энергии, проходящей через последовательные положения поверхностей равной фазы. Поэтому интенсивность плоской волны не будет меняться в процессе ее распространения. Однако иначе обстоит дело для сферических и цилиндрических волн. Так как поверхности равной фазы увеличиваются по своей площади пропорционально квадрату расстояния степени расстояния соответственно для сферических и цилиндрических волн, то интенсивности этих волн должны меняться обратно пропорционально квадрату расстояния для сферической волны и первой степени расстояния для цилиндрической волны. Только в этом случае будет соблюден закон сохранения энергии.

Интенсивность волны пропорциональна плотности колебательной энергии, которая пропорциональна квадрату амплитуды колебания. Отсюда следует: амплитуда сферической волны обратно пропорциональна первой степени расстояния от излучающего центра, а амплитуда цилиндрической волны обратно пропорциональна корню квадратному из расстояния от излучающеи линии: для сферической волны,для цилиндрической волны. Здесь расстояниетак же как и ранее откладывается вдоль направления распространения волны.

Пусть под водой помещен источник колебаний с частотой 1 кГц, создающий поток энергии Оценим амплитуду смещения А молекул воды, их ускорение В и амплитуду колебательной скорости Из формул предыдущих параграфов следует, что

Для воды

Если такой же поток энергии при прежней частоте колебаний создается в воздухе, для которого то

Затухание упругих волн

Реальные волны, распространяющиеся в среде (твердой, жидкой или газообразной), уменьшают свою интенсивность значительно быстрее, чем по закону обратных квадратов. Сказываются потери механической энергии, превращение ее в тепло.

Закон падения интенсивности какого-либо излучения при прохождении через среду почти всегда (для любой среды и любого излучения) может быть получен из следующего рассуждения. Если волна прошла слой толщины то потерянная интенсивность должна быть во всяком случае пропорциональна падающей интенсивности и толщине слоя, т. е.

Это уравнение можно проинтегрировать; полагая интенсивность равной в точке и равной в точке х, получим закон, справедливый для конечных расстояний:

Таким образом, интенсивность волны падает по экспоненциальному закону.

В акустике принято говорить о затухании амплитуды колебания. Поскольку интенсивность пропорциональна квадрату амплитуды, то затухание амплитуды колебания будет выражаться тем же законом, только коэффициент затухания (или поглощения) будет в два раза меньшим:

Укажем на смысл коэффициента поглощения Измеренный в обратных сантиметрах (в показателе должна стоять безразмерная величина), он дает величину, обратную толщине, на протяжении которой интенсивность или амплитуда излучения ослабляются в раз.

Формулировка закона экспоненциального затухания, разумеется, лишь частично решает проблему поглощения упругой волны средой. Более важными являются поиски зависимости коэффициента поглощения от свойств среды и от частоты излучения.

Для многих веществ найдено, что затухание упругой волны (основные данные относятся к звуковым волнам в воздухе) возрастает с частотой колебания. А именно* коэффициент поглощения

Для воздуха Таким образом, на протяжении 1 км плоская волна частоты 100 Гц ослабляется в

1,015, а очень высокий звук частоты 20 ООО Гц — в раз! Ультразвуковые колебания затухают столь быстро, что их передача на расстояния, большие нескольких сотен метров, совершенно нереальна.

Однако монотонный ход поглощения с частотой может нарушаться. Некоторые вещества обладают избирательным поглощением звука в относительно узкой области частот. Так, например, поглощение ультразвука углекислым газом имеет пик при частотах около 277 кГц. Если провести плавную параболу в соответствии с формулой для коэффициента поглощения, то она будет хорошо совпадать с экспериментальными данными во всех областях, кроме указанной. При частотах же около 277 кГц, поглощение будет примерно в 20 раз больше, чем это следует из параболического закона.

Что касается зависимости коэффициента поглощения от свойств среды, то здесь для продольных волн в газах и жидкостях имеет место следующая закономерность. Коэффициент поглощения обратно пропорционален кубу скорости упругой волны и прямо пропорционален кинематической вязкости. Столь резкая зависимость от скорости распространения, а также значительная величина кинематической вязкости воздуха приводят к тому, что поглощение звуковых и ультразвуковых волн в жидкости примерно в 1000 раз меньше, чем в воздухе; это значит, что при той же самой частоте упругие волны будут распространяться в воде на расстояния в тысячу раз большие, чем в воздухе.

Поглощение поперечных волн в твердых телах также сильно зависит от свойств тела; так, поглощение в резине, пробке и стекле соответственно в 13 ООО, 8500 и 130 раз больше, чем в алюминии.

Мы не останавливаемся на теориях поглощения упругих волн в телах ввиду их сложности.

Интерференция волн

Если имеется не один, а несколько источников волн, то каждая точка среды примет одновременно участие в нескольких волновых движениях. Оказывается всегда возможным рассматривать колебание физической величины, происходящее благодаря действию нескольких волн, как сумму колебаний, каждое из которых имело бы место, если бы действовала одна волна.

Положим, что из двух точек, расположенных на некотором расстоянии друг от друга, исходят шаровые волны. При помощи уравнения волны можно найти значение амплитуды колебания в любой момент времени для любой соседней точки. Если интересующее нас место находится на расстоянииот первого и от второго источника волн, то колебания в нем представятся формулой

Результатом сложения двух колебаний, отличающихся только фазами, является, как нам известно, также гармоническое колебание, совершающееся с амплитудой зависящей от разности фаз складывающихся колебаний. Разность фаз равна в этом случае

Итак, вообще говоря, все точки рассматриваемого нами волнового поля будут находиться в колебании. Но амплитуды этих колебаний в разных точках будут разными. Обращают на себя внимание два крайних случая. Во-первых, найдутся такие точки, в которых складывающиеся колебания уничтожат друг друга. Эти точки будут удовлетворять условию

где — разность фаз равняется нечетному числу Напротив, если

разность фаз равна четному числу то амплитуды колебания будут складываться арифметически, т. е. в максимальной степени усиливать друг друга.

Разность называют разностью хода волн; термин не нуждается в пояснениях. Условия максимумов и минимумов амплитуды можно с помощью этого понятия сформулировать несколько иначе. Условие максимума

говорит, что разность хода между волнами, пришедшими в данную точку, должна равняться целому числу длин волн. Условие минимума

говорит, что разность хода должна равняться нечетному числу полуволн. Эти условия имеют весьма наглядный смысл: волны усиливают друг друга, если накладывается горб к горбу, и уничтожаются, если накладывается горб на впадину.

Наложение волн, при котором происходит сложение их амплитуд, называется интерференцией.

Как известно из аналитической геометрии, кривые линии, удовлетворяющие условию постоянства разности расстояний от точки

кривой до двух фокусов, суть гиперболы. Если провести плоское сечение через точечные источники и отметить на рисунке места максимального усиления и места уничтожения волн, то они попадут на гиперболы. Соответствующие кривые показаны на рис. 59. Можно без труда наблюдать такую картину на воде, если заставить интерферировать два источника, посылающих водяные круги из соседних точек.

Таким же точно способом может быть рассмотрена интерференция любого числа источников волн.

Принцип Гюйгенса — Френеля. Отражение и преломление волн

Бросается в глаза полная равноправность всех колеблющихся точек волнового поля. Они различаются только фазами. С этой точки зрения возникает естественная мысль: мы имеем право рассматривать любую точку волнового поля как самостоятельный источник сферических волн.

Справедливость этой идеи, высказанной впервые в 1690 г. Христианом Гюйгенсом, можно проверить, д&тая попытки построения фронта волны по данным о волновом поле на некоторой граничной поверхности. При этом необходимо учитывать, что отдельные (так называемые элементарные) сферические волны будут друг с другом интерферировать. В указании возможности такой процедуры и состоит принцип Гюйгенса, дополненный Френелем.

В чем же значимость этого принципа? Представим себе, что волна надает на непрозрачный экран с несколькими отверстиями. Из принципа Гюйгенса — Френеля следует возможность поисков волнового поля за экраном без всякого знания об источниках полей. Достаточно знать интенсивность поля в плоскости экрана, принять, что из каждой точки экрана распространяется сферическая волна. Амплитуда волны в любом месте пространства найдется сложением (интерференцией) всех элементарных волн, выходящих из отверстий в экране. Откладывая рассмотрение вопросов, связанных с прохождением волн через экраны (эти проблемы представляют наибольший интерес для световых волн), мы остановимся на применении принципа Гюйгенса — Френеля для объяснения явлений отражения и преломления волн.

Рассмотрим участок плоской волны, падающей на границу раздела двух сред. Как известно, волна любого происхождения отражается под углом, равным углу падения. Но почему должно так произойти? На это отвечает принцип Гюйгенса. Все точки границы сред можно рассматривать как источники элементарных волн. Первая элементарная волна отправится от той точки, куда раньше всего придет падающая волна. Далее поочередно будут возбуждаться другие точки границы раздела и, наконец, последней придет в колебание та- точка, которой падающая волна достигает позже всего. На рис. 60 изображены положения элементарных волн для того момента времени, когда падающая волна достигла последней точки.

Элементарные волны создали фронт, образующий с границей раздела тот же угол, что и падающая волна. Действительно, скорости распространения падающей волны и отраженных волн одинаковы, значит, радиус наибольшей сферы должен равняться пути, пройденному падающей волной за время от момента возбуждения первой до момента возбуждения последней точки.
Таким же точно образом без труда строится фронт отраженной сферической волны. Это построение произведено на рис. 61. На рис. 62 приведена фотография отражения стенкой звуковой волны.

Рассмотрим теперь элементарные волны, идущие от границы раздела во вторую среду и образующие фронт преломленной волны (рис. 63). Различные среды отличаются плотностями (и упругими свойствами), а значит, и скоростями распространения волн. В более плотной среде скорость волны меньше. Проделаем такое же построение, что и для отражения, т. е. изобразим на рисунке фронт элементарных волн для того момента времени, когда падающая волна

достигла последней точки. Фронт повернулся из-за различия в скоростях распространения. Если волна попадает в более плотную среду, то радиус наибольшей элементарной волны дач жен быть меньше пути, пройденного падающей волной от момента возбуждения первой точки до момента возбуждения последней точки границы. При этом отношение этих длин должно как раз равняться отношению скоростей распространения волн. С другой стороны, как влдно из рис. 63, отношение указанных расстояний равно отношению синусов углов падения и преломления. Таким образом мы и приходим к известному правилу преломления волн:

Направление распространения приближается к нормали к границе раздела, если волна переходит из менее плотной среды в более плотную, и обратно — при переходе в менее плотную среду волна отклоняется от нормали. Отношение носит название коэффициента преломления.

Коэффициент отражения

Объяснение геометрии отражения и преломления может показаться малоинтересным приложением теории. Однако волновая теория позволяет сделать гораздо большее, а именно, выяснить вопрос о долях отраженных и преломленных волн в зависимости от свойств сред, границу между которыми мы рассматриваем. Мы ограничимся лишь простейшим случаем нормального падения продольной волны на границу двух сред. Этим будут облегчены вычисления. Характер же доказательства одинаков для всех мыслимых случаев.

Следующее положение является исходным для рассуждений этого типа. На границе двух сред ни скорость колебания частиц и, ни избыточное давление не могут меняться скачком. Интуитивно ясно, что иначе и быть не может. Строгим рассмотрением можно показать, что это положение следует из основных законов физики.

С одной стороны границы имеются волны с мгновенными значениями с другой стороны границы имеется волна с мгновенным значением скорости Непрерывность скоростей дает условие: непрерывность давлений: Однако, всматриваясь в написанные два уравнения., мы видим, что они несовместны, так как В чем же дело? ‘Мы забыли, что мгновенные значения скоростей и давлений — векторные величины и даже в простейшем случае, когда векторы смещений лежат в одной плоскости, амплитуды могут различаться знаком. Всматриваясь в написанные уравнения, мы видим, что они становятся совместными лишь в том случае, если принять противоположными знаки амплитуд отраженных волн скорости колебания и давления и записать уравнения непрерывности в виде

Предоставляем читателю убедиться в том, что все другие расстановки знаков оставят уравнения несовместными.

Так как амплитуды — положительные величины, то сумма должна быть больше разности. Поэтому первая пара уравнений справедлива, если а вторая пара имеет место для обратного случая. Первая пара уравнений возникает тогда, когда все амплитудные векторы скорости колебания смотрят в одну сторону, а фаза отраженной волны давления отличается на 180°, т. е. отраженная волна имеет амплитудный вектор, смотрящую в противоположную сторону по отношению к падающей и преломленной волнам. Вторая пара соответствует обратному случаю.

Интересное явление поворота амплитудного вектора при отражении носит название потери полволны или скачка фазы на 180°. Действительно, изменение знака в уравнении волны

где — любая физическая величина, может быть получено внесением в аргумент косинуса сдвига фаз на 180°. С другой стороны, сдвиг на 180° равносилен перемещению волнового распределения на полволны.

Итак, на границе двух сред падающая и отраженная волна либо максимально усиливают друг друга, либо максимально ослабляют.

Запомним, что для волны скоростей колебания потеря полволны при отражении происходит при падении в среду с большим сопротивлением (иногда неточно говорят: в среду с большей плотностью). Волна смещения неразрывно связана с волной скорости колебания и терпит вместе с ней потерю полволны.

Прошедшая во вторую среду волна не терпит скачка фазы.

Из написанных уравнений найдем, совместно решая их, значение коэффициента отражения

также найдем коэффициент преломления т. е.

Для воздуха и твердых тел волновые сопротивления разнятся очень сильно. Для воздуха, как мы указывали, а для стали Это значит, что звук, падающий из воздуха на сталь, практически отражается полностью и почти не проникает в среду. Легко подсчитать, что для границы воздух.— вода

Явление Доплера

До сих пор молчаливо предполагалось, что источник волны и приемник ее (т. е. наблюдатель) оба покоятся по отношению к среде, в которой распространяется волна. Своеобразные эффекты, на которые впервые указал Доплер (1842 г.), наблюдаются в том случае, когда источник или наблюдатель или, тем более, оба вместе движутся по отношению к среде. Они заключаются, прежде всего, в том, что при движении источника волн наблюдатель измерит частоту колебаний при движении наблюдателя он измерит частоту колебаний Эти частоты отличны друг от друга и от той частоты v, которая измеряется при неподвижных наблюдателе и источнике.

При рассмотрении эффекта Доплера надо, прежде всего, обратить внимание на то обстоятельство, что волна, вышедшая от источника, распространяется совершенно независимо от движения источника и наблюдателя. Поэтому при движении относительно среды источник или наблюдатель могут надвигаться или, напротив, убегать от движущейся волны.

Почему же подобные движения могут привести к измерениям частоты, отличным от ее «истинного» значения? Дело в том, что наблюдатель определяет частоту колебаний как число волн, которое приходит в его прибор за единицу времени, в то время как по формуле это число есть число длин волн, укладывающееся ‘на пути, пройденном в единицу времени. Если наблюдатель движется к источнику со скоростью то за 1 с он зарегистрирует подход не V волн, а большего их числа, и притом во столько раз больше, во сколько относительная скорость волны и наблюдателя больше Таким образом,

Если источник движется к приемнику, то наблюдатель опять-таки зафиксирует большее число волн, чем в случае, когда источник и приемник неподвижны. Однако причина увеличения здесь иная.

На первый взгляд это не очевидно. Но дело в том, что движение источника при неизменной частоте колебаний приводит к изменению расстояний между синфазными точками волны. Если первый случай можно грубо интерпретировать как движение наблюдателя навстречу колонне спортсменов, бегущих с одинаковой скоростью и постоянными интервалами между собой, то ясно, что во втором случае схема рассуждения должна быть другой. Теперь можно говорить о медленном смещении линии старта (бегуны через равные промежутки времени прыгают с перемещающегося вдоль трассы автомобиля), что приведет к изменению расстояний между ними. Вместо они станут Если линия старта (источник) смещается по направлению к наблюдателю и за 1 с выпускается V спортсменов, то за 1 с они распределятся на участке Таким образом, интервал между спортсменами (длина волны) Частота, с которой спортсмены, движущиеся со скоростью с, пересекают линию финиша (частота колебаний, воспринимаемая наблюдателем),

Обе полученные формулы одинаково годятся и тогда, когда источник и наблюдатель удаляются друг от друга; в этих случаях надо заменить знак скорости на обратный.

Итак, показано, что при сближении источника и наблюдателя измеряемая частота колебаний, излучаемых источником, возрастает. При удалении частота падает.

Хорошо известный пример эффекта Доплера для звуковых волн дает наблюдение звука гудка приближающегося и удаляющегося поезда. При приближении поезда мы слышим звук с частотой выше истинной. Высота тона меняется скачком, когда поезд проносится мимо наблюдателя. Поезд удаляется, теперь слышимый звук имеет частоту ниже истинной. Если поезд идет со скоростью 70 км/ч, то величина скачка составит

12% от истинной частоты.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Получение уравнения плоской бегущей волны.Скачать

Уравнение бегущей волны с синусом

«Физика — 11 класс»

Длина волны. Скорость волны

За один период волна распространяется на расстояние λ.

λ = vT

Длина волны — это расстояние, на которое распространяется волна за время, равное одному периоду колебаний.

Так как период Т и частота v связаны соотношением

При распространении волны:

1. Каждая частица шнура совершает периодические колебания во времени.
В случае гармонических колебаний (по закону синуса или косинуса) частота и амплитуда колебаний частиц одинаковы во всех точках шнура.
Эти колебания различаются только фазами.

2. В каждый момент времени форма волны повторяется через отрезки длиной λ.

Спустя промежуток времени Δt волна будет иметь вид, изображенный на том же рисунке второй линией.

Для продольной волны также справедлива формула, связывающая скорость распространения волны, длину волны и частоту колебаний.

Все волны распространяются с конечной скоростью. Длина волны зависит от скорости ее распространения и частоты колебаний.

Уравнение гармонической бегущей волны

Вывод уравнения волны, позволяющего определить смещение каждой точки среды в любой момент времени при распространении гармонической волны (на примере поперечной волны, бегущей по длинному тонкому резиновому шнуру).

Ось ОХ направлена вдоль шнура.
Начало отсчета — левый конец шнура.
Смещение колеблющейся точки шнура от положения равновесия — s.
Для описания волнового процесса нужно знать смещение каждой точки шнура в любой момент времени:

s = s (х, t).

Конец шнура (точка с координатой х = 0) совершает гармонические колебания с циклической частотой ω.
Колебания этой точки будут происходят по закону:

s = s_m sinc ωt

Если начальную фазу колебаний считать равной нулю.
s_m — амплитуда колебаний.

Колебания распространяются вдоль оси ОХ со скоростью υ и в произвольную точку с координатой х придут спустя время

Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ.

Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой s_m, но с другой фазой:

Это и есть уравнение гармонической бегущей волны, распространяющейся в положительном направлении оси ОХ.

Используя уравнение можно определить смещение различных точек шнура в любой момент времени.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Механические волны. Физика, учебник для 11 класса — Класс!ная физика

🎥 Видео

Урок 375. Стоячие волныСкачать

Физика. 11 класс. Упругие механические волны. Уравнение бегущей и стоячей волны /16.11.2020/Скачать

Упругие механические волны. 1 часть. 11 класс.Скачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

10й класс; Физика; "Уравнение плоской волны"Скачать

Упругие механические волны. 2 часть. 11 класс.Скачать

Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать

Волны. Основные понятия. Решение задач.Задача 1Скачать

Лекция 2 ВолныСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

🌊 Продольные и поперечные волны ⚛ ФизикаСкачать

Стоячие волны. 11 класс.Скачать

Физика 11 класс (Урок№2 - Механические волны.)Скачать

Галилео. Эксперимент. Стоячая волнаСкачать

образование стоячих волнСкачать

Якута А. А. - Механика - Волновое уравнение. Механические волны. Скорость распространения волнСкачать

5.6 Механические волны. Виды волнСкачать