- Определение опорных реакций
- Построение эпюр
- iSopromat.ru
- Задача
- Пример решения
- Решение задач, контрольных и РГР
- Расчет прогиба балки методом начальных параметров
- Теория по методу начальных параметров
- Выбор базы и обозначение системы координат
- Универсальное уравнение прогибов для балки
- Учет распределенной нагрузки
- Граничные условия
- Пример расчета прогиба балки
- Подготовительный этап
- Расчет прогиба
- 💡 Видео
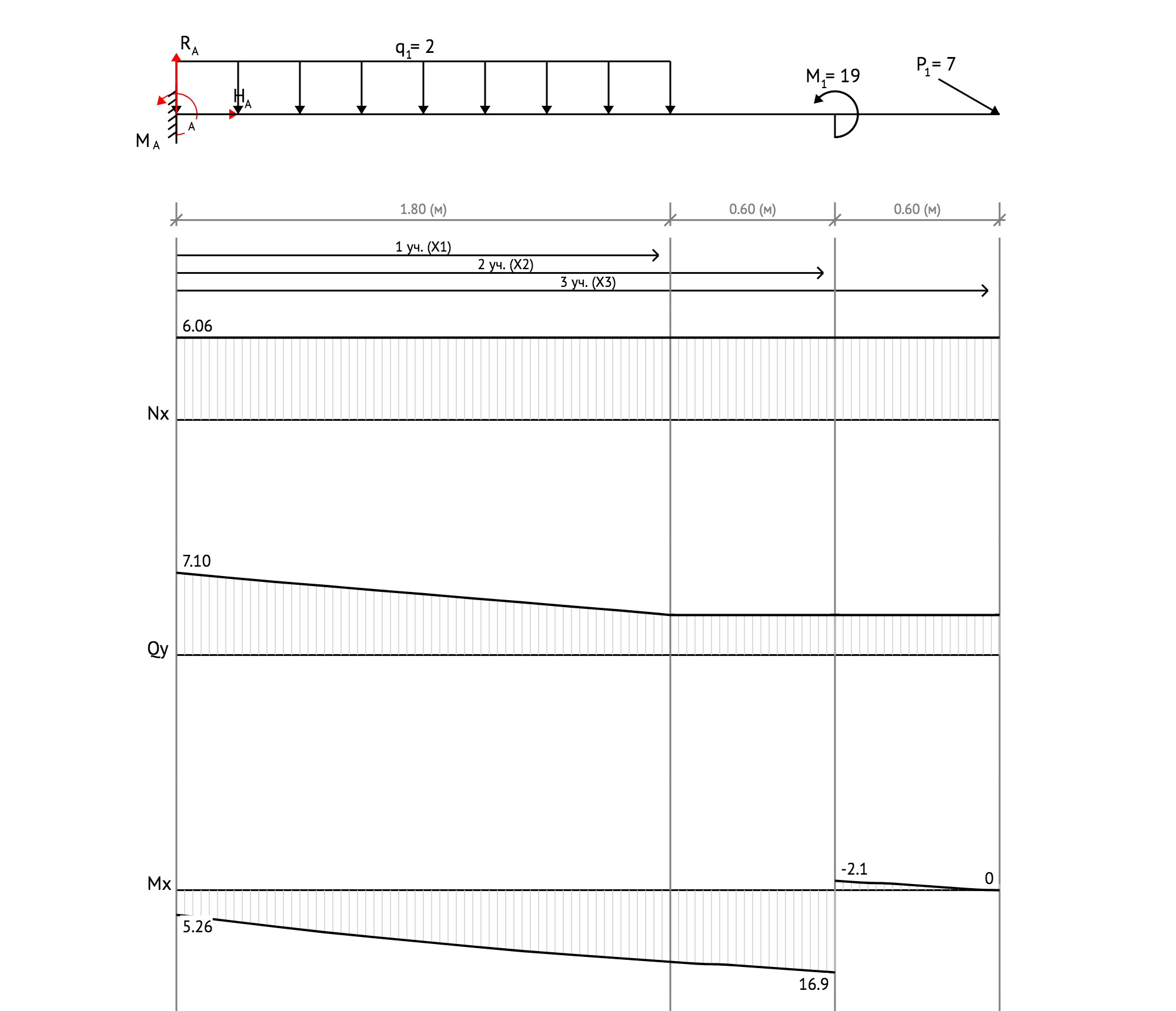
Определение опорных реакций
Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
1. На балку наложена связь в точке A (слева) типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (HA, RA, MA).
2. Определим реакции опор в соответствии с уравнениями равновесия балки: ΣFx=0, ΣFy=0, ΣMA=0.
ΣFx=0: HA + P1*cos(30)=0
ΣFy=0: RA — q1*1.8 — P1*sin(30)=0;
ΣMA=0: MA — q1*1.8*(1.8/2) + M1 — 3*P1*sin(30)=0;
3. Решаем полученную систему уравнений, находим неизвестные:
HA=- P1*cos(30)=- 7*0.8660=-6.06 (кН), так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону.
RA=q1*1.8 + P1*sin(30)=2*1.8 + 7*sin(30)=7.10 (кН)
MA=q1*1.8*(1.8/2) — M1 + 3*P1*sin(30)=2*1.8*(1.8/2) — 19 + 3*7*sin(30)=-5.26 (кН*м), так как момент отрицателен, на расчетной схеме направим его в противоположную сторону.
4. Выполним проверку, составив дополнительное моментное уравнение отоносительно свободного конца балки:
— 3*RA — MA + q1*1.8*(1.2+1.8/2) + M1 + 0*P1*sin(30)=- 3*7.10 — 5.26 + 2*1.8*(1.2+1.8/2) + 19.00 + 0*7*sin(30)=0
Построение эпюр
Рассмотрим второй участок 1.8 ≤ x2
SOPROMATGURU.RU © 2022. Все права защищены Авторские права
Видео:Балка. Реакции в заделке. Реакции опор. Сопромат.Скачать

iSopromat.ru
Пример решения задачи по расчету реакций опоры в жесткой (глухой) заделке стальной балки, нагруженной поперечной силой F, сосредоточенным моментом m и равномерно распределенной нагрузкой q.
Видео:Определение реакций опор в жесткой заделке консольной балкиСкачать

Задача
Рассчитать величину и направление опорных реакций в жесткой заделке консольной балки нагруженной заданной системой внешних нагрузок.
Видео:Определение опорных реакций в заделке ( балка ). СопроматСкачать

Пример решения
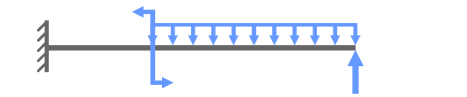
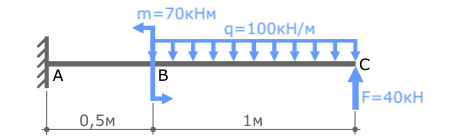
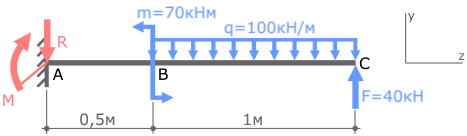
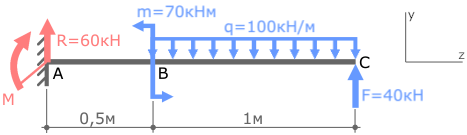
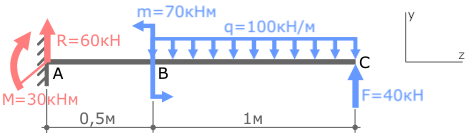
Покажем значения нагрузок и продольные размеры балки, обозначим ее характерные сечения буквами A, B и C.
В случае плоского поперечного изгиба в жесткой заделке консольной балки могут иметь место только две опорные реакции:
- Поперечная сила R
- Изгибающий момент M
На данном этапе решения задачи эти реакции можно направить в любую сторону.
Короткое видео о реакциях в заделках:
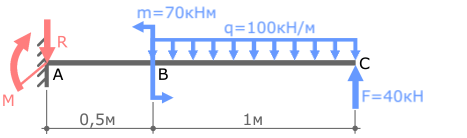
Определим величину, а заодно и истинное направление опорных реакций.
Зададим систему координат y-z.
Для нахождения двух реакций нам понадобятся два уравнения равновесия.
Балка не перемещается вверх-вниз, поэтому сумма проекций всех сил на ось y должна равняться нулю.
Проецируя все силы на ось y получаем первое уравнение:
Откуда находим величину реакции R
Знак «-» в ответе говорит о том, что реальное направление реакции R противоположно выбранному вначале.
Поэтому изменим направление силы и соответственно ее знак на противоположные.
Второе уравнение статики получим из условия, что балка не вращается, так как сумма моментов приложенных к ней тоже равнв нулю.
Отсюда находим опорный момент M
Положительный результат показывает, что выбранное наугад направление момента М оказалось верным, то есть перенаправлять его не нужно.
Полученные значения опорных реакций можно легко проверить.
Для этого запишем уравнение суммы моментов относительно точки B или C:
и подставив в него полученные значения, мы должны получить сумму равную нулю
Так и есть! Значит опорные реакции определены верно.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Решение задач, контрольных и РГР
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Видео:Техническая механика/Определение реакций в жесткой заделке.Скачать

Расчет прогиба балки методом начальных параметров
В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.
Видео:Сопромат.Построение эпюр в балке с жесткой заделкой.Дмитрий Тимофеев.я в вк https://vk.com/id4682924Скачать

Теория по методу начальных параметров
Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:
Выбор базы и обозначение системы координат
Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:
Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.
Универсальное уравнение прогибов для балки
После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): 
- E – модуль упругости;
- I – момент инерции;
- Vk – прогиб сечения K;
- VO – прогиб сечения O;
- θO – угол поворота сечения О.
Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.
Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае Vk, который дополнительно умножается на жесткость балки — EI:
Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθO всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.
Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.
Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:
В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.
Учет распределенной нагрузки
Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.
Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.
Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:
Граничные условия
Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: VK, V O и θO. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть VO=0 и θO=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.
Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах .
Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.
Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:
Видео:Определение опорных реакций в заделке консольной балкиСкачать

Пример расчета прогиба балки
Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·10 5 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см 4 ). Рассчитывать будем прогиб свободного торца, находящегося слева.
Подготовительный этап
Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:
В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:
Расчет прогиба
Записываем граничные условия для заданной расчетной схемы:
VA = 0 при x = 6м
θA = 0 при x = 6м
Напомню, что нас, в этом примере, интересует прогиб сечения O (VO). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:
В полученном уравнении, у нас содержится две неизвестные величины: искомый прогиб VO и угол поворота этого сечения — θO:
Таким образом, чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае, для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.
💡 Видео
Определение опорных реакций в балке (балка с жесткой заделкой)Скачать
ПРОЛЕТ 7 метров ДЕРЕВЯННЫМИ балками?Скачать

БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Жесткая заделкаСкачать
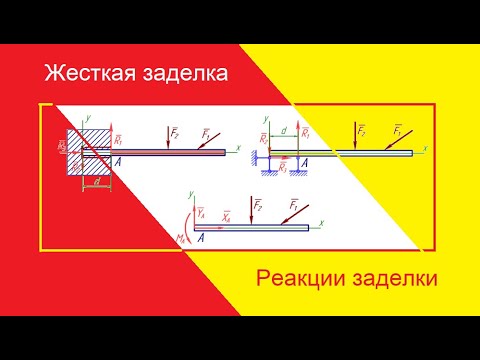
Определение реакций опор в балке. Сопромат.Скачать

BC: Расчет консолей (балконов) и консольных балокСкачать

Ломаем железобетонную балку. Проверка расчетов.Скачать

Теормех Статика Определение опорных реакций балки на жёсткой заделке (задача №3)Скачать

Проверка опорных реакций балкиСкачать

Теормех Статика Определение опорных реакций в балке на жёсткой заделке (№6)Скачать

Определение реакций жесткой заделки консольной балкиСкачать

Определение реакций опор простой рамыСкачать