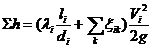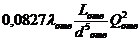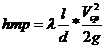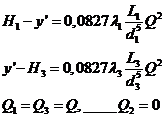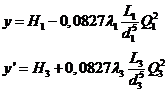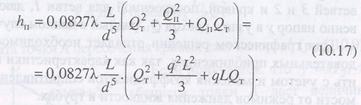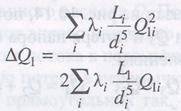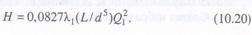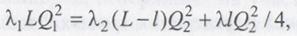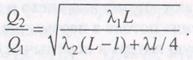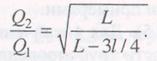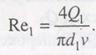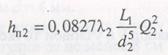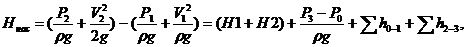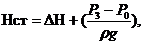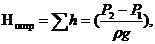Уравнение баланса напоров для трубопровода (4 видео)

Уравнение баланса напоров

Целью одного из наиболее распространенных видов гидравлического расчета является определение потерь напора при перемещении жидкости по трубопроводу.

Найдем потери участка трубопровода длиной l и диаметром D, с нефтеперекачивающей станцией (НПС) в начале. В основе расчета потерь напора используется известное уравнение Бернулли, имеющее вид

, (6.1)

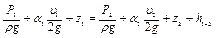
где Р₁ и Р₂ – давление в начальном и конечном сечениях трубопровода, соответственно; z₁ и z₂ – высотные отметки этих сечений; υ₁ и υ₂ – средние скорости потока в них; h_1-2 – потери напора на участке (на трение и местные сопротивления).

Поскольку, расход и диаметр участка постоянны, то скорость потока в трубопроводе также будет неизменной, и скоростные составляющие уравнения обычно исключаются ввиду равенства.

Т.к. МН характеризуется значительной протяженностью, то для упрощения расчета потери с точностью достаточной для инженерных расчетов принимают

h_м – потери напора на местных сопротивлениях, h_л – потери напора на преодоление сил вязкостного трения

Тогда полные потери по формуле Блазеуса составят

. (6.3)

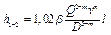
С учетом вышесказанного уравнение Бернулли примет вид

(6.4)

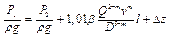
В магистральном нефтепроводе давление в перекачиваемой среде создается и поддерживается с помощью насосов, расположенных на НПС. Это давление является избыточным. Согласно основному уравнению гидростатики, оно равно

, (6.5)

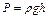
Тогда напор, развиваемый насосом (НПС) найдется как

. (6.6)

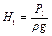
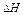
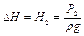
Соответственно остаточный напор в конечном сечении участка нефтепровода будет равен

. (6.7)

С другой стороны начальный напор Н₁, складывается из подпора Н_п, необходимого для безкавитационной работы основных центробежных насосов, напора, развиваемого основными насосами НПС Н_ст и внутристанционных потерь h_вн в обвязке перекачивающего оборудования (принимается 15м):

. (6.8)

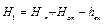
Тогда уравнение Бернулли после изменений примет вид

, (6.9)

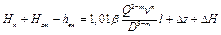
Данное уравнение называется уравнением баланса напоровдля одного перегона. Если перекачка ведётся «из насоса в насос», когда подпорные насосы необходимы только на головной нефтеперекачивающей станции (ГНПС), а подпором для ПНПС будет ΔН, то величина остаточного напора должна быть не меньше допустимой высоты всасывания ΔН_д из условия безкавитационной работы основных насосов

(6.10)

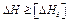
Также напор развиваемый станцией (с учетом подпора) не должен превышать допустимого Н_доп из условия прочности трубопровода

(6.11)

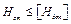
Для магистрали в целом уравнение баланса напоров будет выглядеть следующим образом

, (6.12)

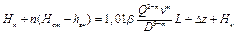
где L – длина всей магистрали, м; n – количество НПС; Н_к – напор в конце магистрали, учитывающий потерю напора в трубопроводах конечного пункта h_кп и высоту уровня взлива Н_р в резервуаре, Н_к принимают от 20 до 40 метров.

Таким образом, согласно уравнения баланса напоров, напоры, развиваемые насосными станциями, расходуются на:

а) потери напора на трение;

б) потери напора на местные сопротивления;

в) на преодоление разницы высот конца и начала перегона;

г) на подпор между станциями или на обеспечение Н_к.

Содержание

Уравнение баланса напоров для трубопровода
Проектирование и эксплуатация магистральных нефтепроводов (стр. 10 )
5.3.2 Уравнение баланса напоров
5.3.3 Особенности технологического расчёта МН с промежуточными перекачивающими станциями
5.3.4 Решение уравнения баланса напоров
5.4.1 Изменение пропускной способности МН в процессе эксплуатации
5.4.2 Практика изменения режимов перекачки
5.4.3 Классификация методов регулирования
5.4.4 Дискретное регулирование характеристик НПС
🌟 Видео

Видео:Закон БернуллиСкачать

Уравнение баланса напоров для трубопровода

11. РАСЧЕТ СЛОЖНЫХ ТРУБОПРОВОДОВ(1-я часть)

11.1.Типы сложных трубопроводов. Три задачи по расчету сложных трубопроводов.

11.2 Допущения для решения систем уравнений.

11.3. Трубопроводы с параллельными ветвями.

11.4. Приемы решения системы уравнений.

11.5 Аналитический метод решение системы уравнений

11.6 Графический метод решение системы уравнений

11.7 Трубопроводы с концевой раздачей

11.8. Трубопроводы с непрерывной раздачей.

11.9. Трубопроводы с кольцевыми участками

11.10. Трубопроводы с насосной подачей жидкости. Нахождение рабочей точки

Трубопровод называется сложным, если он имеет разветвленные участки, и состоит из нескольких труб-ветвей, между которыми распределяется жидкость.

Узлами сложного трубопровода называются сечения, в которых смыкаются несколько ветвей.

11.1.Типы сложных трубопроводов.

Три задачи по расчету сложных трубопроводов.

Различают следующие основные типы сложных трубопроводов:

а) с параллельными ветвями, б) с концевой раздачей жидкости, в) с непрерывной раздачей жидкости, д) с кольцевыми участками.

В практике встречаются также сложные трубопроводы комбинированного типа.

Можно выделить три основные группы задач расчета сложных трубопроводов.

1-я задача. «Определение размеров труб по заданным в них расходам и перепадам напоров в питателях и приемниках».

2-я задача. «Определение перепадов напоров в питателях и приемниках по заданным расходам в трубах заданных размеров».

3-я задача. «Определение расходов в трубах заданных размеров по известным перепадам напоров».

Встречаются также задачи смешанного типа.

Для решения этих задач составляется система уравнений, которая устанавливает функциональные связи между параметрами, характеризующими потоки жидкости в трубах, т.е. между размерами труб, расходами жидкости и напорами. Эта система включает:

1) уравнение баланса расходов для каждого узла;

2) уравнение баланса напоров (уравнений Бернулли) для каждой ветви трубопровода.

11.2. Допущения для решения систем уравнений.

1) Обычно сложные трубопроводы являются длинными, в уравнениях Бернулли можно пренебрегать скоростными напорами.

2) Можно, принимать полный напор потока в каждом расчетном сечении трубопровода практически равным гидростатическому и выражая его высотой пьезометрического уровня над принятой плоскостью сравнения.

3) В сложных трубопроводах можно пренебрегать относительно малыми местными потерями напора в узлах.

Эти допущения упрощают расчеты, поскольку позволяет считать одинаковыми напоры потоков в концевых сечениях труб, примыкающих к данному узлу, и использовать в уравнениях Бернулли понятие напора в данном узле.

Потери напора в трубах выражаются формулой

которую для расчета можно привести к виду

(11.1)

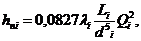
где l_i и d_i — длина и диаметр трубы, ξ _ik — коэффициент местного сопротивления, V_i — средняя скорость потока в трубе, λ i — коэффициент сопротивления трения, Li — приведенная длина трубы (учитывает местные сопротивления с помощью их эквивалентных длин l_i _э , Li = l_i + l_i _э, здесь l_i _э = Σ _k ξ _ik d_i / λ _i ) .

Числовой множитель в формуле (11.1) равен 16/(π 2 *2 g ), где g — ускорение свободного падения выражено в м/ c 2 .

Конкретный вид системы расчетных уравнений и способы ее решения определяются типом сложного трубопровода и характером поставленной задачи. Для получения однозначного решения система расчетных уравнений должна быть замкнутой, т.е. число независимых неизвестных в ней должно быть равно числу уравнений.

11.3. Трубопроводы с параллельными ветвями.

В таких трубопроводах разветвленные участки состоят из нескольких труб, соединяющих два данных узла .

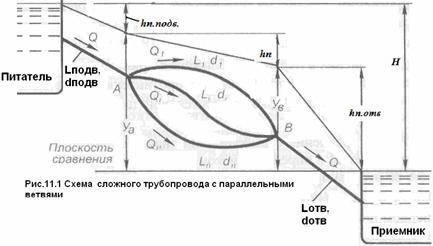
Общая схема трубопровода с параллельными ветвями (рис. 11.1) включает питатель, трубу, подводящую жидкость к разветвленному участку, параллельные трубы на разветвленном участке, трубу, отводящую жидкость от разветвленного участка, приемник.

В частных случаях некоторые элементы этой схемы могут отсутствовать.

Уравнение баланса расходов в узле А

где индекс i относится к любой из параллельных труб.

Уравнение баланса расходов в поводящей и отводящей магистралях

— расход в подводящей и отводящей трубах (магистральный расход).

В соответствии с допущением 1: в длинных трубах скоростными напорами можно пренебрегать.

Потеря напора в каждой из параллельных труб одинакова и практически равна разности h пьезометрических уровней в узлах ( рис. 11.1):

Рассмотрим более подробно уравнение баланса расходов и напоров в параллельном соединении.

Составляя уравнения Бернулли для каждой из труб, получаем уравнения баланса напоров из системы трех уравнений

< у_А -у_В = h _п (уравнения Бернулли для параллельных труб) (11.4)
ув = h _п.отв,

где Н — напор трубопровода — перепад напоров в питателе и приемнике; у_А и у_В — напоры в узлах А и В, отсчитанные от уровня в приемнике.

Сравнивая уравнения Бернулли, записанные для параллельных труб, приходим к соотношению

_где h _п _{n —}_п_{отери в параллельных трубах.}
Это соотношение показывает, что потери напора в параллельных трубах равны между собой. Следовательно, потеря напора в разветвленном участке между узлами равна потере напора в любой из параллельных труб, соединяющей эти узлы.

Суммирование потерь напора в последовательно расположенных участках сложного трубопровода (подводящая труба, разветвленный участок, отводящая труба) приводит к соотношению, которое называется балансом напоров в сложном трубопроводе с параллельными ветвями.

Таким образом, система расчетных уравнений с учетом формулы (11.1) может быть приведена к системе вида

< = = (11.7)

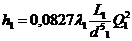
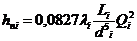
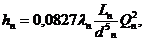
Н = +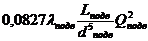

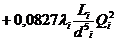
Поскольку в длинных трубах скоростными напорами мы пренебрегаем, потеря напора в каждой из параллельных труб практически равна разности h пьезометрических уровней в узлах: h _п1 =… = h _п _i =…= h _п _n = h .

C истема уравнений (11.7) позволяет решить любую из сформулированных выше задач.

11.4. Приемы решения системы уравнений.

1.Решение этой системы (11.7) выполняют методом последовательных приближений, так как, не зная размеров труб или идущих по ним расходов, нельзя точно определить коэффициенты сопротивления λ _i ,ξ _ik в этих трубах. Для решения в первом приближении принимают, что в трубах имеет место квадратичный закон сопротивления. Значения λ _i и ξ _ik определяются только относительной шероховатостью труб.

2. Решив уравнения с выбранными значениями коэффициентов сопротивлений и определив искомые величины, повторяют решение во втором приближении, пользуясь более точными значениями и результатами первого приближения. Приближения повторяют до близкого совпадения(5-7%) результатов. Обычно уже второе приближение оказывается достаточно точным.

3. При аналитическом решении системы уравнений (11.7) удобно заменить пучок параллельных труб одной эквивалентной трубой, которая пропускает весь расход, проходящий через параллельные трубы, при потерях напора, равных потерям напора на разветвленном участке.

Размеры эквивалентной трубы (диаметр d и длина L э) связаны с размерами параллельных ветвей соотношением

(11.8)

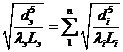
(При этом d э и λэ можно выбрать, как средние величины, или, как d э и λэ в подводящей или отводящей ветвях, а L э найти.)

4. При расчете этим способом схема трубопровода с параллельными ветвями приводится к схеме простого трубопровода, в который эквивалентная труба входит как один из последовательных участков. Для схемы трубопровода, показанной на рис. 11.1, уравнение баланса напоров в этом случае имеет вид

Н = 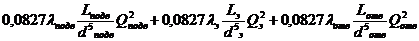(11.9)

11.5 Графический метод решение системы уравнений

для трубопровода с заданными размерами.

11.5.1 Последовательность решения системы уравнения при графическом методе решения.

1. Построение характеристик всех труб с использованием уравнения (11.1). При построении в зависимости от ламинарного или турбулентного режима движения жидкости в трубе выбирается показатель степени при Q и величина коэффициента λ . При турбулентном течении в трубе ее характеристика является квадратичной параболой; при ламинарном течении в длинной трубе — практически прямой зависимостью. Характеристика представляет собой зависимость потерь напора в трубе от расхода.

1.1 Для турбулентного режима

-парабола, (11.10)

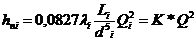
1.2.Для ламинарного движения Формула Вейсбаха—Дарси

где λ — коэффициент потерь на трение в трубе, для ламинарного режима λ_л =64/ Re , скорость через расход: Q = V *(π/4) d 2 , выражение для потерь при ламинарном движении

(11.11).

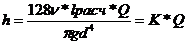
Характеристики параллельно работающих ветвей затем суммируют согласно уравнениям (11.6) и (11.7), т.е. путем сложения абсцисс кривых (расходов) при одинаковых ординатах (напорах). Полученную в результате такого суммирования характеристику разветвленного участка можно рассматривать как характеристику эквивалентной трубы, заменяющей данные параллельные.

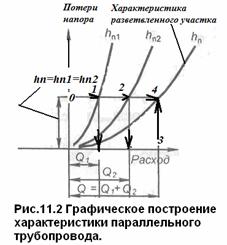
На рис. 11.2 построена характеристика разветвленного участка трубопровода, со- стоящего из двух параллельных труб. h _п1 и h _п2 –графики потерь в параллельных ветвях, построенные по формулам (10.11).

В параллельных ветвях потери равны h п1 = h п2, следовательно и у разветвленного (эквивалентного) заменяющего их участка трубопровода, потери такие же h п1 = h п2= h п.

1.3. Откладываем на оси абсцисс величину потерь h п1 = h п2= h п, точка — 0

1.4 Проводим линию параллельную оси ординат, в точках 1 и 2 получаем значения расходов: Q ₁, Q ₂, суммируем их и получаем точку -3 для построения графика потерь эквивалентного участка, точку — 4. Также строим и другие точки.

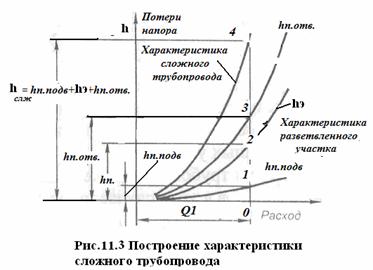
11.5.2 Построение характеристики сложного трубопровода.

Характеристику эквивалентного участка суммируют с характеристиками подводящей и отводящей труб и получают характеристику сложного трубопровода

2.1 На график следует нанести характеристики: подводящей, эквивалентной и отводящей магистралей.

2.2 На оси ординат откладывают величину расхода, выходящего из питателя – Q ₁, точка — 0.

2.3. По расходу Q 1 определяют потери в подводящем трубопроводе – точка -1, напор — h п. подв , в эквивалентном – точка -2 — h э, в отводящем – точка – 3, h п. отв .

2.3. Сложением ординат (напоров) h п. подв + h э + h п. отв при одинаковом расходе – Q 1, получим характеристику сложного трубопровода – точка 4 (рис. 11.3).

Остальные точки можно получить при значениях Q Q ₁.

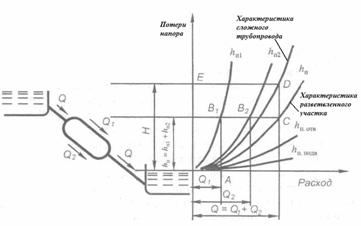
11.5.3 Пример использования графического расчета сложного трубопровода с двумя параллельными ветвями показан на рис. 11.4.

Определение потребного напора сложного трубопровода по характеристикам сложного трубопровода по заданному расходу в одной из ветвей, например, подводящей, отводящей или по расходу в одном из параллельных участков.

Для задачи известный расход в одной из параллельных ветвей, например, в первой — Q ₁, нужно отложить на оси абсцисс и через полученную точку А провести вертикаль до пересечения с характеристикой первой ветви, точка B ₁. Ордината h _п1, точки В_1, выражает потери напора в параллельных ветвях : h _п1 = h _п2 = h _п_.

Через точку В₁ провести горизонталь до пересечения с характеристикой второй параллельной ветви разветвленного участка, то получим точку В₂, абсцисса которой равна расходу Q ₂ .

Складывая расходы, получаем суммарный расход Q = Q ₁ + Q ₂ через параллельный участок.

На пересечении абсциссы Q и ординаты h п, получаем точку С — это точка совместной характеристики разветвленного участка.

Восстановив вертикаль до пересечения с характеристикой сложного трубопровода, получим точку D , ордината которой выражает искомый потребный напор Н.

2. Определение расходов во всех трубах по заданному располагаемому напору определить.

2.1 На оси ординат отложить известный напор Н — точка Е.

2.2. Через точку Е провести горизонталь до пересечения с суммарной характеристикой сложного трубопровода точка — D . Абсцисса этой точки D выражает суммарный расход

2.3.Через точку D провести вертикаль до пересечения с характеристикой разветвленного участка, ордината полученной точки С будет соответствовать потерям напора в каждой из параллельных ветвей.

2.4 Через точку С провести горизонталь до пересечения с характеристиками ветвей, то получим точки В₂ и В₁, абсциссы которых являются расходами Q ₂ и Q ₁ в ветвях.

Если характеристики построены с учетом коэффициентов сопротивления трения и коэффициентов местных сопротивлений в зависимости от режимов течения жидкости в трубопроводах, то отпадает необходимость в последовательных приближениях, что является значительным преимуществом графического метода.

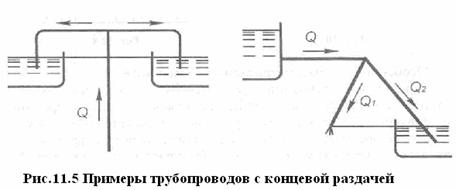
11.6. Трубопроводы с концевой раздачей.

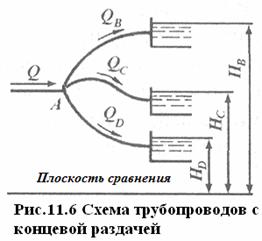
Соотношения (11.2) и (11.4) могут быть использованы не только для расчета сложных трубопроводов с параллельными ветвями, но и для расчета сложных трубопроводов с концевой раздачей в тех случаях, когда перепады напоров в ветвях, расходящихся из одного узла, оказываются равными. На рис. 11.6 показаны некоторые схемы таких трубопроводов.

11.6.1 Аналитический метод решения.

В трубопроводах этого типа жидкость, поступающая к узлам из питателей, распределяется между несколькими ветвями, по которым она направляется к приемникам с различными напорами жидкости, см. рис. 11.6, где жидкость, подводимая к узлу А, раздается по трубам в приемники с напорами Нв, Н _C ., Н _D .

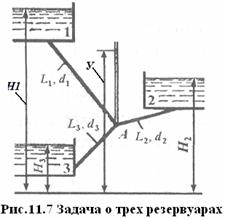
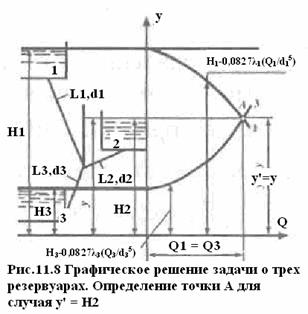
Расчет трубопровода с концевой раздачей рассмотрим на простейшей схеме трубопровода, соединяющего три резервуара и имеющего один узел (рис. 11.7). Особенностью рассматриваемой схемы является то, что система расчетных уравнений получается различной в зависимости от направления потока в трубе, соединяющей узел со средним резервуаром 2.

Верхний резервуар 1 всегда является питателем, и жидкость поступает из него к узлу. Нижний резервуар 3 всегда является приемником, и жидкость поступает к нему от узла.

Резервуар 2 может быть как приемником, так и питателем. Направление потока в трубе 2 определяется соотношением между напором у в узле и напором Н₂ в среднем резервуаре. В зависимости от этого соотношения возможны три случая распределения расходов в трубах и в соответствии с этим три различные системы расчетных уравнений.

1. Если напор у в узле меньше напора Н2 в резервуаре 2 (у Н2), то жидкость из резервуаров 1 и 2 перетекает в резервуар 3, и система уравнений для решения задачи имеет вид,

случай у Н2: 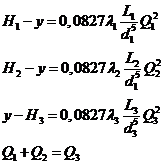> (11.13)

2.Если напор у > H 2, то жидкость из резервуара 1 перетекает в резервуары 2 и 3 , и расчетная схема принимает вид

у > H 2 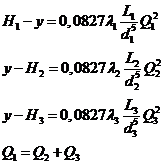(11.14)

3. Если у = Н₂, расход Q ₂ = 0, Q ₁= Q ₂ = Q и жидкость перетекает из резервуара 1 в резервуар 3.

Расчетная система уравнений имеет вид

> (11.15)

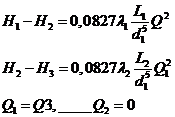
Если система включает трубы, которые оканчиваются сходящимися насадками, открытыми в атмосферу, то при составлении уравнений баланса напоров для таких труб следует учитывать скоростные напоры на выходе из насадков.

Системы расчетных уравнений выбирают в зависимости от постановки задачи. Направление потока в трубе 2 может быть наперед задано условиями задачи или же, если оно заранее неизвестно, должно определяться в процессе самого решения.

Рассмотрим случай, когда известными в задаче являются напоры в резервуарах и размеры всех труб; требуется определить расходы в трубах.

Решение следует начинать с определения направления потока в трубе 2, для чего используется специальный прием «выключения ветви».

При этом вычисляют напор у’ в узле при выключенной трубе 2, т.е. когда Q ₂ = 0 и Q 1= Q 3. Составляя уравнения Бернулли для труб 1 и 3 и, решая их относительно у’ , получаем

(11.16)

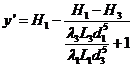
3.1.Если это уравнение дает значение у’ задачи нужно воспользоваться системой уравнений (11.13).

3.2. Если у’> Н2, то при включении трубы 2 имеем второй случай, и для решения задачи используются уравнения системы (11.14).

3.3. Если у’ = Н2, то при включении трубы 2 расход в ней равен нулю, и расчет производится соответственно третьему случаю по уравнениям (11.15).

Так как расходы в трубах являются в этой задаче искомыми неизвестными и, следовательно, значения коэффициентов сопротивлений труб заранее точно определить нельзя, аналитическое решение проводится методом последовательных приближений.

11.6. Трубопроводы с концевой раздачей.

11.6.2 Графический метод решения.

Рассмотренная задача может быть решена и графическим методом, т.е. путем графического решения приведенных выше расчетных систем уравнений.

Идея графического решения заключается в определении напора у в узле, при котором удовлетворяется условие баланса расходов.

1. Сначала определяют напор у’ в узле при выключенной трубе 2, для чего строят кривые у = f ( Q ) для ветвей 1 и 3 у’ = f ( Q ) согласно уравнениям

2. Ордината точки А пересечения кривых дает напор у’ (рис. 10.9).

2.1.Если у’ = Н₂, то абсцисса точки А дает величину действительного расхода в ветвях 1 и 3 ( Q ₁ = Q ₃= Q ). Расход Q ₂=0 при этом равен нулю.

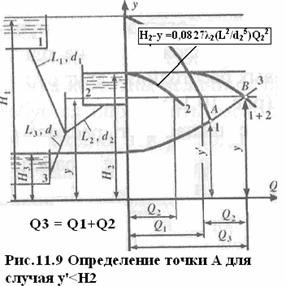
2.2 Если у’ Н2, то имеет место распределение потоков в ветвях, соответствующее первому расчетному случаю: Q 1+ Q 2 = Q 3.

2.2.1 Для определения расходов в этом случае следует построить кривую у = f ( Q ) для ветви 2 согласно второму уравнению системы (11.13)

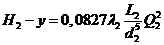
2.2.2 Затем сложить кривые, построенные для ветвей 1 и 2 согласно последнему уравнению той же системы(т.е. Q 3 = Q 1+ Q 2 (рис. 11.9).

2.2.3.Ордината и абсцисса точки В пересечения суммарной кривой ветвей 1 и 2 с кривой ветви 3 дают действительный напор в узле « Y « и расход Q 3, равный в этом случае Q 1 + Q 2.

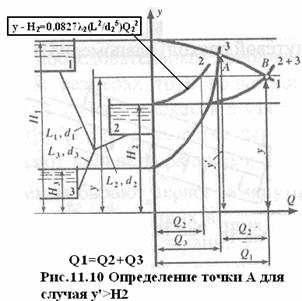
2.3. Если у’> Н2 (рис. 11.10), то имеет место распределение потоков в ветвях, соответствующее второму расчетному случаю Q 1 = Q 2+ Q 3.

2.3.1 Для определения расходов следует построить кривую у = f ( Q ) для ветви 2 согласно второму уравнению системы y — H ₂=0,0827 λ ₂( L 2 / d ₂ 5 ) Q ₂ 2 и сложить кривые для ветвей З и 2 согласно последнему уравнению этой же системы.

2.3.2 Ордината и абсцисса точки В пересечения суммарной кривой ветвей З + 2 и кривой, построенной для ветви 1, дают соответственно напор в узле « Y « и расход (2, равный в данном случае Q 1= Q 2 + Q 3.

При графическом решении отпадает необходимость в последовательных приближениях, так как характеристики можно строить с учетом изменения коэффициентов сопротивлений в зависимости от режимов движения жидкости в трубах.

Заметим, что в практике расчетов возможны такие постановки задач, при которых расчетная система уравнений оказывается неопределенной, и решение приобретает неоднозначный характер.

Такой, например, является задача проектирования трубопровода с концевой раздачей (см. рис. 11.7), когда требуется определить размеры ветвей (обычно их диаметры) так, чтобы при заданных напорах в резервуарах обеспечить подачу из верхнего резервуара 1 в нижние резервуары 2 и 3 заданных расходов жидкости.

При этом можно видеть, что в расчетной системе уравнений (11.13) число искомых неизвестных больше числа уравнений. Для решения задач такого типа используют дополнительные условия технико-экономического характера.

11.7. Трубопроводы с непрерывной раздачей.

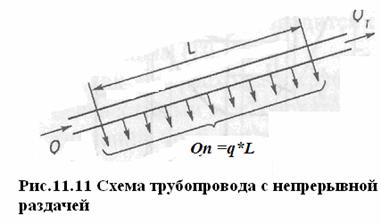
Трубопроводом с непрерывной раздачей называется такой трубопровод, в котором на некоторой длине L часть расхода Q п (путевой расход) равномерно потребляется в большом числе пунктов, расположенных на одинаковых расстояниях друг от друга (рис. 11.11).

Остальная часть расхода Q т (транзитный расход) транспортируется через участок L в последующие участки трубопровода. Расчет трубопроводов с непрерывной раздачей выполняют в предположении, что жидкость отбирается из трубопровода непрерывно и равномерно с интенсивностью q (л/с)*м) по всей длине L разветвленного участка. При этом путевой расход

Q п = q * L (1 1 .15)

C уммарный расход в начальном сечении участка

Q = Q п + Q т = q * L + Q т. (11.16)
Потерю напора на разветвленном участке L трубопровода можно подсчитать по формуле

11.8. Трубопроводы с кольцевыми участками

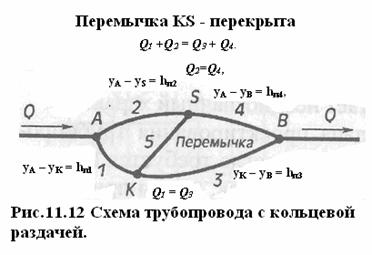
Кольцевой разветвленный участок представляет собой в простейшем случае две параллельные трубы между узлами А и В с одной или несколькими перемычками, соединяющими промежуточные сечения этих труб (рис. 10.13).

По перемычкам некоторое количество жидкости перетекает из одной трубы в другую. Направление потока в перемычке определяется величинами напоров в соединяемых перемычкой сечениях.

Жидкость может подаваться в кольцевой разветвленный участок или отбираться из него через узлы А и В смыкания участка с подводящей и отводящей трубами или через узлы К и S на концах перемычек.

11.8.1.Аналитический метод расчета трубопровода с кольцевыми участками применяют метод последовательных приближений.

1. Например, если при заданных размерах труб кольцевого участка известны величины притока и отбора жидкости в узлах и требуется определить расходы в трубах, то в качестве первого приближения эти расходы Q ₁ _i задают удовлетворяющими условиям баланса расходов в узлах.

2. Затем выбирают первое замкнутое кольцо разветвленного участка и для всех входящих в него труб вычисляют потери напора. Расходы считаются заданными правильно, если алгебраическая сумма потерь напора в кольце равна нулю. В противном случае следует повторить выкладки при измененных расходах в трубах:

Поправка Δ Q должна удовлетворять уравнению

Подбор расходов следует продолжать до тех пор, пока алгебраическая сумма потерь напора в трубах рассматриваемого кольца не станет равной нулю. Затем аналогичные вычисления повторяют последовательно для каждого из замкнутых контуров разветвленного участка.

11.8.2. Графический метод расчета кольцевых трубопроводов с заданными размерами.

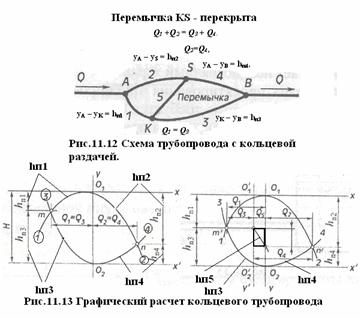
Рассмотрим такой способ применительно к схеме кольцевого участка на рис. 11.12, предполагая, что жидкость подается в кольцо через узел А и отбирается из кольца через узел В.

1. При графическом решении задачи первоначально предполагаем, что перемычка К S перекрыта. В этом предположении Q ₁ = Q ₃ и Q ₂= Q ₄, кроме того Q ₁ + Q ₂ = Q ₃ + Q ₄.

2. Для определения направления потока в перемычке составляют уравнения характеристик труб 1 — 4:

где у_А, у_К, у _S и у _B — напоры в узлах; h п — потери напора в трубах, подсчитываемые по уравнению (11.1) 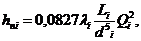. Построения выполняем в следующем порядке.

3. Если известен перепад напоров Н = у_А — у _B и требуется определить расходы в трубах, выбираем вертикальную ось у и пересекаем ее горизонтальными осями х и х’, расстояние между которыми Н. Точки пересечения обозначаем О₁ и О₂.

4. Строим кривые потерь в трубах 1, 2, 3 и 4 из точек О₁ и О₂, как показано на рис. 11.13.

5. Абсцисса точки т пересечения кривых 1 и 3 дает при этом расход в ветви АКВ( Q 1 = Q 3), а абсцисса точки п пересечения кривых 2 и 4 дает расход в ветви А S В ( Q 2 = Q 4) (см. рис. 11.13).

5. Ординаты точек т и п (см. рис.11.13), отсчитанные соответственно от осей х и х’, дают напоры, потерянные на участках 1, 2, 3 и 4.

6. По соотношению напоров, потерянных на участках 1 и 2, можно установить направление потока в перемычке после ее открытия. В случае, который показан на рис. 11.13, поток направлен от К к S (см. рис. 11.13), потому что h п3> h п4. Расход Q ₅‚ и потеря напора h _п5 в перемычке должны удовлетворять уравнениям:

Q 1 = Q 3+ Q 5; Q 4 = Q 2+ Q 5;

h п1+ h п5= h п2; (11.12)

При этом равенства Q 1+ Q 2 = Q 3 + Q 4 и h _п1 + h _п3 = h _п2 + h _п4 остаются в силе.

Для отыскания величин Q 5 и h _п5 на чертеж накладывается лист кальки, на который наносятся оси х’ и у, а также кривые h _п3 и h _п4. Калька передвигается влево, если h _п1 h _п2 или вправо, если h _п1 > h _п2 .

Сдвинув кальку влево (см. рис. 11.13), отметим точки т’ и п’ и проведем через них горизонтальные прямые. Эти прямые образуют с осями у и у’ прямоугольник. На отдельном листе кальки построим кривую h _п5 = f ( Q ₅) для перемычки. Наложим эту кальку на чертеж так, чтобы начало кривой h _п5 совпало с левым верхним углом прямоугольника.

Кальки переместим до положения, при котором кривая h _п5 пройдет через правый нижний угол прямоугольника. При этом расстояние между осями у и у’ показывает расход в перемычке, а расстояние между горизонталями, проходящими через точки m и n , соответствует потере напора в перемычке. Абсциссы точек m ’ и n ’, отсчитанные от оси у’, выражают расходы на участках, а ординаты, отсчитанные от осей х и х’, выражают потерянные на участках напоры. При этом уравнения (10.19) удовлетворяются.

При отыскании напора Н, необходимого для пропуска через данную систему заданного расхода , кальку с кривыми З и 4 и осью у накладывают на чертеж с нанесенными кривыми 1 и 2 так, чтобы оси у и У’ совпали, а затем передвигают вверх или вниз, пока сумма абсцисс точек пересечения кривых 1 и З и кривых 2 и 4 не будет изображать заданного расхода Q . После этого кальку с кривыми З и 4 передвигают вправо или влево в зависимости от получающегося направления потока в перемычке.

Накладывая кривую потерь в перемычке h _п5 = f ( Q ₅) на образовавшийся на чертеже прямоугольник так, чтобы начало располагалось в левом верхнем углу, перемещают кальки по вертикали до тех пор, пока h _п5 не станет равной h _п2 — h _п1 или h _п1 — h _п2.

Рассмотренные выше методы расчета трубопроводов проиллюстрируем некоторыми примерами.

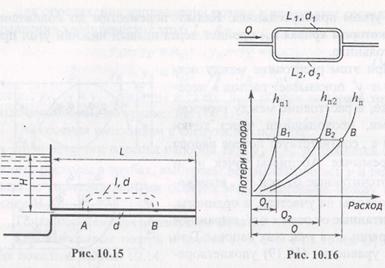
Пример 1 (рис. 11.14). Для увеличения при заданном напоре Н пропускной способности трубопровода к нему между сечениями А и В присоединяют параллельную ветвь.

Определить, во сколько раз изменится расход в трубопроводе длиной L , диаметром d , если к нему присоединена параллельная ветвь того же диаметра длиной l .

Считая трубопроводы длинными, предполагая наличие в них турбулентных потоков, имеем для случая работы одного трубопровода

Для случая работы трубопровода с параллельной ветвью
(10.21)
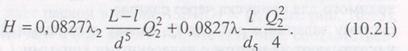
Сравнивая уравнения (10.20) и (10.2 1), получаем

Так как при неизвестных расходах вычислить точные значения λ нельзя, задачу решим приближенно. Принимая в первом приближении величины λ для всех труб одинаковыми, получаем

В частном случае при L = l имеем
Q 2/ Q 1 = 2.
Пример 2 (рис. 10.16). Найти, как распределится расход жидкости Q между двумя параллельными трубами диаметрами d 1 и d 2 длинами (приведенными) L 1 и L 2 при значениях абсолютной шероховатости труб Δ1 и Δ2.

Поскольку искомыми величинами в задаче являются расходы, целесообразно избрать графический метод решения.

Построим характеристику первой трубы согласно уравнению

задавая ряд значений Q и вычисляя h п1; соответствующие величины определяются по заданной относительной шероховатости d 1/Δ и значениям числа Рейнольдса (см. гл. 9)

В тех же осях аналогично построим характеристику второй трубы

Складывая построенные кривые по правилу суммирования характеристик параллельных труб, получим характеристику разветвленного участка.

Далее на оси расходов находим точку, соответствующую суммарному расходу Q , и проводим через нее вертикаль до пересечения с характеристикой разветвленного участка. Через полученную точку В проводим горизонталь до пересечения с характеристиками первой (точка В1) и второй (точка В2) труб. Абсциссы полученных точек пересечения выражают искомые расходы Q 1 в первой и Q 2 во второй трубах.
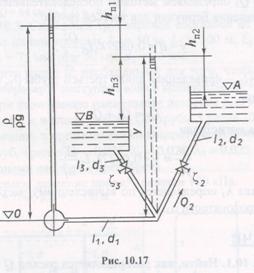
Пример З (рис. 10.17). Вода поступает из магистрали по трубам заданных размеров ( l 1, d 1, l 2, d 2, l 3, d 3) и шероховатостей (Δ1,Δ2,Δ3) в два резервуара, уровни в которых расположены на отметках А и В выше уровня оси магистральной трубы.

Определить, при каком давлении р в магистрали в верхний резервуар будет поступать расход Q 2.

По заданному расходу Q 2 и шероховатости Δ2 трубы определяем коэффициент сопротивления трения λ2 и эквивалентную длину местных сопротивлений, установленных на второй трубе l ₂ =ξ₂/ λ ₂.

Затем вычисляем напору в узловой точке трубопровода:

где L ₂ = l ₂ + l _2э — приведенная длина второй трубы.

Расход Q 3 определяем методом последовательных приближений из уравнения Бернулли для третьей трубы:

где L ₃ = l ₃ + l _3э — приведенная длина третьей трубы l ₂ =ξ₂/ λ ₂.

где величина λ₁ определяется по вычисленному расходу и заданной шероховатостиΔ₁.
11.9. Трубопроводы с насосной подачей жидкости. Нахождение рабочей точки

В машиностроении основным способом подачи жидкости является подача насосом.

Методы расчета характеристик трубопровода и насоса позволяют определить их рабочую точку.

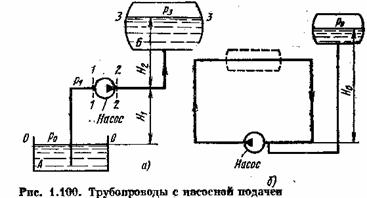
Трубопровод с насосной подачей может быть разомкнутым, когда жидкость перекачивается из одной емкости в другую (рис.11.16а) или замкнутым, когда напорный трубопровод соединен со всасывающим, и в гидросистеме циркулирует одно и то же количество жидкости (рис. 11.16б).

Рассмотрим разомкнутый трубопровод, по которому насос перекачивает жидкость, из нижнего резервуара с давлением Р₀ в верхний — с давлением Р₂ .

Геометрической высотой всасывания Н₁ называется высота расположения оси насоса относительно нижнего уровня жидкости в баке.

Трубопровод , по которому жидкость поступает к насосу, называется всасывающим трубопроводом или линией всасывания.

Геометрической высотой нагнетания Н₂ называется высота расположения оси насоса относительно верхнего уровня жидкости или относительно конечного сечения трубопровода.

Трубопровод, по которому жидкость движется от насоса, называется напорным трубопроводом или линией нагнетания.

Составим уравнение Бернулли для потока жидкости во всасывающем трубопроводе для сечений «0 – 0» и «1-1», принимая α=1:

(1.149)

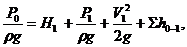
Уравнение (1.149) является основным для расчета всасывающих трубопроводов. Оно показывает, что всасывание или подъем жидкости на высоту Н₁, сообщение ей кинетической энергии и преодоление всех гидравлических сопротивлений происходит за счет использования насоса, который создает давление Р₀.

Для нормальной бескавитационной работы насоса перед входом в насос должен остался некоторый запас давления Р₁. Т.е.магистрали всасывания должны иметь минимальное сопротивление.

Возможны следующие задачи на расчет всасывающего трубопровода.

Задача 1. Даны все размеры и расход и требуется найти абсолютное давление перед входом в насос.

Решение этой задачи представляет собой поверочный расчет всасывающего трубопровода. Абсолютное давление Р₁, полученное по уравнению (1.149), сравнивают с тем, которое является минимально допустимым для данного случая.

Задача 2. Дано минимально допустимое абсолютное давление Р₁ перед входом в насос и требуется найти одну из следующих предельно допустимых величин: Р₁ _max , Q_max , d_min или P ₀ _min .

За g пишем уравнение Бернулли для движения жидкости по напорному трубопроводу, т. е. для сечений «2 – 2» и «3 – 3»:

(1.150)

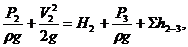
Левая часть уравнения (1.150) представляет собой энергию жидкости на выходе из насоса, отнесенную к единице веса.

Энергия жидкости перед входом в насос для сечения «1 – 1» может быть определена из уравнения (1.149):

( 1.150’ )

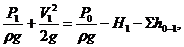
Найдем приращение энергии жидкости в насосе, т. е. определим ту энергию, которую приобретает, проходя через насос, каждая единица веса жидкости.

Энергия сообщаемая жидкости насосом называется напором насоса и обозначается обычно Н_нас.

Для нахождения напора насоса Н_нас вычтем последнее уравнение ( 1.150’ ) из уравнения (1.150):

Потери напора по длине и в местных сопротивлениях выражаются с учетом уравнения неразрывности Q = V * F = V *(π/4) d 2 , V = Q / F =4 Q /(π d 2 ), V 2 = (16* Q 2 )/(π 2 d 4 ),

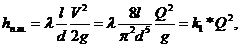
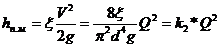
Обозначим сумму разности геометрических напоров ΔН и пьезометрического напора (Р₃-Р₀)/(ρ g ), как статический напор

и формулу (1.151) переписать так, при К=к₁+к₂:

( 1.151’ )

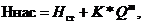
В правой части этого уравнения: сопротивления, преодолеваемые при работе насоса, их можно назвать потребным напором.

Можно сформулировать правило: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.

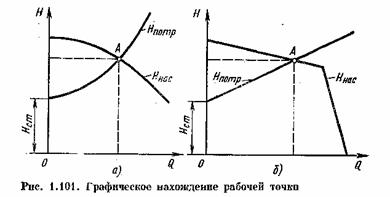
На равенстве (1.152) основывается метод расчета трубопроводов, питаемых насосом, который заключается в совместном построении, в одном и том же масштабе на одном графике двух кривых: Н_потр = f ₁( Q ), Н_нас= f ₂( Q )и в нахождении их точки пересечения(рис.1.101).

Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи или расхода жидкости при постоянной частоте вращения вала насоса. На рис. 1.101 дано два варианта графика:

а) для турбулентного режима течения в трубопроводе и центробежного насоса;

б) для ламинарного режима и объемного насоса.

Рабочей точкой называется точка пересечения кривой потребного напора и характеристики насоса, где имеется равенство потребного напора и напора насоса.

Чтобы получить другую рабочую точку, необходимо или изменить открытие регулировочного крана (вентиля, задвижки), т. е. изменить характеристику трубопровода или изменить частоту вращения вала насоса.

Данный расчетный прием для нахождения рабочей точки применим в том случае, когда частота вращения привода насоса не зависит от мощности, им потребляемой, т. е. от нагрузки на валу насоса. Например, при соединении насоса с электродвигателем переменного тока или с иным двигателем, мощность которого во много раз больше мощности насоса.

Для замкнутого трубопровода (рис. 1.100б) геометрическая высота подъема жидкости равна пулю (ΔН = 0 ), следовательно, при V ₁= V₂:

т. е. между потребным напором и напором, создаваемым насосом, справедливо то же равенство.

Замкнутый трубопровод обязательно должен иметь расширительный или компенсационный бачок, соединенный с одним из сечений трубопровода, чаще всего с сечением у входа в насос, где давление имеет минимальное значение. Без этого бачка абсолютное давление внутри замкнутого трубопровода было бы неопределенным и переменным в связи с колебаниями температуры и утечками через неплотности.

При наличии расширительного бачка, присоединенного к трубопроводу, как показано на рис. 1.100б давление перед входом в насос

По величине Р₁ можно подсчитать давление в любом сечении замкнутого трубопровода. Если давление в бачке Р₀ изменить на некоторую величину, то во всех точках данной системы давление изменится на ту же самую величину.

Бачок можно включить также в замкнутый трубопровод, как показано на рис. 1.100б штриховой линией (трубопровод внутри бачка при этом должен иметь разрыв).

Видео:Семинар. Уравнение баланса напоров для участка магистрального нефтепроводаСкачать

Проектирование и эксплуатация магистральных нефтепроводов (стр. 10 )

Уравнение баланса напоров для трубопровода

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13

K З – коэффициент загрузки электродвигателя, равный отношению мощности на валу электродвигателя N в к его номинальной мощности N эл. ном :

. (5.45)

Значения коэффициентов в формуле (5.45)

Потребляема мощность для НПС с РП, с учётом (5.37), определиться как

. (5.46)

5.3.2 Уравнение баланса напоров

Рассмотрим работу одной ГНПС на МН: с одной стороны потребный напор для ведения перекачки с расходом Q определён ранее уравнением (5.11), с другой стороны располагаемый напор в начальном сечении трубопровода определяется уравнением (5.40), тогда приравняв располагаемый напор к потребному получим уравнение баланса напоров

, (5.47)

где h ост = p К /( r × g ) – остаточный напор в конце МН, м. Переход от давления к остаточному напору удобен потому, что последний определяется уровнем взлива в резервуаре, его нивелирной отметкой и потерями в подводящих трубопроводах. Ориентировочно можно принять h ост =30–40 м [2, 3, 25–27].

Левая часть уравнения (3.45) – это суммарный напор, развиваемый подпорной и магистральной насосными (располагаемый напор), а правая – напор, необходимый для ведения перекачки с проектным расходом Q (потребный напор) . Уравнение баланса напоров показывает, что расход в трубопроводе устанавливается сам собой (автоматически) таким образом, чтобы суммарный напор, развиваемый всеми работающими насосами, был равен напору, необходимому для ведения перекачки.

Графической интерпретацией уравнения баланса напоров является совмещенная характеристика нефтепровода и нефтеперекачивающих станций. На рис. 5.11 кривая МН изображает характеристику трубопровода, а кривая НПС – суммарную напорную характеристику всех работающих насосов. Точка пересечения характеристик называется рабочей точкой (Р), которая определяет пьезометрический напор в начале нефтепровода H Р и его производительность Q Р нефтепровода при заданных условиях перекачки. В левой части рис. 5.11 показано распределение напоров по ЛЧ МН.

Так как в правой части уравнения (5.47) расход подставляют в м3/с, то и в левой части уравнения необходимо перейти к этой же размерности, для этого замени коэффициент b в уравнении (5.35)–(5.39) на , а Q ч (м3/ч) на Q (м3/с).

Рис. 5.11. Графическая интерпретация уравнения баланса напоров

5.3.3 Особенности технологического расчёта МН с промежуточными перекачивающими станциями

Большая часть МН имеет промежуточные НПС. При этом возможны две основные схемы перекачки: «из насоса в насос» и «с подключенными резервуарами» (преимущества и недостатки указанных схем перекачки рассматривались в п.1.2.2). Рассмотрим уравнение баланса напоров для МН с тремя НПС, две из которых промежуточные НПС без РП (см. рис. 5.12). Если по трассе отсутствуют сбросы и подкачки, то можно составит следующую систему, записав уравнения баланса напоров для каждого перегона.

(5.48)

Здесь напор, создаваемый каждой НПС записан формулой (5.37) с заменой на =, остальные величины приводятся на рис. 5.12.

В системе уравнений (5.48) три неизвестных: расход Q и подпоры перед промежуточными НПС h П 2 и h П 3 . Сложив почленно все уравнения системы (5.48) получим уравнение баланса напоров для всего трубопровода

, (5.49)

Как можно увидеть в правой части находится суммарный напор создаваемый включенными магистральными насосами всех НПС и подпорными насосами первой станции, а левая часть представляет собой гидравлические потери во всём МН, т. е. для определения расхода можно считать, что все насосы расположены на первой НПС (см. рис. 5.12). Графическая интерпретация уравнения (5.49) приводится на рис. 5.12а, на рис. 5.12б показано распределение реальных напоров (сплошными линиями) и мнимых напоров (тонкой пунктирной линией).

Равенство создаваемого и требуемого напоров, а также равенство подачи насосов и расхода нефти в трубопроводе приводят к важному выводу: трубопровод и все НПС в пределах эксплуатационного участка составляют единую гидравлическую систему. Изменение режимов работы НПС (отключение части насосов или НПС) приведет к изменению режима МН в целом. Изменение гидравлического сопротивления трубопровода или отдельного его перегона (изменение вязкости, включение резервных ниток, замена труб на отдельных участках трассы и т. п.), в свою очередь, окажет влияние на режим работы всех НПС.

Рис. 5.12. Схема нефтепровода с промежуточными НПС

Зная производительность Q при данной схеме включения можно определить подпоры перед промежуточными НПС. Для определения подпора перед с-й НПС необходимо сложить с первых уравнений системы (5.48), тогда в общем виде получим

. (5.50)

Напор на выходе с-й НПС получим, сложив следующие величины

, (5.51)

Для работы МН необходимо выполнение следующих условий:

; (5.52)

, (5.53)

, (5.54)

где h min i , Hmax i , – соответственно разрешенные значения минимального напора на входе, максимального напора на выходе и максимального напор в нагнетательном коллекторе i -й НПС.

Если не выполняется условие (5.52) и (5.53), то срабатывает система автоматического регулирования (САР) НПС, при этом подпор перед НПС и напор в коллекторе увеличиваются, а напор после НПС уменьшается. Если не выполняется условие (5.54), то часть насосов должна быть выключена.

Уравнение баланса напоров для МН с N Э эксплуатационными участками можно получить, рассуждая аналогично, при этом вместо h п появится напор N Э × h п , а вместо h ост – напор N Э × h ост , после чего уравнение (5.49) примет вид

. (5.55)

Как правило, режимы работы МН рассчитывают по отдельным эксплуатационным участкам. Кроме того, при остановке одного эксплуатационного участка, другие некоторое время будут работать на имеющемся запасе нефти, что повышает надёжность МН.

5.3.4 Решение уравнения баланса напоров

Уравнение баланса напоров позволяет определять производительность – расход, устанавливающийся в трубопроводе, и распределение напоров по ЛЧ. Для решения уравнения баланса напоров относительно расхода перекачки можно использовать следующие методы:

1. Графо-аналитический метод – является наиболее наглядным и, хотя достаточно трудоёмок, позволяет относительно просто решать достаточно сложные задачи (например, определить расходы в ветвях сложного разветвлённого нефтепровода). Для его реализации проводится расчёт суммарного потребного напора всего нефтепровода и суммарного напора, создаваемого насосами НПС, для нескольких значений расходов (подач). Результаты расчётов наносятся на плоскость Q – H и соединяются плавными линиями. Точка пересечения суммарных кривых указывает суммарный расход в МН и пьезометрический напор в его начале, либо суммарный напор, создаваемый всеми НПС. Далее по правилам построения гидравлических характеристик соединений простых трубопроводов определяются расходы в соответствующих ветвях (см. рис. 5.13).

Рис. 5.13. Графоаналитическое решение уравнения баланса напоров

2. Метод последовательных приближений, для реализации которого выразим потери на трение через расход, применяя уравнение Дарси-Вейсбаха, тогда получим следующее трансцендентное уравнение

, (5.56)

где n и m – число параллельно включенных работающих подпорных насосов и число последовательно включенных работающих магистральных насосов.

Выразим из уравнения (5.56) расход

, (5.57)

Ход решения уравнения (5.57) аналогичен решению уравнения (5.12) и приводится в п. 5.2.3.

3. Аналитическое решение (для заданного гидравлического режима) уравнения баланса напоров можно получить, представив зависимость напора, развиваемого насосами, от расхода в следующем виде

, (5.58)

где коэффициенты A и B определяются при обработке экспериментальных данных или из решения системы уравнений

(5.59)

Решая относительно коэффициентов A и B , получим:

; (5.60)

. (5.61)

В качестве Q 1 и Q 2 , согласно [18, 27] принимаем: Q 1 =0,8 · Q ном .; Q 2 =1,2 · Q ном , однако если рабочая точка системы выйдет за пределы рабочей зоны эти значения необходимо будет откорректировать.

Нетрудно заметить, что для зоны смешанного трения коэффициенты A и B будут приблизительно равны, а для зоны квадратичного трения строго равны коэффициентам паспортной характеристики a и b .

Тогда уравнение (5.49) можно записать в виде

.(5.62)

Решая уравнение (5.62) относительно расхода, получим

. (5.63)

Порядок определения расхода по уравнению (5.63) аналогичен решению уравнения (5.13), которое рассмотрено в п. 5.2.3.

Решение указанным способом достаточно трудоёмко, однако позволяет решать в аналитическом виде большинство задач трубопроводного транспорта.

4. Численное решение может быть организовано различными методами, наиболее простой из них это подбор параметра, который можно реализовать при помощи встроенной функции «подбор параметра» в Microsoft Exel .

5.4.1 Изменение пропускной способности МН в процессе эксплуатации

Изменение пропускной способности МН в течении времени связано:

— с изменением реологических параметров нефти вследствие сезонного изменения температуры, а также влиянием содержания воды, парафина, растворенного газа и т. п.;

— с уменьшением несущей способности секций труб при эксплуатации;

— с засорением внутренней полости трубопровода;

Температура нефтей и нефтепродуктов, при транспорте и хранении, изменяется в течении года, что ведёт к изменению пропускной способности МН. Минимальную пропускную способность трубопровод имеет в марте–апреле, когда температура грунта и перекачиваемой нефти наименьшая. С повышением температуры в весеннее–летний период пропускная способность увеличивается и достигает максимального значения в августе. Практикой установлено, что пропускная способность МН в тёплое время года возрастает до 110–114 % от расчётной (проектной) пропускной способности в зимнее время.

Для того чтобы определить во сколько раз изменится пропускная способность МН (при неизменном давлении) при изменении коэффициента кинематической вязкости с n до n Н , обусловленную сезонным колебанием температур, разделим новую пропускную способность Q Н , определённую по (5.10) на старую Q

. (5.64)

С течением времени, за счёт коррозии и других процессов, способствующих уменьшению толщины стенки трубопровода и появлению других дефектов, несущая способность секций трубопровода уменьшается, что ведёт к необходимости понижать давления на выходе НПС, а, следовательно, к изменению гидравлического уклона МН. Влияние несущей способности на пропускную способность можно выразить через гидравлические уклоны

. (5.65)

В процессе эксплуатации внутренняя полость труб нефтепровода засоряется скоплением воды, парафина, паров, механических примесей. Постепенное нарастание этих скоплений приводит к росту гидравлического сопротивления трубопровода, что неминуемо скажется на пропускной способности последнего. Оценка состояния внутренней полости производится по величине эффективного диаметра D ЭФ или по величине коэффициента гидравлической эффективности участка МН Е.

Эффективный диаметр показывает, каким должен быть диаметр простого трубопровода, чтобы его гидравлический уклон равнялся фактическому уклону участка и определяется из уравнения (5.10) c учётом фактического гидравлического уклона МН

, (5.66)

где i Ф – фактическая величина гидравлического уклона, которая выражается из уравнения (5.3) по существующим давлениям в начале и конце рассматриваемого участка

, (5.67)

Эффективность работы является более информативной величиной, так как показывает не только наличие загрязнения, но и дает оценку их влияния на гидравлическое сопротивление участка и оценивается соотношением теоретического и фактического гидравлических уклонов:

. (5.68)

Тогда влияние состояния внутренней полости на пропускную способность МН можно оценить следующими зависимостями

. (5.69)

. (5.70)

5.4.2 Практика изменения режимов перекачки

Системы МН предназначены для перекачки больших объемов нефти от поставщиков к многочисленным потребителям, находящимся как внутри, так и за рубежами страны. Управление процессами перекачки для таких систем подчинено жесткому требованию [28]: оно должно обеспечивать выполнение планов приема нефти от поставщиков и сдачи нефти по всем потребителям системы за некоторый плановый период времени. Управление собственно процессом перекачки сводится к выбору и выполнению определенных режимов работы МН.

Ни один МН не работает с постоянной производительностью в течение расчетного числа суток перекачки. Это связано с целым рядом причин:

— изменение со временем пропускной способности (см. п.5.4.1);

— пуск очистных устройств;

— отказы основного оборудования;

— неритмичность и перебои в поставках плановых объемов нефти;

— неравномерность приема плановых объемов нефти нефтеперерабатывающими заводами;

— отсутствие нефти в резервуарах ГНПС (головных ННПС эксплуатационных участков), или недостаточное по сравнению с плановым поступление нефти в эти резервуары, отсутствие свободного объема в резервуарах КП;

— переменная загрузка МН, которая обусловлена различной закономерностью работы поставщиков нефти, нефтепровода и потребителей (НПЗ).

5.4.3 Классификация методов регулирования

С учётом (5.39) и (5.33) уравнение баланса напоров (5.47) можно представить в виде следующей системы уравнений

(5.71)

Из уравнения (5.71) следует, что все методы регулирования можно условно разделить на две группы: методы, связанные с изменением параметров НПС и методы, связанные с изменением параметров трубопровода. С другой стороны все методы можно разделить на методы «дискретного» и «плавного» регулирования. Для методов «плавного» регулирования характерно изменение технологических параметров в широком диапазоне, а для методов «дискретного» регулирования характерно скачкообразное изменение технологических параметров.

Разделение методов регулирования технологических параметров по указанным критериям представлено в табл. 5.5.

Классификация методов регулирования

Группа методов, направленная

на изменение параметров НПС

Группа методов, направленная

на изменение параметров ЛЧ

— использование сменных роторов

— обточка рабочих колёс насосов1

— изменение схемы включения насосов

изменение схемы включения ЛЧ

— изменение частоты вращения вала насоса

применение противотурбулентных присадок

1. Метод позволяет производить «плавное» регулирование технологических параметров НПС, но количество и объёмы обточек ограничены, в тоже время метод не позволяет обеспечивать плавное регулирование в процессе эксплуатации

2. Методы можно отнести к группе, направленной на изменение параметров ЛЧ, однако эти изменения касаются гидравлических характеристик трубопроводов НПС, а следовательно и суммарной характеристик НПС

5.4.4 Дискретное регулирование характеристик НПС

Большинство современных магистральных насосов укомплектовано сменными роторами на подачу 0,5· Q Н , 0,7· Q Н и 1,25· Q Н , которые имеют различные характеристики (рис. 5.14). Установка сменных роторов позволяет произвести дискретное изменение напора для каждого магистрального (на 20–30 м) и расхода в МН см рис. 5.14.