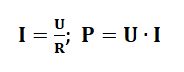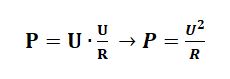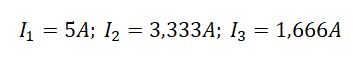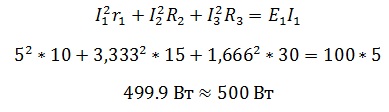Уравнение баланса мощности цепи постоянного тока алгебраическая сумма мощностей всех

Видео:Работа и мощность электрического тока. Баланс мощностей в электрической цепи. КПД электрической цепиСкачать

Баланс мощностей

Содержание:

Баланс мощностей

Для любой электрической цепи суммарная мощность , развиваемая источниками электрической энергии (источниками тока и ЭДС), равна суммарной мощности , расходуемой потребителями (резисторами):

Мощность, рассеиваемая резистором, , мощность источника ЭДС , мощность источника тока .

Мощности, рассеиваемые резисторами, всегда положительные, в то время как мощности источников электрической энергии, в зависимости от соотношения направления падений напряжения и тока в них, могут иметь любой знак. Мощность положительна, когда направление тока через источник тока противоположно падению напряжения на нем. Он питает электрическую цепь. В противном случае источник питания является отрицательным, и вы являетесь потребителем электрической энергии. Следует заметить, что направление падения напряжения всегда противоположно направлению ЭДС, поэтому для источника ЭДС условием положительной мощности является совпадение направлений ЭДС и тока.

Пример расчёта разветвлённой цепи постоянного тока

Рассмотрим решение задачи для цепи, представленной на рис. 1.6, описанными выше методами расчёта.

Дано

1) все неизвестные токи, используя законы Кирхгофа; показать, что баланс мощностей имеет место;

1) Применение законов Кирхгофа. Баланс мощностей.

Всего в схеме семь ветвей =7, ветвей с источниками тока = 1, число неизвестных токов равно , количество узлов — , число уравнений по первому закону Кирхгофа , число уравнений по второму закону Кирхгофа —

Возможно вам будут полезны данные страницы:

Выберем положительные направления токов и обозначим их стрелками. Выберем и обозначим стрелками направления обхода трёх независимых контуров: Составим систему уравнений по законам Кирхгофа

для узла а ;

для узла b

для узла с или ;

для контура ,

для контура

для контура

Полученные уравнения после подстановки в них числовых значений будут иметь следующий вид:

Решение данной системы:

Баланс мощностей для рассматриваемой цепи

Получено тождество 252 Вт = 252 Вт.

Примечание: падение напряжения на источнике тока определено по второму закону Кирхгофа для контура, содержащего и , как

Баланс мощностей

В любой электрической цепи должен соблюдаться энергетический баланс -баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

В левой части равенства слагаемое берется со знаком «+» если Е и I совпадают по направлению и со знаком если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Баланс мощностейСкачать

Баланс мощностей электрической цепи

Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.

Видео:Баланс мощностей | Активная мощностьСкачать

Определение

Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.

Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.

Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:

Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.

Видео:Баланс мощностей цепи переменного тока│Активная, реактивная и полная мощностиСкачать

Назначение

Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.

Видео:#П.4 Уравнение баланса мощностей / мощность потребителя / мощность генератораСкачать

Переменный ток

Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.

1. Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
2. Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
3. Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.

Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.

Видео:Проверка решений балансом мощностей | Теоретическим основам электротехникиСкачать

Постоянный ток

В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.

1. В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
2. I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
3. Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
4. Pист=I×E=1×10=10 Ватт. Это значение для источника.
5. Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
6. Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.

При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Заключение

В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.

Видео:Мощность в цепях синусоидального тока. Баланс мощностейСкачать

Видео по теме

Видео:8 класс, 21 урок, Расчет электрических цепейСкачать

Мощность в цепи постоянного тока

Здравствуйте! Эту статью можно считать началом знакомства с электричеством. Напряжение, ток, сопротивление – это три главные величины, на которых построены основные законы электротехники и эти величины связаны между собой еще одной – мощностью. А чтобы было проще знакомиться с электротехникой, мы будем рассматривать мощность в цепи постоянного тока. Дело в том, что при расчетах в цепях переменного тока появляется довольно много условий. Впрочем, обо всём по порядку и вы сейчас сами с этим разберётесь.

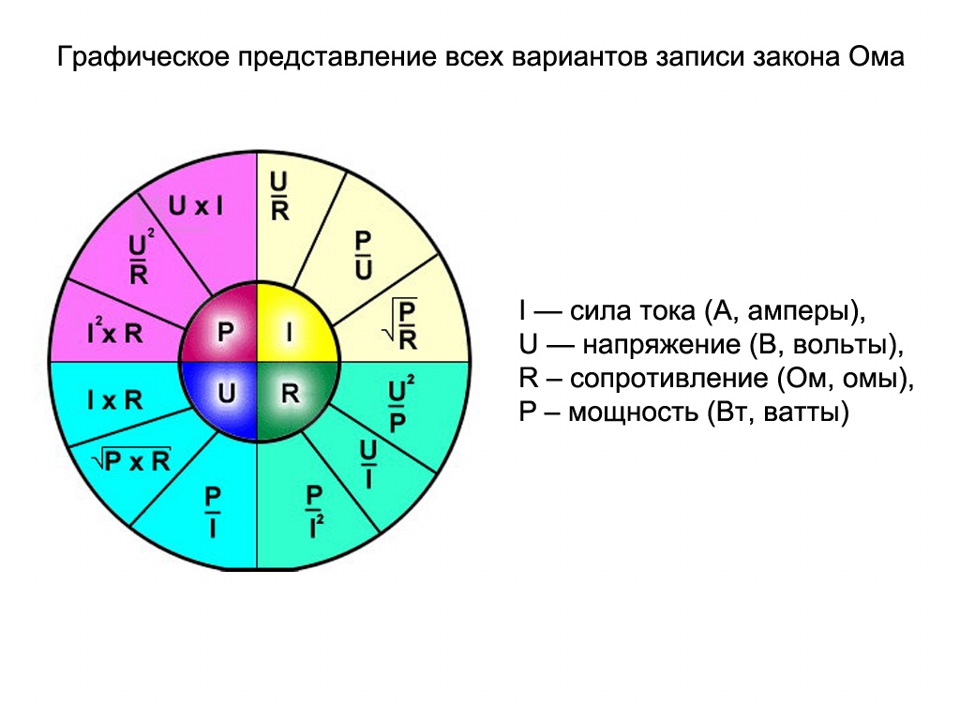
Для удобства я сразу напишу международные обозначения этих четырёх величин:

U – напряжение (В, вольт)

R – сопротивление (Ом, ом)

P – мощность (Вт, ватт – не надо путать с вольтом, который обозначается только одной буквой В)

Для начала абстрактный пример, чтобы проще было понимать термины, которые я сейчас буду использовать. Допустим, есть магазин товаров (условно это можно представить, как напряжение), есть деньги (условно это будет ток), есть совесть, которая не позволяет вам тратить много или наоборот, шепчет, чтобы вы крупно потратились (это можно считать сопротивлением) и есть купленные товары или продукты, которые вы несёте домой (это мощность). Собственно, на этом примере можно объяснить многие законы, связанные с электрическим током. Все обозначенные величины связаны между собой законом Ома, который гласит, что сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению цепи, а именно:

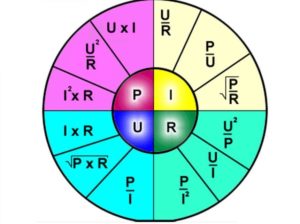
В абстрактном примере – чем больше магазин (напряжение) и чем меньше вам шепчет совесть (сопротивление), тем больше вы тратите денег (сила тока), а когда вы несёте купленный товар домой, вы совершаете работу (мощность). Мощность в цепи постоянного тока это и есть работа, совершаемая электричеством. Мощность это произведение тока на напряжение, а если вместо тока или напряжения подставить соответствующие значения, то можно получить мнемоническую табличку:

Как видите, мощность в цепи постоянного тока это довольно простое понятие, если немного вдуматься в материал. По сути, это всего две формулы с заменой значений. Как это выглядит:

Если теперь в формуле мощности подставить место значения тока формулу тока, то получим следующее:

Именно таким образом и получилось 12 формул на основе закона Ома, которые вы видите в мнемонической табличке. Что такое мощность в цепях постоянного тока мы более или менее разобрались, но есть ещё один момент.

Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Баланс мощностей в цепи постоянного тока.

Собственно, это просто проверка правильности расчетов электрической цепи. Возвращаясь к нашему абстрактному примеру это выглядит так: вы купили товары, забрали их на кассе, отошли от кассы и вам показалось, что ваши пакеты должны быть больше или меньше, чем получились. Тогда вы берёте чек и начинаете сравнивать товар в чеке и товар в наличии. Если товары в чеке и товары в руках совпали, значит всё в порядке. Если мы обратимся к определению, то баланс мощностей – сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками.

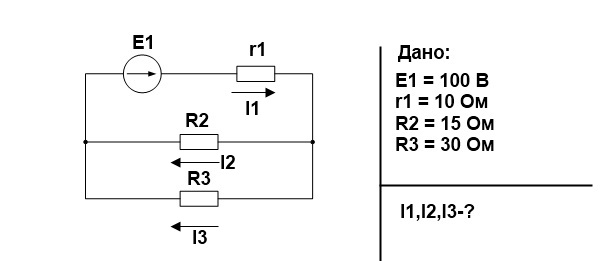
Как это использовать на практике? Допустим, у нас есть задача, которую нужно решить:

Поскольку решение задачи не является целью этой статьи, я дам уже готовые ответы.

Теперь надо проверить правильно ли были посчитаны токи в задаче. Ток в цепи равен току , следовательно, мощность источника питания (Е1хI1) должна быть равна сумме мощностей сопротивлений

Что мы и получаем с учетом потерь при округлениях.

Таким образом, баланс мощностей в электрической цепи постоянного тока — это ничто иное, как проверка самого себя, своих расчётов.

Как видите, мощность в цепи постоянного тока посчитать довольно легко. Гораздо больше сложностей возникнет, если ток будет переменный. Другими словами, на примере магазина это выглядит так:

Постоянный ток – от входа до выхода прямая линия и вы спокойно идете от начала и до конца без каких-либо приключений.

Переменный ток – магазин представляет из себя зигзаг и вам приходится делать лишние движения.

Поэтому в переменном токе мощность считать немного сложнее, но это уже тема совсем другой статьи.

📺 Видео

Баланс мощностей. Пример 1Скачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Мощность в цепи переменного тока. 11 класс.Скачать

Метод контурных токов - определение токов. ЭлектротехникаСкачать

Урок 363. Мощность в цепи переменного токаСкачать

2 7 Методы расчета цепей постоянного токаСкачать

Лекция 020-6. Мощность в цепях постоянного тока. Баланс мощностиСкачать

Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать

Электричество за 2 минуты! Напряжение, сила, мощность, постоянный и переменный ток. ПРОСТО О СЛОЖНОМСкачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать