Комплексной мощностью 
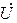
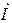
Знак мнимой части сопряжённого комплекса изменён на обратный ( 




Пусть на участке электрической цепи известно напряжение 


Тогда полная комплексная мощность 

где 


Знак «+» перед 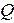
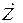
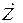
При выполнении условия баланса мощностей активная и реактивная мощности источников питания должны равняться потребляемым активной и реактивной мощностям.
Мощности источника Э.Д.С. определяем по формуле:

где 
Мощность источника тока:

где 

Мощность источника Э.Д.С. входит в выражение баланса со знаком «+», если направление Э.Д.С. источника и тока в этой ветви совпадают; если направления Э.Д.С. источника и тока не совпадают, то мощность источника Э.Д.С. отрицательная.
Мощность источника тока входит в выражение баланса со знаком «+», если ток источника и напряжения на его зажимах направлены навстречу друг другу. При совпадении направлений тока источника и напряжения мощность источника отрицательная.
Активная и реактивная мощности потребителей равны соответственно:

где 

где 
При выполнении условия баланса мощностей:


Примеры расчёта цепей однофазного синусоидального тока
Пример 6.1
 | Дано:  , ,  , ,  , , 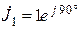 Определить токи в ветвях, составить и рассчитать баланс мощностей для схемы на рис. 6.1. Определить токи в ветвях, составить и рассчитать баланс мощностей для схемы на рис. 6.1. |
| Рис. 6.1 |
Решение
Для расчёта будем использовать метод контурных токов.
Значение контурного тока 



Выражаем ток 

Ток в третьей ветви равен контурному току 


Ток во второй ветви определим как алгебраическую сумму контурных токов, проходящих через данную ветвь:

Полная мощность приёмников определяется по формуле:

Активную мощность приёмников в данной схеме определим по следующей формуле:


Реактивную мощность приёмников определяем по формуле:

Полная мощность, выделяемая в систему источниками, определяется по формуле:
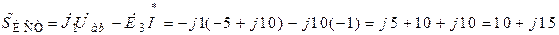



Выполнение баланса мощностей подтверждает правильность решения задачи.
Ответ: 

Пример 6.2
 Рис. 6.2 Рис. 6.2 | Дано:  , , 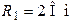 , , 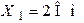 , ,  , , 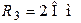 , , 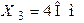 . Для схемы на рис. 6.2 рассчитать ток . Для схемы на рис. 6.2 рассчитать ток  в неразветвлённой части схемы. Записать в неразветвлённой части схемы. Записать 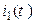 . . |
Решение
Записываем функцию времени 

Определяем входное сопротивление схемы относительно зажимов источника напряжения:


Мгновенное значение тока 

Ответ: 
Пример 6.3
Рассчитать токи 
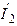
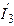
Решение
Графоаналитический метод расчёта – это совокупность графического метода и метода пропорционального пересчёта. Метод основан на линейной зависимости между токами и напряжениями. Поэтому векторная диаграмма напряжений и токов, рассчитанная и построенная для одного значения, питающего цепь напряжения, сохранит свой вид при изменении величины этого напряжения. На диаграмме изменятся лишь масштабы напряжений и токов.
 | Обозначим токи на схеме. Выберем масштабы: масштаб для тока  ; масштаб для напряжения ; масштаб для напряжения  . Построение начинаем из точки, соответствующей отрицательной полярности входных зажимов, это точка «е» (рис. 6.3). . Построение начинаем из точки, соответствующей отрицательной полярности входных зажимов, это точка «е» (рис. 6.3). |
| Рис. 6.3 |
Принимаем действующее значение тока 

 |
| Рис. 6.4 |
Токи и напряжения, определённые с помощью диаграммы, будем обозначать одним штрихом.
Определяем по законуОма для действующих значений напряжения на участках « 



Строим вектора данных напряжений. Участок « 


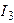
Сумма векторов 





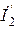


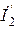

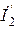










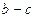



Теперь соединим начало координат (точку «е») с точкой «а», получим вектор приложенного к цепи напряжения 

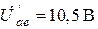

По условию задачи 6.2. действующее значение входного напряжения равно 

Определим исходные токи:



Мгновенные значения этих токов:



Аналогично определяют напряжения на участках цепи.
Построенная в такой последовательности векторная диаграмма напряжений носит название топографической.
Следует помнить!
1) Построение топографической диаграммы начинается из точки, наиболее удалённой от входных зажимов и соответствующей отрицательной полярности источника. Эта точка является базисной, её потенциал условно равен нулю, её помещают в начало координат.
2) Построение векторов напряжений производят навстречу токам. Длина вектора равна его действующему значению, угол между вектором и осью абсцисс равен начальной фазе напряжения.
3) Построение векторов напряжений производят строго в соответствии с расположением элементов в цепи.
4) Каждой точке схемы соответствует определённая точка на топографической диаграмме. Топографические диаграммы представляют диаграммы комплексных потенциалов.
5) Конец вектора напряжения на топографической диаграмме указывает точку высшего потенциала.
Топографическая диаграмма позволяет измерить величину и начальную фазу напряжения любого участка цепи, не участвующего в расчёте. Например, действующее значение между точками « 
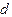

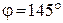
Следовательно 
Пример 6.4
 | Дано:  , ,  , ,  . Определить токи . Определить токи  , , 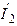 , , 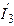 в схеме рис. 6.5; записать их мгновенные значения; определить показания ваттметра; построить векторную диаграмму токов и напряжений. По векторной диаграмме определить показания вольтметра. Проверить выполнение баланса мощностей. в схеме рис. 6.5; записать их мгновенные значения; определить показания ваттметра; построить векторную диаграмму токов и напряжений. По векторной диаграмме определить показания вольтметра. Проверить выполнение баланса мощностей. |
| Рис. 6.5 |
Решение
Применим метод комплексных амплитуд. Изобразим расчетную схему без подключенных приборов (рис. 6.6).
 |
| Рис. 6.6 |
еделим комплексное сопротивление цепи:

Запишем комплекс действующего значения входного нпряжения: 
По закону Ома определяем входной ток:

Для определения токов 
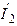

т.к. 

Токи 
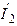

. 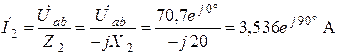
Определим показания ваттметра:

Расчет подтверждает – что активная мощность в ветви с конденсатором отсутствует.
Замечание! При расчете показаний ваттметра положительные направления тока 




Векторную диаграмму токов строим согласно первого закона Кирхгофа в комплексной форме 





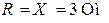

 |
| Рис. 6.7 |
Строим вектора напряжений на всех участках цепи. Построение начинаем из начала координат с вектора напряжения 










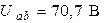
Из конца вектора 



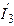

Длина результирующего вектора 


Составим уравнение баланса мощностей в комплексной форме и проверим его выполнение:



Активная мощность потребителей:

Реактивная мощность потребителей:
Баланс мощностей выполняется.
Ответ: 





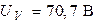
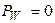
Пример 6.5
 | Дано:  , ,  , ,  , , 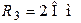 , ,  , ,  , , 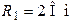 , ,  . Для схемы на рис. 6.8 определить напряжение . Для схемы на рис. 6.8 определить напряжение  и записать его мгновенное значение. и записать его мгновенное значение. |
| Рис. 6.8 |
Решение
Принимаем 1-ый узел за базисный: 
Потенциалы 2–го и 4–го узлов будут соответственно равны:


Составляем уравнение для 3–го узла:

Подставим в уравнение численные значения:




Решив последнее равенство, получим:


Запишем мгновенное значение напряжения:

Ответ: 

Видео:Баланс мощностей | Активная мощностьСкачать

Баланс мощностей электрической цепи
Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.
Видео:Баланс мощностей цепи переменного тока│Активная, реактивная и полная мощностиСкачать

Определение
Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.
Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.
Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:
Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.
Видео:Баланс мощностейСкачать

Назначение
Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.
Видео:Конденсатор в цепи переменного токаСкачать

Переменный ток
Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.
- Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
- Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
- Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.
Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.
Видео:Отличие переменного и постоянного тока наглядно.Скачать

Постоянный ток
В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.
- В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
- I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
- Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
- Pист=I×E=1×10=10 Ватт. Это значение для источника.
- Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
- Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.
При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.
Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Заключение
В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.
Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Видео по теме
Видео:Переменный токСкачать

Баланс мощностей
Содержание:
Баланс мощностей
Для любой электрической цепи суммарная мощность 

Мощность, рассеиваемая резистором, 


Мощности, рассеиваемые резисторами, всегда положительные, в то время как мощности источников электрической энергии, в зависимости от соотношения направления падений напряжения и тока в них, могут иметь любой знак. Мощность положительна, когда направление тока через источник тока противоположно падению напряжения на нем. Он питает электрическую цепь. В противном случае источник питания является отрицательным, и вы являетесь потребителем электрической энергии. Следует заметить, что направление падения напряжения всегда противоположно направлению ЭДС, поэтому для источника ЭДС условием положительной мощности является совпадение направлений ЭДС и тока.
Пример расчёта разветвлённой цепи постоянного тока
Рассмотрим решение задачи для цепи, представленной на рис. 1.6, описанными выше методами расчёта.

1) все неизвестные токи, используя законы Кирхгофа; показать, что баланс мощностей имеет место;
1) Применение законов Кирхгофа. Баланс мощностей.
Всего в схеме семь ветвей 




Возможно вам будут полезны данные страницы:
Выберем положительные направления токов и обозначим их стрелками. Выберем и обозначим стрелками направления обхода трёх независимых контуров: 
для узла а 
для узла b
для узла с 

для контура 
для контура 
для контура 
Полученные уравнения после подстановки в них числовых значений будут иметь следующий вид:

Баланс мощностей для рассматриваемой цепи
Получено тождество 252 Вт = 252 Вт.
Примечание: падение напряжения на источнике тока 


Баланс мощностей
В любой электрической цепи должен соблюдаться энергетический баланс -баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.
В левой части равенства слагаемое берется со знаком «+» если Е и I совпадают по направлению и со знаком 
Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.
На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Услуги:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
🔍 Видео
Как переменный ток идет через конденсатор? #энерголикбез за пару минут!Скачать

Реактивная мощность за 5 минут простыми словами. Четкий #энерголикбезСкачать

Электричество за 2 минуты! Напряжение, сила, мощность, постоянный и переменный ток. ПРОСТО О СЛОЖНОМСкачать

Мощность в цепи переменного тока. 11 класс.Скачать

Мощность в цепях синусоидального тока. Баланс мощностейСкачать

Резистор в цепи переменного(синусоидального) токаСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

3 7 Баланс мощностей в цепи переменного синусоидального токаСкачать

Баланс мощностей. Пример 1Скачать

Урок 363. Мощность в цепи переменного токаСкачать

ПЕРЕМЕННЫЙ ТОК │ Основные понятия и определения │Мощность. Теория ч.1Скачать























