Уравнение баланса мощностей в интегральной форме (4 видео)

Уравнение баланса мгновенных значений мощности

Как уже отмечалось в 1.1, электромагнитное поле является одной из форм материи. Как и любая другая форма материи, оно обладает энергией. Эта энергия может распространяться в пространстве и преобразовываться в другие формы энергии.

Сформулируем уравнение баланса для мгновенных значений мощности применительно к некоторому объему V, ограниченному поверхностью S (рис. 1.23). Пусть в объеме V, заполненном однородной изотропной средой, находятся сторонние источники. Из общих физических представлений очевидно, что мощность, выделяемая сторонними источниками, может расходоваться на джоулевы потери и на изменение энергии электромагнитного поля внутри V, а также может частично рассеиваться, уходя в окружающее пространство через поверхность S. При этом должно выполняться равенство

, (1.120)

где Рст – мощность сторонних источников;

Рп – мощность джоулевых потерь внутри объема V;

– мощность, проходящая через поверхность S;

W– энергия электромагнитного поля, сосредоточенного в объеме V, adW/dt– мощность, расходуемая на изменение энергии в объеме V.

Рис. 1.23. Объем V, ограниченный поверхностью S

В данном разделе будут использованы уравнения состояния (1.53). Эти уравнения не позволяют учесть потери энергии при поляризации и намагничивании среды. Поэтому слагаемое Рпв равенстве (1.120) фактически определяет мощность джоулевых потерь в объеме V, обусловленных током проводимости.

Уравнение (1.120) дает только качественное представление об энергетических соотношениях. Чтобы получить количественные соотношения, нужно воспользоваться уравнениями Максвелла. Рассмотрим первое уравнение Максвелла с учетом сторонних токов (1.111). Все члены этого уравнения – векторные величины, имеющие размерность А/м2.

Чтобы получить уравнение, аналогичное (1.120), нужно видоизменить первое уравнение Максвелла (1.111) так, чтобы его члены стали скалярными величинами, измеряющимися в ваттах. Для этого достаточно все члены указанного равенства скалярно умножить на вектор Е, а затем проинтегрировать полученное выражение по объему V. После скалярного умножения на вектор Е получаем

(1.121)

Используя известную из векторного анализа формулу div[E,H]= Н rot Е – Е rot H, преобразуем левую часть соотношения (1.121) и заменим rot E его значением из второго уравнения Максвелла (1.39):

Подставляя это выражение в (1.121), получаем

(1.122)

В последнем слагаемом в правой части (1.122) изменен порядок сомножителей в скалярном произведении векторов и Н. Это допустимо, так как . Данное изменение не является принципиальным и не дает никаких преимуществ при выводе рассматриваемого здесь уравнения баланса для мгновенных значений мощности. Однако при такой записи во всех членах уравнения (1.122) второй сомножитель (векторы jст, j, и Н) является вектором, входившим ранее в первое уравнение Максвелла. Это обстоятельство позволит в дальнейшем (см. 1.8.4) несколько упростить вывод уравнения баланса в случае монохроматического поля (уравнения баланса комплексной мощности). Интегрируя почленно уравнение (1.122) по объему V, получаем

(1.123)

где направление элемента dSсовпадает с направлением внешней нормали к поверхности S. При переходе от (1.122) к (1.123) использована теорема Остроградского – Гаусса для перевода объемного интеграла от div [Е, Н] в поверхностный интеграл от векторного произведения [Е, Н]. Введем обозначение

и преобразуем подынтегральное выражение в последнем слагаемом в правой части (1.123):

(1.125)

Подставляя (1.124) и (1.125) в (1.123) и меняя порядок интегрирования и дифференцирования, получаем

. (1.126)

Выясним физический смысл выражений, входящих в уравнение (1.126).

Рассмотрим первое слагаемое в правой части (1.126). Представим объем Vввиде суммы бесконечно малых цилиндров длиной dl, торцы которых (dS) перпендикулярны направлению тока (вектору j). Тогда EjdV= EjdV= (Edl)(jdS) = dUdl= dPп, где dl=jdS– ток, протекающий по рассматриваемому бесконечно малому цилиндру; dU= Edl– изменение потенциала на длине dl, adPп – мощность джоулевых потерь в объеме dV. Следовательно, рассматриваемое слагаемое представляет собой мощность джоулевых потерь Рп в объеме V. Используя соотношение j = σЕ, для Рп можно получить и другие представления:

(1.127)

Формулы (1.127) можно рассматривать как обобщенный закон Джоуля-Ленца (П. 33), справедливый для проводящего объема Vпроизвольной формы.

Интеграл в левой части (1.126) отличается от первого слагаемого в правой части только тем, что в подынтегральное выражение вместо j входит jст. Поэтому он должен определять мощность сторонних источников. Будем считать положительной мощность, отдаваемую сторонними токами электромагнитному полю. Электрический ток представляет собой упорядоченное движение заряженных частиц. Положительным направлением тока считается направление движения положительных зарядов. Ток отдает энергию электромагнитному полю при торможении образующих его заряженных частиц. Для этого необходимо, чтобы вектор напряженности электрического поля Е имел составляющую, ориентированную противоположно направлению тока, т.е. чтобы скалярное произведение векторов Е и jст было отрицательным (Ejст Будет полезно почитать по теме:

Содержание

Тема 4. баланс энергии ЭМП
Баланс мощностей электрической цепи
Определение
Назначение
Переменный ток
Постоянный ток
Заключение
Видео по теме
💥 Видео

Видео:Баланс мощностейСкачать

Тема 4. баланс энергии ЭМП

Плотность ЭМ энергии и энергия, сосредоточенная в объеме. Мощность тепловых потерь и сторонних источников. Уравнение баланса для мгновенных значений мощности в дифференциальной и интегральной форме (теорема Умова – Пойнтинга). Физическая трактовка. Мощность, выходящая и входящая из объема через замкнутую поверхность. Вектор Пойнтинга. Мощность на входе приемника. Вектор Пойнтинга изотропного источника.

Средние за период значения энергетических характеристик гармонического ЭМП. Теорема Умова – Пойнтинга для комплексных мощностей. Комплексный вектор Пойнтинга. Уравнения баланса для активных и реактивных мощностей. Физическая трактовка. Скорость переноса энергии ЭМП.

Указания к теме

Поскольку ЭМ форма движения материи подчиняется закону сохранения энергии, непосредственно из системы уравнений Максвелла следует уравнение баланса энергии ЭМП (теорема Умова – Пойнтинга).

Необходимо учесть, что источником ЭМП является сторонняя сила, которую поддерживают посторонние по отношению к исследуемому полю источники. Сторонние источники не зависят от исследуемого поля и вводятся в основные уравнения ЭМП в виде дополнительных слагаемых.

При изучении этой темы важно уяснить физическое содержание каждого слагаемого уравнений баланса энергии как для некоторой области, так и для любой точки пространства. Необходимо рассмотреть различные виды балансов энергии (пассивный, нейтральный, активный) на примере LC-контура, чтобы уяснить связь между вектором Пойнтинга и движением энергии, ее излучением или поглощением, притоком или оттоком, скоростью движения энергии.

При изучении гармонических полей нужно обратить внимание на средние за период энергетические характеристики ЭМП, физическое содержание вещественной и мнимой частей вектора Пойнтинга.

Необходимо уяснить связь вектора Пойнтинга с мощностью, принимаемой антенной в дальней зоне приема, а также понять, почему плотность потока энергии изотропного источника убывает при удалении от него даже при отсутствии потерь в пространстве.

Основные сведения

После преобразования уравнений (2.5)–(2.8) [1–6] получаем дифференциальнуюформу теоремы Умова – Пойнтинга

. (4.1)

После интегрирования по объему (4.1) и преобразований получаем

. (4.2)

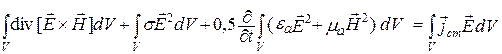
Каждое слагаемое в выражении (4.2) имеет размерность мощности

. (4.3)

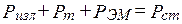
Уравнения (4.2)–(4.3) позволяют сформулировать теорему Умова –Пойнтинга: «Мощность стороннего источника в данном объеме расходуется на излучение, тепловые потери и изменение запаса энергии ЭМП» [1–3].

Мощность тепловых потерь (потерь проводимости) подчиняется закону Дж. Джоуля – Э. Ленца. Изменение запаса энергии имеет размерность мощности :

, (4.4)

Вектор называется вектором Пойнтинга. По теореме Остроградского – Гаусса [1–3] .

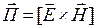
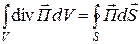
Вектор Пойнтинга указывает направление распространения излучения, а его модуль представляет собой плотность потока мощностиизлучения.

В комплексной форме уравнения (4.2) и (4.3) имеют вид [1]

; (4.5)

, (4.6)

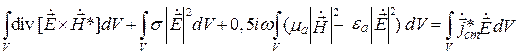
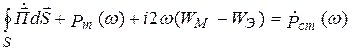
где ; ; ,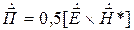

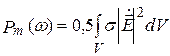
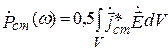
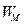
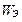
а и – энергия магнитного и электрического полей соответственно.

Выражение (4.6) – баланс комплексных мощностей в объеме V.

Рассмотрим баланс ЭМ энергии (4.3) в контуре, представляющем замкнутую электрическую цепь из элементов с сосредоточенными параметрами (рис. 4.1).

Энергия стороннего источника расходуется на тепловые потери, которые сосредоточены в активном сопротивлении R_т, на изменение запаса ЭМ энергии в контуре (электрическая энергия накапливается в емкости C, а магнитная – в индуктивности L), на излучение из контура (элемент взаимной индуктивности М_ik с другим контуром и «излучающий конденсатор» – электрический вибратор.

Выделим действительную и мнимую части уравнения (4.6)

; (4.7)

. (4.8)

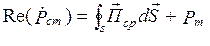
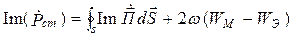
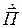
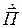
Действительная часть характеризует перенос энергии через граничную поверхность области V в окрестности точки наблюдения, а мнимая часть – колебание энергии через ту же поверхность [1, 12].

Из выражения (4.7) следует, что средняя мощность стороннего источника тратится на тепловые потери в объеме V и на создание ЭМП за пределами V.

Из выражения (4.8) следует, что реактивная мощность стороннего источника расходуется на создание потока реактивной мощности через границу V и на создание запаса реактивной энергии в объеме V. Реактивная мощность характеризует процесс обмена энергией между источником и цепью. При P_р > 0 энергия запасается в магнитном поле, а при P_р

Дата добавления: 2018-09-24 ; просмотров: 2074 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:2.4 Уравнения баланса мощностей в электромагнитном полеСкачать

Баланс мощностей электрической цепи

Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.

Видео:Баланс мощностей | Активная мощностьСкачать

Определение

Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.

Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.

Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:

Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.

Видео:#П.4 Уравнение баланса мощностей / мощность потребителя / мощность генератораСкачать

Назначение

Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.

Видео:Баланс мощностей цепи переменного тока│Активная, реактивная и полная мощностиСкачать

Переменный ток

Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.

Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.

Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.

Видео:Проверка решений балансом мощностей | Теоретическим основам электротехникиСкачать

Постоянный ток

В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.

В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
Pист=I×E=1×10=10 Ватт. Это значение для источника.
Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.

При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.

Видео:3.4 Уравнения баланса мощностей в монохроматическом полеСкачать

Заключение

В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать