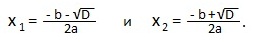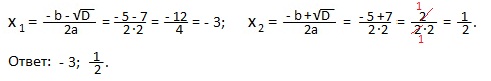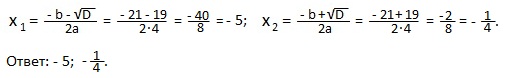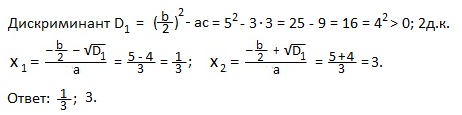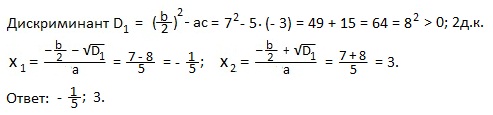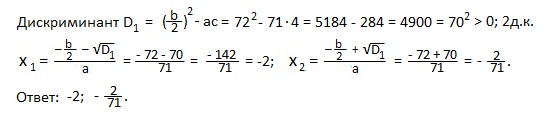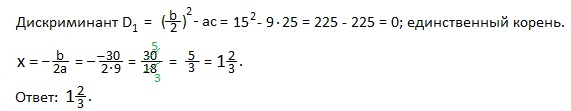Формулы корней квадратных уравнений
Пусть дано квадратное уравнение ax 2 + bx + c = 0 . Преобразуем квадратный трехчлен ax 2 + bx + c методом выделения полного квадрата.
Обычно выражение b 2 — 4ac обозначают буквой D и называют дискриминантом квадратного уравнения ax 2 + bx + c = 0 .
Любое квадратное уравнение можно преобразовать к этому виду, удобному для того, чтобы определять число корней квадратного уравнения и находить эти корни.
Решение: a = 2, b = 4, c = 7
D = 4 * 4 — 4 * 2 * 7 = 16 — 56 = — 40
Так как D , то действительных корней нет.
2. Если D = 0 , то квадратное уравнение имеет один корень, который находится п о формуле:
и это единственный корень уравнения.
4x 2 — 20x + 25 = 0
Решение: a = 4, b = -20, c = 25
D = (-20)* (-20) — 4 * 4 * 25 = 400 — 400 = 0
Так как D = 0 , то данное уравнение имеет один корень:
3. Если D > 0 , то квадратное уравнение имеет два корня:
3x 2 + 8x — 11 = 0
Решение: a = 3, b = 8, c = -11
D = (-8)* (-8) — 4 * 3 * (-11) = 64 + 132 = 196
Так как D > 0 , то имеются два корня уравнения:
Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать
Квадратные уравнения
Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:
ax 2 + bx + c = 0 — квадратное уравнение,
где x — это неизвестное, а a, b и c — коэффициенты уравнения. В квадратных уравнениях a называется первым коэффициентом (a ≠ 0), b называется вторым коэффициентом, а c называется известным или свободным членом.
называется полным квадратным уравнением. Если один из коэффициентов b или c равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.
Видео:Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать
Приведённое квадратное уравнение
Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на a, то есть на первый коэффициент:
| x 2 + | b | x + | c | = 0. |
| a | a |
Затем можно избавиться от дробных коэффициентов, обозначив их буквами p и q:
| если | b | = p, а | c | = q, |
| a | a |
то получится x 2 + px + q = 0.
Уравнение x 2 + px + q = 0 называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.
является приведённым, а уравнение:
можно заменить приведённым уравнением, разделив все его члены на -3:
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Решение квадратных уравнений
Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:
Для каждого вида уравнения есть своя формула нахождения корней:
| Вид уравнения | Формула корней | ||||
|---|---|---|---|---|---|
| ax 2 + bx + c = 0 |  | ||||
| ax 2 + 2kx + c = 0 |  | ||||
| x 2 + px + q = 0 |
|
Обратите внимание на уравнение:
это преобразованное уравнение ax 2 + bx + c = 0, в котором коэффициент b — четный, что позволяет его заменить на вид 2k. Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:
Пример 1. Решить уравнение:
Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:
Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:
| x1 = | -2 | = — | 1 | , x2 = | -12 | = -2 |
| 6 | 3 | 6 |
| Ответ: — | 1 | , -2. |
| 3 |
Определим, чему равны коэффициенты:
Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:
Приведём уравнение к общему виду:
Определим, чему равны коэффициенты:
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:
Определим, чему равны коэффициенты:
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:
Видео:ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать
8.2.2. Решение полных квадратных уравнений
I. ax 2 +bx+c=0 – квадратное уравнение общего вида
Дискриминант D=b 2 — 4ac.
Если D>0, то имеем два действительных корня:
Если D=0, то имеем единственный корень (или два равных корня) х=-b/(2a).
Если D 2 +5x-3=0.
Решение. a=2; b=5; c=-3.
D=b 2 — 4ac=5 2 -4∙2∙(-3)=25+24=49=7 2 >0; 2 действительных корня.
Пример 2) 4x 2 +21x+5=0.
Решение. a=4; b=21; c=5.
D=b 2 — 4ac=21 2 — 4∙4∙5=441-80=361=19 2 >0; 2 действительных корня.
II. ax 2 +bx+c=0 – квадратное уравнение частного вида при четном втором
коэффициенте b
Пример 3) 3x 2 -10x+3=0.
Решение. a=3; b=-10 ( четное число ); c=3.
Пример 4) 5x 2 -14x-3=0.
Решение. a=5; b= -14 ( четное число ); c=-3.
Пример 5) 71x 2 +144x+4=0.
Решение. a=71; b=144 ( четное число ); c=4.
Пример 6) 9x 2 -30x+25=0.
Решение. a=9; b=-30 ( четное число ); c=25.
III. ax 2 +bx+c=0 – квадратное уравнение частного вида при условии : a-b+c=0.
Первый корень всегда равен минус единице, а второй корень равен минус с, деленному на а:
Пример 7) 2x 2 +9x+7=0.
Решение. a=2; b=9; c=7. Проверим равенство: a-b+c=0. Получаем: 2-9+7=0.
Тогда x1=-1, x2=-c/a=-7/2=-3,5. Ответ: -1; -3,5.
IV. ax 2 +bx+c=0 – квадратное уравнение частного вида при условии: a+b+c=0.
Первый корень всегда равен единице, а второй корень равен с, деленному на а:
Пример 8 ) 2x 2 -9x+7=0.
Решение. a=2; b=-9; c=7. Проверим равенство: a+b+c=0. Получаем: 2-9+7=0.
Тогда x1=1, x2=c/a=7/2=3,5. Ответ: 1; 3,5.
🎬 Видео
Решение биквадратных уравнений. 8 класс.Скачать
Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать
ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ. §20 алгебра 8 классСкачать
Неполные квадратные уравнения. Алгебра, 8 классСкачать
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
Теорема Виета. 8 класс.Скачать
Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать
Тема: Квадратные уравнения. Урок: Уравнения вида y=ax^2 + bx +cСкачать
Решение уравнений вида |ax²+bx| +c=0 и ax²+b|x|+c=0Скачать
Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать
ТЕОРЕМА ВИЕТА // Как решать Квадратные Уравнения по АЛГЕБРЕ 8 классСкачать
Теорема Виета. Алгебра, 8 классСкачать
Математика| Разложение квадратного трехчлена на множители.Скачать
Решение квадратных уравнений (урок второй)Скачать
Алгебра 8 класс. Квадратные уравнения ах² + 2kx + c = 0 с чётным вторым коэффициентом.Скачать
