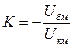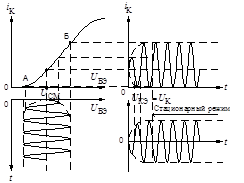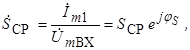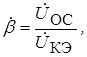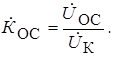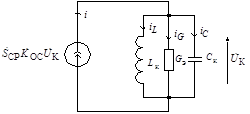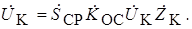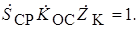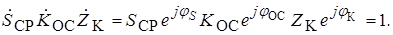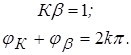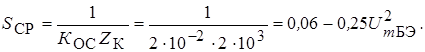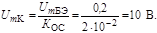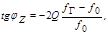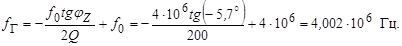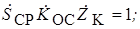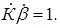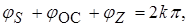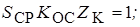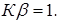Уравнение автогенератора и его решение (4 видео)

Автогенераторы. Основные уравнения АГ.

На рисунке 1.26 приведена упрощенная схема автогенератора (АГ) с трансформаторной обратной связью.

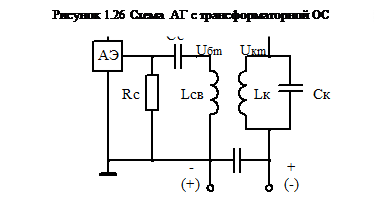Коэффициент передачи цепи ОС

Знак “ – “ указывает на то, что U_бм и U_км – противофазны.

Основное уравнение АГ можно записать в следующем виде:

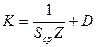
где S_ср – средняя крутизна характеристики 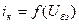АЭ, Z – сопротивление нагрузки, D – проницаемость АЭ.

Данное уравнение не имеет расчетного значения, так как величина 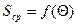– неизвестна (Q — угол отсечки).

Представим основное уравнение АГ в другом виде:

или

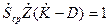
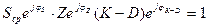
которое распадается на два уравнения, определяющие условия возбуждения:

– уравнение баланса амплитуд,

– уравнение баланса фаз.

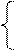
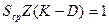
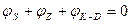
Одним из главных параметров АГ является стабильность частоты. Существует два способа стабилизации частоты:

1) Параметрический, куда относятся

— повышение добротности контуров,

— применение буферных каскадов,

— геометризация, экранирование и др.

2) Кварцевая стабилизация частоты, обеспечивающая относительную нестабильность .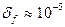

При применении обоих способов стабилизации частоты удается достичь .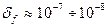

Нестабильности порядка 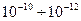достигаются применением квантовых стандартов частоты.

Дата добавления: 2016-02-04 ; просмотров: 4629 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Автогенератор. Баланс амплитуд и фаз. Условия самовозбужденияСкачать

Сущность квазилинейного метода анализа

УРАВНЕНИЕ САЦИОНАРНОГО РЕЖИМА АВТОГЕНЕРАТОРА И ЕГО АНАЛИЗ

Содержание

Анализ стационарного режима автогенератора

Графический анализ стационарного режима автогенератора

Введение

Теория и техника генерирования гармонических высокочастотных колебаний в нынешнем виде сложилась не сразу. Она подготовлена усилиями ученых и инженеров всех стран мира и прошла в своем развитии ряд этапов. Как уже отмечалось в лекциях по данной теме, на смену дуговым генераторам незатухающих высокочастотных колебаний пришла электромашинная высокочастотная техника, с которой неразрывно связано имя Валентина Петровича Вологдина. Его высокочастотные электромашинные генераторы являлись надежным источником радиоколебаний на начальном этапе развития радиотехники.

В. П. Вологдин родился в 1881 году в бывшей Пермской губернии в семье инженера горного дела. Окончил Петербургский технологический институт в 1907 году. Первая русская машина высокой частоты была построена В. П. Вологдиным в 1912 году. Мощность ее составляла 2 кВт при частоте 60 кГц. Машина отвечала всем требованиям времени и превосходила, по оценкам специалистов, иностранные разработки. После Октябрьской революции В. П. Вологдин возглавил в качестве одного из научных руководителей вновь созданную Нижегородскую радиолабораторию. Здесь под его руководством были построены электромашины на 50, а затем на 150 кВт. В 1925 году последняя была установлена на Октябрьской радиостанции в Москве и обеспечивала связь с городами Европы и Америки.

Под руководством В. П. Вологдина были созданы и первые ртутные выпрямители мощностью до 10 кВт при напряжении 3,5 кВ для питания ламповых радиопередатчиков, а также большая работа была проделана по разработке других выпрямительных устройств.

В 1939 году В. П. Вологдин был избран членом-корреспондентом Академии наук СССР, не раз удостаивался Государственных премий СССР. Он первым награжден Золотой медалью им. А. С. Попова.

В. П. Вологдин умер 23 апреля 1953 года. Его имя носит научно-исследовательский институт токов высокой частоты, в котором ему пришлось работать в последние годы жизни.

Анализ стационарного режима автогенератора.

Сущность квазилинейного метода анализа

Как радиотехническое устройство генератор используется в режиме стационарных колебаний с постоянными их параметрами (амплитудой и частотой). При исследовании стационарного режима работы основными задачами являются:

— определение условий возникновения режима стационарных колебаний;

— определение амплитуды и частоты стационарных колебаний;

— оценка устойчивости автоколебаний (стационарных режимов).

При выполнении условий самовозбуждения в генераторе возникают автоколебания, и их амплитуда непрерывно растет (рис. 1).

Рис. 1. Возникновение и стабилизация колебаний в автогенераторе

Затем усилительный элемент (транзистор) входит в нелинейный режим и его усилительные свойства, вследствие ограничения выходного тока, падают, рост амплитуды колебаний замедляется, а затем прекращается вовсе, тогда наступает стационарный режим.

Выходной ток в силу нелинейности рабочей области АБ является негармоническим, но периодическим, имеющим частоту колебаний, равную резонансной частоте контура. Напряжение на контуре, при достаточно высокой его добротности, создается только первой гармоникой тока и является гармоническим.

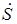
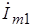
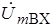
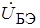
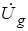
Таким образом, в стационарном режиме нелинейный усилительный элемент можно рассматривать по отношению к контуру как источник первой гармоники, который поддерживает автоколебания в контуре. Схема замещения генератора по переменному току в стационарном режиме имеет такой же вид, что и в режиме самовозбуждения, с той лишь разницей, что теперь вместо следует считать среднюю крутизну усилительного элемента по первой гармонике выходного тока

где – комплексная амплитуда первой гармоники выходного тока усилительного элемента;

– комплексная амплитуда управляющего напряжения, под которым понимается напряжение на входе усилительного прибора трехполюсного типа или напряжение на нелинейном элементе двухполюсного типа ( в генераторе с трансформаторной обратной связью или в генераторе на туннельном диоде).

Метод расчета генератора, основанный на представлении нелинейного усилительного элемента в виде линейного со средними по первой гармонике параметрами, разработан русским академиком Ю. Б. Кобзаревым в 30-е годы и получил название квазилинейного метода. Он находит самое широкое применение в инженерной практике.

В общем случае средняя крутизна 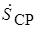является комплексной величиной. Одной из причин появления фазового сдвига j_S между выходным током и управляющим напряжением может быть конечное время пролета носителей заряда в усилительном элементе. Кроме того, сдвиг по фазе j_S может быть обусловлен самой формой ограниченного выходного тока, из состава которого выделяется первая гармоника.

При анализе стационарного режима генератора принято за коэффициент обратной связи считать не

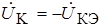
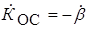
Так как , то и эквивалентную схему генератора с трансформаторной обратной связью представим, с учетом приведенных рассуждений, в следующем виде.

Рис. 2. Эквивалентная схема автогенератора в стационарном режиме

Из схемы видно, что

Из выражения получаем условие стационарного режима

Представим через модули и фазы средней крутизны S_СР и j_S, коэффициента обратной связи К_ОС и j_ОС и сопротивления контура Z_K и j_К:

Из данного выражения следуют два соотношения, определяющие стационарный режим:

(1)

(2)

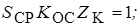
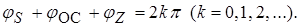
Уравнение (1) называют уравнением баланса амплитуд, а уравнение (2) – уравнением баланса фаз. Уравнение баланса амплитуд позволяет определить амплитуду колебаний в стационарном режиме работы автогенератора, а уравнение баланса фаз – частоту этих колебаний, так как хотя бы один из фазовых сдвигов зависит от частоты.

Для генераторов с внешней цепью обратной связи условия стационарности иногда используют в виде

Средняя крутизна имеет выражение S_СР = 0,06–0,25 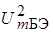мА/В. Определить амплитуду напряжений на базе и коллекторе транзистора, если К_ОС = 0,02 и Z_К = 2 кОм.

В работающем генераторе обязательно выполняется уравнение баланса амплитуд 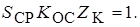Отсюда

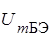
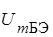
Решая это уравнение относительно , получим = 0,2 В. Далее нетрудно найти амплитуду напряжения на коллекторе транзистора

Фаза средней крутизны в автогенераторе j_S = 5,7°. Найти частоту генерируемых колебаний, если добротность колебательного контура Q = 100, резонансная частота колебательного контура ¦₀ = 4 МГц, фазовый сдвиг по цепи обратной связи j_ОС = 0.

В работающем генераторе обязательно выполняется уравнение баланса фаз 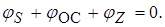Отсюда j_Z = — j_S. Для параллельного контура

1. Целью анализа стационарного режима является выявление условий наступления этого режима и определение амплитуды и частоты установившихся колебаний.

2. Выявление условий стационарности сводится к анализу нелинейной электрической цепи приближенными методами, среди которых широкое применение нашел квазилинейный метод анализа.

3. В квазилинейном методе анализа нелинейный элемент заменяется линейным со средними параметрами (в частности, средней крутизной) по отношению к первой гармонике выходного тока. Необходимым условием применения квазилинейного метода является высокая добротность контура.

4. Условия стационарности могут иметь различные формы записи, в зависимости от конкретной схемы автогенератора:

Эти условия записываются обычно в виде двух вещественных уравнений каждое, первое из которых называется уравнением баланса фаз, позволяющим определить частоту колебаний автогенератора, а второе – уравнением баланса амплитуд, позволяющим определить амплитуду колебаний в стационарном режиме:

5. В стационарном режиме энергия колебаний, вносимая активным прибором в контур, равна энергии потерь в нем (G_АП = G_Э). На резонансной частоте эквивалентная проводимость колебательного контура во много раз больше собственной проводимости активного прибора G_Э >> 1/R _i, поэтому можно полагать, что G_Э » 1/R_Э, а на резонансной частоте контура Z_К = R_Э0.

Видео:Автоэлектрик раскрыл все секреты работы генератора и его неисправности!!!Скачать

Дифференциальное уравнение автогенератора

Анализ работы автогенератора проводят на основе решения его дифференциального уравнения, но сначала рассмотрим свободные колебания в LС — контуре. Это необходимо сделать в связи с тем, что колебательный контур является главным элементом автогенератора гармонических колебаний, а источник постоянного тока, регулятор и цепь обратной связи — вспомогательными элементами, с помощью которых лишь компенсируются потери энергии в колебательном контуре. Для изучения физических процессов, происходящих в одиночном колебательном контуре, рассмотрим схему рис. 3, а

Рис. 3. Свободные колебания в LС — контуре:

а — принципиальная схема; б — временная диаграмма.

Сначала ключ K находится в положении 1 и в контуре происходит накопление энергии в виде заряда конденсатора С. Если в момент t = 0 перевести ключ K в положение 2, то в контуре возникнут свободные колебания, которые описываются дифференциальным уравнением

или после дифференцирования и деления на L

. (1)

Вводя обозначение , (δ — коэффициент затухания контура) и учитывая, что ,

последнее уравнение можно записать в окончательном виде:

. (2)

С учетом того, что в радиоэлектронике используются колебательные контуры с малыми потерями, решение дифференциального уравнения (2) будет иметь вид

, (3)

где I₀ — начальная амплитуда тока в колебательном контуре, зависящая от запасенной контуром энергии, а ω_CB ≈ ω_P — частота свободных колебаний.

Свободные колебания в контуре будут иметь форму, показанную на рис. 3, б. Очевидно, в обычном контуре свободные колебания будут затухающими из — за наличия потерь (сопротивление г).

Теперь перейдем к автогенератору. Но прежде чем составлять его дифференциальное уравнение, отметим, что в зависимости от условий работы автогенератора необходимо учитывать разное число параметров, характеризующих происходящие в нем процессы. Например, на низких частотах активный элемент автогенератора можно считать безынерционным и имеющим очень большое входное сопротивление, что приводит к простому дифференциальному уравнению. При увеличении генерируемой частоты следует учитывать величину входного сопротивления и инерционность активного элемента, что усложняет дифференциальное уравнение. Ограничимся простейшим случаем и составим дифференциальное уравнение для транзисторного автогенератора с трансформаторной связью (рис. 4), предполагая, что частота генерируемых колебаний. достаточно низка и можно не учитывать инерционные свойства транзистора и величину его входного сопротивления. Для этой схемы справедливы следующие уравнения:

Рис. 4. Принципиальная схема по переменному току транзисторного LС — автогенератора

(4)

Заменив во втором уравнении (4) ток в емкостной ветви контура через ток в индуктивной ветви и коллекторный ток: i_C(t) = i_K(t) — i(t) и продифференцировав полученное выражение по времени, получим дифференциальное уравнение автогенератора для токов:

(5)

Поскольку в рассматриваемой схеме автогенератора существует обратная связь, на базе транзистора возникает переменное напряжение и₆, которое является функцией тока в индуктивной ветви контура:

U_В(t) = ± M

Знак «±» обусловлен тем, что катушка обратной связи может быть включена либо согласно, либо встречно по отношению к контурной катушке L. Коллекторный ток i_к транзистора в общем случае является нелинейной функцией напряжений и_б и и_к. Однако во многих случаях в схеме рис. 4.4 транзистор работает в режиме, когда напряжение и_к мало влияет на ток i_к. Поэтому для упрощения можно пренебречь влиянием напряжения на коллекторе и считать, что коллекторный ток зависит только от напряжения на базе:

Тогда уравнение (5) принимает вид

(7)

или после преобразования правой части

M = M = M = Mφ((u_B(t)) . (8)

Подставляя в правую часть уравнения (7) выражение (8), проведя элементарные преобразования и опуская в дальнейшем индекс «б», получим основное уравнение автогенератора:

. (9)

Это нелинейное дифференциальное уравнение второго порядка, точного решения которого в настоящее время не существует. Поэтому в теории автогенераторов приходится пользоваться приближенными методами. При этом для исследования одних вопросов используют методы грубого приближения, для других — достаточно точные. Наиболее грубым приближением является линеаризация уравнения (4.9), которая применяется для определения условий самовозбуждения автогенератора. Более точным является квазилинейный метод, позволяющий решить задачу об амплитуде и частоте стационарных колебаний автогенератора. И, наконец, для ответа на вопрос о поведении автогенератора в любой момент времени приходится использовать наиболее точные методы решения нелинейных дифференциальных уравнений, например метод медленно меняющихся амплитуд (метод Ван – дер – Поля). Далее исследуются основные режимы работы автогенераторов.

1.2. Самовозбуждение автогенератора

При определении условий самовозбуждения интересуются лишь начальной стадией процесса, когда колебания в автогенераторе только что возникли, их амплитуды очень малы и лампу или транзистор (в принципе сугубо нелинейные элементы) можно рассматривать как линейные. Учитывая малость напряжений и то, что при этом используются очень небольшие участки вольт-амперных характеристик активных элементов, которые можно считать линейными, вместо уравнения (6) запишем

где S = — крутизна характеристики транзистора. Тогда правая часть уравнения (7) примет вид M = MS и уравнение (9) превратится в следующее линейное

. (11)

= 2δ_ЭКВ. (12)

.и учитывая, что , получим

. (13)

Это дифференциальное уравнение аналогично дифференциальному уравнению свободных колебаний простого колебательного контура (2). Поэтому общее решение уравнения (13) имеет тот же вид:

где U₀ — начальная амплитуда напряжения на колебательном контуре автогенератора.

Однако вместо величины δ в решение дифференциального уравнения автогенератора входит величина δ_ЭКВ, которая зависит не только от параметров колебательного контура l, С, г,

Рис. 5. Временные диаграммы напряжений в автогенераторе при различных значениях величины эквивалентного затухания колебательного контура

но и от параметров автогенератора — транзистора (5) и цепи обратной связи (М).Кроме того, если в колебательном контуре значение δ всегда положительно, то в автогенераторе в зависимости от его параметров величина δ_ЭКВ может быть как положительной, так и отрицательной. Это приводит к тому, что решение дифференциального уравнения автогенератора может существенно отличаться от решения дифференциального уравнения свободных колебаний простого колебательного контура. Выбрав такое направление наводимой э. д. с., чтобы можно получить в зависимости от пара метров автогенератора три значения δ_ЭКВ

соответствующие трем принципиально разным

δ_ЭКВ = ,

решениям уравнения (13): δ_ЭКВ > 0; δ_ЭКВ = 0; δ_ЭКВ 0 колебания в

автогенераторе будут затухающими. Если автогенератор вывести из состояния статического равновесия любым внешним воздействием, то через некоторое время колебания в нем прекратятся (рис. 5, а). Процессы в таком автогенераторе качественно совпадают со свободными колебаниями в простом колебательном контуре, отличаясь от них только меньшим коэффициентом затухания (δ_ЭКВ 0 самовозбуждение автогенератора невозможно. При δ_ЭКВ = 0 колебания в автогенераторе становятся незатухающими (рис. 5, б).

Случайно возникшие в автогенераторе колебания будут оставаться неизменными неопределенно долгое время. Однако и такой автогенератор не будет самовозбуждаться.

Наконец, при δ_ЭКВ ‘ =

причем для выполнения условия самовозбуждения энергия, вносимая в контур, должна превышать его энергию рассеяния (W ‘ ). Из рассмотрения схемы автогенератора можно показать, что I ‘ _K = I_KρSMω_P_. Тогда условие возбуждения запишется так: ρSMω_P> 1 или

Энергетическая трактовка процессов, происходящих при самовозбуждении автогенераторов, позволяет понять, как влияют параметры автогенератора на условия его самовозбуждения. Чем больше крутизна характеристики активного элемента и коэффициент обратной связи, — тем большее количество энергии поступает в колебательный контур и тем легче происходит самовозбуждение автогенератора. Аналогично чем больше добротность колебательного контура, тем меньше потери энергии и тем легче происходит самовозбуждение автогенератора.